处理双变量函数问题的五种方法
河南大学数学与统计学院 (475001) 卢 阳 张蒙蒙
在近年来的函数综合题中,常常出现两个在某个范围内都可以随意变化的量,即双变量函数问题.这类问题学生常常由于不知选择哪个自变量作为研究对象而导致思路无法继续.为此,本文归纳梳理解决这类问题的思想和方法,对同学们攻克函数综合问题将有所帮助.
一、变量归一,消元构造法
双变量问题含有两个变量,很自然的想法便是消去一个变量,变成一元函数问题.
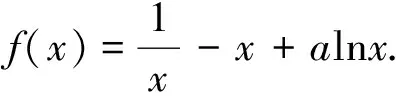
(1)讨论f(x)的单调性;
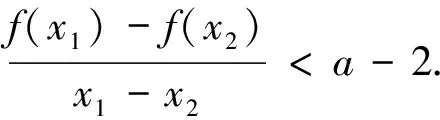

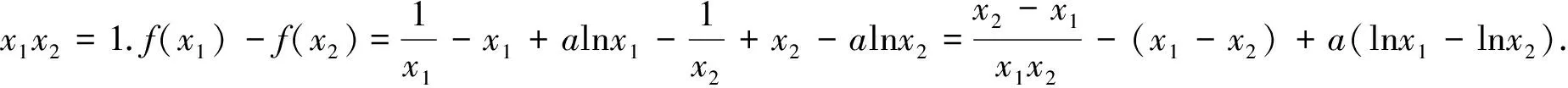
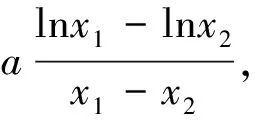
评注:该题两元之间存在关系,故可消去其中一个变量,变成一元函数解决,该类问题近几年经常出现,如2016年课标全国卷Ⅱ第21题做法和此题非常相似,难点在于找到各元之间的关系,读者可以对比归纳.

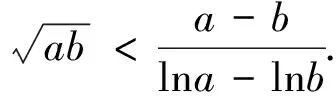
评注:由上证不等式可以很快得出例1的答案.对数平均不等式的证明方法具有代表意义,很多问题都需要把双变量所代表的运算式看成整体去进行消元.
例3 已知函数f(x)=aex+b在(0,f(0))处切线为x-y+1=0.
(1)求f(x)的解析式;
(2)设A(m,f(m)),B(n,f(n)),m 设h(t)=et-t-1,h′(t)=et-1>0,t>0.即h(t)在(0,+∞)上单调递增,所以h(t)>h(0)=0,故t 小结:例1、例2、例3都是通过消元去解决问题.不同的是,例1根据题目条件可以直接消去其中一个变量;例2,例3需要创造条件,把双变量看成一个整体,我们称为“变量归一”思想. 例3的方法带有一定技巧性,有些学生不易想到,观察到两变量之间是相互独立的,可以“矮子里面挑将军”,选择其中一个变量当成主变量,视其他变量为参数进行讨论. 对例3再采用“指定主元法”进行解决,把n当成主元,把m当成参数. 分析:a,b地位一样,直接操作,不知“力往何处使”.不妨将a当成主元,着重使力. 解:先证右边,即证alna-blnb>(a-b)(lnb+1).以a为主元,设h(a)=alna-(lnb+1)a-blnb+blnb+b,a∈(0,b).即h(a)=alna-(lnb+1)a+b,h′(a)=lna-lnb<0.所以h(a)在(0,b)上单调递减,则h(a)>h(b)=0.所以当a∈(0,b)时,alna-blnb>(a-b)(lnb+1).左边同理可证. 小结:指定主元法在双变量问题中经常使用,前提是两个变量之间“无牵无挂”.如例2也可以用指定主元法解决,有兴趣的读者可以试做.但若两变量之间有联系,如例1,那么便不能指定其中一个变量为主元进行讨论. 双变量问题中含有两个变量,有时按照常规思维对两个变量进行区分主次,往往会陷入困境.此时若变换主元,反客为主,会有柳暗花明的感觉. 例5 (2017天津预赛题)实数a,b满足|a|≤1,|a+b|≤1,求(a+1)(b+1)的取值范围. 分析:此题a,b关系不好直接表达出来.若设t=a+b,则可将b消去. 评注:此题若把a看成主元,则是关于a的二次函数,需要对对称轴的位置进行讨论.转变视角之后变成关于t的一次函数,则简化此题. 小结:从上述两例可以看出若主元选择得当,将会降低思维难度,简化解题过程,主元变换最大的好处就是把复杂函数变成简单函数.另外,主元变换蕴含着转化与化归思想,体现了和谐统一,普遍联系的哲学观点,使用得当,往往会使我们另眼看题. 双变量问题多为不等式问题,而不等式的证明常常需要利用函数单调性来处理.因此,单调性构造法显得尤为重要. 例7 已知函数f(x)=(x-1)ex+ax2有两个零点.(1)求a的取值范围;(2)设x1,x2是f(x)的两个零点,证明x1+x2<0. 分析:第(1)小题一般采用单调性的讨论来判断零点个数,答案也是这么给出的.但如果利用函数与方程思想将零点问题变成两函数交点问题便能化繁为简;第(2)小题是极值点偏移问题,需要将两变量变到同一单调区间,再利用单调性证明. 解:(1)见分析,a>0.(2)不妨设x1 评注:极值点偏移问题从2009年开始出现,到2016年再一次出现在全国卷上,属于难题.最主要的难点在于需要将x1,x2变到同一单调区间,再联系单调性进行证明.在证明过程中,还有一个难点在于如何将x1,x2和a三个变量进行消元变成一个变量,这里需要用到方法一的“变量归一,消元构造法.” (1)求f(x)的单调区间; (2)存在x1,x2∈(1,+∞)且x1≠x2,使 |f(x1)-f(x2)|≥k|lnx1-lnx2|成立,求k的取值范围. 小结:以上两例都是通过等价转化为函数单调性问题加以解决.另外,例8也可以用指定主元法解决.读者可以尝试. 分析:题意实际上是想说明无论f(x1)怎么取值,都有g(x2)比它大,也即f(x)max≤g(x)max. 评注:实际教学中很多学生对“任意、存在”问题难以理解,笔者将这类问题形象的表示为“孙悟空与如来佛”的故事.如例9,把f(x)看成孙悟空,把g(x)看成如来佛,题目可以表示为“无论孙悟空在M时期法术有多强,在N时期都存在某种状态的如来佛可以击败他”,即M时期孙悟空法术最大值≤N时期的如来佛法术最大值,也即f(x)max≤ g(x)max. 总结:函数题中的双变量问题是近年来高考中的“宠儿”,题型多样,方法多变,对思维能力和运算能力要求较高.在学习这类问题时需要通过练习熟悉题型,更重要的是领悟每种方法背后的思想,从而进行归纳整理.笔者给出处理这类问题的五种常见方法与其中蕴含的数学思想,旨在抛砖引玉,希望引起读者思考.
二、委以重任,指定主元法
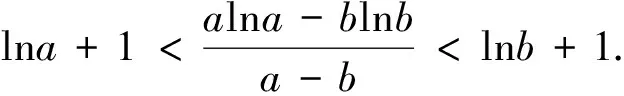
三、反客为主,变换主元法
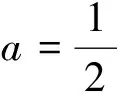
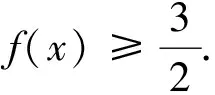
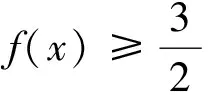
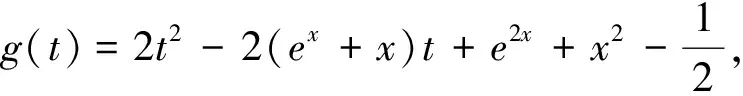
四、利用性质,单调性构造法

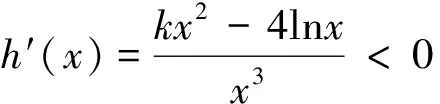
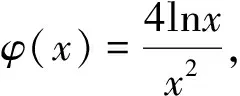
五、理清题意,转化为最值问题法