多原子反应体系的高精度拟合势能面

傅碧娜，陈 俊，刘天辉，邵科杰，张东辉

中国科学院大连化学物理研究所，分子反应动力学国家重点实验室，理论与计算化学研究中心，辽宁 大连 116023

1 引言

化学反应基本上是一个旧化学键断裂，新化学键形成的过程。从最基本和微观水平研究化学反应已经成为现代物理化学的重要目标。分子反应动力学是在原子、分子层次上研究化学反应微观动态和机理的一门学科，它所研究的基元化学反应能够解释量子态分辨的反应碰撞过程，并提供重要的反应机理信息。随着高灵敏性，高分辨率实验技术和动力学理论研究的发展和应用，反应动力学领域取得了许多有重要意义的成果，并且已经从一些研究很彻底的三原子反应过渡到真正的多原子反应1–30。

多原子反应动力学理论研究在两个方面受到了很大的挑战，一是势能面，二是动力学。在Born-Oppenheimer近似下，我们首先通过分离电子的运动和原子核的运动，采用从头算得到不同原子核构型下的势能值，根据这些分立的势能值构造反应的势能面；然后在构造好的势能面上求解核运动Schrödinger方程，就能得到反应的动力学信息，如反应几率，微分和积分反应截面，以及反应速率常数等，这个过程也就是我们常说的动力学计算。由此可见，构造一个精确可靠的势能面对于反应动力学的理论研究是头等重要的，它是我们正确理解一个化学反应机理的前提。

近几十年来，随着电子结构理论和从头算数据拟合技术的发展，使得精确的多维全域势能面的构造成为可能31–40。构造一个精确的势能面需要大量的高精度从头算，这些从头算能量点分布在一个很大的构型空间，另外需要一个可信的函数形式来表征这些分立的能量点。由于计算机能力的不断提升，高精度从头算理论比如耦合簇(CC)41或者多参考组态相互作用(MRCI)42方法，结合较大的基组，基本上可以给出可靠的从头算能量。然而，基于这些分立的能量点，如何构造多维分子体系可靠的全域势能面还是一个很大的挑战。

样条插值方法以及基于多体展开和函数形式的非线性拟合方法在三原子体系中运用是相当成功的43,44。对于四原子以上的反应体系，体系自由度的迅速增加使得如何能精确有效地构造多原子反应势能面成为了动力学领域的关键问题和难点。如果按每个自由度分布固定数据点的方法来做样条插值，就需要非常大的从头算计算量，这对目前的计算机水平是无法实现的。移动插值最小二乘法(IMLS)31和改进的Shepard插值方法32是典型的插值方法，用来构造多原子分子体系势能面。我们组曾经用改进的Shepard插值方法构造了CH5和 OH3体系全维势能面23,45。这些插值势能面的缺点是计算量很大，很大程度上限制了动力学势能值计算的速度。Bowman等人发展了置换不变多项式(PIP)拟合方法33,34，在构造高维势能面的工作上前进了重要的一步。置换不变多项式拟合方法使用首要不变量(首要多项式)和次要不变量(次要多项式)作为基函数，生成所需的置换不变多项式，最后通过线性最小二乘法获得各个多项式的系数。这个方法所用到的多项式基组考虑了体系的置换不变对称性，是一种有效的复杂多原子反应体系的全维势能面构造方法，并被成功应用于一系列复杂体系的势能面构建46,47。

近几年，神经网络(NN)方法48被广泛应用到多原子分子体系的高精度势能面构建中。神经网络的函数形式非常灵活，因此原理上可以利用NN拟合任意一种函数形式，而且拟合精度也能很高。在过去的二十年，神经网络方法在气相分子与金属表面反应以及气相体系势能面的构建中有不少研究49–55。然而，怎样系统地选择新的构型用来从头算，进而开展有效的势能面拟合以及动力学计算，最后得到可靠的动力学结果，一直以来是困难的工作。近几年，我们组完善和发展了一套系统的方案用于有效地选择构型36,37,56，根据此方案，可以流程化地选择足够多且广泛分布在势能面重要区域的数据点集。最后能让神经网络拟合得到的势能面精度达到量子动力学的需求，并且得到可靠的量子动力学结果。接着，Guo等人提出了PIPNN方法38,39，他们不再使用分子的核间距作为神经网络的输入层，而是采用 Bowman等提出的置换不变多项式，作为神经网络的输入层。PIP-NN拟合方法将相同原子的置换对称性严格考虑到神经网络方法拟合中。这个方法理论上要求所使用的多项式包含所有的首要不变量和次要不变量。但随着体系的增大，输入层多项式的个数随次要不变量的最高次数呈非线性增长。

神经网络是一个较为理想的通用型拟合方法，若能在保证对称性的前提下有效减少神经网络输入层多项式的个数，那么神经网络就有可能用于更为复杂的体系的势能面构建上。为此，我们组最近提出了基本不变量神经网络(FI-NN)拟合方法40。FI-NN使用基本不变量作为神经网络的输入，在保证势能面的对称性的同时能有效提高势能面的计算速度。在PIP及PIP-NN方法中，由于多项式的数目增长迅速，很多情况下两者需要使用按次数截断的多项式。对于较小的分子体系，使用PIP和PIP-NN方法拟合势能面时，通过选择合适的截断次数，可以得到较好的拟合结果，并同时确保所使用的多项式数目不至于过多。但当分子体系增大时，只能选择较低阶的多项式，这会使势能面的拟合结果达不到理想水平。同时，舍弃高阶多项式意味着拟合时所使用的生成元不完备，这也将导致额外误差的引入。为了减少神经网络输入层多项式的数目，并同时保证生成元的完备性，我们可以使用基本不变量作为神经网络的输入，这就是基本不变量神经网络。理论上，通过增加隐藏层神经元的个数，神经网络可以用于拟合任意形式的函数。又由于基本不变量是完备的生成元，所以基本不变量神经网络可以用于拟合任意形式的具有交换不变性的势能面。总体来说，FINN方法在数学形式上是精确而简洁的，同时由于输入层限制的减少，其神经网络结构也更为合理。

本文主要介绍我们组在近几年基于神经网络方法的势能面构造的进展。首先简单介绍基于神经网络的势能面构造方法，然后详细讨论这些方法在气相多原子反应，以及气相分子在金属表面反应的应用。这些反应体系包括OH3，HOCO，CH5气相反应体系，以及 H2O在 Cu(111)表面的解离等。

2 神经网络(NN)

前馈型神经网络是一种较为简单的神经网络函数，也是常用于化学反应势能面构造的类型。我们组都是采用前馈型神经网络进行势能面拟合。图 1(a)是具有两个隐藏层的前馈型神经网络函数的结构示意图，图中的每一个圆形节点称为一个神经元。如果输入层(input layer)、第1隐藏层(1st hidden layer)、第2隐藏层(2nd hidden layer)、输出层(output layer)的神经元数目分别为I、J、K、L，那么这个神经网络的结构为I-J-K-L。图1(b)是其中一个神经元的运算规则。对于第m层的第i个神经元，它有对应的输入值，输出值，以及激发函数fm。如图1所示，神经网络第1隐藏层的输入与输出分别为：

神经网络第2隐藏层的输入与输出分别为：

神经网络最终的输出层为：

图1 (a) 具有两个隐藏层的前馈型神经网络函数结构示意图；(b) 隐藏层中神经元的运算规则Fig.1 (a) Illustration of the functional structure of a feed forward neural networks;(b) the computing rule of a neuron in the hidden layer.

当神经网络应用到分子反应势能面的拟合时，神经网络的输入层对应分子构型的坐标，一般采用分子的内坐标或者原子核间距来表示，也可以使用精心构造的对称化坐标。在拟合的过程中，我们会对隐藏层选取不同的神经元个数来进行尝试拟合得到一个好的神经网络结构，因为神经网络结构对于拟合的好坏有很重要的影响。对于一个确定好的神经网络结构，我们可以通过Levenberg-Marquardt运算法则57对公式(1)–(5)中的权重和偏差进行调整，我们用均方根偏差(RMSE)来确定神经网络拟合的好坏，

我们在拟合过程中不断地优化参数，使误差RMSE减小到足够的精度。当输出的RMSE小于预先设定的阈值，或者RMSE的下降速率小于一定的标准，意味着拟合结束，我们就用神经网络得到了一个NN势能面。值得指出的是，设定不同的随机值神经网络会得到不同的拟合结果，这是因为神经网络拟合是通过寻找局域拟合误差最优的过程。在神经网络结构确定的情况下，我们一般也会进行多次拟合，最后取RMSE最小的一次或几次拟合结果作为最终的势能面。

Levenberg-Marquardt运算法则在神经网络拟合中是通过迭代来实现的，它的计算量和计算时间随着要拟合的点的数目和我们所选取的神经网络结构中神经元的数目的增加而快速上升。为了加快神经网络拟合的速度，我们一般采用对总的能量点分块的方法(一般根据能量点构型所处的位置如入口区，相互作用区，出口区等)，对这些部分分别进行训练和测试来得到比较好的拟合，最后再把它们连在一起构成一个全域的势能面。这样处理能够减少神经网络结构中神经元的数目而减少计算量和拟合所需要的时间，而且能使我们方便地对各部分拟合得到比较理想的RMSE，特别是对动力学反应比较重要的区域如入口区和相互作用区，我们可以投入更多的时间和精力来把它们拟合得更好。

选择合适的构型用于从头算是势能面构造的关键，完备的构型集合需要覆盖反应涉及到的所有区域，并且在过渡态等重要区域包括更多的构型。我们发展和完善了一套系统的构型选择方案，通过多次添加构型和拟合，最终得到可靠的势能面，从而计算出可靠的反应动力学结果。我们一般通过低精度的从头算动力学方法计算某些轨线，去搜索所有可能的反应通道和分子能够到达的构型空间。并将这些轨线上的构型经过筛选(基于每两个核构型间的距离)，得到第一批构型的集合。然后使用高精度从头算方法计算这些构型的能量，再使用NN方法进行多次拟合，得到了最初版本的势能面。得到最初版本的势能面以后，就能很快开展大量的准经典轨线计算，在轨线经历的这些构型中筛选新的构型加入原来的从头算数据集，进行之后势能面的改进。我们需要从各个通道和不同的过渡态区域出发进行经典轨线计算，目的是让势能面能精确地描述每一个反应通道。这样经过若干次重复之后，就可以进行量子动力学计算，判断势能面是否收敛。

最终拟合得到的势能面必须包括以下两方面才是可靠的，一是拟合误差RMSE足够小，在多次拟合的势能面上能计算得到一样的动力学结果；二是用于拟合的从头算构型数目足够多，并且覆盖范围足够广，再继续增加或者删除从头算构型重新拟合也能得到同样的动力学结果。当以上两个要求都满足时，表明势能面的构造过程已经完全收敛，基于此势能面能够得到可靠的动力学结果。

2.1 OH3体系

H2+ OH ↔ H2O + H反应是典型的四原子体系，它在大气化学和燃烧化学中占有重要的位置58,59。由于OH3体系中有3个原子是H，从头算或量子动力学计算量都相对比较小，所以是从头算势能面构造和量子动力学计算的典型代表。在过去几十年，人们用不同方法构造了WDSE60，OC61,62，WSLFH63，YZCL264，XXZ23等该体系的势能面。这些势能面要么不够精确，要么运算速度太慢。

因此，2013年，我们组使用神经网络方法，结合上述系统的构型选择方案，构造了一个全新的从头算势能面(CXZ势能面)36。CXZ势能面的构造将XXZ势能面已有的8000多个构型作为初始拟合数据集，采用UCCSD(T)-F12a/aug-ccpVTZ从头算方法计算势能，用多次神经网络拟合与准经典轨线计算相结合的方法来筛选构型，最终选择了 16814个构型作为拟合数据集。在进行拟合的时候，我们按照H原子与O原子的距离对3个H 原子进行排序，使得 ROH1≤ ROH2≤ ROH3，以此来保证一个构型在NN势能面上能量的唯一性。

为了提高拟合效率，我们将整个势能面分为三个区域，即(I) H2+ OH通道，(II) H + H2O通道，(III) OH3相互作用区，如图 2中的红色分割线所示。在分别对三个区域拟合时，为了保证连接处吻合程度，在连接处附近有一小部分构型同时用于两边的区域拟合。整体势能面则是用光滑的开关函数将这 3个单独的拟合连接，是它们的权重之和，记为 NN1 (即 CXZ势能面)，整体拟合误差RMSE为1.61 meV。另外,我们也将所有16814个从头算点同时用于一次拟合，采用6-50-80-1的神经网络结构得到了一个全域的势能面，记为NN2。NN2势能面的拟合误差RMSE为1.50 meV。为了测试从头算构型是否足够多，我们随机选择了16814个构型中 80%的数据，即使用 13451个构型，也按照整体拟合的方式构建了NN3势能面。NN1、NN2和NN3这三个势能面对所有数据的拟合误差随势能的分布如图3所示。

我们利用量子动力学方法来测试势能面构造的收敛性质。基于这3个NN势能面，我们使用全维量子波包方法计算了OH + H2→ H2O + H反应几率，以及交换反应H + HOH → H’ + HOH的反应几率，其中反应物都处于振转基态，分别如图4和5所示。可以看出，对于这两个反应通道,基于分区域拟合的 NN1势能面和整体拟合的 NN2势能面的量子动力学结果基本没有差别，而且，采用80%的数据点拟合出来的NN3势能面可以得到与NN1势能面基本一致的动力学结果。这些结果表明我们得到的势能面对拟合的数据点和拟合过程都能很好地收敛。基于这样的势能面，我们最终能得到可靠的动力学结果。

图2 所有用于从头算构型在O-H2和O-H3坐标空间上的分布，并以红色分割线将整体区域分成OH + H2，H + H2O和OH3相互作用区这三个部分36Fig.2 The spacial distribution of ab initio data points as a function of O-H2 and O-H3,with the red dividing lines for the OH + H2,H + H2O,and OH3 interaction parts 36.

图3 在NN1，NN2和NN3势能面上所有构型的拟合误差随着相对于OH + H2平衡构型的从头算能量的分布36Fig.3 The fitting errors for all the data points in NN1,NN2 and NN3 PESs,as a function of their corresponding ab initio energies with respect to OH + H2 36.

值得一提的是，CXZ(NN1)势能面的计算速度比XXZ势能面快挺多，并且要比XXZ势能面光滑，因此它代表目前OH3反应体系最精确的基态势能面。进一步的研究证明，基于CXZ势能面的量子动力学计算结果能与交叉分子束实验结果高度吻合。我们的势能面能够满足高精度实验和理论研究的需求。

图4 用六维含时波包法在NN1、NN2和NN3势能面上，在体系的总角动量Jtot = 0时计算得到的H2 + OH → H2O + H的反应几率36Fig.4 Reaction probabilities of H2 + OH → H2O + H from six-dimensional time dependent wave packet calculations on NN1,NN2 and NN3 PESs at the total angular momentum Jtot = 0 36.

图5 用六维含时波包法在NN1、NN2和NN3势能面上，在体系的总角动量Jtot = 0时计算得到的H2O + H →H2O + H′的反应几率36Fig.5 Reaction probabilities of H2O + H → H2O + H′from six-dimensional time dependent wave packet calculations on NN1,NN2 and NN3 PESs at the total angular momentum Jtot = 0 36.

2.2 HOCO体系

OH + CO → H + CO2反应在大气化学和燃烧化学中都扮演着重要的角色65,66。它与OH + H2直接反应不同，是一个典型的在反应路径上存在长寿命中间体的复杂反应。该反应过程中存在较稳定的HOCO顺式和反式结构，并且入口(OH + CO)与出口(H + CO2)通道都存在明显的势垒。由于HOCO体系包含3个非氢原子，并且反应途径上存在长寿命的中间体，使得这个体系的势能面构造和量子动力学计算都非常困难。

早期的一些势能面都不能可靠完整地描述这个体系67–71。2012 年，Li与 Guo 等使用 UCCSD(T)-F12b/aug-cc-pVTZ方法计算了大约35000个从头算能量点，通过置换不变多项式(PIP)拟合的方法构造了HOCO体系的全域势能面(CCSD-1/d和改进的CCSD-2/d势能面)72。这两个PIP势能面比以前的势能面要更加可靠，并且被用来做一些动力学计算。2013年，我们基于大约 70000个UCCSD(T)-F12b/aug-cc-pVTZ能量点，用神经网络方法构造了一个拟合精度更高的势能面37。这个HOCO NN势能面的构建过程跟上述的OH3体系相似。

我们首先在早期的 LTSH势能面上开展了少量的准经典轨线计算，通过判断距离的方式选择了第一批6000个数据点，进行高精度的从头算。从这些构型出发，通过多次 NN拟合和准经典轨线计算的方式来产生新的构型，构型筛选过程使用了与OH3体系相同的方案。基于NN势能面进行了大量的量子动力学计算来判断势能面的拟合过程是否收敛。最终的 NN势能面一共使用了～74400个从头算构型。

为了减少NN拟合计算量，提高拟合精度，我们又采用了 OH3体系中使用的分区域拟合的方案，将全域势能面分为HO + CO入口区域，HOCO相互作用区域，以及H + CO2出口区域，并对这三个区域分别拟合，分别测试收敛性。同时，为了提高低能量区域的精确性，在使用 Levenberg-Marquardt算法进行NN拟合的过程中，我们将高能部分适当减少权重，以保证低能部分更加精确。由于相互作用区的势能面形状非常复杂，我们使用多个势能面作平均的方式进一步降低拟合误差。最终的势能面在整体的能量范围内，拟合误差RMSE为9.2 meV。

我们用量子动力学计算了基于两个平均势能面以及去掉10%从头算点后拟合的势能面，HO +CO → H + CO2反应的总反应几率，如图6所示。从图中比较发现，反应几率基本相似，从而说明势能面相对拟合数据点和拟合方法都收敛得比较好。

相对于以前的势能面，NN势能面不仅使用了更大量的从头算数据，而且覆盖了所有的反应通道，在每个反应通道上的拟合精度都相当高，是HOCO体系最为可靠的势能面。

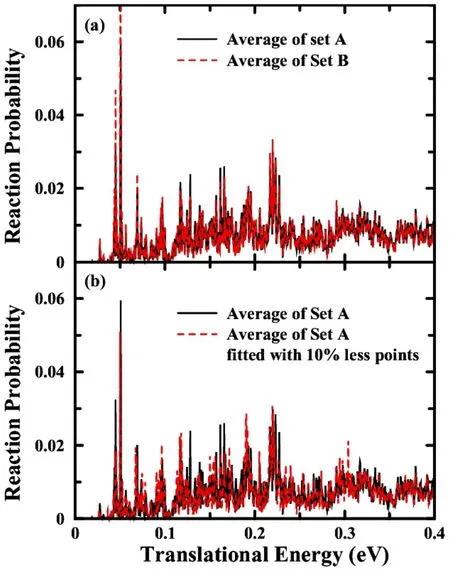
图6 (a) OH + CO → H + CO2 反应在2套势能面上的反应几率比较；(b) 在其中一套势能面上的反应几率和去掉10%从头算点重新拟合的势能面上计算得到的反应几率37Fig.6 (a) Comparison of total reaction probabilities for OH + CO → H + CO2 on two sets of PESs averaged over three fittings and (b) comparison of total reaction probabilities on one of the sets shown in (a) and a PES averaged over three fitting based on 10% less data points 37.

2.3 CH5体系

H + CH4→ H2+ CH3以及其逆反应在甲烷燃烧过程中非常重要57。作为 6原子体系反应的代表，人们对这个体系的研究已有很长的历史，这些研究大大提高了我们对多原子反应的认识。因为这个反应的6个原子中有5个H原子，所以成为很好的测试势能面和各种动力学方法的典型。

科学家们为了构建这个体系的精确势能面做出了巨大的努力。然而早期的半经典势能面都不能定量描述该反应73,74。2004年，Manthe等基于CCSD(T)从头算能量，采用改进的Shepard插值方法构造了第一个比较可靠的势能面75，并且用该势能面精确地计算了反应的速率常数。但是这个势能面是个局域的势能面，主要限制在过渡态区域，不能被应用于详细的全域动力学计算。Bowman等利用置换不变多项式方法，基于RCCSD(T)/augcc-pVTZ水平的高精度从头算数据，构建了ZBB1、ZBB2和ZBB376,77等一系列全域势能面。这些势能面包括了抽取和交换反应通道，比之前的势能面都更加精确。我们利用改进的Shepard插值方法，基于UCCSD(T)/aug-cc-pVTZ水平的从头算数据，构造了全维的 ZFWCZ 势能面45。测试表明，ZFWCZ 势能面精确度 ZBB3 势能面差不多，并且基于这两个势能面的量子动力学结果也基本一致。ZFWCZ势能面作为高维插值型的势能面，其计算速度比较慢，很难应用于进一步的动力学研究。

2014年，我们使用神经网络拟合方法，基于UCCSD(T)-F12a/aug-cc-pVTZ的从头算数据，构造了一个精确的势能面。这个势能面称为XCZ势能面54。XCZ势能面的构造采用ZFWCZ势能面和ZBB3势能面用到的50000多个构型，进而采用构型之间的欧氏距离进行筛选，保留了约8000个构型用于初始数据集。坐标采用15个键长作为神经网络的输入层，并且将5个H原子排序使得C―H键长呈递增关系。为了提高拟合和构型选择的效率,将整个势能面分为如图7所示的H + CH4渐近区(asymptotic region)、H2+ CH3渐近区(asymptotic region)以及 CH5相互作用区(interaction region)。与OH3体系类似，我们循环地增加新构型，并进行量子动力学结果测试。最终在全部的空间内一共选择了47783个构型，它们的空间分布如图7所示，这些构型同时覆盖了抽取和交换反应通道。

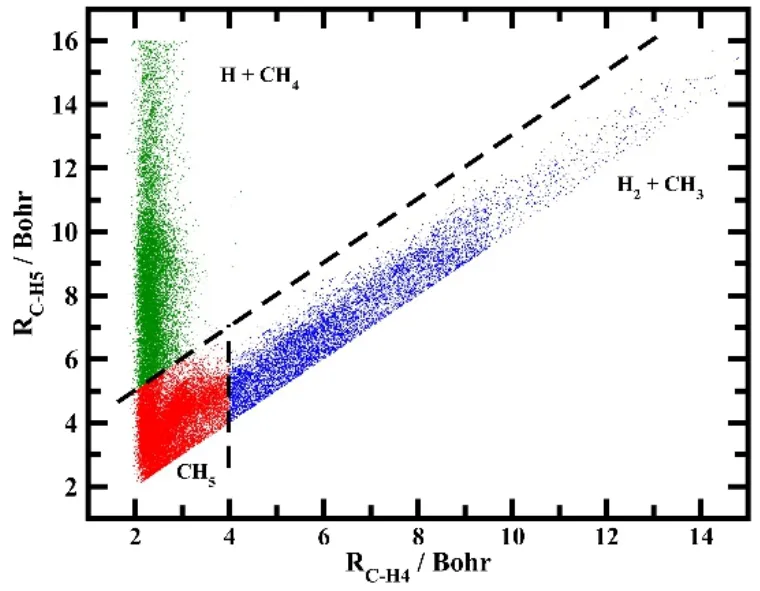
图7 H + CH4势能面的从头算点空间分布，其中H +CH4，H2 + CH3和CH5相互作用区分别由分割线隔开56Fig.7 The spacial distribution of ab initio data points as a funcion of RC-H4 and RC-H5,with the dividing lines for the H + CH4,H2 + CH3,and CH5 interaction parts 56.

为了进一步降低拟合误差，我们使用Agrafiotis曾提出的神经网络集合的方式78，将若干次拟合的势能面取平均从而减小随机误差。我们取RMSE最小的5次拟合的平均，作为此反应体系的最终版本神经网络势能面XCZ。最后，我们为了测试从头算构型的数目是否足够,只选择了所有构型中 90%的数据，拟合得到了另一个势能面。这个势能面与XCZ势能面的量子动力学结果如图 8所示，两者基本没有差异，表明势能面已经收敛得很好。

图8 基于所有从头算点拟合的NN势能面和基于90%从头算点拟合的势能面，H + CH4 → H2 + CH3的总反应几率比较56Fig.8 The reaction probabilities for the H + CH4 →H2 + CH3 reaction on the NN PES and another NN PES fitted with 90% of all data points 56.

2.4 H2O + Cu(111)体系

气相分子在过渡态金属表面的解离吸附在异相催化反应中起着非常重要的作用，是很多化学反应的决速步骤79。但是由于在构建势能面和发展新的理论方法存在很多困难，只能在非常少的体系上面开展量子动力学计算80,81。水在过渡态金属表面的解离吸附是蒸汽重整和水煤气转化过程中的重要一步82。基于刚性表面近似，H2O在金属表面的解离总共需要考虑 9个自由度。这对构建全维势能面和开展全维量子动力学计算是很大的挑战。

我们基于大量的DFT能量点，采用神经网络方法首次构建了H2O + Cu(111)体系拟合精度很高的全维(9维)势能面83,84。我们总共计算了 81102个DFT能量点，采用基于赝势和平面波的VASP软件包(Vienna ab initio simulation package)。DFT计算中采用广义梯度近似(GGA)下的 PW91泛函形式来描述交换相关能。

由于Cu(111)表面具有C3v对称性，我们只需要计算由top、fcc、hcp位构成的最小不可约三角形内的构型的能量值，三角形外面的构型的拟合的更好能量可以通过三角形内部的构型对称得到。我们只拟合三角形内部的数据点，考虑到特殊位置如top、bridge、fcc、hcp位置拟合的精确性以及边界的连续性，我们特意在这四个位置以及三角形的边界线上多选取了一些能量点，同时为了把边界拟合得更好，我们把三角形边界外部非常靠近边界的一部分能量点也包含进来，这部分能量点的能量不需要重新计算，只需要按对称性从三角形内部对称出来就行。这样拟合总共包含了93908个数据点，采用H2O分子的9个笛卡尔坐标作为神经网络拟合的输入层。

为了提高神经网络拟合的速度，我们把全部的数据点分成四个部分：渐进区(I)、相互作用区(II + III)和产物区(IV)，每个部分都有重叠。这样分块以后，每部分的能量点相比总的能量点以及需要的神经元数目大为减少，在不损失拟合精度的条件下加快了拟合的进度。对于每一部分，我们一般都要拟合几十次。为了测试这四个部分拟合的收敛性，我们每一部分选取三个RMSE比较小的拟合，它们一般是神经网络拟合的结构不同或者结构相同的时候，权重和偏差不一样。这十二个拟合可以组成81个势能面，我们把a1 + b1 + c1 +d1标示成NN1势能面，它的I，II，III，IV四部分的神经网络结构分别是9-80-75-1，9-80-75-1，9-80-75-1和9-85-70-1，RMSE分别是3.2 meV，10.1 meV,9.8 meV 和 13.1 meV。NN1 势能面总的RMSE 为9.0 meV，对于对动力学研究比较重要的部分(能量小于2.0 eV)RMSE 只有6.0 meV。我们又从剩下的80个势能面中随机选取了三个，用7维含时波包法分别计算了top位和bridge位基于这三个势能面和 NN1势能面的基态反应几率，如图9所示，可以看到，随着碰撞能的增加，反应几率是上升的，而且这三个势能面的反应几率和NN1势能面的反应几率基本上是重合的，也就是说NN1势能面对于神经网络拟合的过程是收敛的。

图10显示的是H2O的质心处于TS、Top、Bridge、Hcp位时的NN1势能面等高线图。可以看出，在这三个位置得到的L形状的反应路径是非常光滑的，并且从势垒的位置说明 H2O在Cu(111)解离是一个晚期势垒体系，意味着振动激发比平动能的增加对于反应会有更大的促进作用。我们在这个高精度拟合的全维全域势能面上成功在全维(9维)水平计算了H2O在Cu(111)表面的解离吸附几率，从而首次实现了一个三原子分子在固体表面反应的全维量子动力学研究，证明以前的减维模型会给计算带来较大的误差，代表着分子-表面量子散射动力学研究的一个重要突破82。

图9 H2O处于振转基态时，在top位和bridge位的7维解离几率，其中四个势能面从总共的81个势能面随机挑选产生83Fig.9 The seven-dimensional dissociation probabilities for H2O initially in the ground rovibrational state at fixed top and bridge sites calculated on four PESs we selected randomly from the total of 81 PESs (a,b,c,and d denote part I,II,III,and IV,respectively) 83.

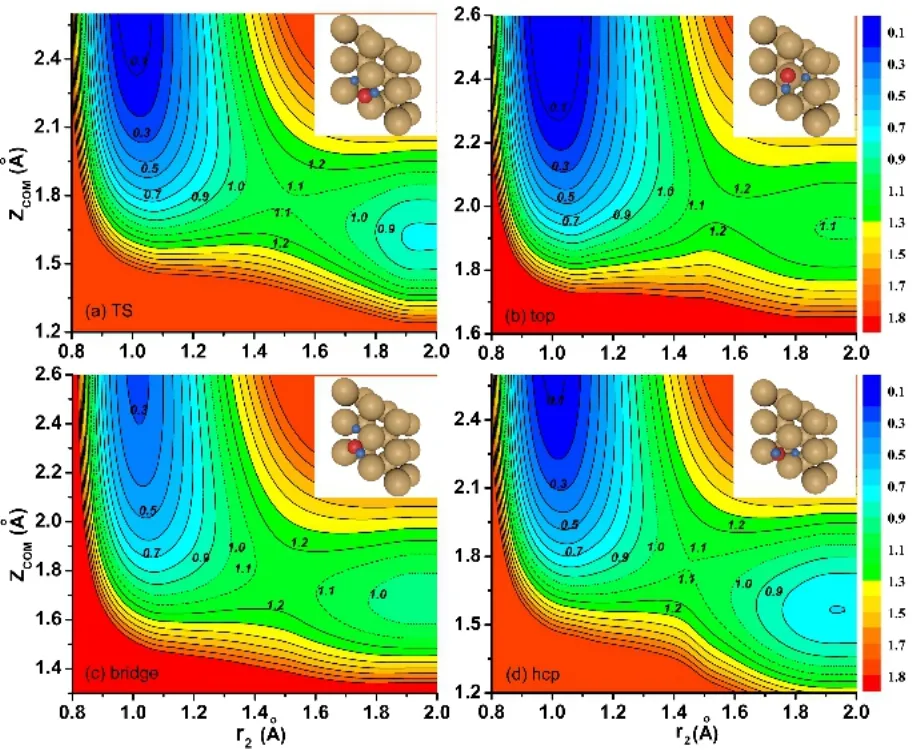
图10 在固定位置上，H2O在Cu(111)表面解离吸附的势能面等高线图83Fig.10 Fixed-site contour plots of the PES as a function of the vertical distance of H2O (Zcom) and the distance between the dissociating H atom and the center mass of OH (r2),with other coordinates fixed at the corresponding saddle-point geometries.The saddle point geometries are inserted in the right upper corner 83.

3 置换不变多项式神经网络(PIP-NN)

对于含有相同原子的化学反应，势能值应该对相同原子的置换保持不变。因此，置换对称性是势能面构建中需要考虑的重要因素。由于 NN函数关于相同原子的置换是不对称的，在两个或者两个以上相等核间距的情况下，势能值会出现不光滑的情况。这可能在准经典轨线计算中引入一些误差，但对量子反应动力学结果不会造成任何影响。我们在上述 NN的拟合过程中使用了对 H原子排序的方式来保证每个构型能量的唯一性。

为了严格处理这种相同原子的交换对称性问题，Jiang与Guo提出了PIP-NN方法38,39。他们从分子的键长出发，产生Bowman提出的一套置换不变多项式33,34，然后将这些多项式作为NN的输入层用于拟合。NN的输入层由低阶的置换不变多项式组成，也就是对称化的单项式，即其中pij= exp(-arij)，rij是核间距，lij是pij的阶数，是对称算符。是每个单项式的总阶数。值得提出的是，输入层中置换不变多项式的数量要足够多，以保证体系的置换对称性。基于PIP-NN方法，我们重新构造了HOCO体系和CH5体系的PIP-NN势能面85,86。这两个PIP-NN势能面更加适合于准经典轨线计算。尽管在构建PIP-NN势能面时又增加了一些从头算构型，但是量子动力学结果与之前NN势能面上的结果都吻合得非常好。

并且，我们还和复旦大学徐昕教授等合作，利用新一代泛函XYG387,88计算所有结构的能量，并用 PIP-NN方法拟合了一个新的 XYG3势能面89。我们发现XYG3能基本达到CCSD(T)的精度，计算得到的反应势垒和CCSD(T)结果很接近。基于 XYZG3势能面的量子动力学反应几率和速率常数与 CCSD(T)势能面的结果也很吻合。由于XYG3泛函远比 CCSD(T)计算速度快，可以将XYG3应用到更大的体系，尤其是H的一系列抽取反应。

4 基本不变量神经网络(FI-NN)

在PIP-NN方法中，神经网络使用置换不变多项式作为网络的输入层，理论上要求所使用的多项式包含所有的首要不变量和次要不变量。但随着体系的增大，输入层多项式的个数随次要不变量的最高次数呈非线性增长。以简单的A3B2体系为例，次要不变量的最高次数为 11，此时共有14984个多项式的次数小于等于 11。将这 14984个多项式全部作为神经网络的输入将导致网络参数过多，所以并不切合实际。所以在很多时候，PIPNN方法使用按一定次数截断的多项式作为神经网络的输入。对于A3B2体系，可以将次数限制在6次以下，这样便可以将输入层的多项式减少到525个。在A3B2体系中，由于截断次数小于次要不变量的最高次数，拟合时有一半左右的次要不变量将不能被考虑在内。

为此，我们提出了基本不变量神经网络(FINN)拟合方法40。这个方法能在保证对称性的前提下有效减少神经网络输入层多项式的个数，在保证势能面的对称性的同时能有效提高势能面的计算速度。

对于AiBj···Xp分子体系，我们使用原子核间距(r1,r2,···,rn)作为势能面的自变量，其中 n 是分子体系的键长个数。群 G = Si× Sj× ··· × Sp，是多个对称群的直积，其中Sn是n阶对称群。定义ˆg为置换操作，为群G的某个元素。

假设R是一个集合，包含所有关于r = (r1,r2,···,rn)的多项式。当R在加法和乘法运算下为阿贝尔群，且乘法对加法满足左右分配律时，R被称作多项式环。设RG是R的子环，其元素在ˆg的作用下保持不变，则RG是一个置换不变多项式环。RG是有限生成的并且有一个最小生成元集合，其最小生成元集合也可以称作基本不变量(FI)。有了基本不变量，我们就可以生成任意形式的置换不变多项式。下面我们将首先给出基本不变量的计算方法。

对于特定的分子体系，其基本不变量可以使用 Singular等软件计算90，计算时所用的算法是由King在2013 年提出的91。这里我们以A2B和A3B 体系为例，使用Singular计算其基本不变量，更多体系的基本不变量可在https://github.com/kjshao/FI中获得。

(1) 对于 A2B分子体系，基本不变量为(xi代表分子核间距)：

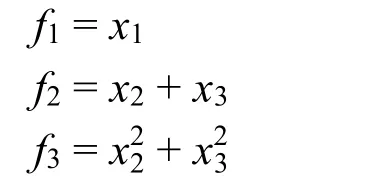
(2) 对于 A3B分子体系，基本不变量为(xi代表分子核间距)：

使用PIP-NN方法拟合势能面时，通过选择合适的截断次数，可以得到较好的拟合结果，并同时确保所使用的多项式数目不至于过多。但当分子体系增大时，只能选择较低阶的多项式，这会使是势能面的拟合结果达不到理想水平。同时，舍弃高阶多项式意味着拟合时所使用的生成元不完备，这也将导致额外误差的引入。相较于 PIP-NN 方法，FI-NN中输入层的多项式数目明显减少，将有效提高势能面的解析速度。

用PIP-NN方法构建的OH3体系的势能面，输入层总共使用了50个多项式，最高次数为4。但实际上，A3B体系的基本不变量只有上述的 9个，最高次数为3。新的OH3FI-NN势能面的拟合总共用了16814个ROHF-UCCSD(T)-F12a/augcc-pVTZ个从头算数据点，与之前用于拟合 OH3CXZ NN势能面所用的数据点相同。最终 FI-NN势能面的整体 RMSE、最大偏差为 1.18和 28.18 meV。并且，基于FI-NN和NN势能面的H + H2O以及其逆反应的反应几率都符合得很好，说明了FI-NN方法的可靠性以及拟合所得的势能面的精确性。

我们还比较了FI-NN和PIP-NN势能面的计算速度。对于较小的体系，多项式的计算基本不占时间，而神经网络的计算速度基本相同，所以整体而言，两种方法的速度相近。FI-NN方法的优势主要体现在对较大体系的计算上，对于更大的体系，FI-NN 的速度提升将会更为显著。

5 结论

精确的势能面是反应动力学理论研究的基础，只有可靠的势能面才能得出可靠的动力学计算结果。随着反应体系的增大和自由度的增加，精确的势能面构建给人们带来了很大的挑战92。本文主要介绍了近几年来，用神经网络方法构建多维体系的精确势能面的进展。这些势能面包括气相分子体系OH3,HOCO,CH5，以及H2O在Cu(111)表面的解离等。我们发展和完善了一套系统选择构型的方案，通过多次添加构型以及拟合，最终的基于神经网络构造的势能面拟合精度相当高，能够得到收敛的量子反应动力学结果。

我们基于置换不变多项式神经网络(PIP-NN)方法，重新构造了HOCO体系和CH5体系的势能面。这两个PIP-NN势能面更加适合于准经典轨线计算，但是量子动力学结果与之前NN势能面上的结果都吻合得非常好。

并且，我们通过使用基本不变量作为神经网络的输入，提出了一种新的置换不变势能面的拟合方法，称为基本不变量神经网络方法(FI-NN)。相较于其他方法，基本不变量的使用极大地减少了神经网络输入层多项式的个数，有效提高了势能面的计算速度。与其他方法相比，使用FI-NN方法可以得到很好的收敛结果，拟合误差可以达到相同水平或更小，同时还能有效加快势能面的计算速度。

总之，这些势能面构建方法的发展有望将反应动力学理论研究推广到更大更复杂的动力学体系。