基于矢量控制直流母线振荡抑制的研究

单宝钰, 曲诗健, 姜连生

(中国中车大连电力牵引研发中心有限公司，辽宁 大连 116022)

0 引 言

牵引控制系统由直流供电、预充电回路、滤波电路、牵引逆变器、异步电机组成。实际运行时，由于直流侧滤波电路和逆变器开关电路参数匹配，以及矢量控制算法在全速度范围内动态调节时，会使主电路出现负阻抗的情况。当出现负阻抗时，系统阻尼降低，此时直流侧电压和电流容易产生持续振荡，引起电机转矩脉动，设备发热，同时会使牵引控制系统进行过压、过流故障保护，严重时会损坏系统中的设备。

文献[1]介绍了更改LC参数的方法，这种方法在牵引系统设计初期可以采用，可实际运行时往往无法更改LC参数，由外部因素引起牵引系统的振荡。文献[2]中作者介绍了压频比控制振荡抑制控制策略，对定子电压进行补偿，为了改善电机负载输出电流振荡问题，属于对控制算法进行优化，有一定局限性。

针对系统参数、矢量控制算法等因素引起的直流侧电压和电流振荡问题进行深入研究，本文提出了一种通过动态调节转矩电流Isq给定值，即增加主电路正阻抗的方法，达到振荡抑制的目的。

本文通过建立数学模型，搭建Matlab仿真模型进行了仿真对比分析，提出了基于矢量控制振荡抑制控制策略，最后通过半实物仿真平台和地面联调试验，验证了本文提出方法的合理性和可行性。

1 基于振荡抑制控制策略研究

1.1 牵引系统主电路原理及振荡原因分析

1.1.1牵引系统主电路

牵引系统主电路原理图如图1所示。

图1 牵引系统主电路原理图

如图所示，牵引系统主电路由输入滤波电抗、预充电回路、支撑电容、功率模块、牵引电机组成，输入电压为DC750V。

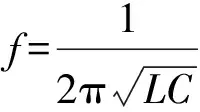
因此，直流母线电压、电流振荡主要是由控制不当、或者主电路LC参数不匹配引起的。

1.1.2振荡原因分析

目前直流供电接触网是由24脉波不控整流供电，当列车牵引功率增加时，直流网压下降，牵引逆变器呈负阻抗特性，系统阻尼降低，导致直流母线会在谐振频率点附近持续振荡[3]。当控制不当时，主电路无功分量增加，也会使主电路处于负阻抗状态，引起直流侧振荡。如果不进行抑制，会使得振荡不断发散，最终系统进行保护停止运行。

为方便振荡原因分析，本文简化了系统主电路架构，假设牵引逆变器的输出功率不变，忽略电路传动损耗，不考虑后端负载，则系统阻尼系数和稳定性条件为：

(1)

(2)

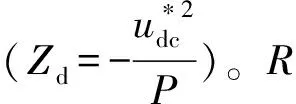
为了提高系统等效电阻，增加后端负载电阻阻值，即原系统等效阻值变为R′=R+RL。

因此，本文提出了一种牵引系统振荡抑制控制策略，在全速度范围内对振荡都会有效地进行抑制。

1.2 基于振荡抑制控制策略数学模型建立

考虑到直流母线振荡与LC参数匹配情况，调制策略、PI参数等因素有关，因此本文建立了异步电机数学等效模型、脉宽调制策略以及转子磁场定向矢量控制的定向线性化模型。并对牵引传动系统的整体稳定性进行了分析。先对基于矢量控制异步电机牵引系统稳态模型进行分析。

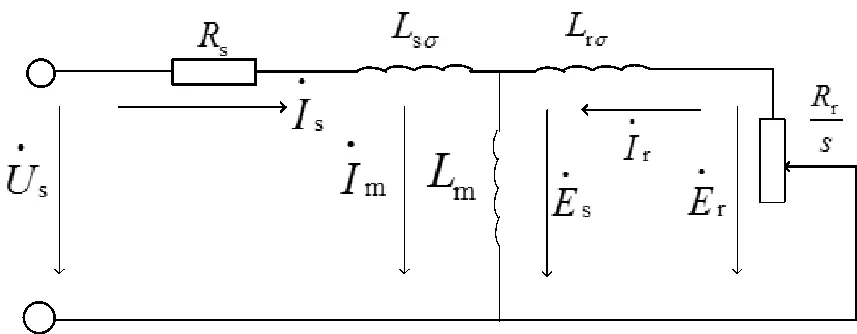
图2 异步电机稳态等效电路

如图2所示，在正弦稳态下，电压和电流空间矢量复变量形式如下：

(3)

稳态时电磁转矩为

(4)

由稳态模型可知，动态模型下电磁转矩等效数学模型为

(5)

式中，Te为电磁转矩；np为电机极对数；Lm为电路等效互感；Lr为等效转子电感；Isq为定子q轴电流分量；ψr为转子磁链[4-5]。

在牵引系统主电路中引入正阻抗可有效抑制振荡，由数学模型可知，通过改变电流转矩分量给定值，可以改变电磁转矩值，即调节主电路中正阻抗给定值。

异步电机输入三相电压是由逆变器开关管对直流母线电压Udc进行斩波合成后得到，其空间矢量可以表示如下：

us(t)=k(t)Ud(t)

(6)

其中，k(t)为脉宽调制(PWM)等效系数，Ud(t)为该时刻开关电压值。为了抑制直流侧振荡，可将上式k(t)定义为[6-8]

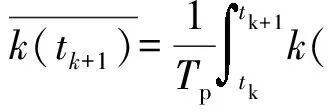
(7)

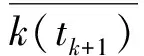
通过式(3)和式(4)可得空间电压矢量数学模型为

(8)

通过电压与电流关系可以推导出：

isq(t)≈Gc(p)isqref(t)+Gd(p)Ud(t)

(9)

式中，usref0和Ud0为稳态值，通过上式可知，通过对定子转矩电流分量isq进行动态补偿可以有效对振荡进行抑制。

通过对传感函数进行离散化后，将式(9)进行工程简化可得：

(10)

根据振荡抑制数学模型实时计算补偿电流值，对q轴电流实际给定值进行补偿，增加系统等效电阻。

1.3 基于振荡抑制控制策略仿真分析

为了对比分析单组逆变器和两组逆变器分别运行时，对主电路振荡情况进行仿真分析，通过Matlab建立了牵引系统仿真模型，模拟实际运行情况进行仿真分析[9-10]。仿真模型如图3、图4所示。

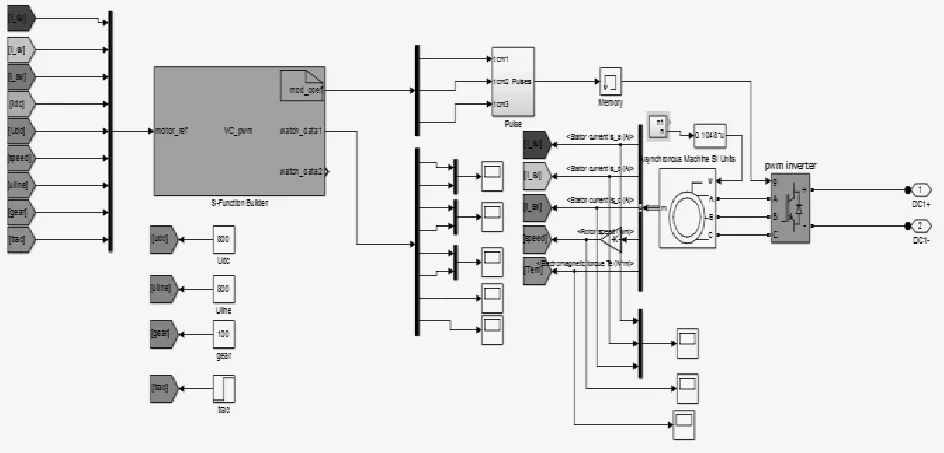
图3 牵引系统仿真模型

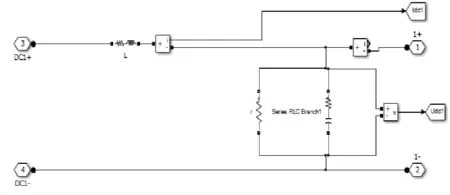
图4 主电路仿真模型

如图3、图4所示，仿真模型主要包括：基于S函数编写的转差型矢量控制程序，主电路模型、逆变器模型、电机模型、相应观测单元。

仿真试验说明：系统内部采样时间为400 μs，外围采样时间1 μs，网压Uline= 760 V，主电路电感值为L=1.5 mH，电容值C=6000 μF，线路等效电阻为Rline=0.15 Ω。电机参数与实际试验用参数相同，额定功率为120 kW，额定电压530 V，额定频率84 Hz，定子电阻0.01085 Ω，转子电阻0.008995 Ω，定子漏感0.000204 H，转子漏感0.000193 H，互感为0.004779 H，4极。

陪试电机转速n=1950 r/min，给定转矩100%，对比分析未加振荡抑制和加入振荡抑制两种控制策略波形情况。

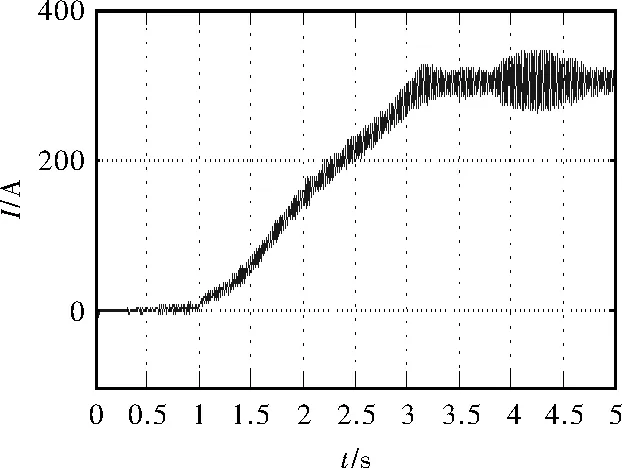
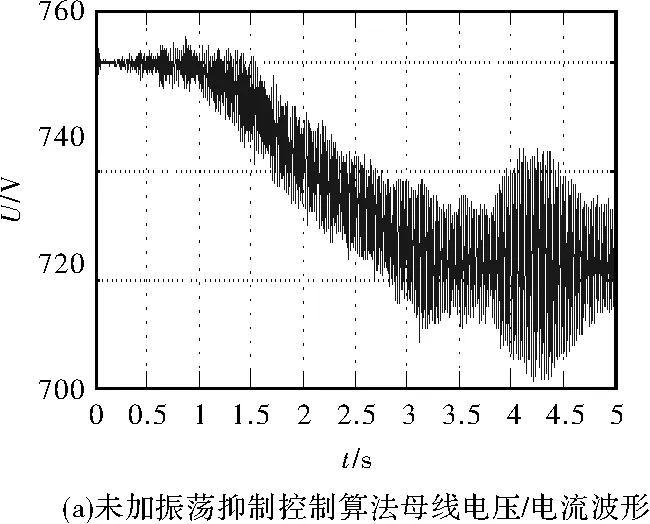
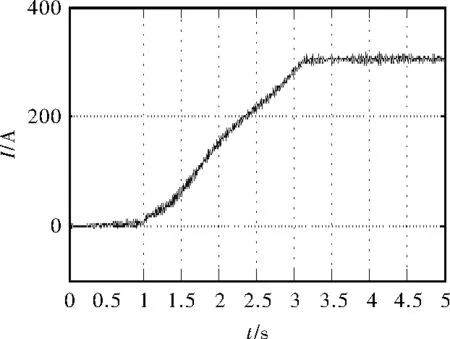
图5 电压/电流仿真波形

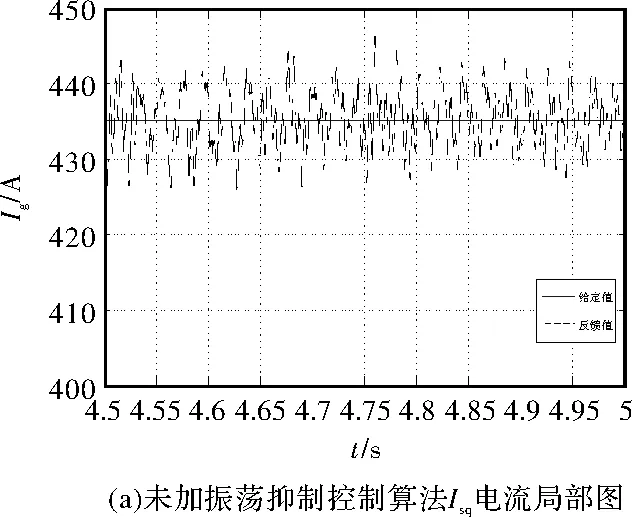
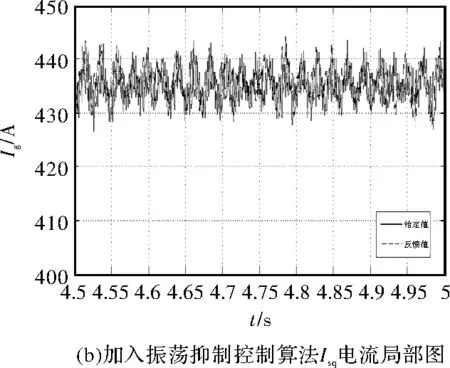
图6 Isq电流仿真波形

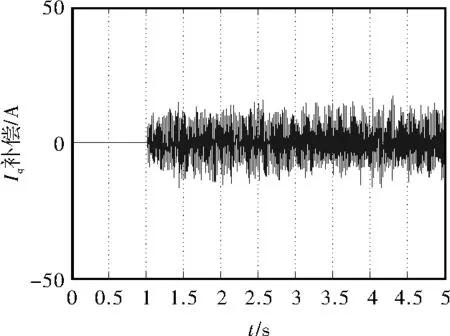
图7 Isq电流给定补偿波形

如上所示，未加入振荡抑制控制算法母线电压、电流、转矩在Isq电流给定值达到最大后产生振荡，电压振荡峰峰值为40 V，电流振荡峰峰值为80 A。

加入振荡抑制控制算法后，针对牵引系统的Isq电流给定值进行动态补偿，补偿后电压峰峰值为10 V，电流峰峰值20 A。

通过对比仿真结果可知，牵引系统运行在振荡速度段时，基于振荡抑制算法对转矩电流分量给定值进行超前调节，有效抑制了直流侧电压、电流振荡，验证了本文算法的合理性。

2 基于振荡抑制控制算法试验分析

试验设备：城轨100低地板铰接车用动力单元柜体、被试异步电机、陪试电机、陪试变频器、DL850示波器。控制单元如图8所示。

图8 牵引系统控制单元

试验条件：给定满转矩、直流供电电压750 V、速度给定1800 r/min，观测母线电压、母线电流、输出电流、输出电压波形，通过以太网与牵引控制单元进行通信，对比分析传统控制策略与本文提出控制策略结果，来验证本文提出方法的可行性。试验波形如图9所示。

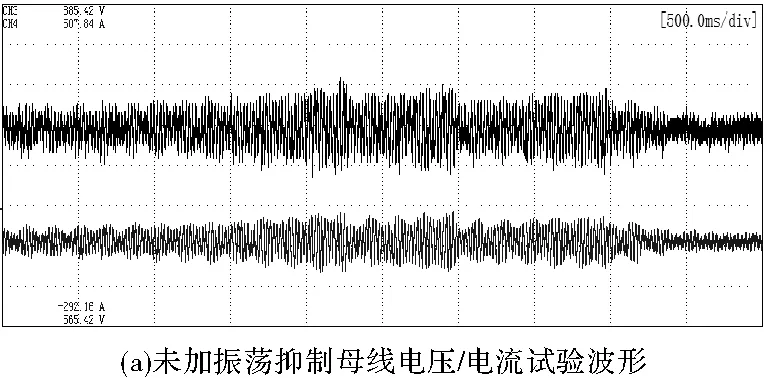
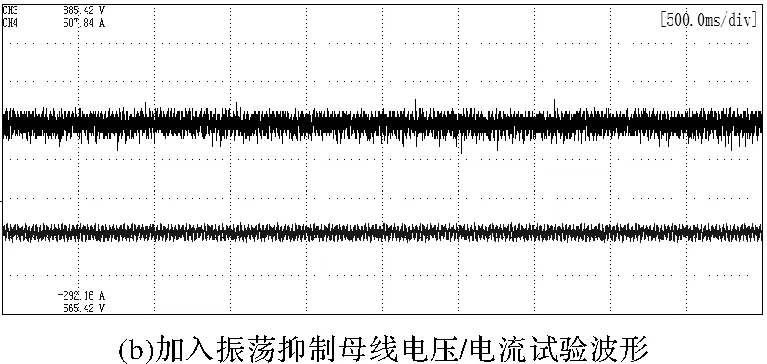
图9 电压/电流试验波形

如图9所示，CH3通道为母线电压波形(40 V/div)，CH4为母线电流波形(100 A/div)，未加振荡抑制控制算法的牵引系统直流侧母线电压/电流在速度为1800 r/min时产生振荡，振荡无法恢复，电压振荡峰峰值为65 V，电流振荡峰峰值为127 A，严重影响了系统的稳定性，当振荡得不到控制时，会导致停机保护，严重时会损坏设备。

当通过软件给定指令加入振荡抑制控制算法后，振荡得到有效抑制，电压波动峰峰值为8 V，电流波动峰峰值为4 A。

试验结果与仿真分析结果相符，验证了本文提出算法的合理性和可行性。

3 结 语

(1)本文提出了一种基于矢量控制异步电机振荡抑制算法，搭建了数学模型和仿真模型，通过仿真试验分析和地面联调试验结果分别验证了本文提出方法的合理性和可行性。

(2)通过试验结果表明，采用振荡抑制控制策略，试验结果与理论结果基本一致，达到预期，可以有效抑制直流侧电压、电流振荡，提高系统的稳定性。