微项目研探：呼唤儿童本位理念的回归

卜骥 周玲棣

【摘要】本文以“圆柱的表面积”自探教学为例，阐述了数学教学需要实现儿童本位理念的价值回归，“以学定教、以教导学”，让学生在具体问题情境中进行有效的自主探索活动，在“跌打滚爬”中“且探且思”，获得真实体验与真知。

【关键词】微项目 儿童本位 理念回归 数学案例

呼唤儿童本位理念的回归，是“以学定教、以教导学”小学数学课堂教学的方向标，也是本校江苏省十三五教育科学立项课题“观察·支持”儿童学习的教学策略研究的重要研究内容之一。“圆柱的表面积”是笔者执教的一节市级公开课，属于苏教版下册第二单元的知识。圆柱的表面积的教学应该基于“儿童本位”理念，寻求支持学生学习的教学方式、方法，重视让学生在具体问题情境中进行有效的自主操作、自主探索活动。让学生在“跌打滚爬”中“且探且思”，获得真实体验与真知。

一、课首微探，铺垫回探

针对即将进行的新课教学，教师设计了这样一组铺垫式的“开胃菜”，目的是让学生基于已学知识解决一些基础问题，为后面的学习打下基础，为成果自探“加油”，为下一层次学习“助力”。

微项目一：

1.口答下列各题：

（1）圆的半径是2厘米，圆的周长是多少？面积是多少？

（2）回忆长方体、正方体的表面积如何计算。你能算出它们的表面积吗？

2.我们前面已经掌握了长方体、正方体的表面积的计算方法，今天我们要来探讨圆柱表面积该如何计算。大家有信心学好吗？

这是为后续学习做好复习铺垫，有利于针对知识的“起点”和原点设计自探学习，同时也能激发学生学习积极性，在学生学习最近发展区提升学习力。

二、课中微探，围标自探

学生的知识获得不能全靠教师的“授鱼”，而应该设计一些环节“授渔”，给学生一片“水域”，让学生浸润在问题中，给他们“扑腾扑腾”的机会。学生经历“呛几口水”的过程，获得知识才更有“喜悦”和“味道”。教师结合教学目标给学生设计了这样的试探过程：

1.目标试探：圆柱的表面积的概念。

微项目二：

（1）你知道长方体、正方体的表面积指什么？如何求长方体、正方体的表面积？

（2）什么是圆柱的表面积？请用观察学具，小组观察、讨论、交流。

概括并得出结论：圆柱的表面积=圆柱的侧面积+两个底面积。

2.合作研探，出示例2：一种圆柱形的罐头，底面直径是11厘米，高是15厘米。它的侧面有一张商标纸，商标纸的面积大约是多少平方厘米？（接头处忽略不計）

微项目三：

（1）启思：你知道这道题是要我们求什么吗？（圆柱的侧面积）

（2）思考：求这个商标纸的面积大约是多少平方厘米，你打算怎么做？

（3）合探：商标纸展开图，即这个长方形的长和宽与圆柱有什么关系？怎样计算圆柱的侧面积？

（4）什么叫“接头处忽略不计”？

学生自探汇报：

（1）学生操作演示：学生运用自制的圆柱模型说明如何求剪开学具。

（2）呈现学生“学果”：侧面展开可能会出现以下几种情况：长方形、正方形、平行四边形。

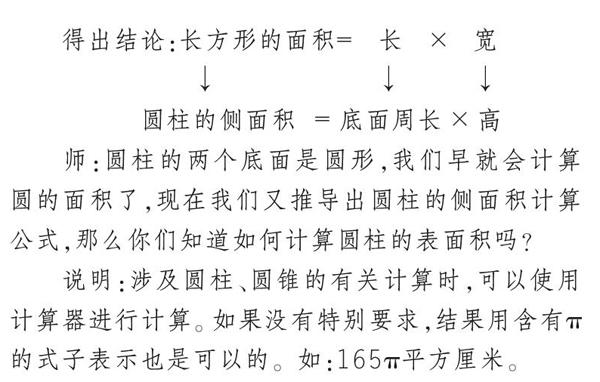
长方形的长等于圆柱底面的周长，宽等于圆柱的高。

得出结论：长方形的面积= 长 × 宽

↓      ↓   ↓

圆柱的侧面积  = 底面周长 × 高

师：圆柱的两个底面是圆形，我们早就会计算圆的面积了，现在我们又推导出圆柱的侧面积计算公式，那么你们知道如何计算圆柱的表面积吗？

说明：涉及圆柱、圆锥的有关计算时，可以使用计算器进行计算。如果没有特别要求，结果用含有π的式子表示也是可以的。如：165π平方厘米。

给学生设计一个自探过程，让学生先学先思，在经历思维完整过程中获得经验。教师的及时跟进能够帮助学生化解难点，消除困惑点，也能帮助学生充分感知形成的过程，为良好的知识建构打好基础。

三、课中再探，探标研究

探标研究，是朝向深度思维的一条路径。要想获得真知，就得培养学生“打破砂锅问到底”的精神，就得给学生设计一条可以登攀知识高峰的“藤索”，让学生思维有方向、有目标、有切入点，才能让学生思维品质的提升成为可能。

微项目四：

1.投影出示例3：把右边圆柱的侧面沿高展开，得到的长方形的长和宽各是多少厘米？圆柱的底面半径是多少厘米？

（1）这个圆柱的侧面沿高展开，得到的长方形的长和宽各是多少厘米？圆柱的底面半径是多少厘米？

（2）你能在下面的方格纸上画出这个圆柱的展开图吗？

（3）学生独立完成画图。

学探汇报，反馈订正。

2.固标练习：教材P12“练一练”第1、2题。

再次自探，让知识更加透明，学生自探操作后组织学生仔细观察研究。借助具象的图像，能让学生对圆柱的侧面展开后的形状有进一步的认知，对于巩固所学很有帮助。

四、课尾微探，固标练习

根据学习规律以及遗忘理论，对于新知的学习必须要经过一个“夯实”的过程。课尾固标练探，能够让学生更加明晰概念，知晓方法，夯实学习效果。

微项目五：

1.教材P13练习二第4、5、6、7题。

2.圆柱的表面积学习效果检测题。

（1）请填写：

圆柱的表面积=（            ）

圆柱的侧面积=（          ）

圆柱的底面积=（           ）

（2）把一个圆柱体的侧面展开，得到一个长31.4厘米，宽10厘米的长方形，这个圆柱体的侧面积是（   ）平方厘米，表面积是（    ）平方厘米。

（3）用一张边长是20厘米的正方形铁皮围成一个圆柱体，这个圆柱体的侧面积是（）。

以上练习设计，不仅巩固了所学，而且让学生知道了解决问题的方法是灵活的，还使学生亲自参与了对充满“挑战”的题目的探索，使知识掌握得更加牢固，并对旧知进行再创造并萌发了创新意识，也有利于挖掘优生的潜能，还能为求圆柱的体积埋下伏筆，将课堂的尾声又推向一个新的高潮。

五、教后反思

1.目标与学情结合。在设计微项目化教学的时候，教师不能一厢情愿地设计与实施教学预案，要求立足于学生的学习时态，灵活实施教学设计，不要过分去追求多花哨，多激情，多精彩，而要把精力放在课堂的本质上。教师必须以儿童本位为指导，时刻把握“教学目标”这根“缰绳”，关注“学情”，也要关注“深度”，否则数学课就缺乏了厚重和内涵。

2.自探与启思结合。在各个自探环节中，教师给学生设计一个属于学生的跌打滚爬的过程，让学生先学先思，在经历思维完整过程中获得经验。教师教学过程的每一次及时跟进能够帮助学生化解难点，消除困惑点，也能帮助学生充分感知形成的过程，为良好的知识建构打好基础。

每一个微项目问题情境的设计，都是为了激发学生学习“斗志”，为了把数学思维“激活”，为了让学生体验“成功”，获得最终探究的喜悦。所以，教师在知识建构与激发学生学习欲望之间，要善于“搭桥”，让学生始终保持那一份学习的“冲动”，这是优化微项目化教学的一大举措。

【注】本文为江苏省教育科学“十三五”规划课题“‘观察·支持儿童学习的教学策略研究”（课题/立项编号：D/2018/02/341）的阶段性研究成果。