RQ30D多传感器雷达在线测流系统数据可靠度分析
王少华 ,付京城 ,尼玛扎西 ,董 建
(1. 水利部南京水利水文自动化研究所,江苏 南京 210012;2. 西藏自治区水文水资源局阿里分局,西藏 阿里 859000)
0 引言
RQ30 天然河道测流系统是一种固定式雷达波流量监测系统,主要包括监测传感器和水力模型 2 个部分。RQ30 可同时采集流速和水位,流速传感器采用多普勒频移原理测量水体表面流速,水位传感器采用雷达脉冲传播时间原理测量当前水位。一经安装完成,RQ30 起点距一直固定不变。因此,要计算断面流量,需要通过内部模型处理观测到的特定位置的表面流速和水位,将二者转化成计算流量需要的平均流速和断面面积[1]。另一方面,RQ30 的内部模型并非借由人工测流数据率定得来,而是根据断面的形状和水位等信息通过专业水力模型计算得来,这也为脱离人工数据直接分析该仪器的可靠度提供了可能。
RQ30D(多传感器雷达在线测流系统)是RQ30 的衍生版本,其特点是利用至少 2 个测流传感器同时在一个断面测流,从而应对更宽更复杂的断面环境[2]。传感器增加之后,多个传感器拟合流量的可靠度是否能满足规范要求,是本研究分析的目的。
测量数据的质量主要由测量误差分析,测量误差按性质可分为以下 3 种误差:1)粗大误差。粗大误差是超出正常范围的随机大误差,是由测量过程中不可重复的突发事件(电子或机械噪声、操作人员的错误读数或记录、测量仪器的错误使用)所致,在数据处理前应该去除。2)系统误差。系统误差是数值不变或按某种规律变化的误差,是由理论、仪器、操作等不能完全满足测量标准所产生的误差。由于系统误差可以消除,因此,RQ30D是否与《河流测量测验规范》中提到的缆道测流数据存在系统误差不在本研究分析范围,本研究设定RQ30D 测量的流量数据与缆道测流数据之间的系统误差已经完成修正。3)随机误差。随机误差是一种在重复测量中按不可预见方式变化的测量误差,产生的原因无法控制,无法被消除,本研究的重点是分析随机误差。
根据《河流测量测验规范》要求,首先,流量测验的随机误差应服从正态分布[3]29,其次,随机误差的随机不确定度必须符合相关标准。随机误差的不确定度,是与测量结果有关,表征合理赋予被测量值的离散度的参数[4]。测量的不确定度表示由于测量中存在随机误差而使被测量值不能肯定的程度,它的大小反映了测量随机误差的变化范围,即反映了测量结果的可靠性,随机确定度越低,测量可靠度越高。
本研究采用 RQ30D 在高、中、低水时的实测数据,通过分析 RQ30D 误差的分布形态及测流数据的随机不确定度,分析测量结果的质量。
1 数据源获取
1.1 重复性条件的保证
研究测量数据的随机误差及其不确定度首先需要满足重复性条件,即相同测量程序、操作者、测量系统、操作条件和地点,并在短时间内对同一或相同类进行测量[5]。同时,由《河流测量测验规范》可知,当取置信水平为 95% 时,如果测量系列的样本容量 ≥ 30 个,则该次测量的随机不确定度为相对标准差的 2 倍[3]34。因此,原始数据的采纳一方面需要降低时间跨度以保证测量条件的重复性,另一方面还要确保数据样本容量 ≥ 30 个。
为满足重复性条件及样本容量的要求,本研究采用的数据取自西藏阿里地区狮泉河 RQ30D 在线测流站,选择该站数据作为样本的原因主要有以下 3 点:
1)狮泉河站上游有水库调节,高、中、低水对应的流量数据样本丰富,加之 RQ30D 测流数据为1 次/5 min,建成到现在积累的测流数据数量已经能满足分析要求。
2)由于 RQ30D 流量计算系统主要依赖断面形状和表面流速,而狮泉河断面岸坡经过水泥固化,河床由鹅卵石构成,河宽为 45~65 m,断面相对稳定,短时间内很难产生大的形状变化,可以满足测量条件。
3)因为狮泉河站流速相对较高,本研究采集的数据中,低水情况下最低流速 >1.3 m/s,可排除环境对表面流速的影响。另外,本研究选择样本时,也考虑了天气情况,根据气象信息尽可能选择少风的天气进行数据分析[6]。
1.2 数据样本的确定
根据狮泉河站历史资料显示,水位低于 5.0 m以下的是低水位,5.0~5.5 m 是中水位,5.5 m 以上为高水位,由此,本次选择分析的测流数据概述如表 1 所示。

表1 高、中、低水测流数据概述表
表 1 中各水位级样本容量均 > 40 个,可以将每组数据的样本流量均值作为 RQ30D 测流的约定真值参与分析,从而采用如下公式推算误差:

将表 1 中的数据带入公式(1),计算出各组数据的约定真值,然后通过公式(2)计算出各组数据的误差,误差值如表 2 所示。
2 误差分布形态分析
2.1 低水误差分析
Excel 自带的 frequency ( )和 normdist ( ) 函数,可以返回一组数据的频率和正态分布值。要利用frequency ( )和 normdist ( )函数,需要先对数据进行分组。分组,就是确定数据横轴坐标的起止范围和每组数据的起止位置,选取 1 个比最小值小的恰当的值作为第 1 组数据的起始坐标,然后加上合适的分组组距,直到最后 1 个坐标比所有数据的最大值大为止。分组中涉及极差、分组数计算及组距估算。
1)极差计算。公式如下:
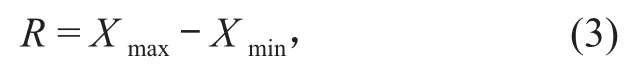
式中:R 为该分组数据的极差;Xmax为该分组数据的最大值;Xmin为该组数据的最小值。
2)分组数计算。公式如下:

式中:L 为该分组的数量;n 为该分组数据的总数量。3)组距估算。公式如下:

式中:ι 为组距,一般略大于极差除以分组数量。
由公式(3)~(5),计算得出低水测流误差的极差为 1.82 m3/s,分组数为 6 个,组距估算为 0.304 m3/s。将结果带入 frequency( )和 normdist ( ) 函数,得到低水测流误差的样本数量和正态分布值,然后将其转换成图表,结果如图 1 所示。
由图 1 可以直观看出,低水测流数据的随机误差服从正态分布。

表2 高中低水流量数据绝对误差值表m3/s

图1 低水流量随机误差分布图
2.2 中水误差分析
同样由公式(3)~(5),计算得出中水测流误差的极差为 4.51 m3/s,分组数为 6 个,组距估算为0.752 m3/s。将结果带入 frequency ( ) 和 normdist ( )函数,得到中水测流误差的样本数量和正态分布值,然后将其转换成图表,结果如图 2 所示。

图2 中水流量随机误差分布图
由图 2 可以直观看出,中水测流数据的随机误差也服从正态分布。
2.3 高水误差分析
由公式(3)~(5),计算得出高水测流误差的极差为 11.17 m3/s,分组数为 6 个,组距估算为 1.862 m3/s。将结果带入 frequency ( ) 和 normdist ( ) 函数,得到中水测流误差的样本数量和正态分布值,然后将其转换成图表,结果如图 3 所示。

图3 高水流量随机误差分布图
由图 3 可以直观看出,高水测流数据的随机误差同样服从正态分布。
3 数据的不确定度分析
《河流测量测验规范》对流速仪法单次测流允许误差有相应描述,其中对测量不确定度的规定是在置信水平为 95% 的前提下,允许误差如表 3 所示。由于流速仪法是目前测流的唯一标准,因此本研究采用该组数据衡量 RQ30D 测流数据的可靠性。
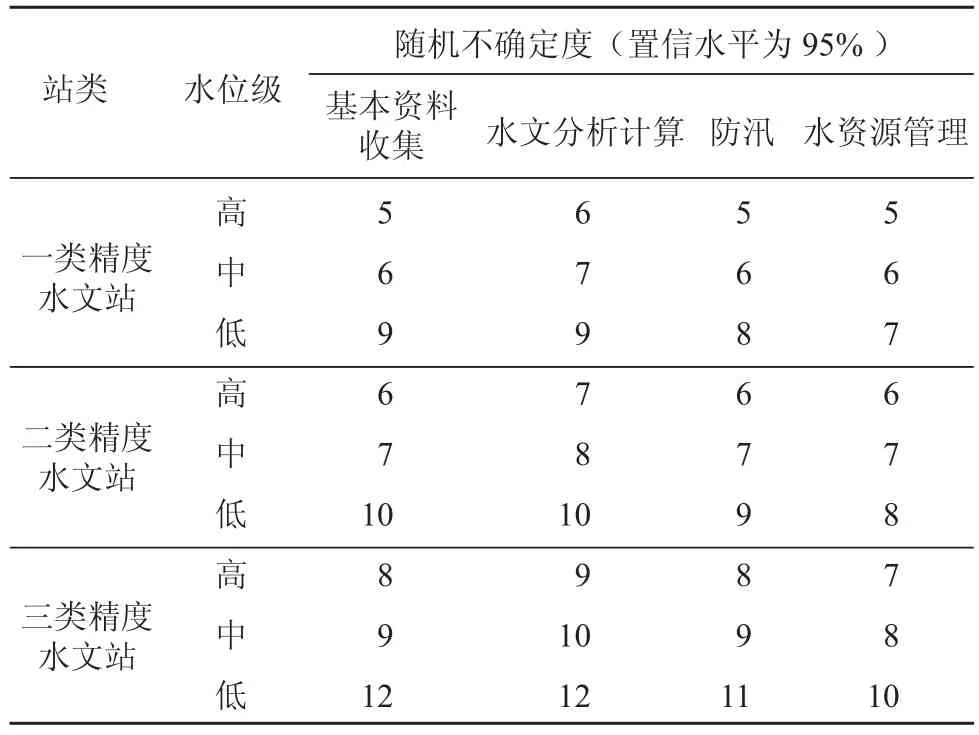
表3 流速仪法单次流量测验允许误差%
《河流测量测验规范》指出,当测流系列的样本容量 ≥ 30 个时,取置信水平 95%,则相对不确定度为相对标准差的 2 倍,相对标准差 S 由以下公式推算:

将表 2 中的数据带入公式(6),可得出 RQ30D取置信水平为 95% 的前提下,高、中、低水测流数据的不确定度分别为 3.90%,3.59% 和 3.87%。
由表 3 和计算出的不确定度可知,RQ30D 数据不确定度满足规范要求,测流数据可靠度较高。
4 结语
RQ30 目前在国内应用较多,其针对固定式雷达的测流模型较为先进,经验表明,当 RQ30 系统采用单个传感器时,可以输出稳定可靠的流量数据。本研究基于《河流测量测验规范》,研究了RQ30D 这种多传感器工作模式下的测验数据,通过随机误差分布形态及随机不确定度 2 个角度分析,可发现 RQ30D 系统的高、中、低水数据均符合《河流测量测验规范》要求,测流数据可靠度较高,是一种可以实现大江大河在线测流现代化的测流方法。

