斜吊杆下承式系杆拱人行天桥振动设计

马中文，刘 峰，汪 剑

（武汉市政工程设计研究院有限责任公司，湖北 武汉 430015）

0 引言

近年来，在城市建设突飞猛进的形势下，城市人行天桥的建设也得到了高速发展。随着新材料、新结构体系、新施工方法及新结构分析方法的广泛采用，同时考虑到桥墩布置困难及管线等诸多因素影响，人行天桥正朝着轻质、大跨、纤柔的方向发展。但对于这种大跨轻柔人行天桥，其结构刚度小，自振频率低，阻尼小，在行人、地面汽车等外界荷载的激励下，容易引发大幅度振动，会给行人带来不适感，行人在行走过程中会出现紧张甚至恐慌的心理，由此直接导致人行桥结构适用性能的降低。

目前国内现行规范仅仅通过控制结构自振频率来控制舒适度，该规定过于简单，这远远不能满足实际评价的需要，而国外相关规范一般通过自振频率和加速度双控来保证结构动力特性满足使用要求。因此本文以某斜吊杆下承式系杆拱人行天桥为背景，对其在人行荷载激励下的振动响应进行分析，参照相关规范对其舒适度进行评价，并在此基础上提出相应的振动控制措施，为类似人行天桥设计提供参考。

1 某斜吊杆下承式系杆拱人行天桥结构设计概况

某人行天桥主要连接综合体育馆及其另一侧的有轨电车站，重点解决车站客流进出综合体育馆的问题，便于未来举办体育赛事时快速疏散人流。经综合比选采用梁-拱组合结构，跨径布置为2.2 m+14 m+43 m+5.55 m=64.75 m。其中，主梁主跨长43 m，全宽5.8 m，外侧挑梁钢管最宽处全宽为9.8 m。主跨采用斜吊杆下承系杆拱结构形式，按刚性系杆柔性拱设计。主跨由主拱肋、系杆钢箱梁、吊杆三大部分组成。

1.1 拱肋及挑梁

中间主拱肋采用竖直拱面，拱轴线为二次抛物线，矢高为11 m，跨径43 m，矢跨比为1/3.91。主拱肋采用Φ600 mm无缝钢管，挑梁钢管采用Φ402 mm无缝钢管制造，平面线形为R=183.206 6 m的圆曲线。

1.2 系杆钢箱梁

系杆钢箱梁为鱼腹型钢梁，梁高1.2 m，箱宽为5.8 m。桥面为正交异性钢桥面板，顶板、底板及腹板一般厚度为16 mm，局部厚度增大。横隔板采用实腹式横隔板，标准间距2.0 m。

1.3 吊杆

拱桥吊杆按空间倾斜的双索面布置，上端锚固于拱肋钢管，下端锚固于挑梁钢管。吊杆在拱肋上的纵向布置间距为1.5 m，在主梁上的纵向布置间距为2 m。本桥吊杆采用型号为OVM RM5-13的平行钢丝吊杆。吊杆分为左、右两排，每排17根。

天桥三维模型及主梁断面见图1，经计算分析，本天桥结构强度及刚度均满足相关规范要求。

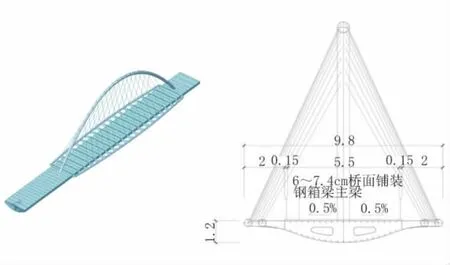
图1 主梁空间模型及主梁断面（单位：m）

2 人行天桥振动设计

行人步频具有明显的窄带随机性，基本分布在1.6～2.4 Hz之间，当桥上行人较多时必然有一部分人步频接近而产生同步效应，当这一同步频率与桥梁的某阶自振频率接近时，就会产生人桥共振现象，会给行人带来不适感。一般而言，正常设计施工和使用的人行天桥可能存在振动过大导致舒适性较差的问题。

从原理上看，人行荷载引起的人桥系统的振动是影响舒适性的直接原因，涉及的问题包括两方面，一方面是人行荷载下人桥系统的振动问题，另一方面是人桥系统振动中行人的舒适度问题。目前各国的人行桥设计规范中对正常使用状态下的行人舒适度都有相应的规定，通常是以控制自振频率（或周期）和控制加速度来保证结构动力特性满足使用要求。

人行桥的振动设计主要步骤如下：

（1）全桥结构动力特性分析，确定各阶频率和振型；

（2）选用合适的行人密度计算最大加速度响应，按照相关规范或指南评定舒适度指标；

（3）若使用性能不达标，确定要采取的减振措施。

2.1 人行天桥动力特性分析

动力特性分析是指求解结构的固有频率和振型，固有频率是结构自身的振动特性与荷载无关，主要是由结构形式、质量分布、材料性质、连接情况等决定的。本文采用MIDAS Civil软件计算出了结构的前20阶自振频率和振型，结果见表1，相应的振型见图2，振型主要包括水平振动、竖直振动和侧向扭转等。

表1 天桥前10阶自振特性

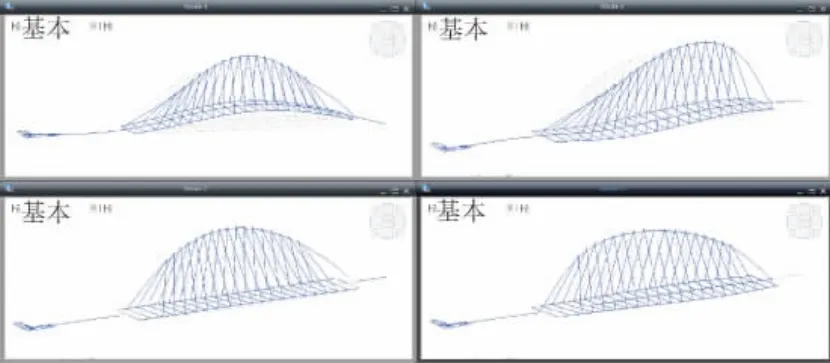
图2 天桥前四阶振型图

按照国外相关规范建议，设计应尽量避免人行桥的竖向振动固有频率落在1.6～2.4 Hz和3.5～4.5 Hz的范围内，由表1可见，本天桥第一阶振型为一阶竖向振动，其自振频率为2.80 Hz，二阶竖向振动，其自振频率为4.74 Hz，符合相关规范建议，但不符合我国《城市人行天桥与人行地道技术规范》（CJJ 69—95）2.5.4条规定的“竖向自振频率不应小于3 Hz”的要求。因此有必要通过控制人行荷载作用下结构最大加速度响应来保证结构动力特性以满足天桥使用要求。

2.2 人行天桥最大加速度响应分析

行走对人行天桥的作用可用简谐荷载共振模型描述，国内外对于单个行人的不同行走状态均进行了广泛而深入的研究。竖向行人荷载可按BS5400取值，单人验算动荷载为：

式中：vt为单人荷载在桥上的移动速度；f0为桥梁竖向基频。

对于大量相互独立的行人来说，行人前后间距较小，行人已不能自由的按照本人意愿和习惯行走，因此持续的高密度人群在桥上的流动可以比拟为连续的物质流，相互同步的概率要比低密度人群大很多，只是相位不同，按照随机概率分布模拟方法，总结出高密度条件下等效行人数计算公式为：

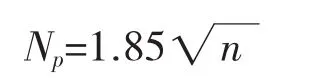
式中：n为人行天桥上行人总数量。

本文利用软件MIDAS Civil软件将行人脚步动荷载函数加载于该桥上，得到该桥跨中的加速度时程曲线，见图3。

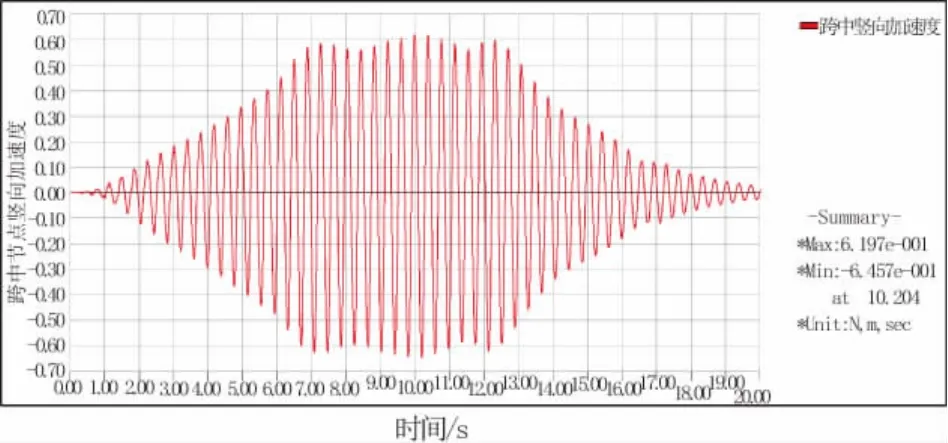
图3 天桥在人行荷载作用下跨中节点加速度时程曲线

从图3中可以看出，本天桥在高密度人群工况下，加速度响应峰值为0.62，按照相关规范建议（见表2），可评定为中度舒适，考虑到本天桥的特殊性，为了提高安全性能和使用性能，有必要对本天桥振动进行控制。

表2 人行天桥舒适度等级

2.3 人行天桥振动控制

针对钢结构人行天桥的振动控制措施主要有传统的增大结构的刚度和较新颖的增大结构的阻尼两种。当人行天桥的截面和跨度受到比较某些特定因素的限制时，单纯通过优化人行天桥结构本身有时仍不能避免其过量振动，此时行之有效的做法是在人行天桥中设置调频质量阻尼器（TMD）系统，进行消能减振处理。

调谐质量阻尼器是由弹簧、阻尼器和质量块三者组成的减振装置，其目的是将振动能量向调谐质量阻尼器中传递，并通过TMD系统中的阻尼器耗散。

根据相关文献，为控制正弦荷载激励作用下的加速度响应，TMD优化参数可通过以下过程确定：

（1）选定TMD质量与减振模态广义质量的比值，一般取值0.01～0.05；

（2）确定最优频率比和最优阻尼比，并计算调谐装置的频率fd=αopt×fs，其中最优频率比和最优阻尼比的公式如下：

（3）计算TMD的物理参数阻尼器的质量、阻尼器的刚度以及阻尼器的阻尼公式如下（Mj为第j阶受控振型的模态（广义）质量）：

根据上述TMD设计参数及人行荷载模式，建立带TMD系统的MIDAS Civil计算模型，6个TMD布置在天桥箱梁中部，见图4。

图4 天桥主梁TMD布置示意图（单位：mm）

对于本天桥设置TMD后，跨中节点加速度时程曲线见图5。从图5中可以看出，加速度响应峰值为0.46 m/s2，竖向加速度减小达26%，效果较为明显，按照相关规范，天桥可评定为很舒适。

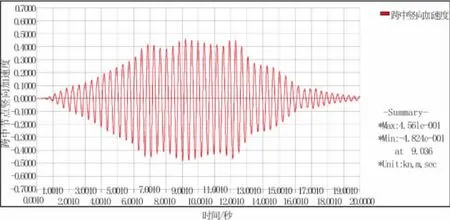
图5 天桥设置TMD系统后在人行荷载作用下跨中节点加速度时程曲线

3 结 语

人行天桥正朝着轻质、大跨、纤柔的方向发展，但其结构刚度小，自振频率低，一般竖向自振频率在1.8～2.8 Hz之间，目前国内现行规范仅对自振频率进行控制，方法过于简单，且没有明确的动力设计及行人舒适度评价方法，因此本文以某斜吊杆下承式系杆拱人行天桥为背景，参考国外相关规范对天桥振动设计进行研究，其结果表明，在不增加结构截面尺寸的前提下，可以从优化结构动力特性出发，进行详细的动力分析和减振设计，以达到人行桥的使用舒适性指标要求。