欠约束多机协调吊运系统动力学工作空间分析
苏 程, 叶佳楠, 李 巍, 丁旺才, 赵志刚
(兰州交通大学 机电工程学院, 兰州 730070)
用小型吊运设备组合形成一个大负载紧耦合多机联合吊运系统,从实用性、经济性等方面考虑都是值得期待的.为了使系统结构简单,一般情况下该类紧耦合系统为典型的欠约束定位系统.可应用于战时桥梁的快速架设,以及民用桥梁的分段精确定位架接等.从类型上讲,多机协调并联吊运系统属于柔索并联机器人系统,但与传统意义柔索并联机器人又有很大的区别,后者将柔索的一端固定做成特定的运动机构,通过调整柔索长度以实现被吊运物的期望运动位姿,其本质是一个单体机器人,故系统结构可重组性、通用性和模块化显得不足.多机协调并联吊运系统是由模块化串联吊运机构组成,模块化串联吊运机构可以是飞行机器人、工业机器人和常规起重设备等.欠约束多机协调吊运系统通过调整串联吊运机器人机构末端位置和柔索长度实现被吊运物的位姿,故欠约束多机协调吊运系统具有很大的灵活性、通用性和工作空间.
目前国内外关于欠约束多机协调吊运系统的研究刚刚起步,柔索并联机器人的研究成果可为该类多机器人系统的研究提供有价值的借鉴.欠约束多机协调吊运系统的一个主要研究方向是利用多架无人直升机来实现三维空间吊运操作.有许多学者探讨了多直升机吊运系统的运动学、动力学模型,并分析了系统的空间配置及稳定性[1-5].
另一个研究方向为多地面机器人系统对物体的吊运操作.Zi等[6]建立了3台起重机吊运一个重物的运动学和动力学模型,并分析了其工作空间,但只考虑了起重机末端的投影点始终保持正三角形的情况,且仅能变化绳长来改变重物姿态,起重机的末端是固定不动的,这种情况下多机系统与单体绳牵引并联机器人类似.也有学者应用运动旋量斜率对多机器人吊运系统的运动稳定性进行了研究[7].近年来赵志刚等[8-12]建立了多机协调并联吊运系统的正逆运动学、动力学模型,并探讨各种构型下系统的求解方法,同时分析求解了系统的静态工作空间.
对于欠约束多机协调吊运系统来说,动力学工作空间可以拓宽系统的运动范围,到达一些特定的位姿,故研究系统的动力学工作空间是非常有必要的.动力学工作空间是指被吊运物满足动力学方程时,被吊运物质心所在的空间位姿的集合.文献[13]中利用Farkas和Stiemke引理对不完全约束和完全约束两类绳牵引并联机器人工作空间的边界进行了研究,其在仿真过程中,固定了参数值,这样只给出了二维的层图.本文将在其基础上,利用Farkas和Stiemke引理,求解前人研究较少的欠约束多机协调吊运系统的动力学工作空间,同时利用蒙特·卡罗方法,数值求解得到系统动力学工作空间的整体效果图.
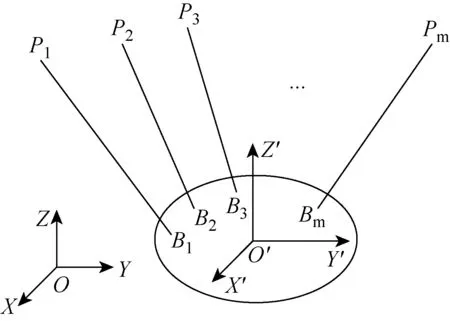
图1 系统示意图Fig.1 Schematic diagram of system
1 系统动力学建模
图1所示为m台吊机通过绳索牵引n自由度被吊运物的示意图.图中,每个吊机末端通过一根绳索与被吊运物连接.绳索与吊机末端的连接点为Pm,可通过改变连接点Pm的位置和改变绳长来实现被吊运物的位姿变化.绳索与被吊运物的连接点为Bm.
建立全局坐标系O-XYZ,在被吊运物质心上建立局部坐标O′-X′Y′Z′.被吊运物质心O′在全局坐标系O-XYZ的位置为
r=[xyz]T
(1)
设被吊运物的质量为M,重力加速度为g,则重力用零节距的单位旋量在全局坐标系表示为
G=-Mg[ir×i]T,i=[0 0 1]T
(2)
被吊运物在全局坐标系的速度和角速度分别为
被吊运物在局部坐标系中的惯性矩阵为I,则在全局坐标系中的惯性矩阵为
I′=RIRT
(5)
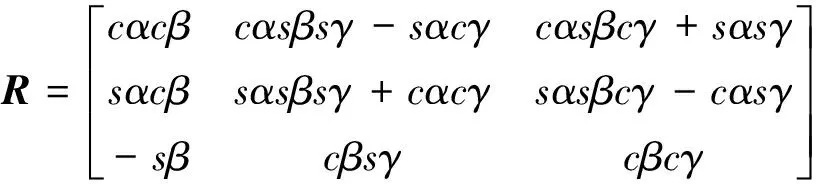
(6)
式中:R为局部坐标系相对于全局坐标系的旋转变换矩阵;γ、β和α分别为局部坐标系相对于全局坐标系的X、Y和Z轴的旋转角度;c和s分别为cos和sin.设每根绳的张力分别为T1,T2, …,Tm,对被吊运物利用牛顿-欧拉方程可得
(7)
式中:I3为3×3单位矩阵;T=[T1T2…Tm]为m根绳的拉力组成的m维列矩阵.
对式(7)进行变形,则被吊运物的动力学方程可表示为
AT=C
(8)
式中:C为n维列矩阵,表示作用在被吊运物上的所有外力旋量之和(包括被吊运物的重力、惯性力等),
(9)
满足
A=[e1e2…em]∈Rn×m
(10)
矩阵A是由m个旋量ei构成,
(11)
li=Pi-RBi-r
(12)
i=1,2,…,m
式中:Pi为机器人位置Pi在全局坐标系下的位置矢量;Bi为绳与被吊运物的连接点Bi在全局坐标系下的位置矢量.
2 动力学工作空间条件分析
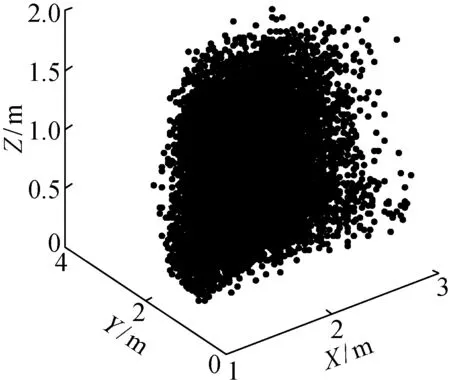
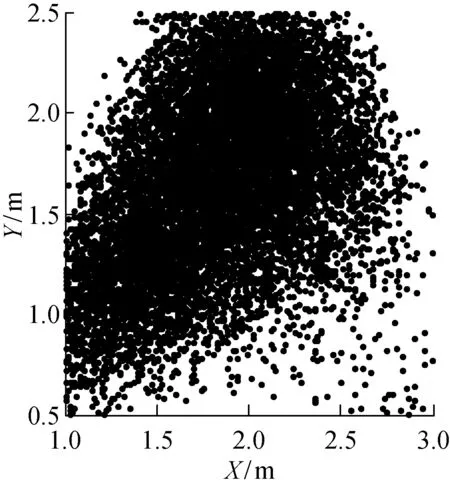
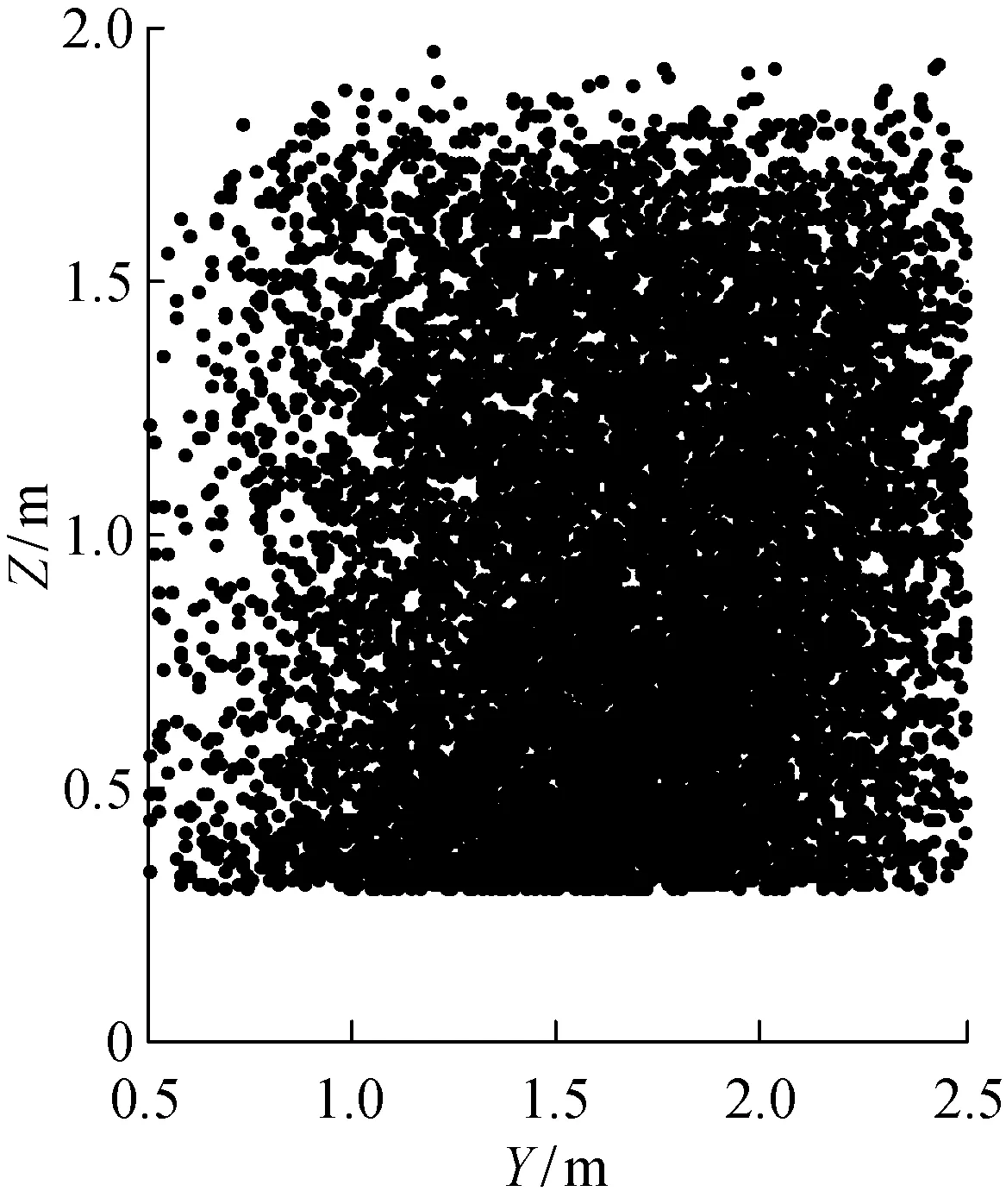
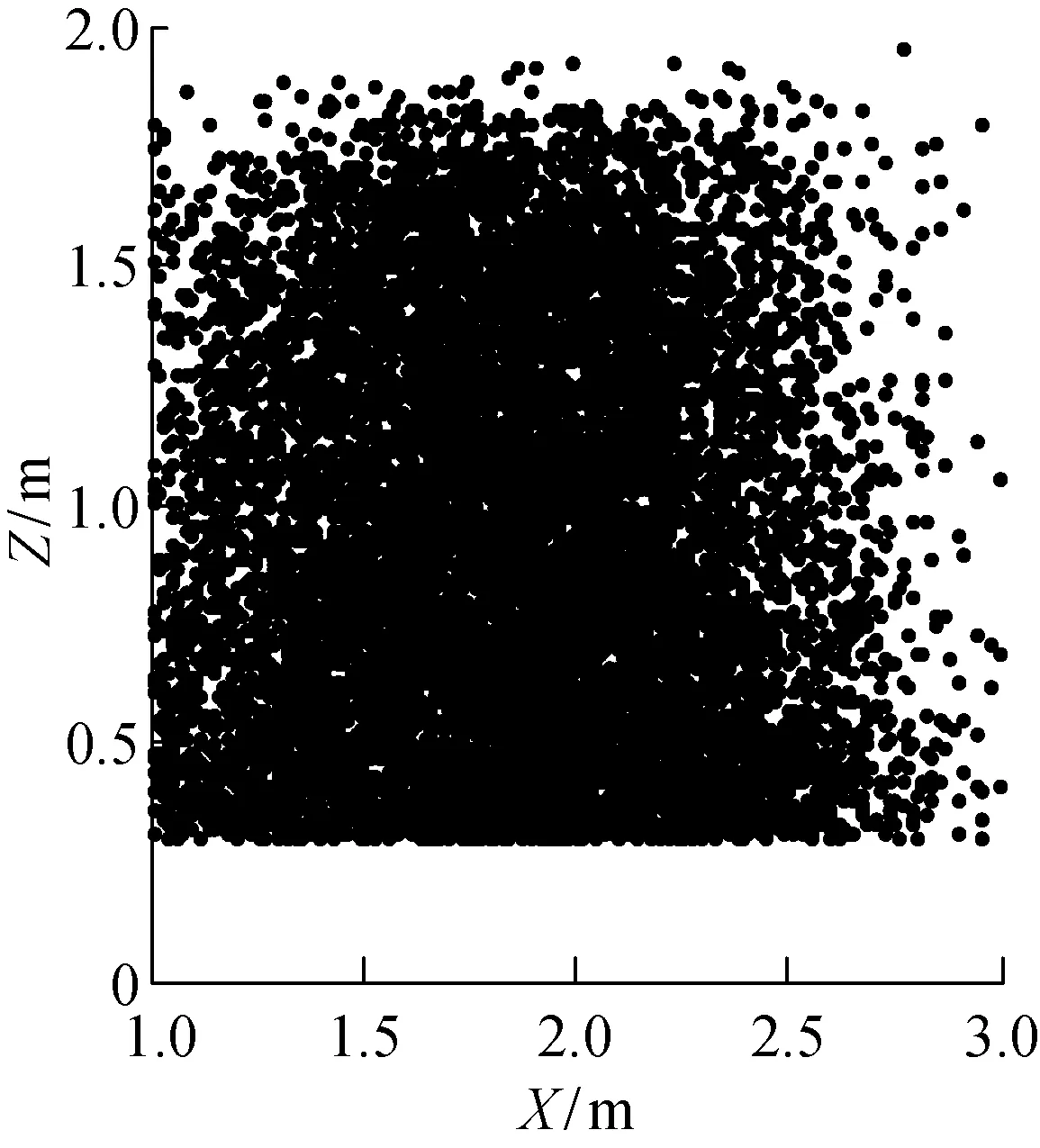
首先对m≥1+n时的过约束、完全约束系统和m=n时的不完全约束系统的动力学工作空间做简要分析.随后主要讨论m (1) 当m≥1+n时,可利用矢量封闭原理的求解方法,结合蒙特·卡罗算法随机产生单个机器人工作范围内的位置坐标或者利用扫描法逐行产生单个机器人的位置坐标.当m≥1+n时满足矢量封闭原理的条件,在结构矩阵A不发生降秩的条件下,AT=C可以转换成如下形式: T=A+C+(Im-A+A)k (13) 式中:A+为结构矩阵A的M-P伪逆;k为m维的任一向量;Im为m×m的单位矩阵.要保证每根绳的拉力Ti都大于零,根据矩阵的相关知识,只要式(13)中的右边第2项足够大时,就能使T中的每个元素都为正.因此,(I-A+A)中每个元素都为正时,能保证T中的每个元素都为正. (2) 当m=n时,可以将重力看成一根特殊的虚拟绳索,该绳的方向始终为重力方向,拉力大小为重力大小,这样相当于有m+1根绳,使其满足力封闭条件,这时动力学方程可变换成: (14) 式中:j=[0 0 -1 -yx0]T.这样也可以利用力封闭求解算法,并结合蒙特·卡罗算法随机产生单个机器人工作范围内的位置坐标或者利用扫描法逐行产生单个机器人的位置坐标. (3) 当m 由于动力学方程AT=C的形式满足动力学空间的标准是每根绳的拉力都大于零(即T>0),在研究过程中可以考虑T=0的时候作为工作空间的边界,所以动力学工作空间的条件可以表述为 AT=C,T≥0 (15) 本文基于Farkas和Stiemke引理分析欠约束多机器人绳牵引系统的动力学工作空间条件: (1) 基于Farkas引理分析.设A∈Rn×m,C∈Rn,则下面2组关系式: 有且仅有一组有解. Farkas引理的几何解释是考虑q作为一个分离超平面的法向量,这个超平面分离了2个集合,一个是由A中各个列向量组合而成的凸锥,另外一个是向量C.这个凸锥是A中所有单位旋量ei组成的空间.如果向量C不属于这个凸锥的空间,则说明这个超平面存在,这样式(17)有解,也就说明式(16)无解.因此,要使动力学工作空间的条件成立,即式(16)有解,就必须不能形成分离的超平面. 这其中有一种特殊情况,C位于超平面上,这样CTq=0,显然式(17)无解,这样式(16)也有解.由于q是法向量,是一些向量的叉积而成,不可能为零向量,对于CTq=0,会有2种情况:①C≠0,这样会导致部分的绳拉力大小为零,可以作为工作空间的边界.②C=0,零向量必共面,如果C=0,则式(15)变成了如下形式: AT=0,T≥0 (18) 从式(18)可以看出,总存在一组解T=0使式(18)成立.如果T=0即每根绳的张力都为0,但从实际的角度,不可能每根绳的张力都为0却能对被吊运物实施牵引运动.因此,式(18)将变成如下形式: AT=0,T>0 (19) 对于式(19)可以利用Stiemke引理进行分析. (2) 基于Stiemke引理分析.设A∈Rn×m,则下面2组关系式: 有且仅有一组有解. Stiemke引理的几何解释是考虑q作为一个支撑超平面的法向量,使凸锥A位于这个支撑超平面的一边.如果这个支撑超平面存在,这样式(21)有解,也就说明式(20)无解.因此,要使动力学工作空间的条件成立,即式(20)有解,就必须不能形成支撑超平面. 总之,通过对Farkas和Stiemke引理的几何解释可以看出,要使达到动力学工作空间的条件即式(16)或式(20)有解,就不能形成分离超平面或支撑超平面. 动力学工作空间的求解方法是先通过动力学方程组判断属于哪类超平面,再利用单位旋量ei通过不同的组合形成待测定的超平面,然后再测试剩余的单位旋量ei和C来判断待测定的超平面是否是分离超平面或支撑超平面,在测试的过程中需要测试所有可能的组合形式,来排除形成分离超平面或支撑超平面的可能性.具体测试步骤如下: (1)A是由m个单位旋量ei构成,每个单位旋量是一个n维的列向量.由于超平面是n-1维子空间的平移,因此,待测定的超平面由n-1个线性无关的单位旋量构成,超平面的法向量是n-1个单位旋量的叉积,可以表示为 (22) 式中:kn为标准的基向量;ei,j为第i个单位旋量的第j个元素. (2) 根据2个引理测试待测定的超平面是不是分离超平面或支撑超平面: 在测试的过程中存在sgn=0的特殊情况,对于Farkas引理,如上述提及的当C位于超平面上的情况,这样sgn(CTq)=0.由于法向量q是n-1个单位旋量的叉积构成,同时A中的单位旋量是线性无关的,所以q不可能为零向量.那么存在sgn=0的特殊情况的原因除了上述提到的C=0时的情况,另一种解释是C≠0,但位于超平面上,剩余没有形成q的单位旋量必位于超平面的一边.由于AT=C,是由单位旋量通过非负的组合形成C,同时单位旋量不可能为零向量,但是位于超平面一边的剩余单位旋量非负组合形成一个向量时不可能与超平面共面,也就不能形成超平面上的C,因此只可能是剩余的单位旋量对应的T中部分拉力为零.对于部分拉力为零的情况,可以作为工作空间的边界.同理,对于Stiemke引理时,一些剩余单位旋量位于超平面上,可考虑部分绳拉力为零,这样虽不满足式(19),但能使式(15)成立. 在特殊情况测试中,除了能形成法向量q,还需要计算剩余的单位旋量sgn,因此,对于Farkas引理,应满足m-n+1≥1,即m≥n.对于Stiemke引理,应满足m-n+1≥2,即m≥n+1.因此,当m≥n时,可以直接利用Farkas引理或者Stiemke引理.但是本文研究的欠约束时即m m=1或m=2时很难实现对被吊运物的控制,故主要研究的是m≥3且3 对于Stiemke引理的条件m≥n+1,部分情况下无法使用;同时也可以看出,当C=0时,使用的范围也有局限,适用于被吊运物的重力、惯性力等被其它外力平衡掉或者为零. 在仿真过程中,对于Farkas引理,可以给定被吊运物的位移加速度、角速度、角加速度的范围,再利用蒙特·卡罗方法随机产生被吊运物的位移加速度、角速度、角加速度具体值,这样C就已知了.动力学工作空间的仿真步骤如下: (1) 先通过已知条件判断是利用Farkas引理还是Stiemke引理,将动力学方程拆分成2部分. (2) 确定每个机器人的空间范围即Pm点的范围. (3) 通过机器人的空间范围确定被吊运物的位置r范围和姿态范围.对于Farkas引理,给定被吊运物的位移加速度、角速度、角加速度的范围. (4) 利用蒙特·卡罗方法随机循环N次,每次循环随机产生每个机器人的位置Pm、被吊运物的位姿和被吊运物的位移加速度、角速度、角加速度. (5) 在每次循环周期内,计算出每根绳长,并分别计算出拆分后的2组结构矩阵A,判断A是否发生降秩.如果发生降秩,本循环停止,进入下一循环.如果不发生降秩,则对试待测定的超平面进行判断,是否为分离超平面或者支撑超平面.如果是,则本循环停止,进入下一循环.如果不是,则重复测试,直到测试完该循环下的全部组合形式都不是分离超平面或者支撑超平面,同时拆分后的2组方程组应同时满足要求,否则本循环停止,进入下一循环. (6) 每次循环周期内,如果全部组合形式下都不是分离超平面或者支撑超平面,则此次循环内,被吊运物的质心位置属于动力学工作空间的点,记录下此时的空间坐标. (7) 重复步骤(5)和(6),直至N次循环完成,最后输出动力学工作空间的图形. 为了实验的方便性和安全性,以3台直角坐标机器人协同吊运6自由度被吊运物为实体实验平台,单个直角坐标机器人末端的工作空间范围为长方体.设直角坐标系机器人X、Y、Z方向的长度分别为 0.8、0.5 和 0.5 m.在地面上建立全局坐标系,每个机器人Z轴方向高度为 1.5 m. 3台机器人在全局坐标系中XOY平面摆放示意图如图2所示. 图2 3台机器人XOY平面示意图Fig.2 Schematic diagram of the XOY plane of the three robots 设被吊运物为一正三角形物体,三角形的顶点分别为B1、B2和B3,也是绳索与被吊运物的连接点,三角形中心到各顶点的距离d=0.1 m,被吊运物的质量M=10 kg.每个机器人末端点Pm的空间范围和初设的被吊运物质心O′的空间范围在全局坐标系中的表达式: (23) (24) (25) (26) 式中:被吊运物的姿态角范围为[0, 1] rad;被吊运物的X、Y、Z轴方向位移加速度范围都为[-1, 1] m/s2;被吊运物分别绕X、Y、Z轴转动的角加速度范围都为[0, 1] rad/s2;被吊运物分别绕X、Y、Z轴转动的角速度范围都为[0, 1] rad/s. 图3 被吊运物的动力学工作空间Fig.3 Dynamic workspace of the payload 按照第4.1节中的动力学工作空间的计算步骤,共循环1×105次,共得到 10 159 个满足要求的被吊运物的位置点.被吊运物动力学工作空间整体效果图如图3所示.该图是保证绳的拉力T≥0的工作空间,因此是包括部分绳的拉力为零作为边界的工作空间.动力学工作空间在XOY平面、YOZ平面以及XOZ平面的投影图如图4~6所示. 从图4的XOY平面可以看出,工作空间整体大致关于y=x的平面对称,且离原点越远越密集.从图5和图6可以看出,工作空间的下端比上端要密集些. 图4 XOY平面投影图Fig.4 XOY plane projection 图5 YOZ平面投影图Fig.5 YOZ plane projection 图6 XOZ平面投影图Fig.6 XOZ plane projection 在仿真中,确定了空间参数以后,还限定了角速度、角加速度和线性加速度的范围,但上述动力学工作空间的分析中并没有限制绳索的拉力范围,只是需要判断拉力的正负.故可推断:在确定的空间和结构参数条件下,被吊运物角加速度和线性加速度的范围的变化对动力学工作空间影响不大. 为了验证以上推论再做一组仿真,将上述的被吊运物的X、Y和Z轴方向位移加速度范围都变为[-5, 5] m/s2,被吊运物分别绕X、Y和Z轴转动的角加速度范围都变为[0, 2] rad/s2,被吊运物分别绕X、Y和Z轴转动的角速度范围都变为[0, 2] rad/s,其他参数都不变,这样C的范围发生了变化.同样,按照第4.1节中的动力学工作空间的仿真步骤,共循环1×105次,共得到 10 244 个满足要求的被吊运物的位置点. 分别对比2组仿真结果图,发现形状基本一样,满足要求的点的个数也相差不多.由于篇幅的限制,第2组仿真结果就不再图示.说明C的范围对动力学工作空间影响不大,这是因为动力学工作空间重点考虑的是保证绳的拉力T≥0,至于绳的拉力具体多大未予考虑,同时从测试步骤中sgn的计算也可以看出,重点只考虑了符号的正负和是否形成分离超平面或者支撑超平面,大小则无关.因此,C的范围只是影响绳的拉力值大小,而无法影响绳拉力的正负. 通过对欠约束多机协调吊运系统动力学工作空间的分析,得出以下结论: (1) 在动力学工作空间中,通过比较动力学方程与Farkas和Stiemke引理的关系,得出要使动力学工作空间的条件成立,就必须不能形成分离超平面或支撑超平面. (2) 在动力学工作空间中,当系统为欠约束时,无法直接使用Farkas和Stiemke引理来求解动力学工作空间,但对m≥3时,可以通过拆分动力学方程进行调整,最后能够得到动力学工作空间. (3) 通过对比不同被吊运物的加速度范围时的动力学工作空间仿真图,发现被吊运物的加速度对动力学工作空间影响不大.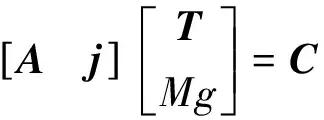
3 欠约束系统动力学工作空间求解
3.1 求解方法
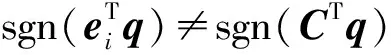
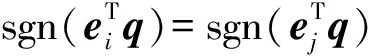
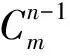
3.2 特殊情况分析
4 动力学工作空间计算分析
4.1 计算步骤
4.2 仿真结果分析
5 结论

