基于谱分析和裂纹扩展方法的舱口角隅疲劳寿命预报方法

余宏淦， 黄小平， 张永矿

(上海交通大学 高新船舶与深海开发装备协同创新中心， 上海 200240)

大开口船舶所具有的典型特征使得船体水平弯曲、扭转和横向强度在总强度中所占的比例明显上升，因此舱口角隅处会产生明显的应力集中[1].在交变应力和初始缺陷(如初始裂纹、夹渣、气缝等)的共同作用下，角隅自由边会萌生裂纹.裂纹可能会逐渐扩展至甲板及舷侧，进而导致整船的断裂，因此预报角隅的疲劳寿命十分必要.

然而，由于角隅受力较为复杂，起裂点不易确定，加之裂纹尖端附近存在的交变应力，要对角隅疲劳寿命进行准确评估是十分困难的.大开口船舶上甲板的主要应力成分有：静水弯矩、水平波浪弯矩、垂向波浪弯矩引起的正应力σ0；波浪转矩和横向力在抗扭箱断面产生的切应力τ；转矩导致不均匀的纵向变形而产生的翘曲正应力σω.这些应力在上甲板大致有如下的关系：σω/σ0可达 0.6～0.8；τ/σ0可达 0.2[2].可见，切应力和翘曲正应力在整个受力中占有较大的比重，这是大开口船舶所特有的，也是造成与上甲板相连的角隅受力复杂、应力集中严重的根本原因.对于同一角隅，不同工况下其结构响应不同，导致角隅自由边热点位置有变动，而裂纹往往在热点处产生.

目前，评估舱口角隅疲劳性能主要有许用应力范围法和谱分析评估方法.许用应力范围法，将角隅简化计算得到的应力范围同许用应力范围进行比较，以确定结构疲劳强度是否满足要求[3].谱分析评估方法，是由谱分析得到各海况下角隅应力范围分布并结合线性累积损伤原理及应力-寿命(S-N)曲线求得疲劳寿命.显然，许用应力范围法比较粗糙、保守且不能给出确切的疲劳寿命；谱分析评估方法中S-N曲线是否适用于高强钢尚需进一步讨论，且采用S-N曲线结合疲劳累积损伤原理校核疲劳寿命无法考虑载荷时程效应、预报结果离散度大、预报结果难以定量分析等问题.

Mao[4]采用谱分析结合断裂力学方法校核了甲板纵骨疲劳强度，由于舱口角隅结构和受力的复杂性，目前没有现成的应力强度因子(SIF)计算公式，阻碍了断裂力学方法在其疲劳校核过程中的应用.本文以某超大型集装箱船驾驶室前椭圆形角隅为例，开展谱分析方法结合断裂力学方法预报角隅疲劳寿命研究.首先通过水动力和结构响应分析得到全船响应；然后讨论角隅可能的起裂位置，并将全船分析结果作为 ANSYS 中建立的带裂纹角隅模型二次分析的边界条件；进而研究裂纹扩展路径并回归出相应的SIF经验公式，采用ABS船级社疲劳指南[5]推荐的谱分析方法生成疲劳载荷谱；最后结合Huang等[6-9]提出的单一曲线模型采用cycle-by-cycle 方法预报角隅疲劳寿命.

1 舱口角隅裂纹的扩展

1.1 船体结构响应分析

本文以某超大型集装箱船驾驶室前的椭圆形角隅为例对角隅的疲劳寿命进行预报，该集装箱船的主尺度如表1所示.通过直接有限元分析来研究角隅的疲劳问题，角隅及其附近的有限元模型如图1所示.

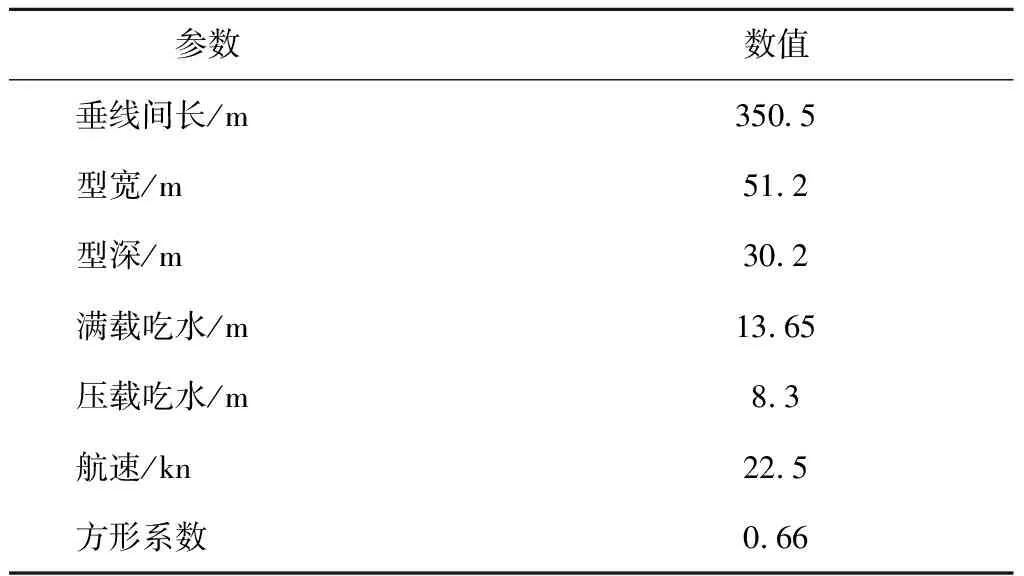
表1 某超大型集装箱船主尺度Tab.1 Principle dimensions of an ultra large container

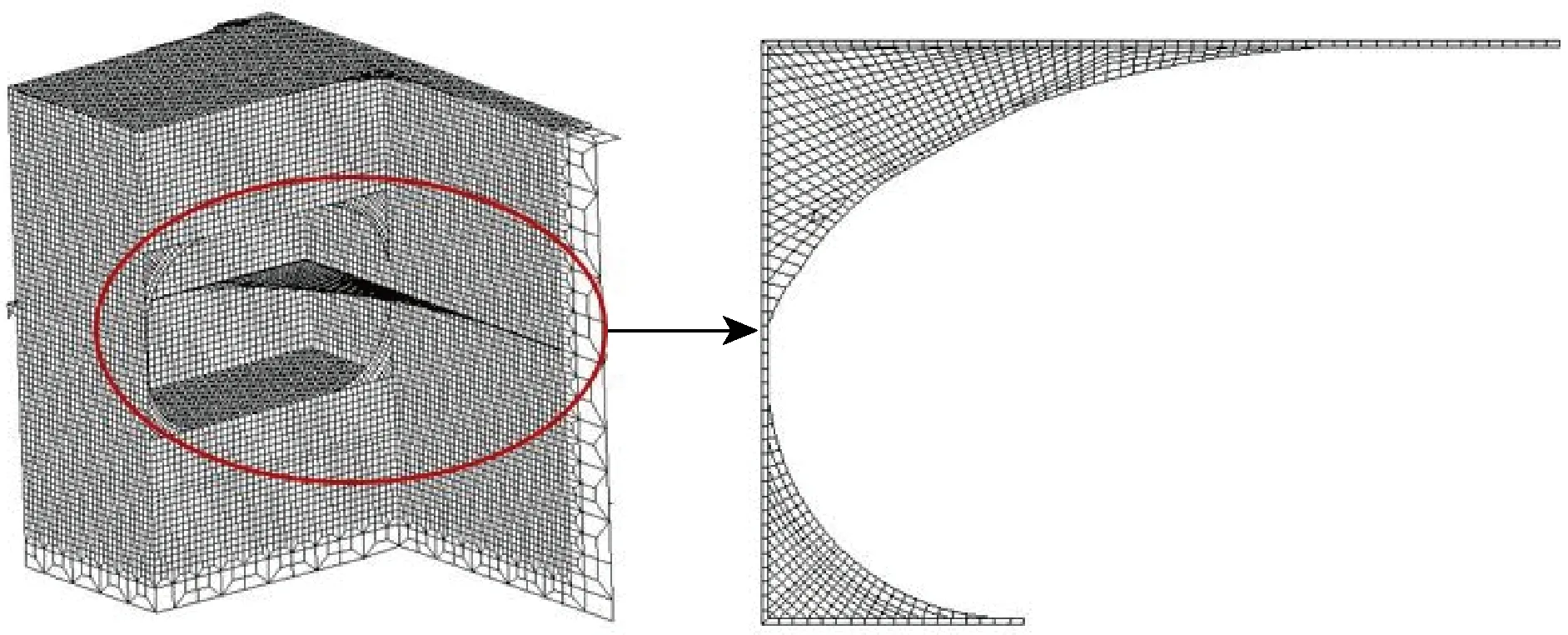
图1 舱口角隅Fig.1 Hatch corner

采用WALCS软件进行水动力分析，得到船体结构在满载单位波高条件下不同浪向和频率的运动和动力响应幅值算子RAOs.频率范围为 0.1～1.8 rad/s(步长 0.1 rad/s)，浪向范围为0°～330° (步长30°)，每个浪向等概率地出现，航速为设计航速的 2/3.将运动和动力响应加载到用Patran建立的全船有限元模型上，得到角隅的Von Mises应力，即可作为不同频率、浪向下的应力传递函数.

1.2 角隅起裂点范围的确定

不同浪向(θ)和频率(ω)下，船体结构响应会不同，导致角隅热点位置有变动，而裂纹往往在热点处产生.图2给出的是不同浪向(定义迎浪为180°)和频率下角隅的Von Mises应力云图.可见：热点沿自由边有变动；角隅靠近舷侧部分应力集中比较严重.由于材料和工艺等原因，角隅自由边可能会存在类裂纹缺陷，导致局部应力集中而产生裂纹.因此，角隅自由边起裂点的判定面临着实际困难，但是若不确定起裂点的位置则无法继续使用断裂力学方法.由于实际生产中角隅自由边会经过专门打磨以消除材料和工艺等引起的缺陷，故本文只考虑结构响应对起裂点位置的影响.文献[10]中根据DNV规范，采用设计波法得到椭圆形角隅的热点位置在靠近舷侧部分角隅的自由边中点；ABS规范[11]则指出，椭圆形角隅的热点位置在靠近舷侧部分角隅的自由边中点附近.萌生裂纹之前，角隅的热点位置有变动；萌生裂纹之后，热点只存在于裂尖处.由图2的应力云图可见，只需对靠近舷侧部分角隅建模进行分析.

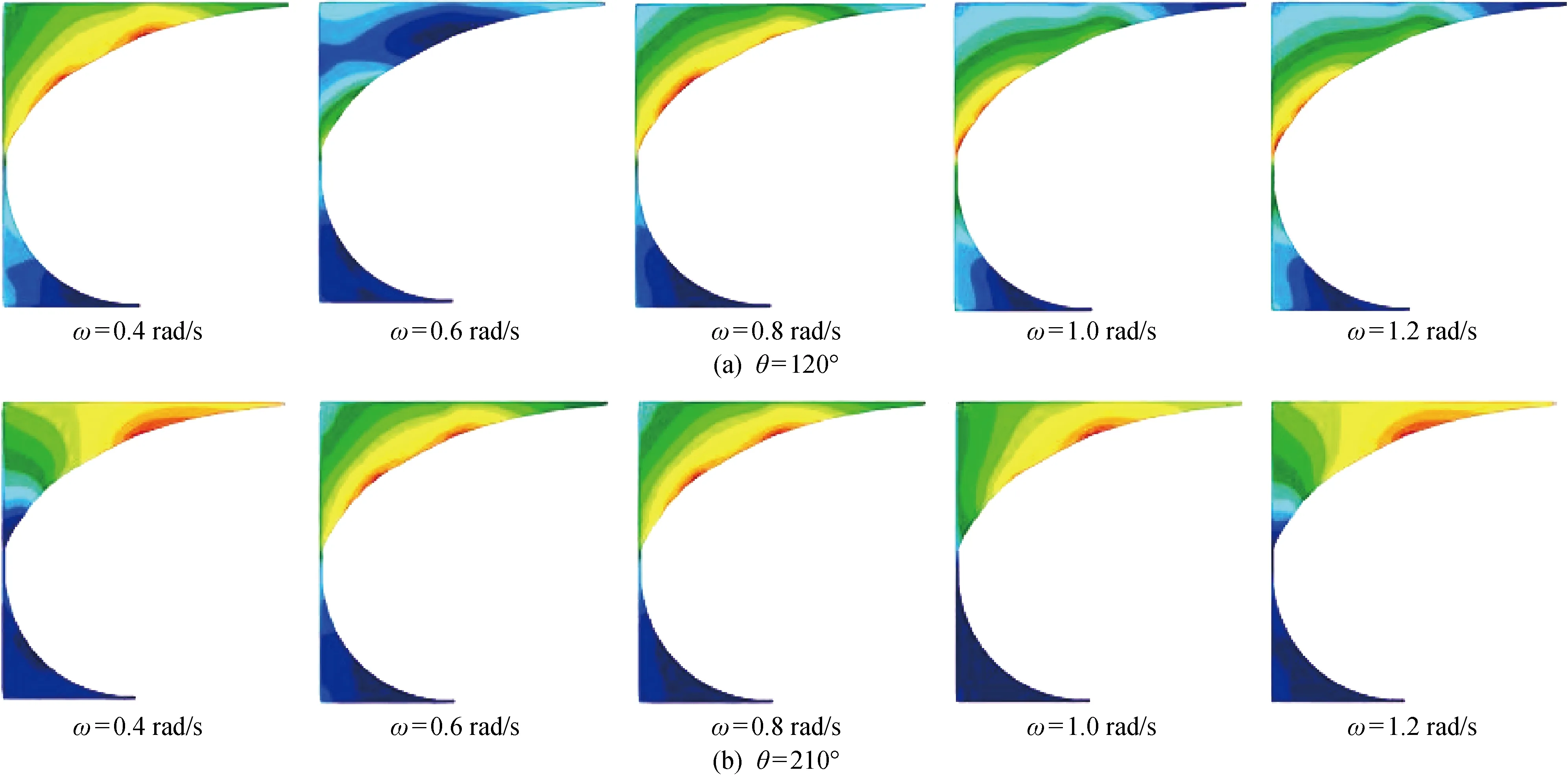
图2 不同频率和浪向下角隅Von Mises应力云图Fig.2 Von Mises stress contour of hatch corner in different frequencies and directions

1.3 step-by-step计算裂纹扩展

采用step-by-step方法计算裂纹扩展路径.首先，在起裂点处预制一个初始裂纹并指定扩展步长，然后计算裂纹的SIF或应变能；接着，通过相应的准则判断裂纹的扩展角并结合扩展步长预报下一个裂尖位置.如此反复，得到裂纹扩展路径.

1.3.1验证实例 通过Sumi等[12]所做的裂纹扩展实验数据来验证编写的模拟裂纹扩展程序的精确性和稳定性.图3给出了试件部分几何尺寸和外部载荷条件.图中：H为腹板高度；W为试件颈部宽度；P为交变载荷，分为Pmin和Pmax；G为试件下部分宽度；tw为上部分板材厚度；tf为下部分板材厚度.试件中表征初始裂纹的切口(长度5 mm)位于受到双轴应力的纵横构件的交接点处，分为横向切口试件和纵向切口试件.试件下部两端简支，上部受交变拉伸载荷作用，上下部件焊接在一起，通过改变下部构件的弯曲刚度和上部构件中间部分的宽度可以使切口处获得不同的双轴应力.表2给出了试件更详细的几何尺寸和载荷条件，试件所用材料为船用KA36钢.

模拟的A系列试件的裂纹扩展路径如图4所示.由图4可见：对于A1，本文的模拟结果与实验结果更为吻合；对于A3，本文的模拟结果及Sumi的模拟结果与实验结果相比开始很吻合，后来有偏差.模拟的B系列试件的裂纹扩展路径如图5所示.由图5可见：本文模拟结果与实验结果更为吻合.因此，所编写的预测裂纹扩展路径的程序具有相当的精确性与稳定性.

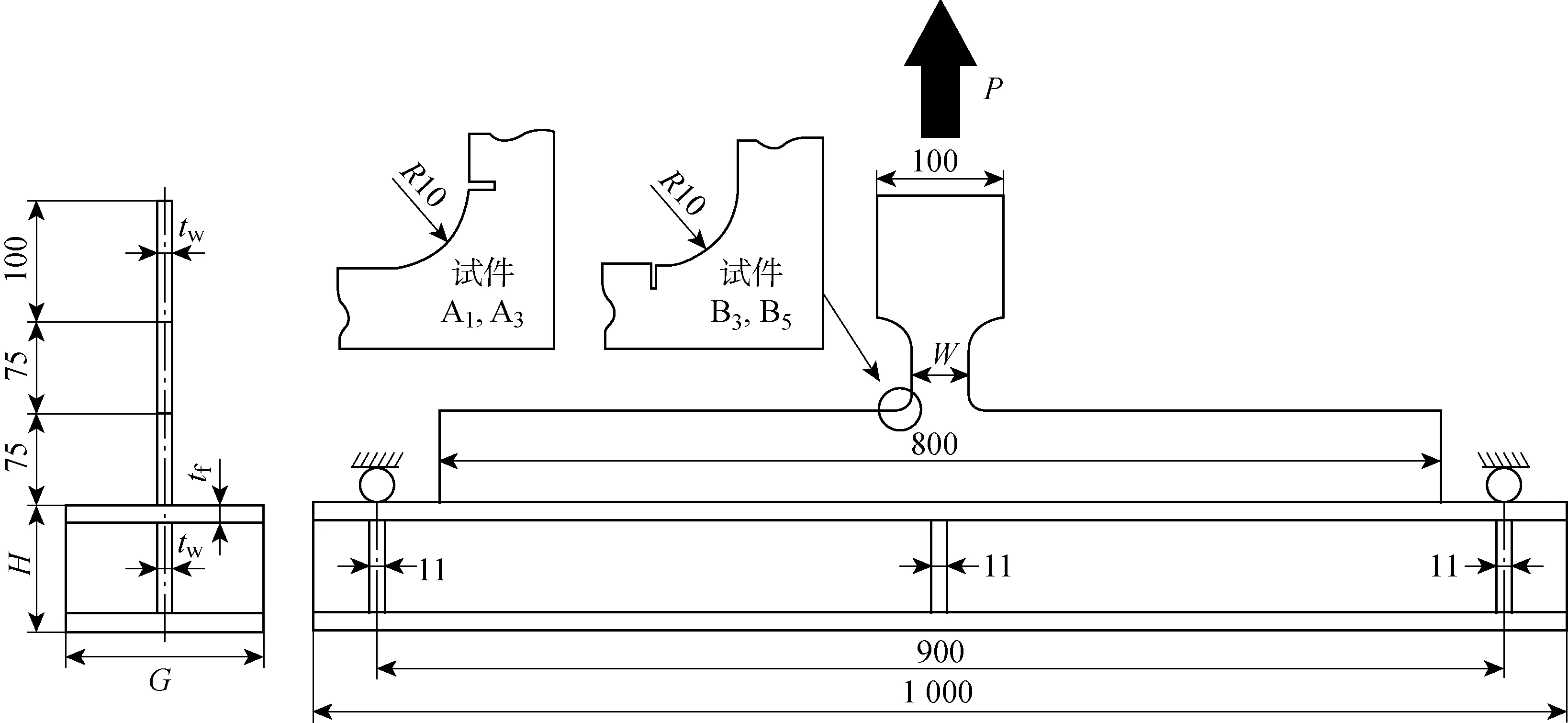
图3 试件的几何尺寸及载荷条件(mm)[12]Fig.3 Geometry and loading condition of the specimen (mm)[12]

表2 试件的几何尺寸和载荷条件[12]Tab.2 Geometry, loading conditions of the specimens[12]

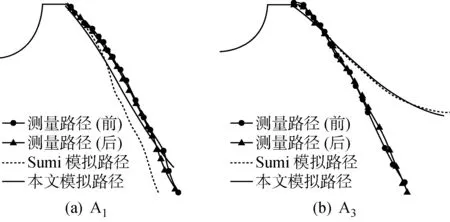
图4 试件A1与A3测量和模拟的裂纹扩展路径Fig.4 Measured and simulated paths of cracks of specimens A1 and A3

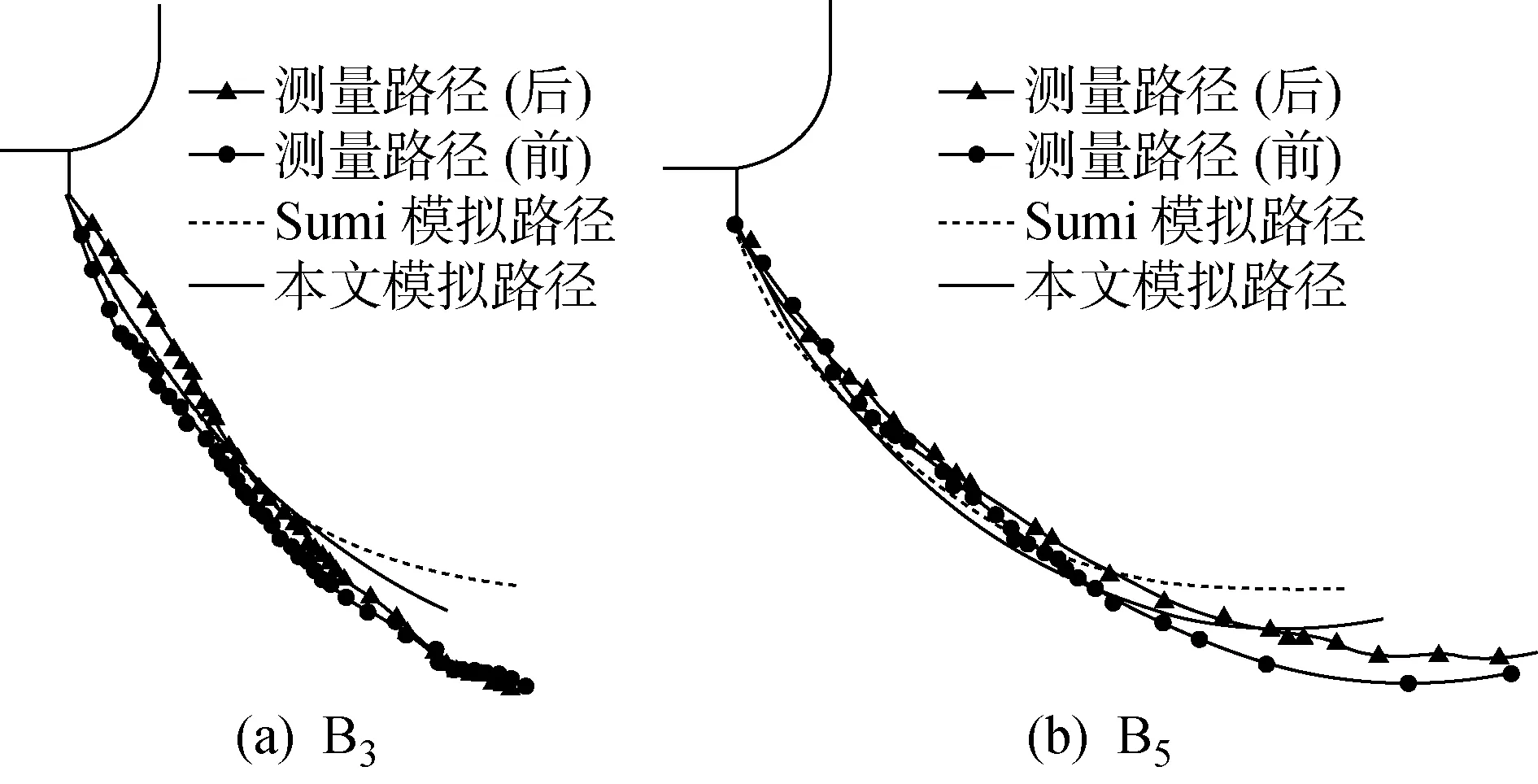
图5 试件B3与B5测量和模拟的裂纹扩展路径Fig.5 Measured and simulated paths of cracks of specimens B3 and B5

1.3.2角隅扩展路径计算 根据1.2节的分析，在角隅的中点附近选择5个起裂点，如图6中点①～⑤所示，基本覆盖了可能产生裂纹的自由边.首先，从Patran中将经过全船结构响应分析的目标角隅附近模型导入ANSYS，求解生成超单元(super-element)(见图7(a)).然后，在ANSYS中建立带裂纹目标角隅模型(见图7(b))，并与超单元耦合，将全船分析结果作为带裂纹角隅模型二次分析的位移边界条件(见图7(c)).最后，求得角隅裂尖在单位规则波不同频率和浪向下的应力强度因子KI和KII，根据有关准则判断裂纹的扩展(见图7(d)).超单元作为ANSYS的有力工具，可以减小系统自由度，在step-by-step计算裂纹扩展时，每次迭代只需要引用超单元的质量和刚度矩阵等参数，无需大量重复计算，极大地缩短了计算时间，使计算量庞大的问题在有限的计算机资源下能顺利求解.

复合裂纹的扩展角主要有以下3种判定准则：最大周向应力准则(MCSC)[13]，最小应变能密度准则(MSEDC)[14]以及最大应变能释放率准则(MSERRC)[15].Bittencourt等[16]证明了这3种判定准则的数值计算结果基本一致，本文选择MCSC来判断裂纹的扩展方向.

各起裂点萌生的裂纹在不同频率和浪向下的扩展路径如图8所示(程序进行裂纹扩展计算时将裂纹终止长度设为200 mm).可见：裂纹扩展初期(<120 mm)其路径基本一致且垂直于起裂点处自由边的切线，随后逐渐分散.

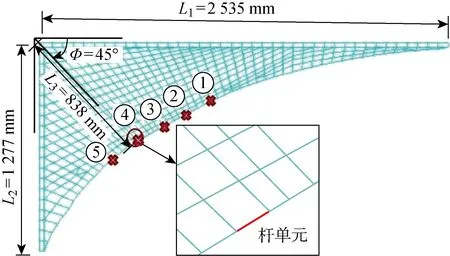
图6 舱口角隅几何尺寸及起裂点位置Fig.6 Geometry and positions of crack initiation points of the hatch corner

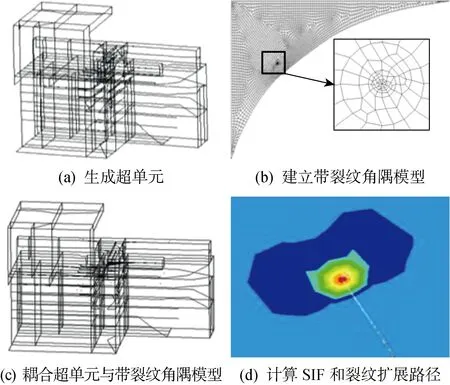
图7 建模及计算过程Fig.7 Modeling and calculation process

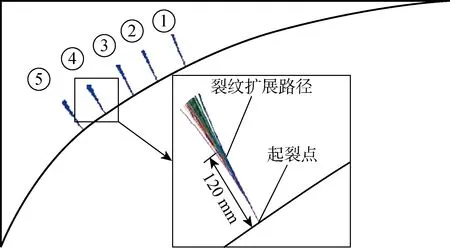
图8 舱口角隅裂纹扩展路径Fig.8 Crack propagation paths of the hatch corner

进而可以推知，角隅实际的裂纹扩展路径会在初期垂直于起裂点处自由边切线.

1.4 角隅SIF计算公式

不同浪向和频率下，SIF随裂纹长度变化的曲线组离散度很大，其本质原因是裂尖附近具有不同的应力场.为回归出角隅统一的SIF计算公式，需研究SIF与应力场的关系，以消除应力场差异对公式回归的影响，同时由谱分析生成载荷谱时也需要提取应力场中合适的应力.因此，接下来先提取应力场中合适的应力，然后研究SIF与该应力的关系，以回归出统一的角隅SIF经验公式.

1.4.1应力传递函数 角隅的几何特点，决定了其不具有单边裂纹SIF计算公式中那样的远场应力，因此本文考虑提取角隅应力场中合适的应力作为参考应力.但是，角隅结构响应十分复杂，裂纹扩展时应力场在不断地变化，这给合理地提取参考应力带来困难.影响裂纹扩展的主要应力是起裂点处沿角隅自由边的切向应力，与已经很成熟的谱分析评估方法中提取应力传递函数一致，此处提取单位波高不同浪向和频率下起裂点处虚设杆单元(见图6)的轴向应力[17]，即角隅自由边的切向应力，作为应力传递函数.

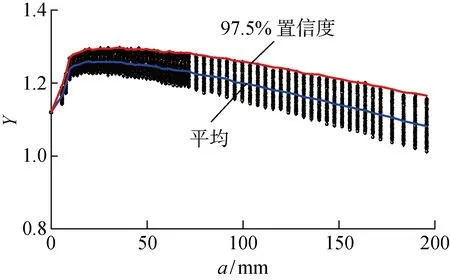
图9 起裂点①的几何修正因子Fig.9 Geometric correction factor of crack initiation point ①

1.4.2几何修正因子 由于角隅裂纹为单边裂纹，其SIF计算公式可统一写成

(1)

式中：K为SIF；σ为应力；Y为SIF几何修正因子；a为裂纹尺寸.将直接有限元分析得到的K和提取的传递函数σ一起代入式(1)，可以求得不同频率和浪向下的Y.图9所示为不同浪向和频率下起裂点①处裂纹扩展过程中Y的变化情况(其余起裂点的Y与图9类似，不再一一给出，但各点Y的处理结果将在图10中汇总).由图9可见：Y先上升后下降且离散度不大，特别是在裂纹扩展初期，最大值不超过 1.3.几何修正因子有短暂的上升是因为SIF在裂纹扩展初期迅速增大，而之后的下降则是由载荷流泻所致，实验和理论分析都证实载荷流泻会减缓SIF增长速率.图10所示是对5个起裂点2条曲线(平均和 97.5% 置信度)数据的汇总.由图10可见：Y总体很接近，起裂点⑤的Y值后期数据偏小(可能受靠近纵中剖面部分角隅的影响)；5个起裂点下Y总体在依次减小；有限板宽边裂纹几何修正因子公式不适用于角隅SIF计算.保守起见，此处选择起裂点①下2条曲线对应的Y作为整个角隅SIF的几何修正因子，如图11所示，并由2条曲线的数据分别拟合出与边裂纹几何修正因子公式相近的公式：

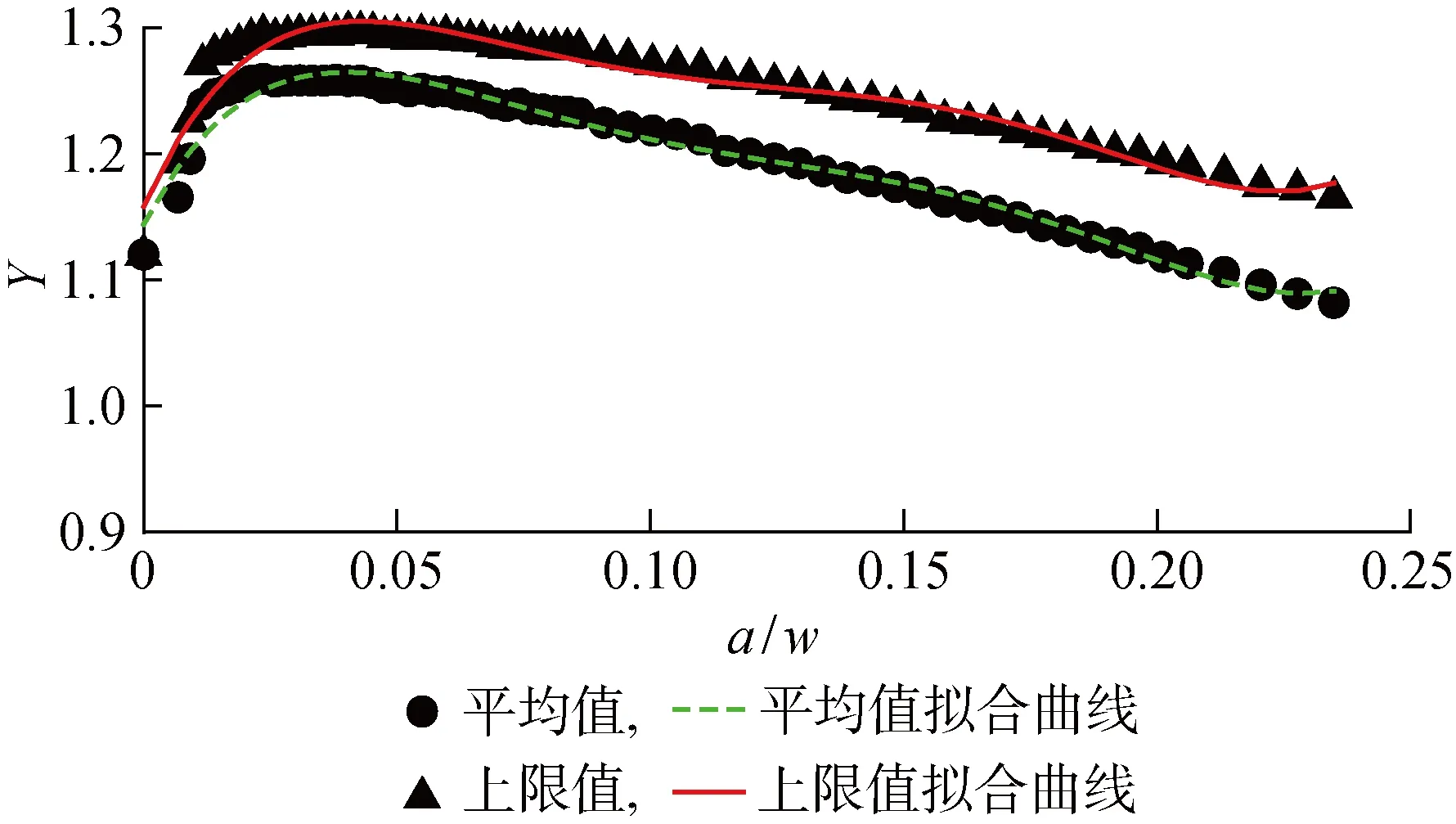
图11 Y曲线拟合Fig.11 Curve fitting of Y

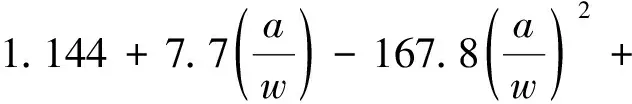
(2)

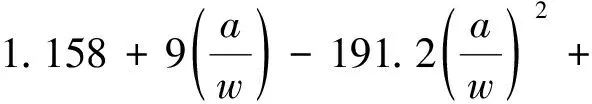
(3)

式中：w为角隅直角顶点与自由边的最小距离(见图6中L3).式(3)相对于式(2)较为保守.

2 舱口角隅寿命评估

2.1 谱分析法生成疲劳载荷谱

采用ABS[5]推荐的谱分析方法生成疲劳载荷谱.首先选择合适的海浪散布图，采用ISSC (International Ship Structure Congress)推荐的双参数P-M谱:

Sη(ω|HS,TZ)=

(4)

然后由下式得到应力能量谱Sσ(ω|HS,TZ,θ):

Sσ(ω|HS,TZ,θ)=

|Hσ(ω|θ)|2Sη(ω|HS,TZ)

(5)

接着考虑短峰波效应后由下式得到n阶谱矩mn:

(6)

最后由谱矩得到短期海况服从Rayleigh分布的应力：

(7)

0≤Δσ≤+∞

式中：HS为有义波高；TZ为平均跨零周期；ω为角频率；Hσ(ω|θ)为线性动力系统幅频响应函数；θ为浪向角(定义180°为迎浪)；α为考虑短峰波效应后的浪向角；g为重力加速度；V为2/3设计航速；Δσ为应力范围.

不同于传统的S-N曲线方法预报疲劳寿命，采用断裂力学方法需要在已知应力范围概率密度的基础上构造疲劳载荷谱.文献[19]中讨论了2种构造疲劳载荷谱的方法，分别是将服从Rayleigh分布的短期载荷谱叠加得到长期载荷谱上以及在前者的基础上拟合得到服从Weibull分布的疲劳载荷谱.尽管两种方法的差别不大，但是前者更为直接和方便，这里选择前一种方法.

2.2 裂纹扩展模型

裂纹扩展模型选择Huang等[6-9]提出的单一曲线模型.这是一个由裂纹扩展率单一曲线和相应的等效应力强度因子幅组成的裂纹扩展预报模型，其基本表达式为

式中：ΔKeq0和ΔKth0分别为应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值；C为Paris系数；m为裂纹扩展指数；MR为载荷比的修正因子；MP为载荷次序的修正因子；K为应力强度因子.

用cycle-by-cycle方法计算疲劳寿命，需要知道初始裂纹尺寸和临界裂纹尺寸，初始裂纹尺寸由规范或者实际测量给出，临界裂纹尺寸这里借助BS7910标准[18]推荐的失效评估图(FAD)Level 2A来判定.

2.3 角隅寿命计算

由2.1节介绍的方法生成疲劳载荷谱.将载荷谱和几何修正因子(式(2)或式(3))代入式(1)得到应力强度因子计算公式，再结合2.2节介绍的单一曲线模型和失效评估图，即可预报角隅的疲劳寿命.目标角隅材料为E40钢，具体参数如表3所示，设计寿命20 a.为了计算角隅裂纹扩展寿命，此处取角隅初始裂纹尺寸为 0.5 mm.表4所示为北大西洋海浪散布图下，初始裂纹尺寸为 0.5 mm，角隅各起裂点下裂纹扩展寿命(N)计算结果.可见：式(3)比式(2)保守，但两者预报寿命很接近，相差不超过10%.图12所示为采用式(2)时，5个起裂点相应的裂纹扩展曲线. 另外，由失效评估图算得，角隅在不同起裂点下的临界裂纹尺寸在32 mm附近，对照图8可知，此时的裂纹扩展路径垂直于起裂点处的自由边切向.

表3 E40钢材料参数Tab.3 Material parameters of steel E40

表4 各起裂点裂纹扩展寿命Tab.4 Crack propagation life of each crack initiation point

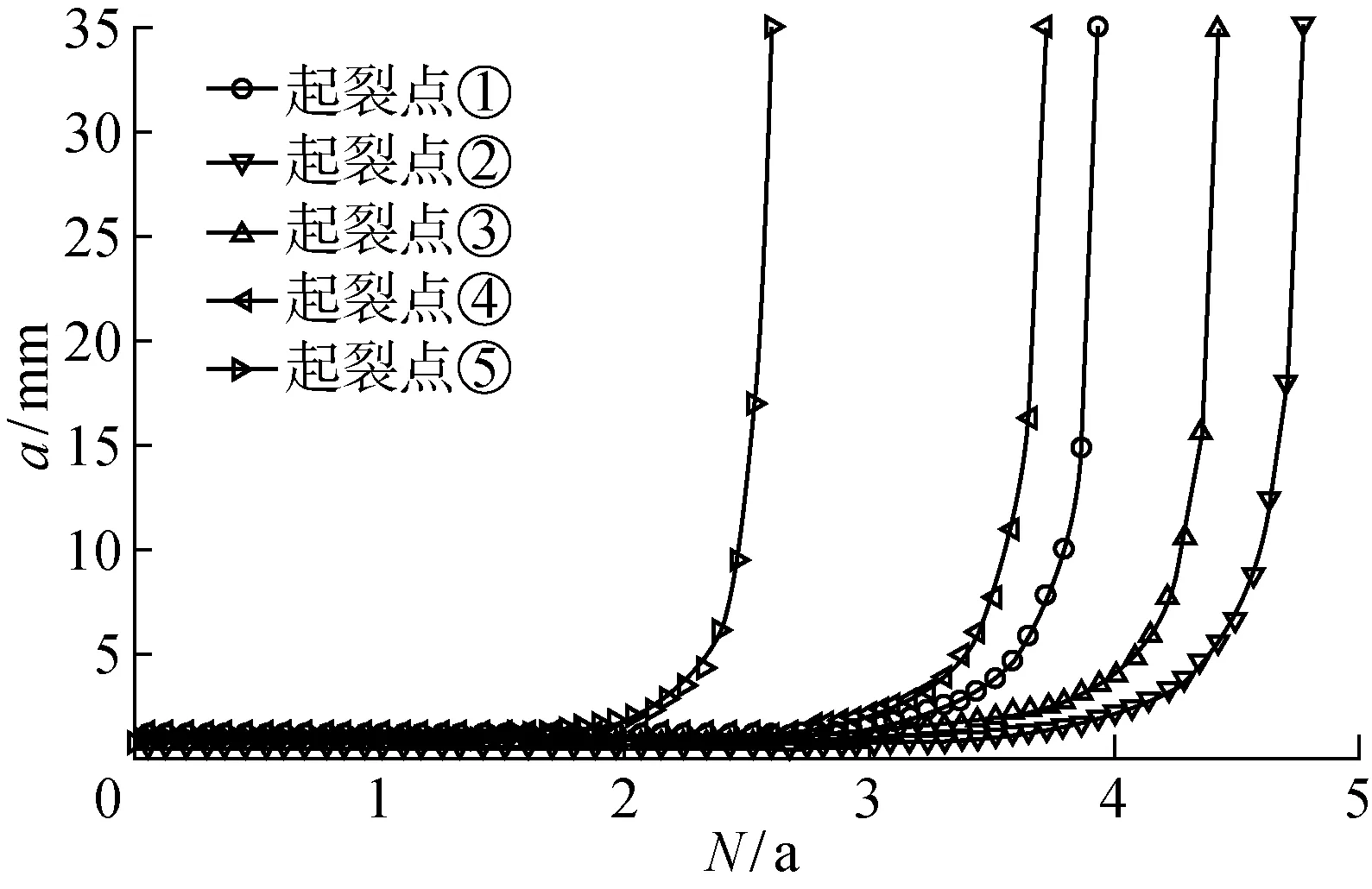
图12 裂纹扩展曲线Fig.12 Crack propagation curves

3 结论

本文重点研究了某超大型集装箱船驾驶室前椭圆形角隅在不同外载荷、不同起裂点下的扩展问题.通过谱分析生成载荷谱，采用断裂力学方法计算应力强度因子，进而预报角隅裂纹扩展寿命.研究得到结论如下：

(1) 椭圆形角隅热点位于靠近舷侧部分角隅自由边.

(2) 不同工况下，角隅裂纹扩展路径初期基本一致且垂直于起裂点处自由边切线方向，后来逐渐分叉.

(3) 不同工况下，SIF几何修正因子Y随着角隅裂纹的扩展先上升后下降；有限板宽边裂纹SIF计算公式并不适用于计算角隅裂纹的SIF；拟合出Y的计算公式，再结合式(1)便可得到该角隅统一的SIF计算公式.

(4) 关于角隅初始裂纹尺寸的研究尚少，有待进一步深入研究；拟合公式式(3)比式 (2)保守，但两者预报寿命相差不大.