基于混合引导策略的高精度萤火虫优化粒子滤波算法
毕晓君, 胡菘益
(哈尔滨工程大学 信息与通信工程学院, 哈尔滨 150001)
粒子滤波(PF)作为一种处理非线性、非高斯动态模型估计问题的有效方法[1],已广泛用于航迹重构、目标跟踪、工业控制以及故障诊断等领域,但其重采样阶段破坏了粒子多样性[2-3],从而影响了滤波精度,尤其是在样本数受限的情况下[4],为此,国内外学者提出了一些改进方案.其中,群智能优化算法具有良好的寻优特性,它利用种群迭代来寻优取代粒子滤波重采样,避免了对粒子的盲目取舍,可以获得更加合理的粒子分布,从根本上解决了粒子多样性较差的问题,已成为现代粒子滤波技术发展的一个新的研究方向[5-6].文献[7]中采用自适应粒子群优化的粒子滤波(PSO-PF)算法,自适应动态控制邻域粒子的数量,避免了粒子早熟并提高了滤波效率;文献[8]中提出基于遗传算法(GA)的改进粒子滤波模型(GA-PF),利用种群最差数据与种群特殊数据进行交叉变异修正,以增强粒子多样性;文献[9]中提出差分进化与粒子滤波融合的算法(IDE-PF),通过融合适应度函数,引导粒子向后验概率密度较大的位置移动,从而扩展了粒子的分布范围以及提高了滤波精度;另外,文献[6]中将萤火虫算法(FA)用于改进粒子滤波,引入全局最优值来引导粒子群的整体运动,从而增强了算法的全局搜索能力,因其易于工程实现而被广泛关注.但是,基于智能优化思想的改进粒子滤波算法仍然存在搜索策略盲目的问题,而且过分注重粒子探索能力,未能很好地权衡粒子寻优后期的开发能力,影响了粒子向高似然区域移动的效率;同时,迭代寻优过程中存在失效个体,增加了算法的计算冗余度,而且用于引导种群寻优的可信度标准过于单一并依赖于粒子权重,由此而产生了质量较差的寻优粒子,虽然克服了粒子多样性较差的问题,但其滤波精度还有待于提高.
针对上述问题,本文提出了基于混合引导策略的萤火虫优化粒子滤波(MSFA-PF)算法,从而提高了滤波精度以及滤波效率.
1 粒子滤波
粒子滤波(PF)是采用蒙特卡罗随机采样方法对后验概率密度函数p(xk|zx)进行近似处理,以获得最小方差的状态估计[10].假设非线性回归滤波模型的状态方程和观测方程分别为
xk=f(xk-1,uk-1)
(1)
zk=h(xk,nk)
(2)
式中:xk为k时刻的状态值;zk为k时刻的测量值;f为状态转移函数;h为量测函数;uk和nk分别为k时刻的系统噪声和量测噪声.以下为采用PF方法处理非线性动态估计问题的步骤.
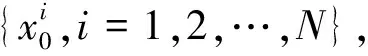
步骤2序贯重要性采样.具体方法:
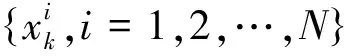
(3)
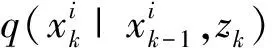
(2) 根据序贯重要性采样,所得更新的粒子权值为
(4)
当粒子分布存在贝叶斯滤波理论丢失的情况时,将粒子权重进行补偿及更新[11-12]:
(5)
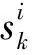
(6)
步骤3重采样.通过判别有效采样尺度来决定是否执行重采样,其判别公式为
(7)
式中:Neff为有效粒子数;Nth为重采样门限值.
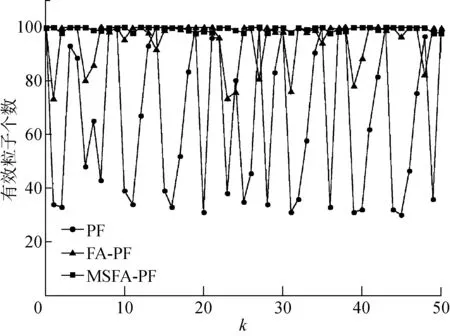
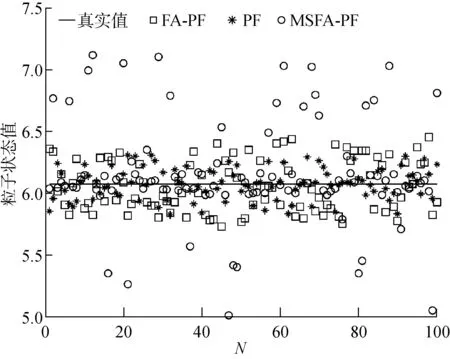
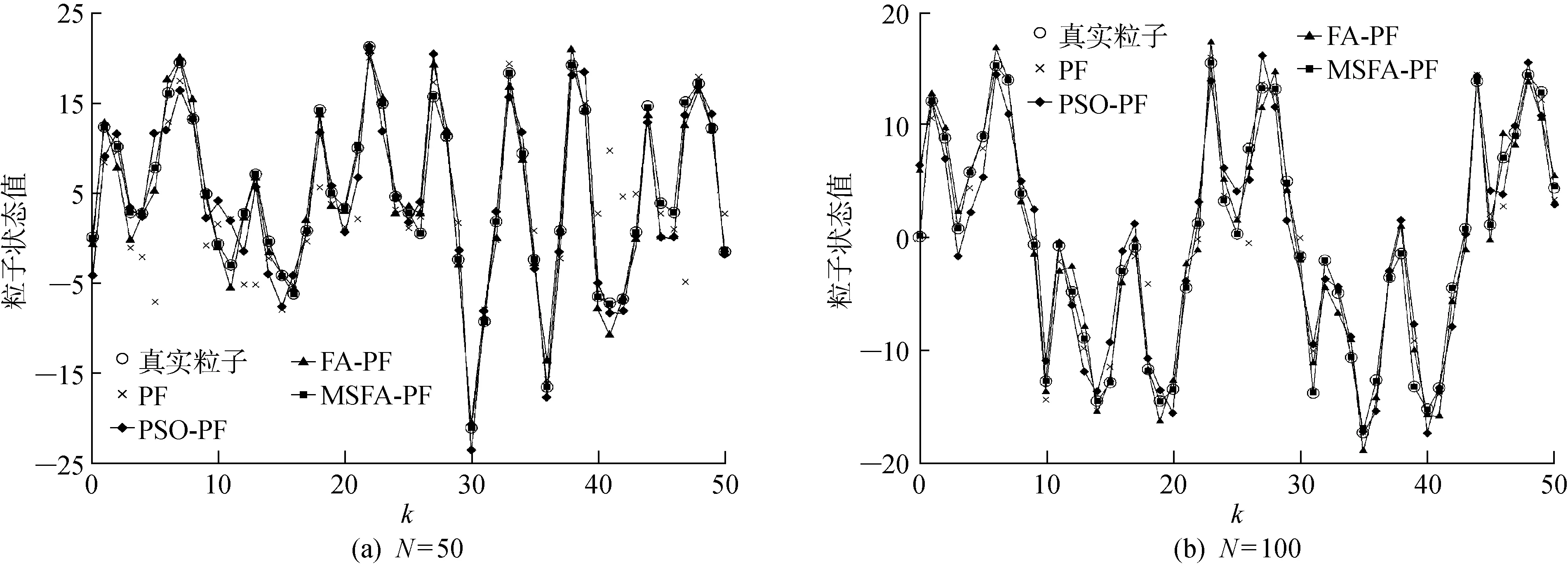
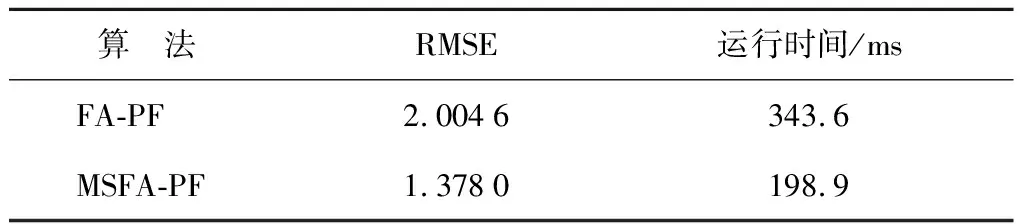
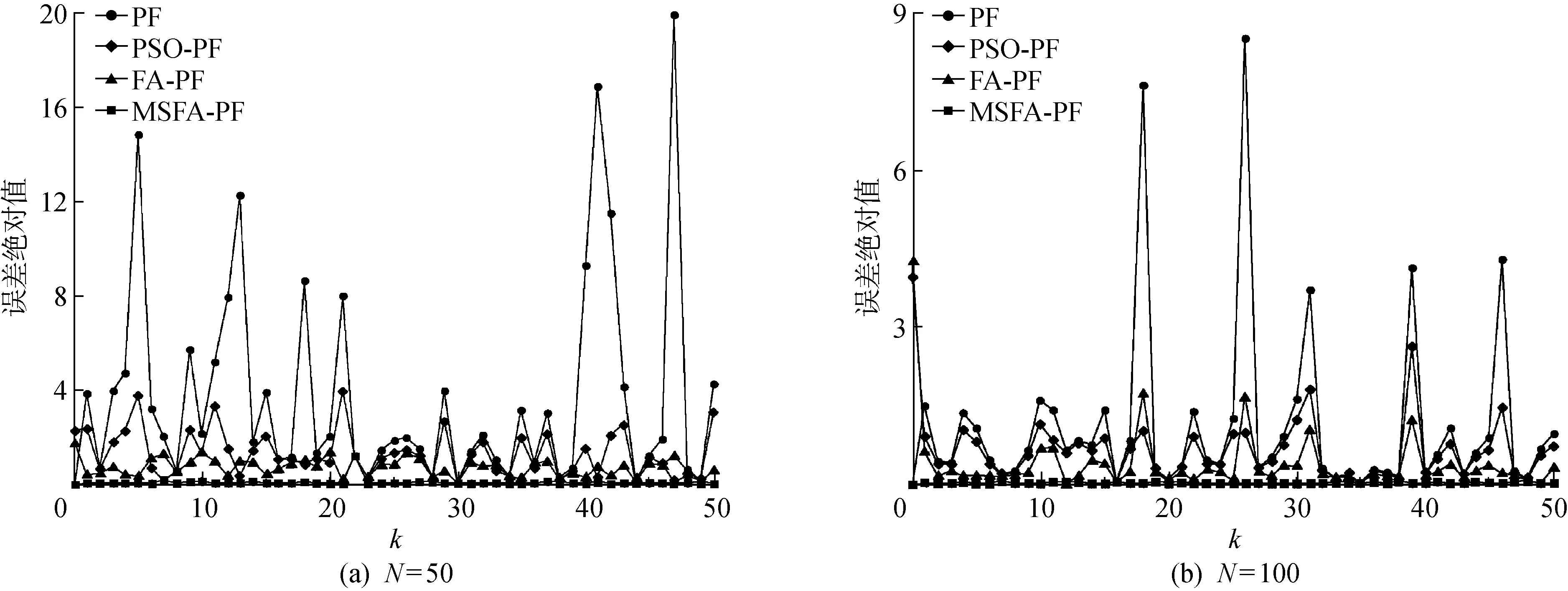
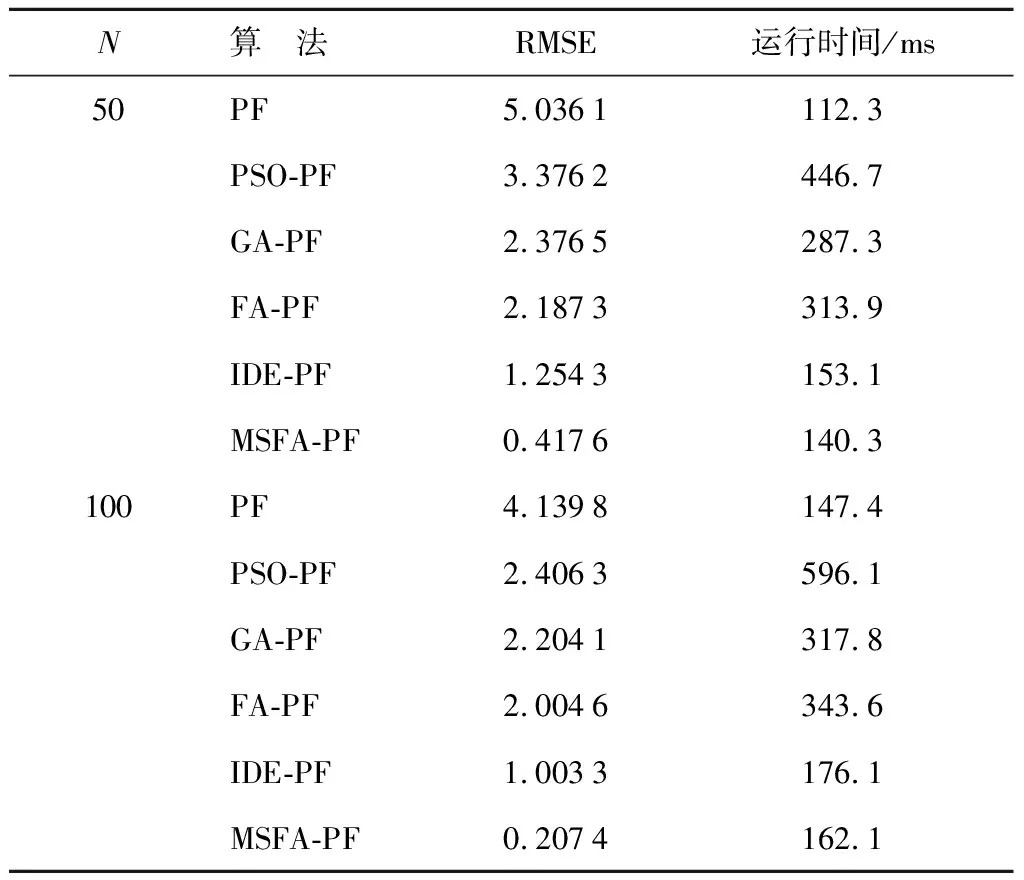
如果Neff 步骤4状态估计输出.采用粒子集近似方法计算k时刻的系统状态估计值,即 (8) 步骤5令k→k+1,当下一时刻测量值到来时,执行步骤2. 虽然文献[6]中利用萤火虫优化的思想改进了粒子滤波算法,但其仍存在算法时效性差以及滤波精度低的问题,本文通过研究找出了其根本原因,并从3个方面进行改进,提出了MSFA-PF算法. 群智能优化粒子滤波算法时效性差的根本原因在于搜索策略盲目,过分注重算法的探索能力,而如果为了提高算法寻优速度而牺牲算法探索能力,则将增大算法陷入局部最优的概率.为此,本文提出一种自适应作用于不同寻优阶段的均衡搜索方法,即混沌扰动搜索策略. 根据混沌理论,当混沌变量映射至相空间时,其遍历搜索方式能够有效处理算法前期粒子分布相对分散以及算法后期粒子分布相对集中的寻优问题,且比一般的随机搜索方式的全局搜索能力更强[13].本文以混沌扰动搜索代替标准FA算法中的随机扰动搜索,对粒子的吸引搜索进行引导,并考虑到传统的Logistic方法在映射空间内存在断点且映射点在空间内分布不均的问题,采用适用性较强且快速的Tent映射生成混沌变量[14],其模型方程为 (9) 式中:zk为混沌变量. 将Tent映射混沌变量引入扰动项,对粒子位置进行遍历搜索扰动.改进的位置更新为 (10) 在迭代初期,希望对萤火虫种群个体进行较大扰动,以增强探索能力而有利于跳出局部极值点,因此,要求ηk的取值较大;而在搜索后期,要求对个体减小扰动,以提高算法的开发能力,故ηk的取值应尽量小.为此,本文设计如下自适应调节系数: (11) 式中:α为步长因子;s为当前迭代次数. 对上述混沌扰动策略进行分析,通过引入荧光亮度的最大值来引导粒子群整体运动,以降低交互运算产生的运算复杂度.而混沌扰动项能够平衡粒子个体吸引及其移动过程中的搜索能力.在随机状态空间搜索寻优初期,粒子群相对分散,周边存在较多局部极值,需通过较大的混沌扰动来提高算法探索能力,以保证粒子获得最宽广的分布,避免了算法前期陷入局部最优解;在搜索寻优后期,粒子相对移动至全局最优值周围,此时的位置扰动不宜过大,通过自适应调节系数来减小混沌扰动,在保证算法开发能力的同时提高了算法的收敛速度.总体来看,算法在迭代过程中能够有效平衡搜索策略,以获得极强的全局搜索能力,促使粒子高效地向高似然区域移动,从而提高了滤波效率. 萤火虫的吸引度可视为粒子个体的视觉搜索范围.在搜索初期,粒子随机分布在状态空间中,且其相对疏散,在种群数目受限的条件下粒子分布空间存在边缘个体,因其距离种群目标个体较远,未能获取其他个体的有效亮度传递信息,故使其在初始位置无效波动,最终成为失去寻优功能的失效粒子,导致滤波的精度以及效率降低.为此,本文对吸引度计算公式进行如下改进: (12) 式中:β0为最大吸引度;γ为光强吸收系数;rij为萤火虫i与j之间的空间距离;v为动态视觉权重.v值越小,粒子寻优的视野越宽阔,越容易获取距离较远位置的有效亮度传递信息;而v值越大,粒子可视范围越小,搜索精度越高. 在FA-PF算法中,希望算法初期的粒子个体具有较大的视野范围,以使得粒子获取有效亮度信息的可能性增大;同时,希望在算法后期,当种群个体粒子之间距离相对变小时,能够对周边亮度信息进行精确定位.因此,本文设计了如下动态视觉权重: (13) 式中:ξ∈[2,3],为可视系数;Smax为最大迭代次数;S为当前迭代次数. 在吸引度计算公式中引入视觉搜索策略,能够动态控制萤火虫个体的视觉范围,在种群相对分散的寻优初期,利用较小的视觉权重来获得萤火虫个体的广阔视野空间,使其高效地向高似然区域移动,从而降低种群边缘个体陷入局部极值,并有效提高滤波粒子的利用率;在算法后期,随着迭代次数增加,种群个体相对聚集在最优目标周围,此时,过大的可视范围将造成寻优资源浪费并且增加运算时间,因算法可视距离权值随迭代次数增大而增大,所以采用动态减小搜索视野的方法,使得个体高度集中至最亮萤火虫周围,即全局最优区域,从而大幅提高算法的滤波效率以及精度. 可信度标准可用于衡量粒子携带的有效信息对滤波的贡献能力.由文献[6]中可以看出,FA-PF算法的适应度函数过于依赖似然度的量测误差[6],仅利用权重作为可信度标准,破坏了在高似然区域粒子集优化的完整度,即粒子权值的分布特性,致使粒子在算法后期的多样性不佳,从而影响滤波精度.荧光亮度表征了粒子个体的目标优劣程度,决定了粒子的移动方向,故将可信度标准扩展至荧光亮度.本文对荧光亮度计算公式进行改进,所得改进的荧光亮度为 (14) 通过上述改进,本文MSFA-PF算法流程如下: (1) 设定所需参数,包括粒子数N、最大吸引度β0、步长因子α、光强吸收系数γ和最大迭代次数Smax. (4) 模拟萤火虫优化方法的吸引和移动行为.首先,对粒子采用动态视觉搜索策略(式(12))获取粒子吸引度;然后,采用混沌扰动搜索策略(式(10))更新粒子位置,迭代拟合最小方差估计. (5) 判断拟合终止.本文设置迭代终止阈值ε=0.02,当荧光亮度函数值大于ε时,停止算法迭代,否则,继续迭代至最大迭代次数;当算法符合设定的ε值时,粒子已收敛至粒子真实值,或达到最大迭代次数,此时停止优化;否则转入(4). (6) 利用拟合获得的粒子分布,采用式(5)对粒子权重进行补偿及更新. (7) 采用式(6)对补偿更新的粒子权重进行归一化. (8) 将归一化粒子权重代入式(8)计算滤波状态估计值并输出. 为了验证所提出的MSFA-PF算法的有效性和新颖性,本文进行了仿真实验.实验的硬件环境为英特尔core i7-5700HQ处理器、16 GB内存,软件环境为MATLAB 2010b.实验引用单变量非静态增长模型[6]进行验证,它具有高度非线性,且其似然函数呈双峰状.其中,状态模型和量测模型如下: 8cos[1.2(k-1)]+uk (15) (16) 式中:uk和nk均为噪声. 实验所用滤波时间步长t=50.在萤火虫算法中,可视范围圆心处的最大吸引度一般设定为[0.8,1.0]区间内的常数,步长因子α一般取[0,1]之间的常数,因此,本文设置最大吸引度β0=0.9,α=0.5,γ=1,Smax=300. 验证滤波精度的指标为均方根误差[2],即 (17) 将与具有代表性的现有算法PF、PSO-PF[7]、GA-PF[8]、IDE-PF[9]以及FA-PF[6]与本文提出的MSFA-PF算法进行仿真实验对比.在PSO-PF算法中,设置学习因子C1=C2=2,惯性权重呈线性递减,其最大值为 0.9,最小值为 0.3;在GA-PF算法中,交叉概率Pc=0.5,变异概率Pm=0.001,变异自适应系数A=9.903;在IDE-PF算法中,微分进化算法的交叉概率PCR=0.9,优化迭代结束阈值σmin=0.001;在FA-PF算法中,其参数的设定与本文提出的MSFA-PF算法的一致. 本文从3个方面对算法进行了改进.首先,验证3个改进策略的改进效果.因篇幅有限,本文选取粒子数N=100对算法的改进效果进行验证,所得动态视觉搜索策略的验证结果如图1所示,k=95时荧光亮度方法的改进结果如图2所示,混沌扰动搜索策略的验证结果如表1所示.由图1可以看出:标准PF算法的有效粒子个数折损以及波动现象明显;而FA-PF算法能够显著提高有效粒子个数,但其折损波动较大,最大失效粒子数的比率约为30%;本文提出的MSFA-PF算法相较于PF算法以及未加入视觉搜索策略的FA-PF算法的有效粒子数所占比率的优势明显且波动平缓,具有极高的粒子利用效率,失效粒子得到了有效控制,从而验证了动态视觉搜索策略改进的有效性.由图2可以看出,k=95时,相较于PF算法,改进的MSFA-PF算法在迭代后期的粒子基本分散在整个状态空间,通过在荧光亮度公式中引入混沌信息,在高似然区域内丰富了粒子优化集,有效保证了粒子优化完整度,避免了粒子后期多样性较差的现象,从而验证了改进的荧光亮度方法有效性. 图1 N=100时动态视觉搜索策略验证Fig.1 Verification of dynamic visual search strategy at N=100 图2 k=95时改进荧光亮度方法的验证Fig.2 Verification of improved brightness mechanism at k=95 图3 不同粒子数时的滤波状态估计Fig.3 State estimation of filter with different particle numbers 表1 混沌扰动搜索策略的验证Tab.1 Verification of chaotic disturbance strategy 由表1可以看出,采用混沌扰动搜索策略改进后,MSFA-PF算法比原FA-PF算法的滤波精度和运行时间均有较大提高,有效权衡了算法的搜索能力,从而验证了混沌扰动搜索策略改进的有效性. 本文在N=50,100的条件下进行了几种算法的综合性能仿真测试.其中,系统的过程噪声uk~(0,1)、测量噪声nk~(0,1)均服从零均值高斯分布.本文选取PF、PSO-PF、FA-PF算法与本文提出的MSFA-PF算法进行状态估计,所得状态估计结果及其滤波误差如图3和4所示.由图3和4可以看出,本文提出的MSFA-PF算法最大程度地逼近真实状态值,未出现明显的预测偏差,具有更高的状态预测精度以及良好的预测稳定性. 图4 不同粒子数时的滤波误差绝对值Fig.4 Absolute value of filter error with different particle numbers 同时,对上述对比算法进行100次运行并取其平均值,所得算法的综合性能如表2所示.由表2可以看出,采用优化思想改进的粒子滤波算法的精度优于标准PF算法,这是由于其通过寻优来保证粒子的分布质量,但由于通过迭代来实现算法寻优,所以其在运算时间上有所牺牲.在改进的粒子滤波对比算法中,本文提出的MSFA-PF算法通过引入动态视觉搜索策略和改进的荧光亮度计算方法,使其在高斯噪声环境下仍具有极高的滤波精度,并保证了粒子预测的稳定性,即使采用较少的粒子也能够达到所需精度,其均方根误差最小,说明其预测精度最高,且随着粒子数增加,其估计精度仍优于其他算法.同时,相较于改进的粒子滤波算法中速度具有优势的IDE-PF算法,本文提出的MSFA-PF算法引入了混沌扰动策略,使得粒子能够快速收敛至最优估计, 且比 PSO-FF、FA-PF和GA-PF算法的运算时间更短. 表2不同粒子数下几种算法的综合性能对比 Tab.2Performancecomparisonofseveralalgorithmswithdifferentparticlenumbers N算 法RMSE运行时间/ms50PF5.0361112.3PSO-PF3.3762446.7GA-PF2.3765287.3FA-PF2.1873313.9IDE-PF1.2543153.1MSFA-PF0.4176140.3100PF4.1398147.4PSO-PF2.4063596.1GA-PF2.2041317.8FA-PF2.0046343.6IDE-PF1.0033176.1MSFA-PF0.2074162.1 本文提出了基于混合引导策略的萤火虫优化粒子滤波算法,结合粒子滤波特性,在萤火虫位置更新过程中加入混沌扰动搜索策略,有效权衡了粒子的探索能力与开发能力;引入动态视觉搜索策略,自适应调节粒子搜索范围,以提高粒子利用效率;改进荧光亮度计算方法,结合混沌扰动观测信息来引导粒子向优化完整域逼近,从而提高了粒子的质量.仿真实验结果表明,本文提出的改进粒子滤波算法有效提高了粒子滤波的滤波精度和滤波速度,比现有智能优化思想改进的粒子滤波算法更具有实际应用价值.2 基于混合引导策略的FA-PF算法
2.1 萤火虫混沌扰动搜索策略
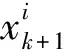
2.2 萤火虫动态视觉搜索策略
2.3 萤火虫荧光亮度计算方法的改进
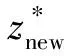
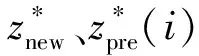
2.4 算法流程
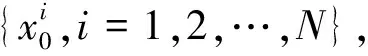
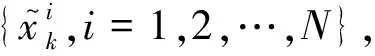
3 仿真实验
3.1 算法改进效果的验证
3.2 算法的综合性能仿真测试
4 结语

