基于增量稀疏核极限学习机的柴油机故障在线诊断
刘 敏, 张英堂, 李志宁, 范红波
(陆军工程大学石家庄校区 七系, 石家庄 050003)
柴油机故障在线诊断是在设备不停机状态下对其运行中故障进行及时发现、诊断并排除,从而维护设备安全可靠运行的有效手段.在线诊断具备对实时样本进行再学习以更新自我诊断精度的能力,从而解决了离线诊断因基于少量标记样本进行一次性学习而导致的诊断模型准确性与泛化性较差的问题.但是在线诊断中,由于样本在线贯序累积,利用新旧样本全体对诊断模型重复建模,会导致模型膨胀、过学习和更新时间过长,所以难以满足在线处理的实时性与准确性要求[1-2].
样本稀疏化和增量式建模是解决以上问题的有效方法[3-4].文献[1]中提出在线贯序极限学习机,实现了新样本扩充后模型的增量更新,但由于极限学习机泛化性能较差,且未对样本进行稀疏化,模型在线诊断效率有待提高.Huang等[5]提出的核极限学习机(KELM),相比于极限学习机和支持向量机等,具有较快学习速度和更好的稳定性与泛化性.文献[6]中提出在线贯序核极限学习机(OSKELM)分类模型,但未对样本进行前向稀疏与后向删减,且未限制模型规模,从而导致模型膨胀和在线更新效率较低.文献[7]中基于滑动时间窗与Cholesky分解提出了带有遗忘机理的在线KELM(FOKELM),虽具备旧样本后向删减能力,在一定程度上限制了模型膨胀,但由于无法区分新样本中的有效和冗余样本,导致在线模型的泛化性与时效性较差.文献[8]中提出了基于近似线性独立(ALD)的OSKELM(ALD-OSKELM),通过预设误差阈值筛选有效样本更新学习模型,实现了样本的有区别取舍,但阈值设定的人为经验误差较大,自适应性较差.
针对在线诊断中样本稀疏化效率低、模型膨胀和更新速度慢等问题,本文提出了增量稀疏核极限学习机(ISKELM)算法.首先基于瞬时信息测量筛选有效新增样本,通过字典扩充与修剪策略,在线构造具有预定规模的稀疏核函数字典;然后提出改进的减样学习算法对核函数权重矩阵进行递推更新,最终实现ISKELM分类器的在线增量建模.故障分类实验结果表明,ISKELM模型极大地提高了故障在线诊断速度且具有较高的分类精度,并能更好地满足在线诊断的时效性与准确性需求.
1 增量稀疏核极限学习机基本原理

(1)
式中:β=[β1β2…βL]T,为隐层输出权重矩阵;h(ui)=[h1(ui)h2(ui)…hL(ui)],为一个从n维输入空间到L维隐层特征空间的特征映射向量.
ELM的训练目标是训练误差和输出权重范数的最小化,可以表述为
(2)
通过解最优化方程可得
β=HT(γ-1I+HHT)-1Y
(3)
式中:H=[h(u1)Th(u2)T…h(ut)T]T,为所有输入的映射矩阵;Y=[y1y2…yt]T,为输入对应的目标输出矩阵;γ为惩罚系数.应用Mercer条件定义核矩阵G=HHT;G(i,j)=h(ui)·h(uj)T=k(ui,uj).由此可得KELM模型的输出为
(4)
式中:
(5)
(6)
分别为核函数矩阵和KELM的输出权重矩阵.
由式(4)可知,随着样本数的增加,模型的计算复杂度急剧增大,在线化处理困难.因此,本文通过筛选有效样本并删除冗余样本对k(·)进行稀疏化处理,从而提高建模效率.稀疏表征理论中定义由匹配信号中不同模式的基函数组成的变换矩阵为字典[9].参考上述定义,可利用核函数矩阵k(·)中的有效元素构造稀疏核函数字典如下:
Dt={k(c1,·),k(c2,·),…,k(cm,·)}
(7)
则ISKELM模型在t时刻的输出可定义为
(8)
式中:{c1,c2,…,cmt}⊂{u1,u2,…,ut},ci为第i个有效样本;m为当前模型的阶数;αi,t为t时刻第i个核函数的权重,且m≪t.
设t+1时刻,得到新的未标记样本为ut+1,利用已有模型对其进行预测标记得到初始预标记样本(ut+1,yt+1):
(9)
为了从大量初始预标记样本中筛选有效预标记样本,对稀疏核函数字典进行增量扩充,本文提出了基于瞬时信息测量的稀疏核函数字典在线构造方法.
2 基于瞬时信息测量在线构造稀疏核函数字典
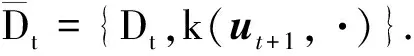
定义1假设在Tt下,训练样本ut+1的瞬时后验概率为pt(ut+1|Tt),则ut+1中包含的可以转移到当前字典Dt的信息量定义为ut+1在时刻t的瞬时条件自信息量,即
I(ut+1|Tt)=-lgpt(ut+1|Tt)
(10)
定义2假设在Tt下,字典Dt的元素个数为m,核中心ci(1≤i≤m)的瞬时后验概率为pt(ci|Tt),则将字典Dt在时刻t所具有的平均自信息量定义为Dt的瞬时条件熵,即
(11)
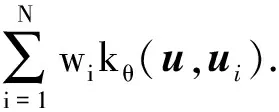
(12)
于是,对于Tt下的字典Dt={k(c1,·),k(c2,·),…,k(cm,·)},基于KDE的核中心瞬时条件PDF可表示为
(13)
因此,输入ut+1的瞬时条件自信息量和字典Dt的瞬时条件熵分别为
本文基于I(ut+1|θ,Tt)和H(Dt|θ,Tt)筛选有效样本并剔除冗余样本,在线构造稀疏化核函数字典,其基本过程包括扩充阶段和修剪阶段,如图1所示.本文采用的核函数均为单位范数核,即∀u∈U,k(u,u)=1.
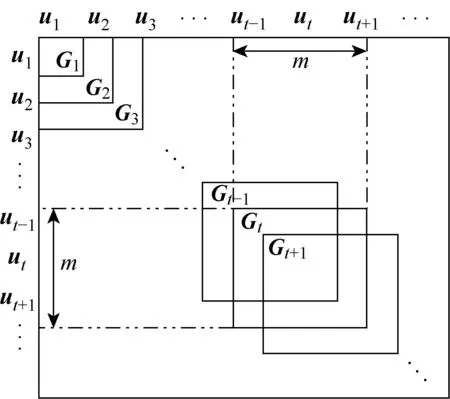
图1 核矩阵Gt的变化过程Fig.1 Kernel matrices Gt of growing size
2.1 稀疏核函数字典在线扩充策略
设et=[11…1]T∈Rm×1,字典Dt的Gram矩阵为Gt,计算矩阵St=Gtet,即
(16)
根据KDE,字典Dt中第i个核中心ci在Tt下的瞬时条件概率为pt(ci|θ,Tt)=St(i)/m.所以字典Dt的瞬时条件熵为
(17)
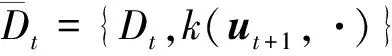
(18)
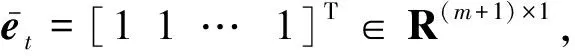
(19)
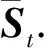
中第i个核中心的瞬时条件概率
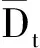
(20)
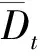
(21)
(22)
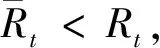
2.2 稀疏核函数字典在线修剪策略
当字典Dt的大小达到预定规模,即m=M时,在t+1时刻将执行修剪策略.从m+1个潜在元素中选择m个元素,使得所选元素具有最大的瞬时条件自信息量.
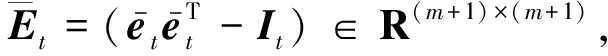
(23)
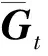
(24)
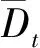
(25)
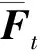
(26)
(27)
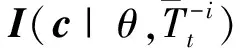
(28)
字典中每个元素具有的瞬时自信息量越大,说明彼此之间越不相似,字典所包含的信息量也越大[4].为最大化字典中每个元素的瞬时自信息量,可通过如下公式确定要删除的元素的下标:
(29)
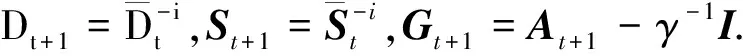
(30)
得到,Gt+1由后续算法得到.
由以上分析可知,本文提出的方法根据新旧样本对字典更新的贡献差异性对大规模样本进行稀疏化,在加入新样本前删除重要性最小的样本,提高了稀疏核函数字典在线构造效率与精度.而且字典构造计算复杂度为O(m),在稀疏化条件下,m值有限且较小,满足实际在线应用的需求.
3 ISKELM核权重矩阵递推更新
3.1 增样学习算法
当字典规模小于M时,如果新的训练样本满足2.1节中的条件,则用于扩充字典,同时对核权重矩阵α=(γ-1I+G)-1Y进行递推更新.在t时刻,记At=γ-1I+Gt.
对于训练样本(ut+1,yt+1),则有
(31)
式中:kt=[k1,t+1k2,t+1…km,t+1]T;vt=γ-1+kt+1,t+1.利用块矩阵求逆公式,可得At+1的逆矩阵为
(32)
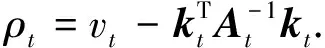
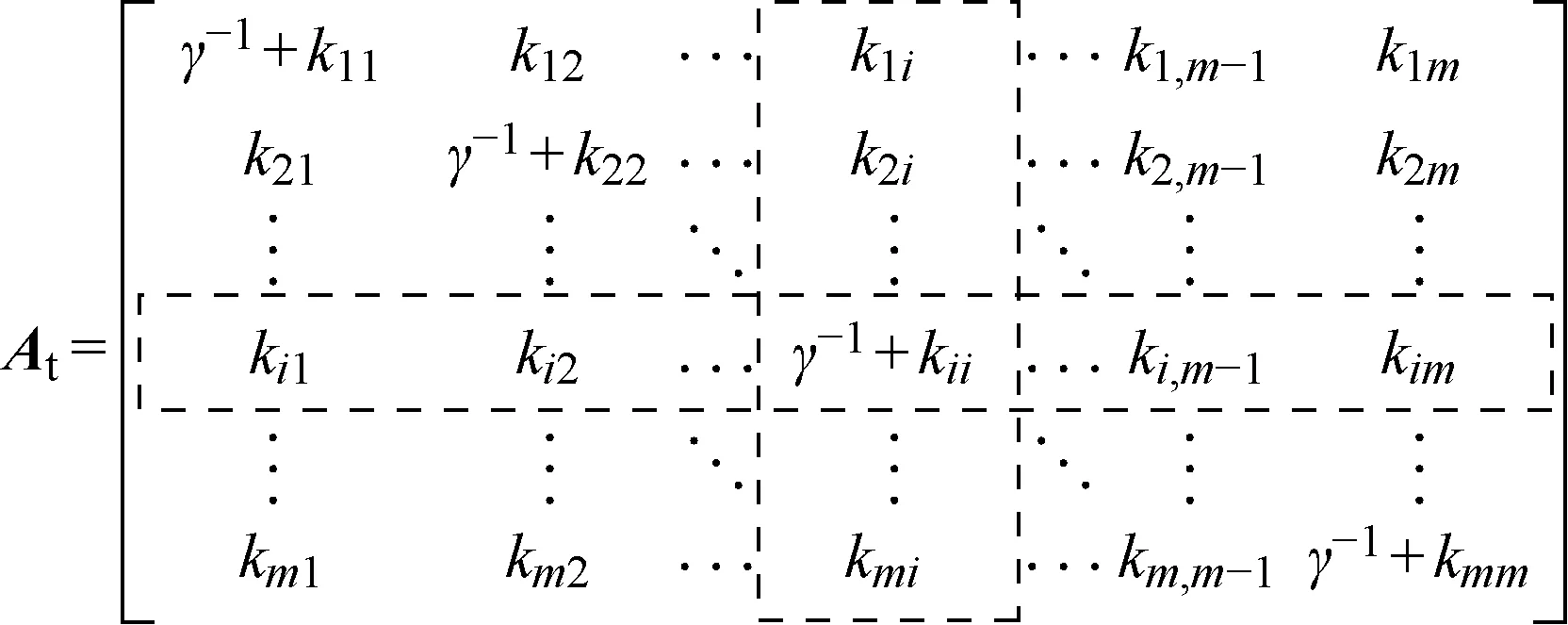
图2 矩阵变换前的AtFig.2 At before matrix transformation
3.2 改进的减样学习算法
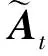
(33)

(34)
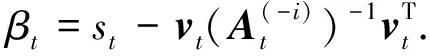
根据公式(33)和(34)可得
(35)
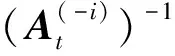
(36)
(37)
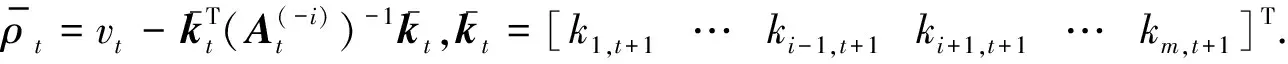
本文提出的方法基于当前模型对核权重矩阵进行增量递推更新,无需对新旧样本全体进行重复性批量学习,极大地缩短了训练时间,递推更新计算复杂度为O(m2),满足实际在线应用需求.
4 实验应用与分析
4.1 UCI标准数据分类实验
为验证本文方法的有效性,选取UCI标准数据库中的iris、liver和Diabetes数据集进行分类实验.利用ISKELM模型进行在线分类与诊断的具体过程如图3所示.
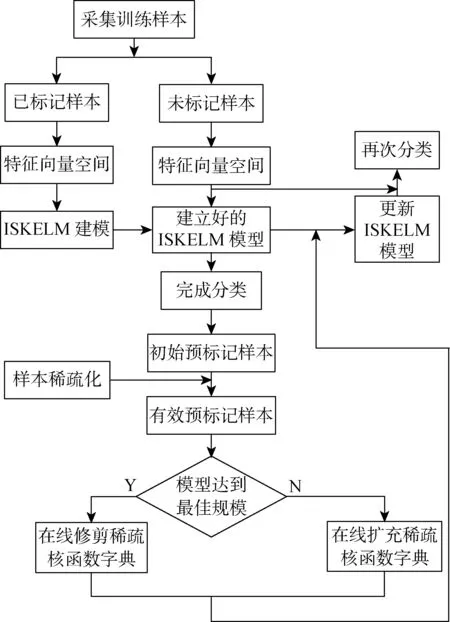
图3 ISKELM在线分类与诊断流程图Fig.3 Online classification and fault diagnosis flow chart of ISKELM

表1 各诊断模型对3个数据集的在线训练时间与测试准确率Tab.1 Online training time and test accuracy of every diagnosis model for 3 data sets
iris、liver和Diabetes数据集的特征维数分别为4、6和8,类别数分别为3、2和2.分别从3个数据集中任选500个样本作为训练样本,其中100个作为已标记样本对ISKELM进行训练,建立初始分类器,其余400个作为初始预标记样本,并将其按每组50个样本分为8组,模拟在线数据对初始分类器进行训练更新.任选200组数据作为测试样本,用于验证分类器的分类性能.
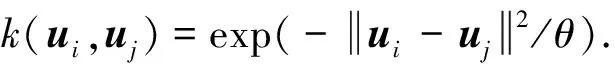
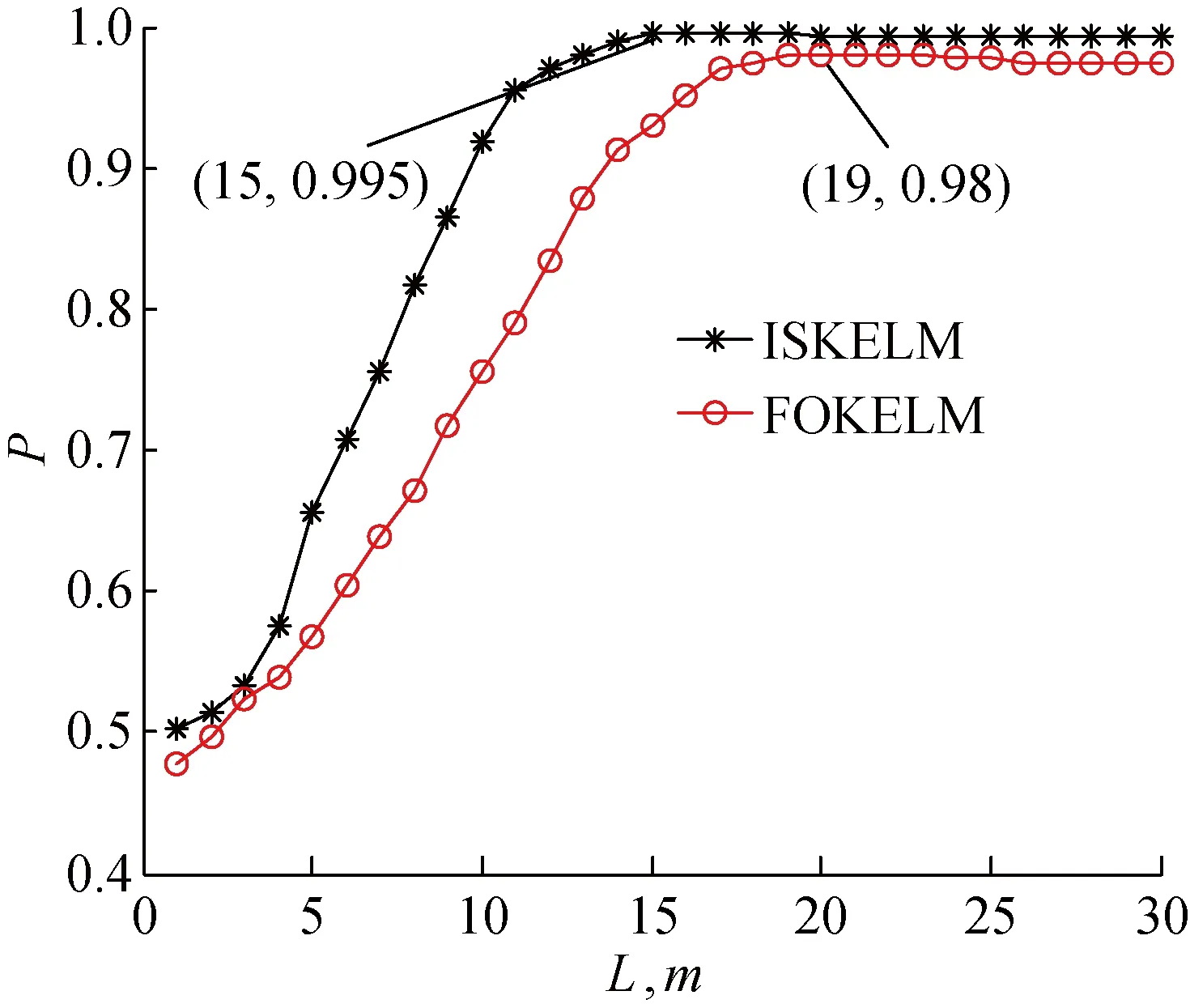
图4 训练准确率P随L与m的变化关系曲线Fig.4 Curves of training accuracy P varies with L and m
由图4可知,分别取FOKELM的时间窗长L=19,ISKELM的字典规模m=15,可使得模型分类精度最高且规模最小,同时可防止模型过度膨胀.进而通过网格搜索法获得FOKELM与ISKELM的(γ,θ)最佳值分别为(487,2.33)和(365,1.24).
根据以上4种分类器的最优参数建立初始诊断模型,进而利用3个数据集的400个初始预标记样本对各模型进行在线训练更新,并利用200个测试样本对最终模型进行分类性能测试,得到各诊断模型的在线训练时间与测试准确率如表1所示.
由表1可知,对于3个数据集,4种分类器均具有较高的分类准确率, ISKELM的分类精度高于99%,满足故障诊断要求.同等条件下,ISKELM的在线建模效率远高于另外3种分类器,对3个数据集的在线训练速度分别为FOKELM的 6.17 倍,OSKELM的 14.79 倍和SVM的 66.57 倍.这是由于SVM需要不断对全体新旧样本进行重复批量式建模而耗费了大量时间, OSKELM未对样本稀疏化且模型不断膨胀导致在线建模时间过长,而FOKELM未对新增样本进行筛选导致训练时间延长.综上分析可知,ISKELM具有较高的在线建模速度和分类精度,满足故障在线诊断需求.
图5所示为ISKELM增量更新过程中初始预标记样本数与有效预标记样本数之间的关系曲线.由图可知,在整个训练过程中对于400个新增训练样本只有240个样本参与了ISKELM模型的更新,因此训练时间极大缩减.
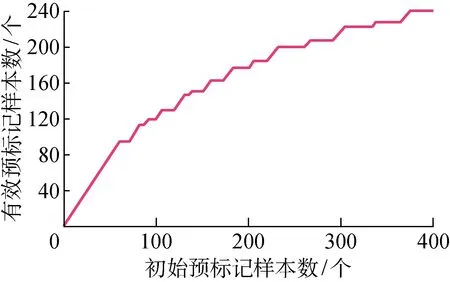
图5 ISKELM中在线样本稀疏化过程曲线Fig.5 Online sample sparseness process curve of ISKELM
4.2 柴油机故障在线诊断实验
柴油机故障在线诊断实验在F3L912型柴油机实验台架上进行.实验中,在第1缸上分别设置了8种不同工况:正常工况、进气门间隙过大、进气门间隙过小、排气门间隙过大、排气门间隙过小、进气门漏气、排气门漏气和1缸失火.采集第1缸缸盖振动信号作为诊断信号,采样频率设置为40 kHz,采样长度为1 s,每种工况下采集50组信号.实验台架如图6所示,正常工况和1缸失火2种典型工况下采集的缸盖振动信号对比如图7所示.

图6 F3L912型柴油机试验台架Fig.6 Experiment bench of F3L912 diesel engine
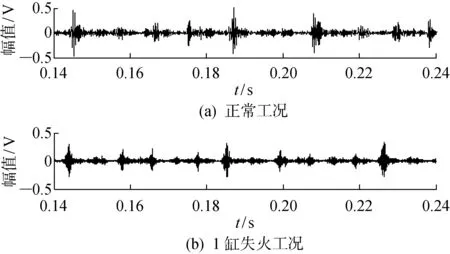
图7 缸盖振动信号时域波形Fig.7 Time domain waveform of the cylinder head vibration signal
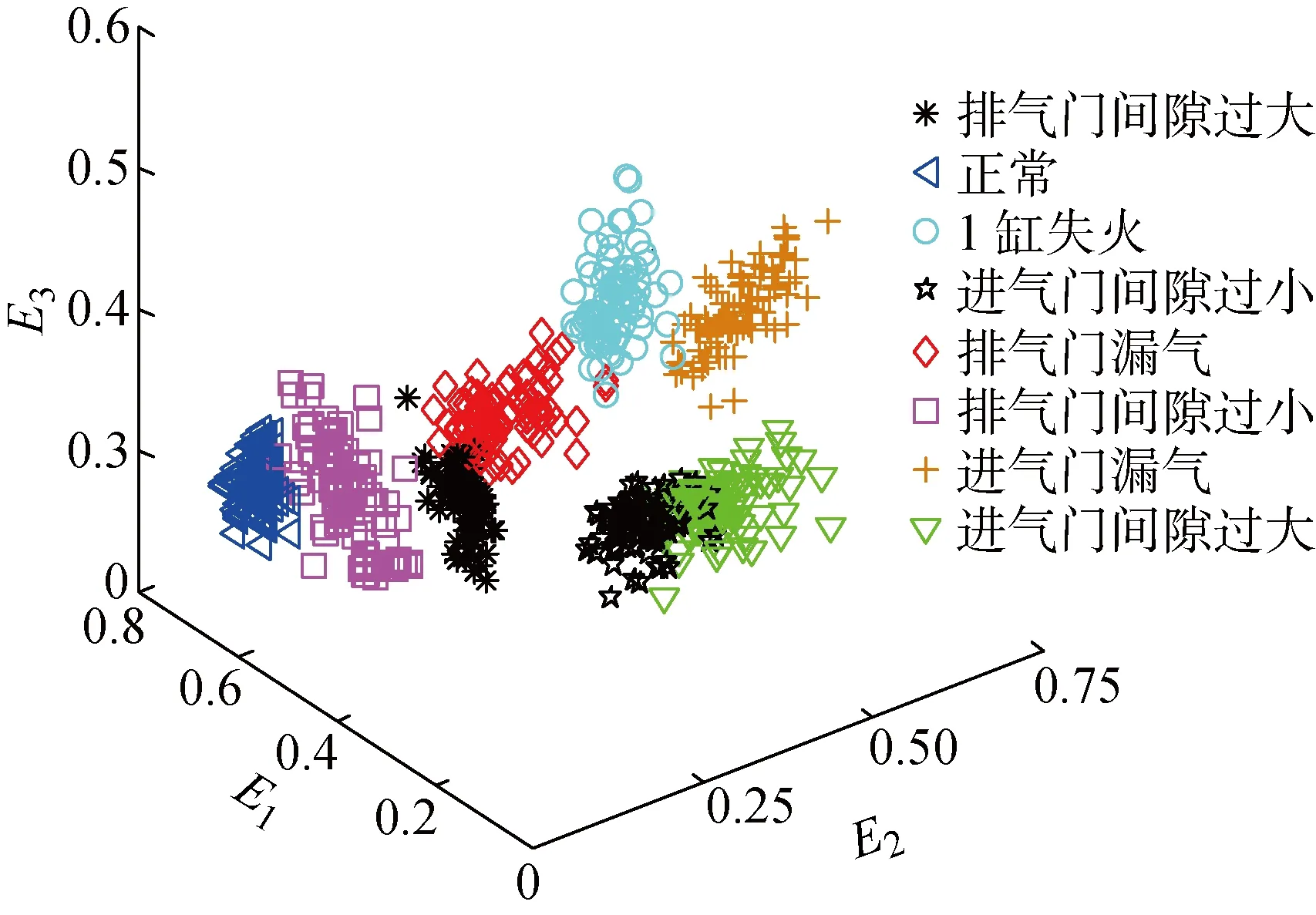
图8 缸盖振动信号能量特征三维分布图Fig.8 Three-dimensional graph of energy characteristics of cylinder head vibration signal
缸盖振动信号中不同振源的振动能量集中于不同频带,在不同故障模式下,各频带能量分布特征不同[10].对各工况下的振动信号降噪后,经过db4小波包2层分解,得到4个子频带,计算前3个分量的能量并进行归一化构造故障特征向量[E1E2E3],用于故障模式识别.图8所示为8种工况下的能量特征三维分布图.由图可见,不同工况下的故障特征具有良好的类内聚集性和类间离散性,可以用于故障分类.
8种工况下共得到400个实验样本,随机选取300个样本作为训练样本,其余100个作为测试样本.训练样本中随机选取100个作为已标记样本训练初始诊断模型,其余200个作为初始预标记样本,并将其按每组20个样本分为10组,模拟连续变化的故障数据流在线训练初始诊断模型.分别将ISKELM、SVM、OSKELM和FOKELM模型设置为对比实验.各模型的核函数统一选用高斯核函数.在模型初始化阶段,通过网格搜索法获得SVM与OSKELM的结构参数(γ,θ)的最佳值分别为(315,2.07)和(396,4.22).通过研究训练准确率P随L和m的变化关系得到FOKELM的时间窗长L=13,ISKELM的字典规模m=7,进而利用网格搜索法获得FOKELM与ISKELM的(γ,θ)最佳值分别为(635,5.11)和(583,6.52).根据各模型的最优参数建立初始诊断模型,然后利用200个初始预标记样本对各模型进行在线训练更新,并利用100个测试样本对最终模型进行分类测试,得到各诊断模型的在线训练时间与测试准确率如表2所示.
表2各诊断模型对柴油机故障样本的在线训练时间与测试准确率
Tab.2Onlinetrainingtimeandtestaccuracyof4methodsfordieselenginediagnosissamples
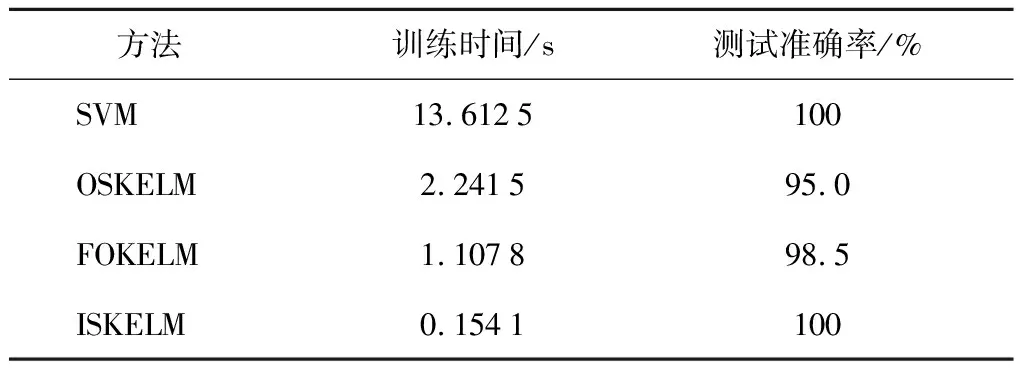
方法 训练时间/s测试准确率/%SVM13.6125100OSKELM2.241595.0FOKELM1.107898.5ISKELM0.1541100
由表2可见,与其他3种模型相比,本文提出的ISKELM利用基于前向稀疏与后向删减的样本稀疏化策略和增量递推建模方法,在保证具有较高分类精度的同时,极大地缩短了在线训练时间,提高了在线建模效率,能够更好地满足柴油机故障在线诊断的实时性与准确性要求.
5 结语
针对柴油机故障样本在线累积、诊断模型膨胀和批量建模速度慢等问题,建立了ISKELM故障在线诊断模型.该模型具有结构稀疏和规模有限的特点,根据样本对模型更新贡献大小对样本进行自适应前向稀疏与后向删减,提高了在线样本稀疏化效率,并限制了模型膨胀.ISKELM采用增样学习和改进减样学习算法对核权重矩阵进行增量递推更新,降低了算法复杂度,提高了模型在线更新速度.实验结果表明,与SVM、OSKELM和FOKELM等现有诊断模型相比,在分类精度基本相同的情况下,ISKELM具有更高的样本稀疏化效率和在线建模效率,可快速准确地实现柴油机故障在线诊断.

