多类振动噪声源下舰船水下噪声的耦合声场计算方法

李 清， 于 汉， 杨德庆

(上海交通大学 海洋工程国家重点实验室; 高新船舶与深海开发装备协同创新中心， 上海 200240)

声波是海洋中能够远距离传播的最有效能量形式，舰船水下噪声(辐射噪声与自噪声)对舰船的生存和作战性能有重大影响.舰船辐射噪声的声源级是表征舰船声隐蔽性的最重要参数，它与舰船类型、排水量、主机和辅机选型等有密切关系[1].舰船辐射噪声由机械噪声、螺旋桨噪声和水动力噪声3部分叠加而成. 机械噪声包括主机、辅机、泵系等引起的振动辐射噪声以及螺旋桨轴承力和表面力激励引起轴系振动和结构振动产生的辐射噪声.螺旋桨噪声是由螺旋桨在海水中高速转动所产生的噪声，包括螺旋桨叶片速率谱噪声、唱音和螺旋桨空化噪声.水动力噪声是由不规则和起伏的海水作用于航行舰船所产生的噪声，舰船航行时物面边界层通常由层流发展为湍流并伴有流动分离，出现明显的涡旋结构，这些非定常流动一方面直接产生辐射噪声(流噪声)，另一方面，非定常流动中的瞬态速度扰动产生脉动压力，脉动压力激励物面弹性结构振动并产生二次辐射噪声(流激振动噪声)，两者共同构成水动力噪声[2].

舰船水下声辐射是发生在船体结构和其周围流场中复杂的过程，庞大的船体结构致使水下辐射噪声求解规模大、计算难度高，建立精确解析的声振耦合模型难以实现，数值仿真技术是有效的计算手段[3]，且因产生机理各异，各类辐射噪声成分往往采用不同方法作单独研究.国内外学者对舰船在单一种类激励作用下的机械、螺旋桨以及水动力噪声均开展了深入研究，且重心主要偏向于机械振动噪声和螺旋桨噪声.针对机械噪声，邹春平等[4]计算了某船在真实机械激励下水下辐射噪声，发现比较符合实测结果；李清等[3]归纳出求解舰船水下辐射噪声的2种模式及4种数值计算方法；Zheng等[5]采用有限元/边界元方法(FEM/BEM)计算了柴油机激励导致的船体结构振动及其水下声辐射；Merz等[6]分析了螺旋桨激振力作用下潜艇的结构振动与水下辐射噪声.由于螺旋桨噪声产生方式的特殊性，往往对其单独进行讨论.杨琼方等[7]归纳了舰艇螺旋桨水下噪声的经验预测方法；Özden 等[8]采用URANS方法计算了潜艇螺旋桨不同水流条件下的水下辐射噪声；Greco等[9]基于自由尾迹法采用BEM-RANSE预报了螺旋桨的水动力及噪声性能.随着CFD技术日渐成熟，卢云涛等[10]采用RNGk-ε湍流模型计算了全附体潜艇SUBOFF三维流场并基于FW-H声类比方程对其自噪声和辐射噪声分别进行了模拟；江文成等[11]采用LES湍流模型对水滴型潜艇流场进行了模拟，并用BEM边界元法和FW-H方程分别计算了其流噪声特性；魏应三等[12]采用SSTk-ω模型计算湍流流场并基于声场精细积分算法预报潜艇流激噪声.目前有关舰艇机械噪声、螺旋桨噪声以及潜艇水动力噪声的研究已较深入，针对水面舰船水动力噪声计算的研究工作还不多.关于水面舰船在水动力、机械和螺旋桨等3类典型振动噪声源共同作用时水下辐射噪声预报方法的研究更少有论文发表.工程实践中往往是通过获取设备厂商数据、经验公式估算或数值仿真计算等方式获得各类振动噪声源谱，而后分别计算各类噪声源单独作用下舰船水下声辐射强度，最终直接叠加各噪声频谱而合成总辐射声级，忽略各类噪声源辐射声场间的耦合作用.本文旨在将上述多类舰船振动噪声源集成到统一声学环境下，探索考虑各噪声源之间耦合作用的计算方法，并探讨其计算精度和计算效率.

本文基于DTMB 5415船型，参照常见军舰上层建筑及基本结构设计了某护卫舰.采用SSTk-ω湍流模型数值模拟该舰航行时的非定常流场，并作为水动力噪声源.采用与某型螺旋桨相同的振动和噪声实测数据作为本舰的螺旋桨水动力噪声源，以等效强度的点声源模拟螺旋桨噪声源，以螺旋桨脉动压力作为机械振动源.采用基于声振耦合模式的结构有限元-声场间接边界元法(FEM-IBEM)，计算3类噪声源单独及同时作用下水面舰的水下辐射噪声，比较各噪声源辐射声级直接线性叠加方法与一体化耦合声场计算方法的差异.

1 舰船水下声辐射计算理论

1.1 水动力噪声源数值计算方法

本文采用基于RANS控制方程的SSTk-ω湍流模型计算舰体壁面边界的脉动压力，SSTk-ω模型在近壁面处采用k-ω模型，远处自由剪切流动采用k-ε模型，模型考虑了剪切力的影响，因此能够比较好地模拟强逆压梯度的流场.SSTk-ω模型中湍流动能k、湍流耗散率ω及涡黏性系数νt满足如下方程[13]：

(1)

式中：Rk和Rω分别为有效雷诺数和湍流产生项，

k-ω方程的源项sk和sω分别为

(2)

式中：β*、β、σk、σω和γ均为Blendedk-ω/k-ε模型常量；F1为混合函数，表达k-ω/k-ε模型混合使用情况；Re为雷诺数.由于舰船航行马赫数较低，水动力噪声源主要来自舰体表面的壁面偶极子声源，其强弱和分布特性决定着其外部辐射声场的强弱及其分布规律.将湍流流场信息转换为声学脉动压力[14]：

(3)

式中：p(y)为边界流体脉动压力；ny为积分面元法向量；G(x,y)为拉普拉斯方程格林函数.

1.2 结构-声耦合间接边界元

海水为重密度媒质，舰船水下辐射噪声计算必须考虑船体和流体的声振强耦合作用.声学间接边界元法可同时计算内声场和外声场，适用于舰船湿表面这类非封闭结构.满足单层势σ=0的结构-声耦合间接边界元的系统动力学方程为[3]

(4)

式中：j为虚数符号；ω为系统谐振频率；Ks、Cs和Ms分别为结构刚度、阻尼和质量矩阵；Lc为声振耦合矩阵；D(ω)为间接边界元影响矩阵；u为结构位移矢量；μ为节点双层势矢量(结构表面声压差)；Fs和Fa分别为结构与流体激励力矢量.

1.3 舰船辐射噪声声源级

舰船辐射噪声的声源级Lpo定义为在声源声轴方向上距等效声中心单位距离处的声强级[15],

(5)

式中：I为距声源声中心1 m处的声强；I0为参考声强，水声学中取I0=0.67×10-18W/m2；Wa为声源辐射声功率；DIT称为指向性指数.由于辐射声功率是表征声场能量的标量，无指向特性，本文直接选取辐射声功率为评价水下辐射噪声强弱的物理量，而声源级则可按上式进一步求得.

2 多类振动噪声源作用下舰船辐射噪声预报方法

2.1 DTMB 5415型护卫舰结构振动模型

本研究所用护卫舰简化模型在经典DTMB 5415船型基础上补充上层建筑及基本结构而成，缩尺比为 24.83，船模垂线间长 5.72 m，设计吃水 0.248 m，排水量 0.554 t，模型节点数为 13 262，单元数为 14 732，图 1所示为护卫舰结构有限元模型.本船一阶垂向弯曲振动、一阶水平弯曲振动以及一阶扭转振动固有频率分别为 1.616、2.634 和 5.042 Hz，图2所示为相应振型.

图1 护卫舰结构有限元模型Fig.1 The structural finite element model for the frigate

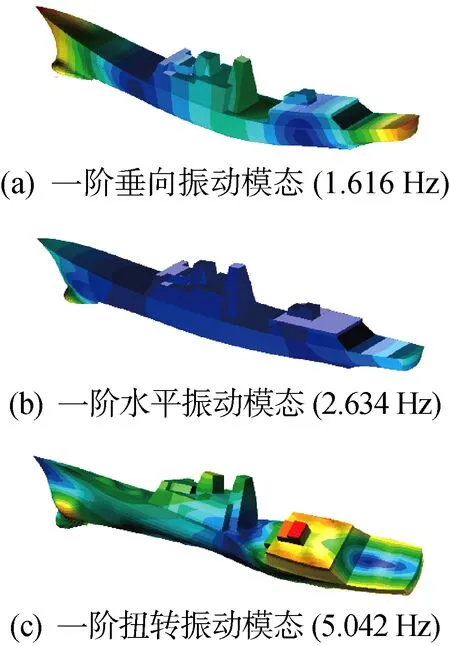
图2 护卫舰总体振动特性Fig.2 Overall vibration characteristics of the frigate

本研究声学计算的频段为0～500 Hz的低中频区间.采用模态叠加法计算船体振动响应，模态上限频率宜取2倍计算频率以保证计算精度，计算中取本船前 40 000 阶结构振动模态进行模态叠加，第 40 000 阶模态对应的固有频率已超过 1 000 Hz(1 069.698 Hz)，这时采用模态叠加法进行结构-声耦合计算可以满足精度要求.取全频段模态阻尼系数为 0.02.以上计算了船体干模态，若采用船体湿模态进行声振耦合分析，将导致重复考虑结构与流体介质间的相互影响[3].

2.2 护卫舰航行流场数值模拟

本文对护卫舰航行时的非定常流场进行数值模拟.水流引起的舰艇壳体的振动位移非常小以至于结构振动对流场量影响很小[16]，因此采用流与结构单向耦合计算湍流脉动力对舰艇壳体的流激作用.设定计算来流速度 2.06 m/s(对应实船航速20 kn)，弗劳德数Fr=0.280，雷诺数Re=1.19×107.CFD流场计算区域纵向自船艏向上游延伸 1.5 倍船长，从船艉向下游延伸3倍船长；侧面向外延伸1倍船长；垂直方向自水线面向下延伸1倍船长.计算采用非结构化四面体网格，船体表面处网格根据y+=50加密，上游为速度入口，下游为压力出口，远场设定对称边界条件，空气-水多相流采用VOF方法，计算来流为浅水波，其波速为 4.77 m/s，波幅为 0.05 m，波长为10 m，相位角为 -270°.

本例来流马赫数仅为 0.2%，按不可压缩流动求解.采用SSTk-ω湍流模型进行定常稳态RANS计算，再以定常计算结果作为初始场采用URANS方法进行非定常计算，推进若干步以获得稳定的流场.时间步长为 0.05 ms，采样频率为20 kHz，根据采样定律对应最大分析频率为10 kHz；声学信息采样 10 000 个时间步，对应物理时间为 0.5 s，频率分辨率为2 Hz.图 3所示为船体表面无量纲时均压力系数分布云图.将浸水面处时域脉动压力转移到声学网格上并进行快速傅里叶变换(见图4)，作为频域声学分析的振动噪声源.

图3 船体表面时均压力系数分布云图Fig.3 Distribution of the time mean pressure coefficient on hull surface

图4 船体湿表面流体压力脉动分布云图(10 Hz)Fig.4 Distribution of the fluid pressure fluctuation on hull underwater surface (10 Hz)

2.3 护卫舰螺旋桨噪声与振动源

在0～100 Hz低频范围内，叶片周期性切割流体产生频率为叶整数倍的线谱声，它是螺旋桨低频噪声的主要成分；当螺旋桨转速达到一定值时，叶片尖端和表面上出现空化现象产生螺旋桨空化噪声，这往往是舰船辐射噪声高频段的主要部分；螺旋桨唱音由涡流扩散激励螺旋桨叶片共振引起，是 100～1 000 Hz频率范围内的低中频强线谱[15].在舰船高航速时，螺旋桨空化噪声的连续谱将掩盖很多线谱.对给定的航速和深度频率存在某一临界值，低于此频率时，谱的主要成分是螺旋桨的线谱，高于此频率时，谱的主要成分是螺旋桨空化的连续噪声谱.目前普遍认为螺旋桨空化是最强的辐射噪声源，水面舰船在通常航态下已充分空化[7].

本舰模型采用双轴双桨推进，参考SCHOTTEL SCP 109-4XG型号螺旋桨，实桨直径 4.2 m，桨叶数4，转速为145 r/min，实桨在20 kn航速下的 1/3 倍频程(Octave)计带宽声级(BSL) (见图5)，该航速下螺旋桨已产生空泡.噪声谱级在叶频10 Hz处和二倍叶频20 Hz处出现峰值线谱，高于临界频率63 Hz噪声谱的主要成分是空化连续噪声谱，螺旋桨声级以6 dB/Oct逐渐衰减.通过如下带宽补偿关系进行换算可得实桨1/3倍频程计声压级(1/3 Oct)[16]：

SLf1=BSL(1/3 Oct)-10 lgf1+5.9

(6)

式中：f1为1/3倍频程中心频率；SLf1为f1频率处声压级.再通过下面的高速水面舰船螺旋桨空泡噪声估算公式换算到模型螺旋桨桨轴后1 mm处声压级(见图5)[17]：

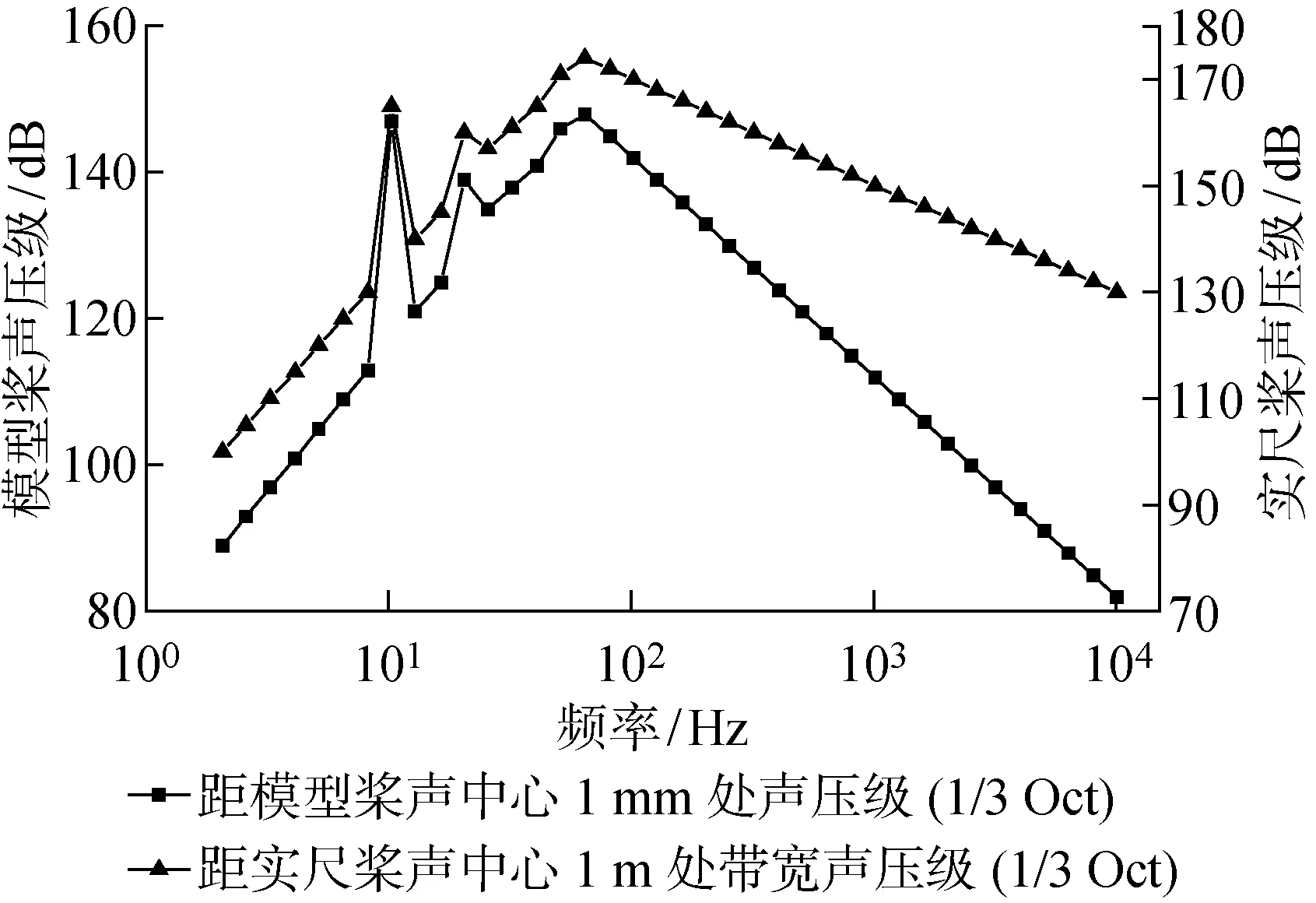
图5 SCP 109-4XG型螺旋桨声级换算Fig.5 Sound level conversion of the SCP 109-4XG propeller

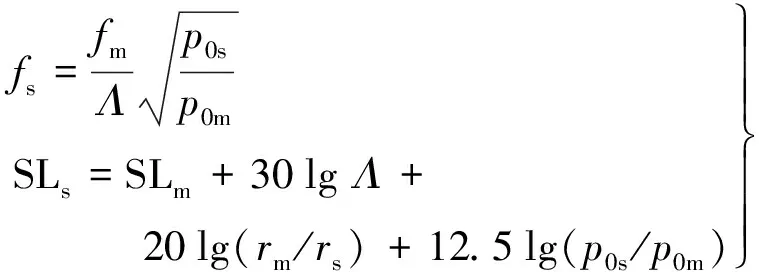
(7)

式中：Λ为缩尺比；rm为测试时点声源距测点的距离；rs为实桨距测点的距离； SLs为频率fs处的实桨噪声谱级； SLm为频率fm处的实桨噪声谱级；p0s和p0m为实船和模型螺旋桨处压力.推演模型和实桨噪声换算时遵循空泡相似、几何形状和流场相似的原则[16].本研究取p0s/p0m=Λ2以保证数值模拟的频谱特性更接近真实情况，再根据图5确定数值计算中模型螺旋桨的声源强度.螺旋桨相对于全舰振动声辐射问题其尺度可以忽略，因此将其简化成理想的单极子点声源是合适的.

航行中的舰艇在尾流中运转的螺旋桨附近形成一个随桨轴转动的不均匀脉动压力场，螺旋桨通过这种周期性的脉动水压力对流场内的船艉底板表面进行激励，称其为表面力，它是典型的周期性机械振动源之一.根据动力相似准则Fs/Fm=Λ3换算得模型螺旋桨脉动激振力(见表1)，脉动压力作用区域为(1.5D)2的方形区域，D为螺旋桨直径.

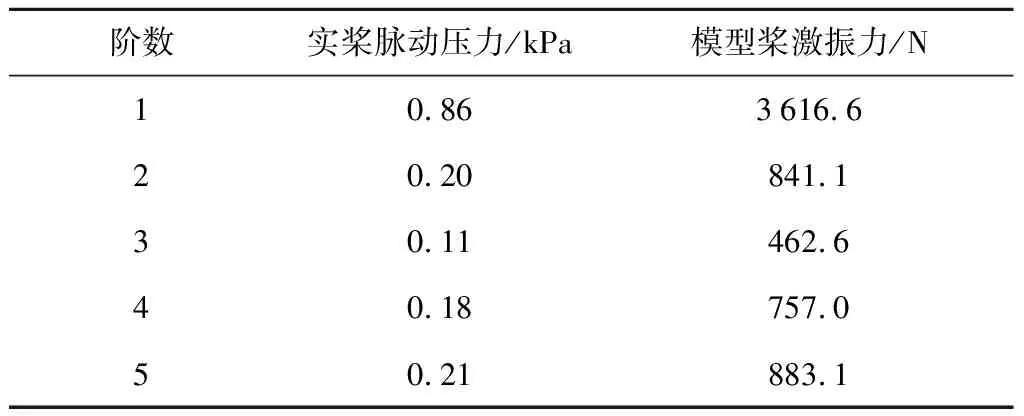
表1 SCP 109-4XG型螺旋桨激振力换算Tab.1 Excitation force conversion of the SCP 109-4XG propeller

2.4 护卫舰声振耦合数值计算模型

本研究中护卫舰0～500 Hz水下辐射噪声计算采用声振耦合分析模式[3].设定声学边界元环境，导入船体结构有限元网格与声学边界元网格.图 6所示为护卫舰声振耦合IBEM计算模型，其中声学单元特征长度为 0.05 m，计算频段最小波长内至少有6个单元.舰船外壳上的分布点是保存CFD数据信息的网格中心，通过无能量损失映射算法将壁面脉动压力转移到声学网格上，将偶极子声压等效为声压边界条件或声学载荷，作为舰船水动力噪声(流噪声或流激振动噪声)源；在船艉部螺旋桨处加载螺旋桨脉动压力(见表1)以代表性地模拟船体机械噪声振动源；在螺旋桨后1 mm处添加单极子点声源(见图 5)以模拟螺旋桨噪声源.从而实现了同时考虑水动力、机械与螺旋桨3类振动噪声源的舰船水下辐射噪声数值模拟.

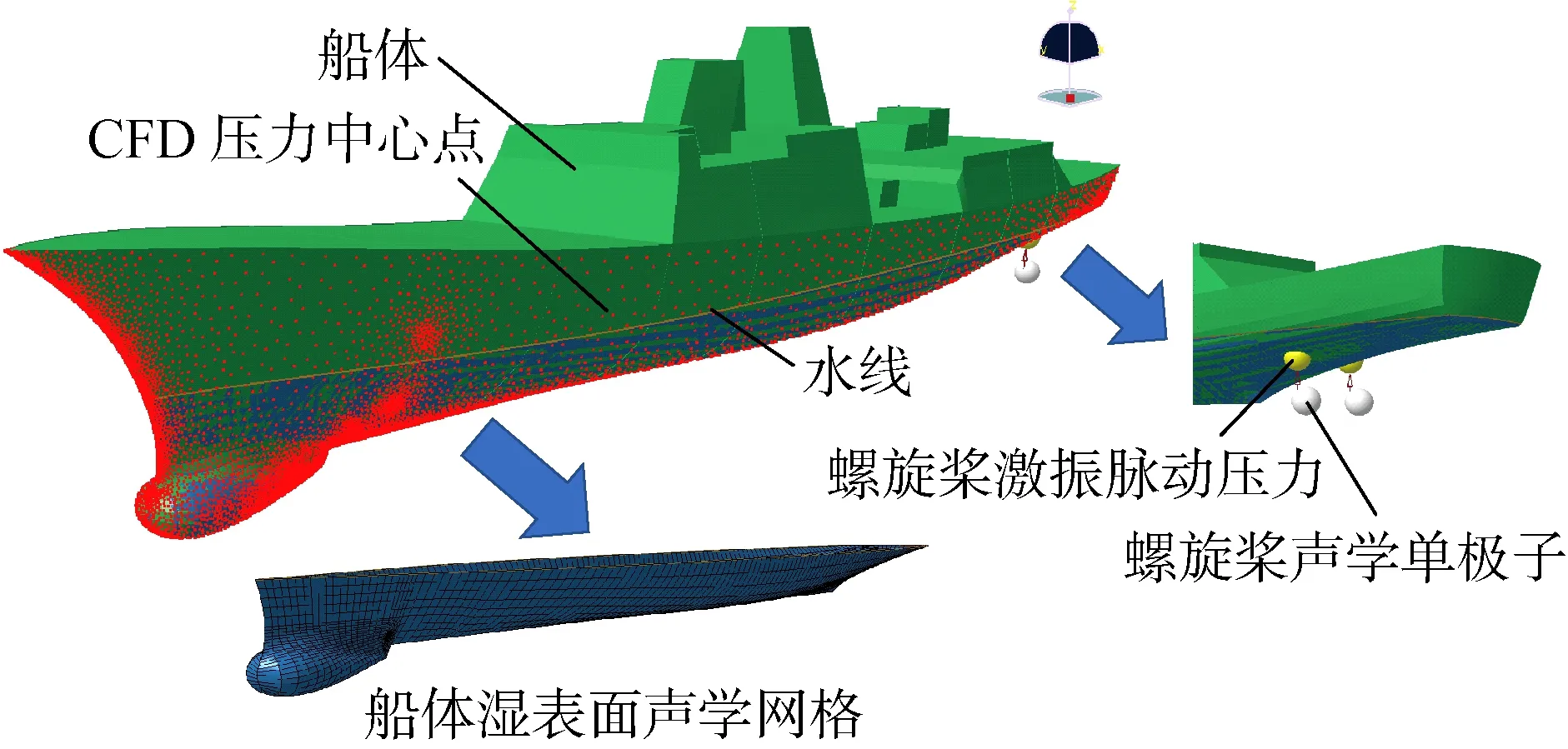
图6 护卫舰声学IBEM计算模型Fig.6 The acoustic IBEM calculating model of the frigate

求解非定常流动中的舰船辐射噪声，计算精度依赖于自由液面的流场和声学边界处理，自由液面处的声学边界应当考虑波面形状，且船体浸润区域时刻变化；本文忽略了护卫舰航行时自由面波形对水下辐射噪声的影响，边界元法近似将声学软边界取为设计水线处面内声压为零(p=0|z=0.248 m)的反对称平面(见图7)，沿用了求解机械噪声的处理方法[3].根据护卫舰模型主尺度，建立水下长 2 000 mm、深 1 000 mm场点区域观测辐射声压分布情况，并以船体模型为声源中心作标准声功率球面.取流体为海水，密度ρ=1 025 kg/m3，纵波传播速度c=1 480 m/s，导入船体振动干模态(见图2)，进行船体结构振动-声同步耦合数值计算.

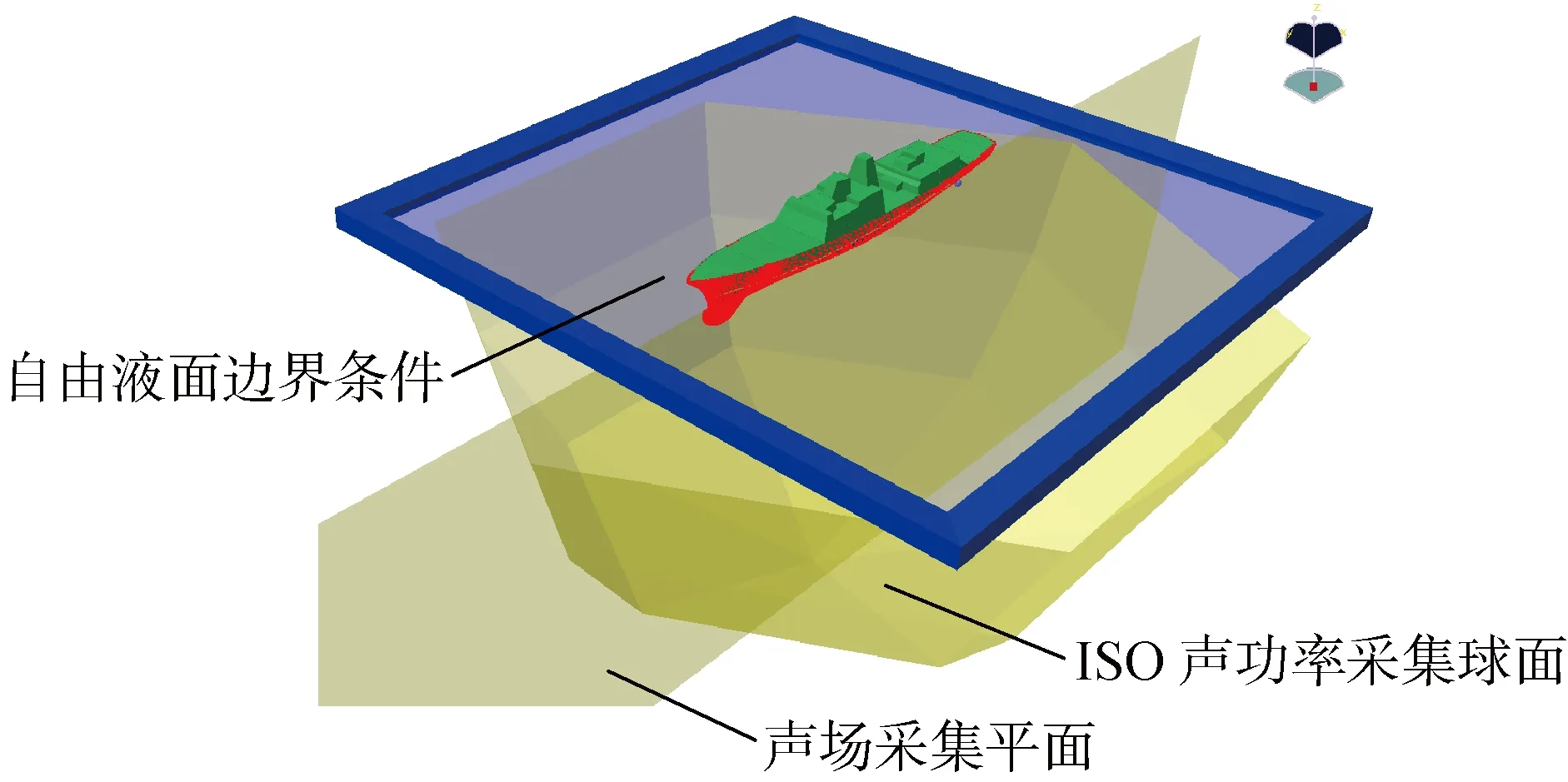
图7 声学边界条件与场点设置Fig.7 Acoustic boundary conditions and field point sets

需要指出，真正意义上的全耦合水动力、机械和螺旋桨等3类噪声源同步作用下舰船水下辐射噪声计算，应该考虑实时船舶航行状态(航速、航向、风浪流等)、船体6自由度运动(横摇、纵摇、艏摇、纵荡、垂荡、平荡)、螺旋桨转动(转速、桨叶转动与水的流固耦合作用等)、螺旋桨脉动压力、主机振动和机械设备振动等，建立包括流体力学、声学和结构动力学的全耦合联立方程组，一体化求解出船舶流场、水下辐射声场和结构力场等的相关物理量，同时涵盖流固耦合与声振耦合，这是最理想的全耦合、全实时状态的船舶力学与声学计算，目前很难实现.在声学计算前先近似获得各类声源的做法，实际上是将流固耦合与声振耦合拆分处理.本研究提出的耦合声场计算方法，实现了在声学意义上的多场多源下完全声振耦合，而各类声源的近似计算并未严格遵循流固耦合.

3 护卫舰水下辐射噪声数值计算结果分析

舰船在流体介质中运动时，船壳表面边界层发展为湍流而出现明显的涡旋结构，这些非定常流动产生壁面偶极子声源直接向周围辐射噪声(见图8).另一方面，非定常流动激励船体板壳产生二次辐射噪声(见图9).由于球鼻艏扰流作用，在其后方脱落的涡旋撞击下游船底壁面，这部分声能量聚集在船舯底板；另外，船艉几何形状变化剧烈，全船绕流流场在船艉处产生尾涡，故此处的水动力噪声亦明显，流激振动噪声与流噪声在中高频均出现多瓣指向特性，两者辐射声场的分布特征及强弱规律有所不同，但均可近似视为线声源.

由图10可知，螺旋桨脉动压力直接拍击在船艉底板表面上激起叶频(倍叶频)频率附近频段内的船体主模态，并导致全船结构振动，舰长方向的船体板壳均产生振动响应.依赖于速度连续边界条件向流体质点传递振动能量，船体由舰艏至舰艉一并向水下辐射声波，而能量大部分还是集中在舰艇艉部，艇体可视为线声源.

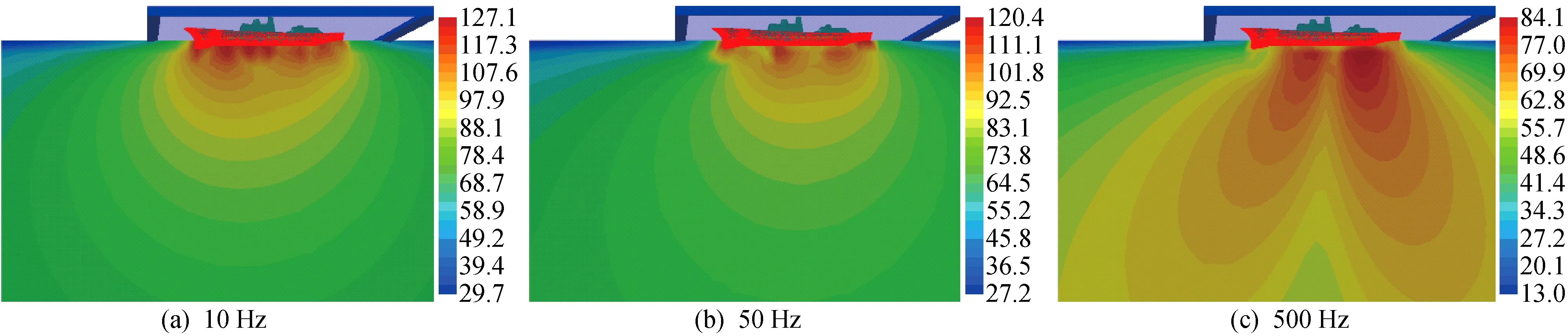
图8 流噪声声压垂向分布图(dB)Fig.8 Vertical distributions of sound pressure for flow induced noise (dB)

图9 流激振动噪声声压垂向分布图Fig.9 Vertical distributions of sound pressure for flow induced vibration and noise

图10 机械噪声声压垂向分布图Fig.10 Vertical distributions of sound pressure for mechanical noise

由图11可知，艇体螺旋桨噪声基本遵循点声源辐射规律，辐射声压与辐射半径的距离成反比，舰艇艇体作为巨大的弹性障碍物阻碍声能的传播而对声波产生散射作用，这时在空间中除点源原来的声波(初级声源)外还出现从舰体向四周散射的声波，同时，点源涨缩振动诱发周围流体质点运动，声能量传递到船体表面使弹性结构产生振动并向外辐射声波，后2种声波为次级声源.初级声源和次级声源的辐射声场叠加并相互干涉，最终将声能传递到远场.低频段艇体对声场干扰作用明显，舰长方向均有声能分布，而随着频率升高(约大于100 Hz)声波波数逐渐增大，艇体对声场的散射作用逐渐衰减，辐射声场符合单极子声源的全指向特性.

各噪声源单独激励下的声场铅垂分布在自由液面附近的声压趋于零值，符合声学软边界基本假定.图12为水动力、螺旋桨和机械噪声辐射声功率级频谱(参考声功率为1×10-12W)，符合实际舰艇中这3类噪声的辐射特征.舰艇流噪声与流激振动噪声为宽频带连续谱噪声，本研究中流激船体结构产生的辐射噪声大于船体壁面偶极子声源产生的流噪声，这取决于船体壁面几何形状、板壳厚度、舰艇航速及各频段内舰艇主模态分布等诸多因素.护卫舰耦合计算总辐射噪声声场的空间分布和指向特性与相应频段内起主要贡献的噪声源的声辐射特征一致(见图13)，总辐射噪声的远场声压宏观上随辐射半径增大遵循递减规律.

水动力噪声与螺旋桨噪声计算属于大规模流体力学计算，对于3类典型振动噪声源共同作用下舰船水下辐射噪声总的声功率计算，目前工程上常见方法是将3类噪声源单独激励下所得声功率进行线性叠加，计算结果即为舰船水下辐射噪声总声功率.图14所示为护卫舰3类噪声源单独激励并线性叠加计算方法下辐射总声功率频谱以及共同作用的耦合声场计算方法下总辐射声功率频谱，线性叠加时螺旋桨连续谱根据图12(b)的1/3倍频程谱进行线性插值.0～500 Hz计算频段内线性叠加方法下总合成辐射声功率级为 144.3 dB， 耦合声场计算方法下为 144.4 dB.声功率谱级由低频线谱和中频连续谱构成，机械噪声线谱为低频段主要噪声源，而中频段螺旋桨空化噪声连续谱占主要成分，水动力噪声有一定程度的贡献，但基本被机械和螺旋桨噪声掩盖，符合真实舰船水下辐射噪声的频谱特性.

图11 螺旋桨噪声声压垂向分布图Fig.11 Vertical distributions of sound pressure for propeller noise

图12 水动力、螺旋桨和机械噪声辐射声功率级频谱Fig.12 Spectrum of acoustic radiated power level for hydrodynamic, propeller and mechanical noise

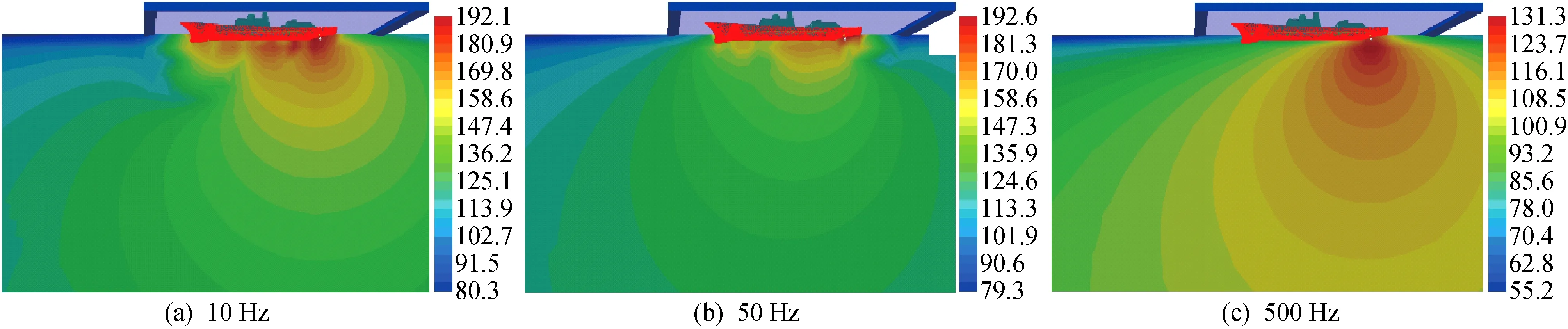
图13 耦合计算总噪声声压垂向分布图Fig.13 Vertical distributions of sound pressure for overall radiated noise

图14 水下辐射总噪声声功率级频谱(0～500 Hz)Fig.14 Spectrum of overall acoustic radiated power level (0～500 Hz)

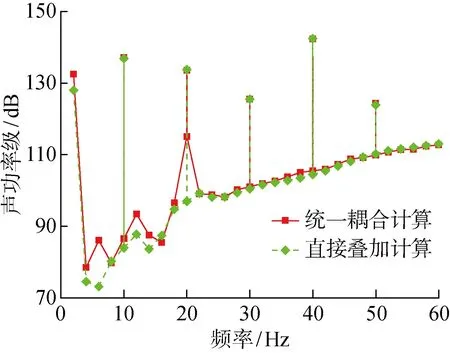
图15 水下辐射总噪声声功率级频谱(0～60 Hz)Fig.15 Spectrum of overall acoustic radiated power level (0～60 Hz)

本文对2种计算方法进行对比讨论.首先，直接线性叠加计算方法需要对3类声源激励分别进行计算和评估，相比于耦合一体化计算方法，其计算规模、计算资源需求量大且计算效率低.其次，尽管2种方法计算频段总合成声级吻合，但在计算频段内螺旋桨空化噪声为主要噪声源，计算中空泡噪声起主要作用，在低频0～60 Hz 2种方法的计算声级存在差异(见图15).最后，舰船辐射噪声的产生机理相当复杂，采用直接线性叠加计算方法会忽略3类噪声源辐射声场之间的相互干涉，且由于3类噪声源的声源中心并不在同一位置，原则上不可以直接线性相加，线性叠加方法是低中频域探讨舰船水下声辐射远场特性时忽略船体主尺度效应的近似简化方法.总体上，耦合声场计算方法计算效率和精度更高，且物理模型更合理，它考虑了由3个主要振动噪声源产生的声场间的相互耦合作用.

4 结论

本文研究了基于声振耦合模式下结构有限元-声学间接边界元计算方法，探讨了某护卫舰在水动力、机械和螺旋桨3类典型振动噪声源单独激励和共同作用下低中频水下辐射噪声特性，包括各噪声源辐射声场的频率分布特性及指向特性，采用理论线性叠加与耦合声场这2种方法计算水下总辐射声功率，得到的结论如下：

(1) 提出了多类振动噪声源共同作用下的耦合声场计算方法，相比于传统的线性叠加方法，耦合方法计算效率和计算精度更高，是多类振动噪声源下舰船低中频水下辐射噪声预报的优选算法，为国内舰船水下总辐射噪声的计算方法提供了参考.

(2) 本文计算方法仅适用于计算舰船水下辐射噪声的低中频段，高频段由于声波波长很小导致辐射声场计算无法采用有限元或边界元法，且对于低频模态分布更为密集的复杂实船板梁结构，模态叠加法的局限性决定了频段的上限频率.

(3) 固体壁面的偶极子声源的强弱和分布特性决定着其外部辐射声场的强弱及其分布规律，而URANS湍流模型无法捕捉流场涡旋的更多细节，尽管分离涡模拟(DES)或大涡模拟(LES)数值方法计算湍流流场优势比较明显，但即使是缩尺船模亦需要极其庞大的计算资源，需根据工程问题本身精度要求合理取舍，后续可基于更精细的湍流模型及声学模型作进一步探究.