基于模型预测控制的平行泊车系统研究

谢宁猛

（长安大学 汽车学院，陕西 西安 710064）

前言

随着工业飞速的发展，汽车逐渐成为人们工作与生活的重要组成部分，汽车保有量的增加以及城市建筑设施的不断扩增，不仅导致交通拥堵，汽车平均分配的停放空间也在逐渐缩小。复杂的泊车环境、有限的视野范围等多个因素最终导致泊车事故，全自动泊车系统提高了驾驶的安全性与舒适性，泊车系统分为平行泊车和垂直泊车，本文对后退式平行泊车系统进行研究。

1 自动泊车系统方案

本文的自动泊车系统的工作过程如图1所示。

图1 自动平行泊车系统工作流程

自动平行泊车系统获取车辆周围环境信息后，根据车辆与环境约束规划出可行驶区域与最优路径，得出一条光滑的参考路径，系统根据车辆当前状态生成控制命令，控制车辆准确、快速跟踪期望路径，以实现平行泊车。

2 车辆运动学模型

在良好路面的低速泊车工况下，一般不需要考虑车辆稳定性等动力学问题，车辆运动学模型满足泊车系统的控制性能。在地面固定坐标系中，车辆运动学方程形式如下：

式中：(xr,yr)为车辆后轴中心坐标，φ为车体航向角，δf为前轮转角，vr为车辆速度，l为车辆轴距。

3 平行泊车轨迹规划

自动泊车系统路径规划需满足如下约束：曲线连续、曲率无突变、各点处的位移、速度和加速度曲线光滑、计算量小，因此本文采用五次多项式拟合曲线作为汽车的倒车轨迹，以车辆后轴中心作为参考点，规定泊车起点坐标(x0,y0)，终点坐标(xd,yd)，路径表达式如下：

将车辆起始点与目标点的位置约束、航向角约束、转向平稳约束代入式（2）中，得到方程组（3），求得路径规划拟合多项式的系数。

模型预测控制器的参考路径采用含时间t的参数方程形式给出，假设车辆在参考路径匀速行驶，设参考速度v，根据曲线的长度公式以及车辆运动公式，得到一组参考状态量[xr;yr;φr]与参考控制量[vr;δf,r]关于时间t的表达式：

式中，ρ为参考点处曲线的曲率。

图2所示为车辆以v=2m/s的速度在期望轨迹上行驶的等时间间隔的曲线。

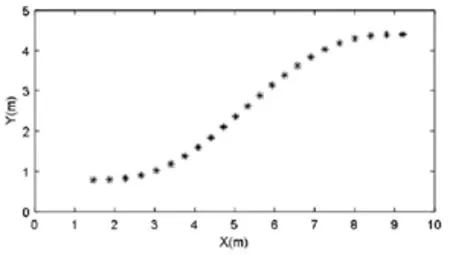
图2 车辆等时间间隔行驶参考轨迹

4 模型预测跟踪控制器

模型预测控制（MPC）考虑控制系统的非线性运动学模型并预测未来一段时间内系统的输出，通过解决带约束的最优控制问题使得系统在未来一段时间内的跟踪误差最小。而非线性系统不能直接用于线性时变模型预测控制，因此需要将运动学模型模型线性化，得到的线性时变模型为：

式中，各矩阵和状态变量为：

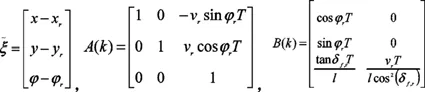
式中，T为采样时间。

控制器的目标函数要能保证车辆平稳泊车入库，采用如下形式的目标函数：

式中，Np为预测时域；Nc为控制时域；ρ为权重系数；ε为松弛因子。

在每一控制周期求解目标函数后，得到了控制时域内的控制增量，将控制序列中第一个元素作为实际的控制增量作用于泊车系统，进入下一个控制周期后，重复上述过程，实现车辆对参考轨迹的跟踪。

5 仿真实例及分析

车辆参数见表1。

表1 车辆参数表

规定平行泊车区域为14m×8m，车位尺寸为6.5m×2.5m，泊车初始点坐标x0(9.2,4.4)，目标点坐标xd(1.412,0.7893)，根据环境约束求得拟合多项式系数，得到图3规划曲线。

图3 泊车路径规划曲线

本文平行泊车控制策略在Simulink中完成，通过运行仿真平台，得出图4车辆运行轨迹。由图可知，车辆从起始点出发沿该路径进入目标车位，且与周围物体不发生碰撞。泊车起始点处切线斜率为0，即与车位平行，终点处切线斜率为0，即车辆平行车位停放。

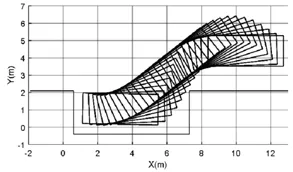
图4 平行泊车运行轨迹

6 结语

本文综合考虑泊车工况时车辆受到的约束，采用五次多项式进行轨迹规划，并运用模型预测控制器跟踪路径，通过Simulink仿真验证了设计的平行泊车系统能够使车辆稳定行驶，实现平行泊车。