压力容器中锥壳-圆柱壳连接结构的分析设计方法(一)
, ,,
(1.清华大学 工程力学系,北京 100084;2.中国石化工程建设公司,北京 100101)
0 引言
带锥壳的压力容器广泛应用于石化、航天等领域,它可作为锥形封头与一个圆柱壳相连接,也可作为连接两个直径不同的圆柱壳之间的变径段。锥壳与圆柱壳的连接处由于薄壳的边缘效应产生较高的局部应力,该局部应力随着锥半顶角的增大而升高。
在我国国家标准GB 150—2011《压力容器》[1]和行业标准JB 4732—1995《钢制压力容器——分析设计标准》(2005年确认)[2]中,基于薄壳理论的简单边界效应解[2-3],给出了与圆柱壳相连接的锥壳小端的补强设计方法,而与圆柱壳相连接的锥壳大端的设计方法则沿用了20世纪美国ASME规范中的方法,仅限于锥壳半顶角α≤30°,其结果与简单边界效应解的结果一致。
简单边界效应解在求旋转壳的边缘效应时,将一个中面半径为r=ρ2(ρ2为旋转壳在该边缘处的第二曲率半径)的当量圆柱壳的解作为其近似解。简单边界效应解只适用于所研究的边界附近,不适用于锥壳两端的边缘效应互相耦合情况。此外,当锥壳半顶角α>45°时,简单边界效应解会产生较大的误差。因此,现行标准GB 150—2011和JB 4732—1995所给出的补强设计方法存在以下问题。
(1)没有给出锥半顶角α>30°时锥形封头(锥壳大端与圆柱壳连接)的设计方法。对于大、小端分别与圆柱壳相连接的锥壳变径段,设计方法的适用范围不一致。
(2)当大、小端圆柱壳直径相差较小从而锥壳变径段较短时,JB 4732—1995附录A虽然给出了薄壳理论解,但由于受制定该规范时的条件所限,没有给出便于工程师应用的补强设计方法。
(3)现行标准规定对于α>45°的锥壳小端加强段或α>30°的锥壳大端加强段,必须设置圆环壳折边过渡段,为此将增加制造的成本。不设置折边过渡段是否可行,尚待验证。
本文根据适用于锥壳的薄壳理论解和弹塑性有限元分析,对该设计规范提出改进建议。文中仅分析图1所示内压作用下大、小端分别与两个内直径为DiL,Dis的圆筒连接的正锥壳。连接处为双面对接全焊透焊接接头,其焊缝内外表面经修磨成的过渡圆角半径r0不小于壳体的厚度δr,即r0≥δr,不带折边过渡段。采用本文所建议的该种连接方式,可以有效地降低锥壳与圆柱壳连接处的峰值应力。
以往分析[1-2]说明:在锥壳大端与圆柱壳连接处,决定加强段设计厚度的是其内壁的最大一次加二次应力强度(以经向薄膜加弯曲应力分量为主要成分),其值随锥顶角增大而加大;而在锥壳小端与圆柱壳连接处,影响设计厚度的是其总体加局部薄膜应力强度(以环向薄膜应力分量为主要成分)。前者以结构安定性准则控制,后者以极限压力准则控制。本文第一部分着重于弹性应力分析,第二部分将阐述基于塑性分析的设计准则问题。

图1 工程结构示意
1 力学模型
为解决GB 150—2011和JB 4732—1995设计方法中所采用精度较低、适用范围较小的简单边界效应问题,对于锥壳采用基于图2所示力学模型的薄壳理论精确解(薄壳理论和本文精确解的精度量级都为O(t/R),不需限制cotα值;简单边界效应解略去了薄壳理论方程中某些较小的量,其精度量级为O[(t/R)1/2],且要求cotα~O(1))代替简单边界效应解,提高了半顶角α>45°时锥壳解的精度。
对于实际工程结构(见图1),如锥壳与大、小端圆柱壳的加强段足够长,加强段外端对于锥壳与圆柱壳连接处边缘效应的影响可以忽略。假设分析所采用的力学模型中锥壳与大、小端圆柱壳为同一厚度t,文中令t=δr,并令小端圆柱壳中面半径R1=0.5(Dis+δr),大端圆柱壳中面半径R2=0.5(DiL+δr),内压为p。
以假想的旋转壳法向截面分别将小端圆柱壳与锥壳在连接处r=R1、大端圆柱壳与锥壳在连接处r=R2截开,在截面处分别作用有未知的沿平行圆径向的横剪力Q1和Q2,弯矩M1和M2,如图2所示;图2中锥壳与圆柱壳连接处内力素之间的关系满足内力的连续条件。采用“力法”求解该问题,即以Q1,M1和Q2,M2为4个基本未知量,分别给出圆柱壳和锥壳在连接处的位移、转角与基本未知量的8个关系式,再利用以4个基本未知量表示的两个连接处的位移、转角共4个变形协调条件,就可解得Q1,M1和Q2,M2,从而可得出两端边缘效应耦合的锥壳理论解。
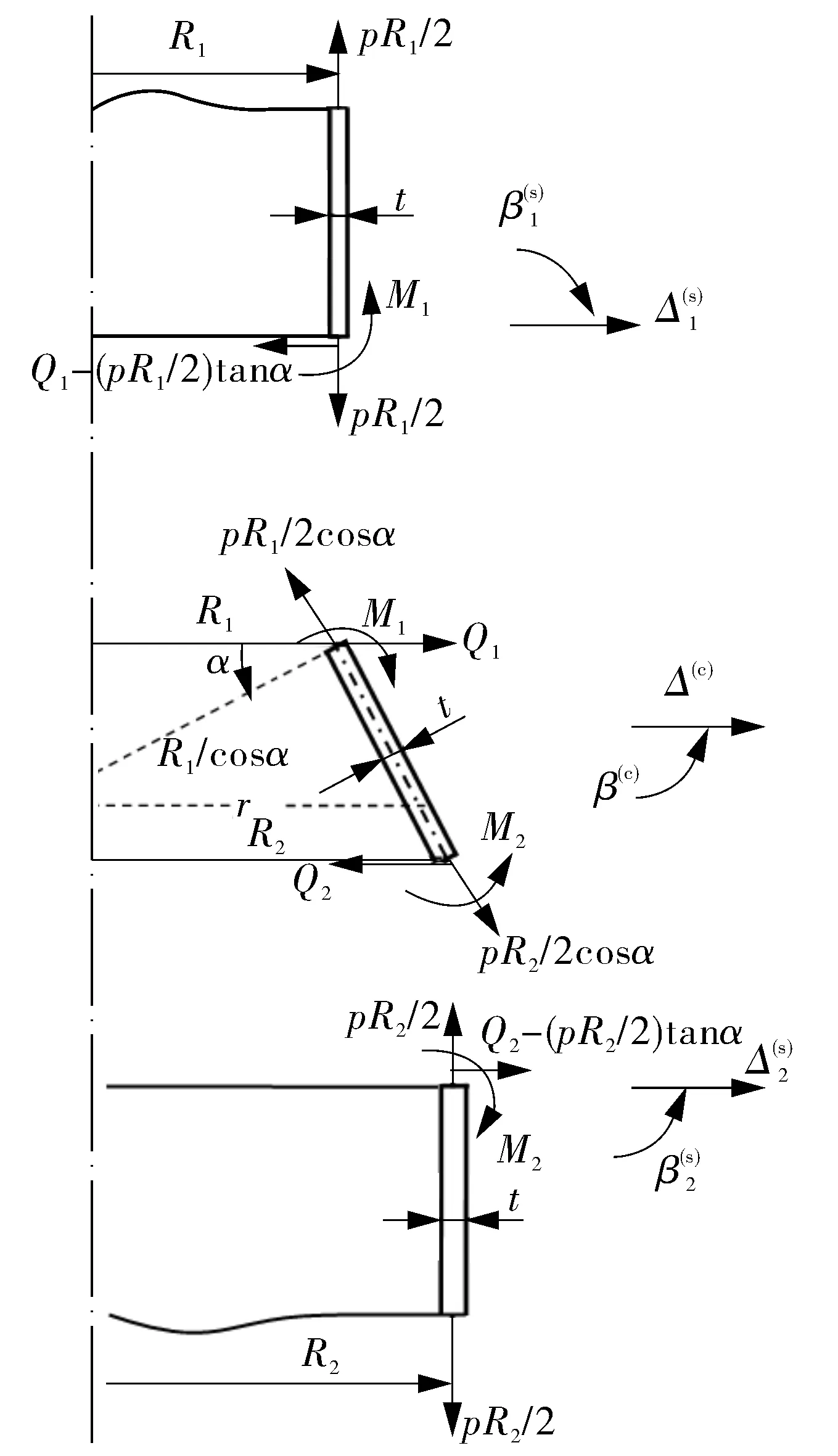
图2 力学模型
2 薄壳理论解
旋转壳的薄壳理论方程的解,可分解为薄膜理论解和对应于齐次微分方程的边缘效应解的通解,通解中的待定常数由边界条件确定,反映了壳体边缘效应的影响。本节公式可参考JB 4732—1995附录A。
2.1 圆柱壳的薄壳理论解


+ksiMi]}
(i=1,2) (1)
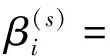
(i=1,2) (2)
式中E——材料的弹性模量;
υ——泊松比;
δi——区别大小端边缘横剪力的正负号而引入的系数;
i——下标,i=1表示小端圆柱壳,i=2表示大端圆柱壳。
圆柱壳的壳体常数:
(i=1,2) (3)
(4)


(5)
其中,克雷洛夫函数θ(x),ψ(x),ζ(x),φ(x)的表达式为:
θ(x)=e-xcosx,φ(x)=e-x(cosx+sinx)ζ(x)=e-xsinx,ψ(x)=e-x(cosx-sinx)
(6)
(i=1,2) (7)
只需将上述式(5)和式(7)中的Ri改为Ri/cosα,边缘作用剪力(Qi/pRi-tanα/2)改为-Qicosα/pRi,仍令i=1,2,可分别得到锥壳小端与大端的简单边界效应解,即文献[1-2]中设计方法的理论依据。
2.2 锥壳的薄壳理论解

(8)
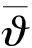
(9)
其中,D为锥壳的弯曲刚度,其表达式与圆柱壳相同:
D=Et3/12(1-υ2)
(10)
锥壳混合型的基本方程为:

(11)
其中L为对坐标s的二阶常微分算子:
(12)
方程组(11)可化为一个二阶复函数的方程,经过变量代换后,化为虚宗量的贝塞尔方程,其详细推导过程见文献[4],本文仅给出结果。将自变量s由下式的关系代换为x:
(13)
其中,壳体常数μ4=Et/D=12(1-υ2)/t2。得到:

(14)
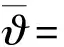
(15)

将式(14)代入式(8)中的Qr表达式,将式(15)代入式(9)中的Ms表达式,并取锥壳小端与大端的x值,可以得到:
(16)
其中,系数矩阵aij(i,j=1,2,3,4)分别是开尔文函数和汤姆逊函数及其一阶导数在小端和大端的表达式,详见文献[2]附录A中式(A2-20)。锥壳在小端与大端的壳体常数kc1,kc2为:
(17)

(18)

(19)
其中,系数矩阵bij(i,j=1,2,3,4)分别是开尔文函数和汤姆逊函数及其一阶导数在小端和大端的表达式,详见文献[2]附录A中式(A2-21)。将式(16)的系数矩阵求逆,代入式(19),可得到锥壳两端边缘位移、转角与内力素的关系:
(20)
2.3 锥壳与圆柱壳的变形协调
锥壳与圆柱壳的变形协调方程如下:
(21)
将式(1),(2)代入式(21)左端,式(20)代入式(21)右端,就可解得基本未知量Q1,M1和Q2,M2的表达式,它取决于内压p及圆柱壳、锥壳的基本几何参数t/R1,R2/R1,α以及材料常数E,υ等已知条件。
2.4 锥壳与圆柱壳中的薄膜应力与弯曲应力


(22)

(23)
弯曲应力分量(即二次应力)如下:
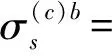
(24)

(25)
弯曲应力表达式中,“-”为外壁应力,“+”为内壁应力。
将所求得的Qi,Mi代入式(5),(7),并令i=1,2,可分别得到小端与大端圆柱壳中的薄膜应力和弯曲应力。
3 连接结构形式的确定与理论解验证
为确定合理的连接结构形式、验证理论解的可靠性,并与简单边界效应解对比,采用轴对称弹性有限元法对一系列不同α,t/R1和R2/R1的结构进行了计算,有限元模型采用8节点轴对称二次单元进行分析。图3示出一个典型的有限元网格在锥壳与圆柱壳连接部位的局部放大图。下文所给各算例中,R1=1 000 mm,R2=1 100 mm,t=10 mm,内压p=0.4 MPa。

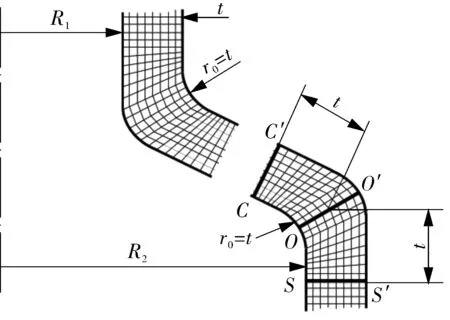
图3 有限元分析网格局部图

r0/t00.20.40.60.81.0理论解(σs)max/MPa1 187981808695624573(σms+σbs)max/MPa533421412407403399536
从表1可以看出:
(1)过渡圆弧半径r0可显著降低该处的峰值应力,当r0等于壳厚t时,该截面的最大应力已经降低至无过渡圆弧时最大应力的48%,此时峰值应力仅比薄壳理论解的计算值高7%;

图4示出当r0=t时,沿图3中连接处壳体3个法向横截面O-O′,C-C′和S-S′上经向应力有限元计算值和理论解的分布规律(设各横截面的厚度为δ)。O-O′对应的理论解为锥壳与圆柱壳中面的交点处之值,C-C′和S-S′对应的理论解分别为锥壳和圆柱壳各自距离中面交点10 mm(即壳厚)处之值。从图4可以看出,在距离中面交点一倍壁厚处,理论解与有限元解吻合很好,而过渡圆弧处的应力峰值仅经过一倍壳厚的距离便已迅速衰减。
图5,6示出算例α=40°,R2/R1=1.1的精确解、简单边界效应解和有限元解沿壳体经向的分布规律。该算例中所显示的简单边界效应解(不计锥壳大小端边缘效应耦合)与精确解的误差为:大端内壁经向应力是整个结构的最大应力,其误差-13.2%,该一次加二次应力误差对于大端工程设计厚度的影响偏薄,但就实际工程设计而言,尚属可接受的偏差范围;算例中最大环向薄膜应力发生在小端,简单边界效应解的误差达13.4%,此误差说明不考虑耦合效应使小端设计厚度偏于保守。计算发现:

图4 r0/t=1时锥壳与圆柱壳连接区经向应力沿壁厚的分布(α=60°,R2/R1=1.3,t/R1=100)
(1)对于所有算例,考虑锥壳两端边缘效应互相耦合的精确解与有限元解都能很好地符合;
(2)精确解与简单边界效应解的误差随α的增加而增加,随R2/R1的减小而增加,简单边界效应解可以适用于较小的α角以及较大的R2/R1值对应的结构;
(3)对于最大一次加二次应力强度,精确解与简单边界效应解的误差不大;但是对于最大薄膜应力强度,随着α的增加和R2/R1的减小,二者的误差快速增加;
(4)需要注意锥壳两端的边缘效应耦合作用使最大薄膜应力强度不是增加、而是减少。

图5α=40°,R2/R1=1.1时经向薄膜加弯曲应力分量

图6 α=40°,R2/R1=1.1时环向薄膜应力分量
图7,8示出算例α=60°,R2/R1=1.1的精确解、简单边界效应解和有限元解沿壳体经向的分布规律。关于该算例中简单边界效应解的误差:在经向薄膜加弯曲应力取最大值的大端内壁,误差仅为-4.3%,但是环向薄膜应力取最大值的小端,误差高达52.6%。可见,当R2/R1较小时必须考虑锥壳两端边缘效应的耦合作用,考虑此作用相比原有规范[1-2]算法可减薄设计厚度。
基于对此一系列算例的分析,建议在制定设计方法时考虑如下内容。
(1)对于锥壳较长,无需考虑锥壳两端边缘效应耦合作用采用的情况(与α,R2/R1和t/R1的具体值有关),可采用本文提出的薄壳理论精确解结果,分别给出锥壳与大端圆柱壳的补强系数QL曲线、锥壳与小端圆柱壳的补强系数Qs曲线。
(2)对于锥壳较短,必须考虑锥壳两端边缘效应耦合作用采用的情况,可采用本文提出的薄壳理论精确解结果,给出与参数α,R2/R1和t/R1有关的设计厚度补强系数Qs曲线。
(3)有限元分析还说明,采用本文提出的锥壳与圆柱壳连接结构,即在全焊透焊缝内外表面经修磨成半径为r0≥δr的过渡圆角,当锥壳半顶角α超过30°时,不带折边过渡段也可以有效地降低连接处的局部应力。

图7α=60°,R2/R1=1.1时经向薄膜加弯曲应力分量

图8 α=60°,R2/R1=1.1时环向薄膜应力分量
4 设计准则
现行标准GB 150—2011[1]和JB 4732—1995[2]中,所采用的设计准则式为:
Pm⟹SⅠ≤Sm
(26)
PL⟹SⅡ≤1.1Sm
(27)
PL+Q⟹SⅣ≤3.0Sm
(28)

ps≥1.5p
(29)
准则式(29)中,ps为结构的塑性极限承载能力,p为结构的设计压力。关于此设计准则的详情将在后续第(二)部分加以论述。
5 设计方法
按照本文所给出的薄壳理论精确解以及设计准则式(26),(28)和(29),可以给出锥壳大、小端与圆柱壳相连接时的补强设计方法。文中给出锥形封头或锥壳变径段无需考虑锥壳两端边缘效应耦合时锥壳大端与圆柱壳连接的补强设计方法,以及必须考虑锥壳变径段两端边缘效应耦合结构的补强设计方法,锥壳小端与圆柱壳连接的补强设计方法将在后续第(二)部分给出。
5.1 锥壳大端与圆柱壳连接时的设计方法
当只需考虑锥壳大端与圆柱壳相连时,Di=DiL=2R2-t,此时控制加强段设计厚度(即补强系数QL值)的是准则式(26),(28),且先由图9判断是否需要补强。
连接处若需补强,加强段厚度δr=t仍按下式计算:
(30)
按本文的应力分析结果,给出QL(α,p/Sm)曲线如图10所示。
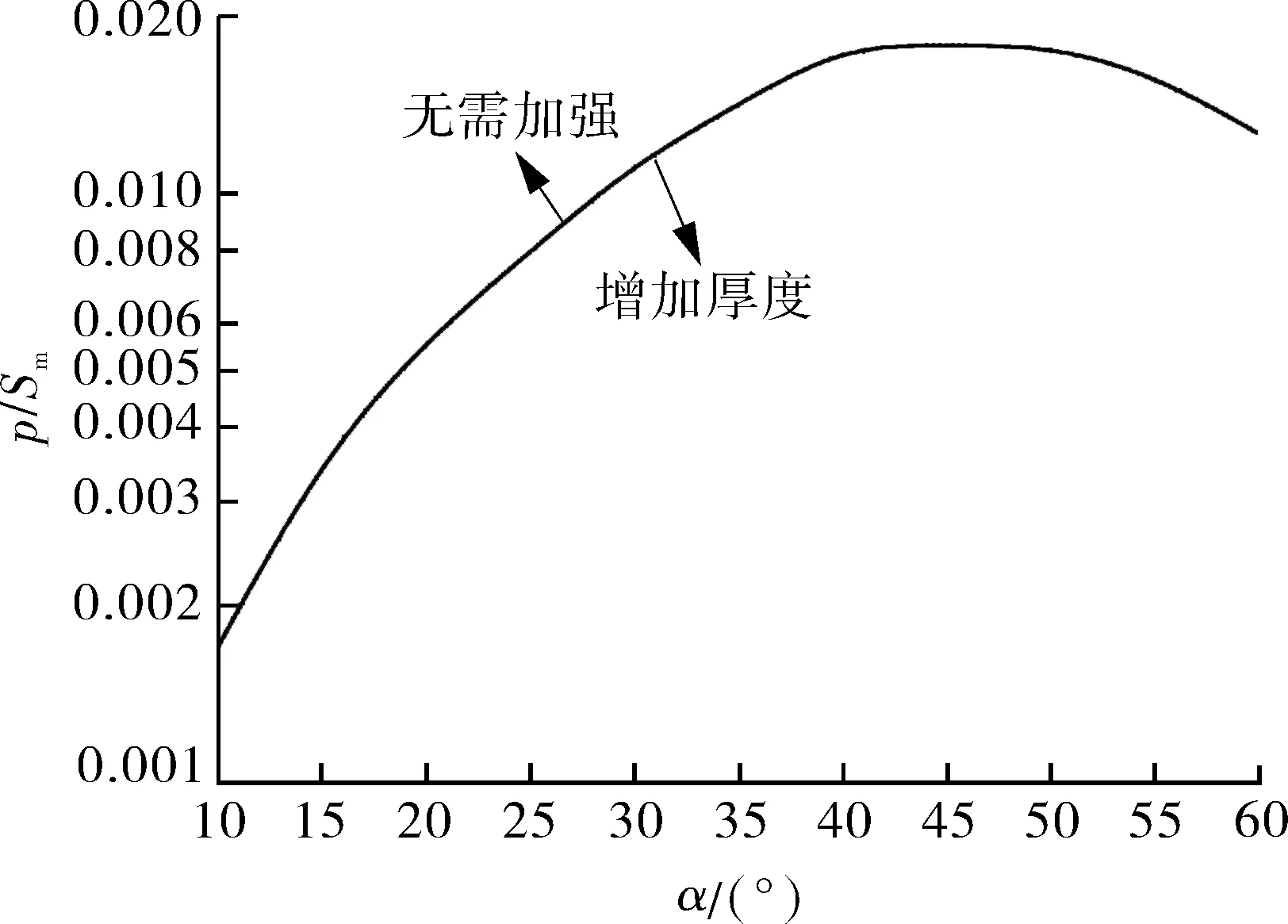
注:曲线按最大一次加二次应力强度绘制,控制值为3Sm
为验证本文所给适用范围内锥壳与圆柱壳极薄时(如p/Sm=0.001),连接处是否有内压失稳的可能,本文用理想弹塑性小变形有限元法分析了结构的极限压力,又用理想弹塑性大变形有限元法分析了该结构[8-10]。图11示出其中一个对于稳定性而言安全裕度最低的算例,其参数为:α=60°,R2/R1=1.8,R2=1 800 mm,p/Sm=0.001。算例厚度按式(30)、图10计算,最小厚度δr=9.083 mm,即按照锥壳大端-圆柱壳结构塑性极限承载能力的要求,R2/δr=198,锥壳和大、小端圆柱壳均采用此厚度。先用理想弹塑性小变形有限元法得到压力-变形历史曲线,求得塑性极限压力ps=0.353 MPa,ps/p=1.54。再采用Schmidt等[11]提出的等效几何缺陷建模法,将其一阶弹性屈曲模态作为初始缺陷,通过三维理想弹塑性大变形非线性屈曲有限元法得到结构的压力-变形历史曲线,其中结构产生1%塑性变形时,结构载荷p1=0.649 MPa,可见结构此时仍未发生失稳现象,且仍有较大的承载能力,故结构破坏模式为过大的塑性变形。

(a)内压-锥壳大端与圆柱壳连接点径向收缩变形历史曲线 (b)变形前后壳体状态放大图
图11 弹塑性有限元分析算例
对具有其他锥壳半顶角的算例,按照与上述算例相同方法进行有限元分析,结果见表2。所有算例均保证其塑性极限压力有至少1.5倍的安全裕量,满足设计准则式(29)。同时,结构产生1%塑性变形时,结构载荷远大于1.5倍设计压力p,此时结构并未发生内压失稳。
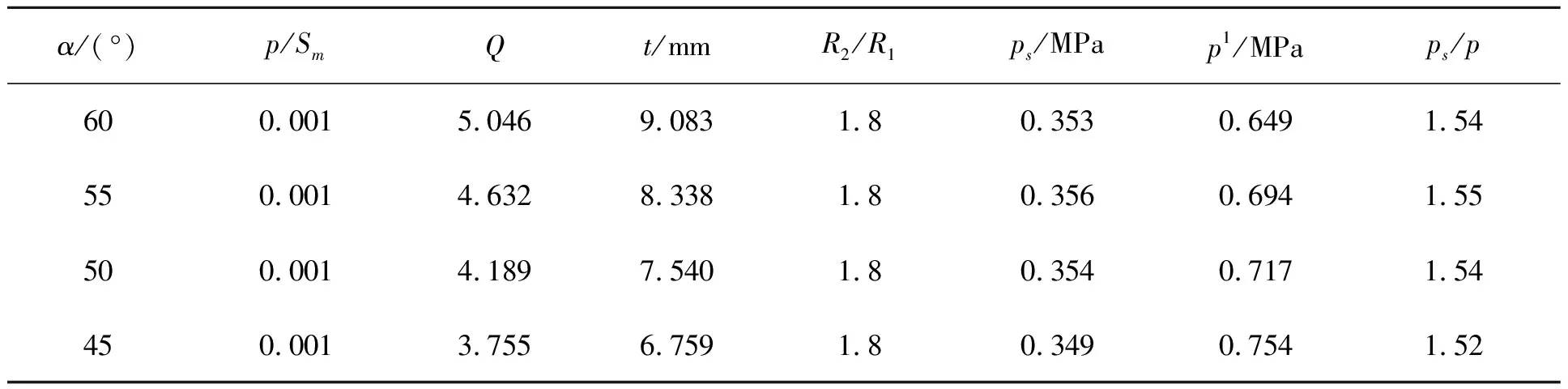
表2 与圆柱壳连接的锥壳大端结构承载能力的理想塑性有限元分析结果(p/Sm=0.001)
5.2 锥壳变径段较短时,大、小端与圆柱壳连接处边缘效应耦合时的设计方法
当锥壳变径段较短时,应考虑锥壳与大、小端圆柱壳相连接时边缘效应耦合,此时控制锥壳变径段设计厚度(即Q值)的准则是式(26),(29),塑性极限状态下小端圆柱壳和锥壳小端先发生塑性流动,而大端圆柱壳仍为弹性状态,该处一次加二次应力强度满足准则式(28)的要求。应用下式设计:
(31)
此时Di=Dis=2R1-t。
图12,13示出式(31)中的Qs值的两例,由α,DiL/Dis和p/Sm值读取。边缘效应耦合时,按本文所设计结构的安全裕度见后续第(二)部分。

图12 α=45°时考虑锥壳变径段大、小端边缘效应耦合作用时的Qs值

图13 α=55°时考虑锥壳变径段大、小端边缘效应耦合作用时的Qs值
6 结论
本文基于弹性薄壳理论,给出了内压作用下锥壳大、小端与圆柱壳相连接的结构的精确解,并进行了有限元法的数值验证。数值验证算例说明,现有压力容器规范所采用的薄壳简单边界效应解在锥壳半顶角α较大、锥壳较短时有较大误差。据此提出了以锥壳精确解为基础的设计方法,给出了锥壳大端连接圆柱壳结构的设计方法,并给出了锥壳变径段较短、其两端边缘效应互相耦合时的分析设计方法。利用理想弹塑性轴对称体小变形有限元法对所设计的结构进行了塑性极限分析,显示它们均有足够的安全裕量。对于该设计方法所得锥壳大端与圆柱壳连接的结构,用理想弹塑性大变形三维有限元法进行分析,显示这些结构的破坏模式仍是过大的塑性流动,即设计曲线所给范围内的结构不会发生内压失稳破坏,从而保证了设计方法的可靠性。本文还提出锥壳与圆柱壳连接处采用修磨焊缝至半径为r0≥δr的过渡圆角的方法,在锥壳半顶角α≤60°时证明仍可有效降低连接处的应力集中,将不带折边过渡段的锥壳与圆柱壳连接结构设计方法扩大至α≤60°的范围。

