尺寸效应对固支直杆弯曲小试样蠕变性能评价的影响

，，，，

(华东理工大学 机械与动力工程学院 承压系统与安全教育部重点实验室，上海 200237)

0 引言

蠕变是高温设备最主要的破坏形式[1]。因此，准确测量材料的蠕变性能对预测高温设备剩余寿命并进行安全评价具有重要意义。单轴拉伸试样因其体积大，易对设备造成较大损伤[2]，应用受到局限，尤其对于一些在高技术领域中应用的薄板、薄壁管等微小、紧凑结构，更无法提供足够的材料以取样进行试验。为响应高参数装备高效率、长寿命运行的发展需求，小尺寸单轴拉伸、小冲杆[3-4]、压痕蠕变[5-6]、三点弯曲[7-8]、悬臂梁[9]等多种小试样蠕变技术应运而生。但是，小尺寸单轴试样制造复杂，且安装时易产生偏差；压痕蠕变无法得到蠕变第三阶段参数；小冲杆受力复杂[10]，与单轴关联问题尚不统一；简支三点弯与悬臂梁的约束较小，难以得到韧性材料的断裂数据。这些固有的缺点限制了小试样技术在工程领域的进一步应用。

固支直杆弯曲小试样[11]因试样结构简单、受力简单、能得到断裂数据等特点，在在役和非在役设备材料性能测试评价方面具有潜在的优越性，近年来备受学者们的关注。庄法坤[11]基于梁弯曲理论，提出了小变形范围固支直杆弯曲蠕变变形本构，并与传统单轴蠕变进行了关联；白钰[12]通过引入系数λ对固支直杆蠕变小变形本构进行了修正，并指出λ=4时该修正的本构与单轴蠕变关联性更好；秦宏宇[13]通过引入全局变形理论，建立了大变形下固支直杆位移应变转换公式；Zhuang等[14]利用有限元模拟，得出了摩擦对固支直杆小试样蠕变测量精度的影响规律；Tu等[15]分析了大变形对蠕变关联式的影响，提出了采用临界载荷方法控制大变形效应。上述研究都是针对固支直杆小试样的本构以及与传统单轴试样的关联，并未考虑试样的结构与尺寸。然而，由于小试样相比于传统试样十分微小，其尺寸的变化势必影响到所测材料蠕变性能的真实性和准确性[16]，而目前的研究也未表明试样尺寸的变化是否会影响理论公式的准确性。因此，为建立固支直杆小试样蠕变试验标准，便于其蠕变试验技术在工程中的推广应用，开展试样尺寸效应对固支直杆弯曲蠕变性能影响的研究工作具有重要意义。

本文基于固支直杆小试样梁弯曲本构模型，利用ABAQUS有限元模拟软件，对不同横截面尺寸比例、不同固定端结构尺寸的试样的蠕变性能进行数值模拟分析，研究试样的尺寸效应对固支直杆蠕变性能评价的影响，并与单轴试验结果对比，获得较优的结构形式及几何尺寸，为固支直杆弯曲小试样蠕变试验标准化提供数据支持。

1 固支直杆弯曲小试样理论模型

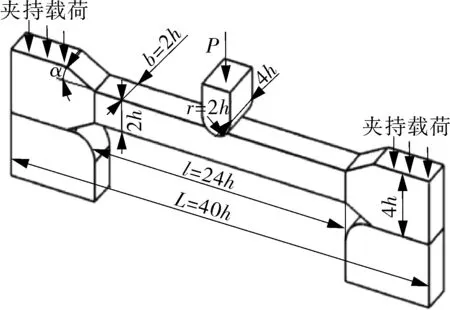
固支直杆弯曲小试样的蠕变试验示意图如图1(a)所示。试样两端被上下夹具夹持，进行固支约束后放置于高温炉中，通过对压头施加恒定载荷将力传递到试样上，压头作用于试样跨距中心处。

(a)试验示意图 (b)弯矩图

图1 固支直杆弯曲小试样蠕变模型

根据常用的固支直杆弯曲小试样小变形理论[13]，将固支直杆弯曲小试样简化为两端受附加弯矩的简支三点弯试样，弯矩如图1(b)所示。假设材料满足平面弯曲假设、正向纤维间无正应力假设与小变形假设，忽略截面上的剪力作用，将横力弯曲问题简化为纯弯曲问题。可得固支直杆弯曲的有效跨距点x*和固定端处弯矩M0[11]为：

x*=l/4

(1)

M0=-Pl/8

(2)

由此可得试样的弯矩方程为：

(3)

假设材料满足Norton蠕变方程：

(4)

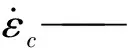
σ——应力，MPa；

B，n——材料参数。

当梁弯曲处于小变形阶段时，由几何关系可得：

εc=y/ρ

(5)

式中y——试样横截面上的纵坐标;

ρ——挠度曲率。

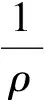
(6)

联立式(5),(6)，可得：

εc=d″y

(7)

将式(7)代入Norton蠕变方程(4)中，得到应力与挠度的关系：

(8)

在固支直杆截面上对上式积分，获得弯矩方程为：

(9)

将弯矩方程(3)、应力方程(8)代入方程(9)，可得固支直杆试样的挠曲线微分方程：

(10)

固支直杆挠曲线方程边界条件为：

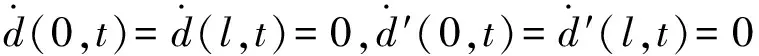
(11)

(12)

对式(10)进行二次积分，并将边界条件式(11)，(12)代入，当x=l/2时，可得试样中心位移速率为：

(13)

将式(13)与Norton本构对照后，可得固支直杆与单轴蠕变的等效应力和等效应变速率：

(14)

(15)

2 有限元模型及计算方法

本文采用ABAQUS-6.13进行数值模拟计算。试样的有限元模型如图2所示，试样为矩形截面直杆试样，定义试样厚度2h=1 mm、宽度b=2 mm、总长L=20 mm、有效跨距l=12 mm、压头半径r=1 mm。蠕变本构采用Norton方程(见式(4))。研究材料为A7N01铝合金，其350 ℃下的力学性能与蠕变参数如表1[11]所示。

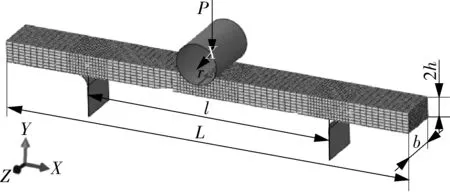
图2 固支直杆弯曲小试样有限元模型

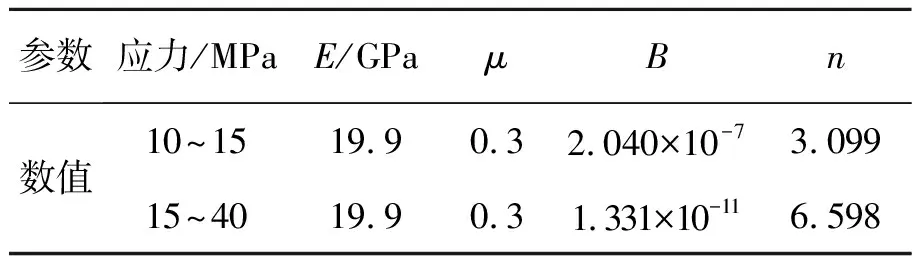
参数应力/MPaE/GPaμBn数值10～1519.90.32.040×10-73.09915～4019.90.31.331×10-116.598

试样两端面直接固定(U1=U2=U3=0)。恒定载荷P通过圆柱形压头施加在试样中心，约束压头除y方向以外的全部自由度。根据文献[11]的研究结果，压头与试样间的接触形式为面-面接触，摩擦系数对稳态位移速率影响较小，可取f=0.3。试样网格选用三维八节点线性减缩积分单元类型(C3D8R)，为提高计算精度，对试样压头中心和固定端等变形较大位置的网格进行加密。对试样进行网格无关性验证，载荷P=2N，图3示出不同数量网格的时间-位移曲线，各曲线200 h的蠕变位移量如表2所示。可以看出，当网格数量达到2 400个单元时，随着网格数量的增加，位移-时间曲线基本不再变化，故将模型划分为2 400个单元、3 234个节点。由于仅研究小变形下的蠕变过程，故关闭几何非线性。

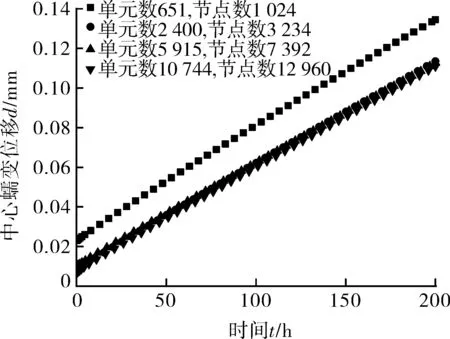
图3 有限元模型网格无关性验证

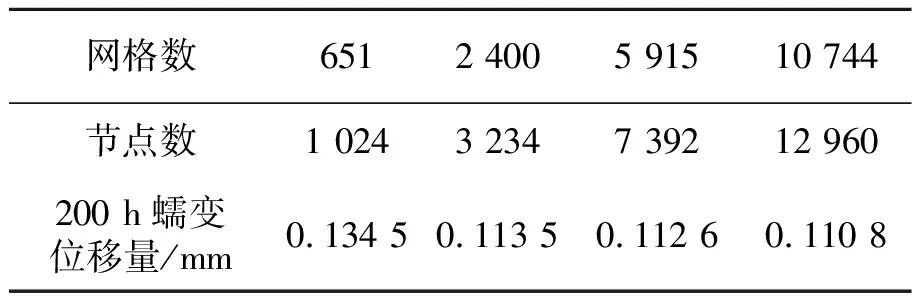
网格数6512 4005 91510 744节点数1 0243 2347 39212 960200 h蠕变位移量/mm0.134 50.113 50.112 60.110 8

3 试样尺寸对蠕变稳态位移速率的影响

3.1 试样高跨比的影响

由图4所示三点弯试样受力简图可知，试样受集中载荷发生横力弯曲时，横截面内既有正应力又有切应力。当试样跨距同厚度满足一定条件成为细长梁时，切应力的影响可以忽略，此时横力弯曲问题简化为纯弯曲问题[17]，满足建模过程中的假设。

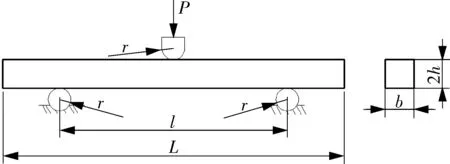
图4 三点弯试样示意

由材料力学知识，三点弯梁横截面上的最大切应力与最大正应力之比为：

(16)

当2h/l=1∶10时，最大切应力仅为正应力的10%，可以忽略。考虑固支直杆弯曲小试样固定端约束较大，故选取2h/l=1∶12。

3.2 试样宽厚比的影响

目前用到的固支直杆弯曲小试样蠕变本构在推导过程中，没有对试样横截面宽厚比进行假设。通过数值模拟研究发现，当等效应力不变时，稳态位移速率模拟结果与理论值的相对误差随试样横截面宽厚比变化较大，如表3所示。由此可见，试样横截面宽厚比对固支直杆弯曲小试样蠕变本构的有效性和准确性具有决定性的作用。

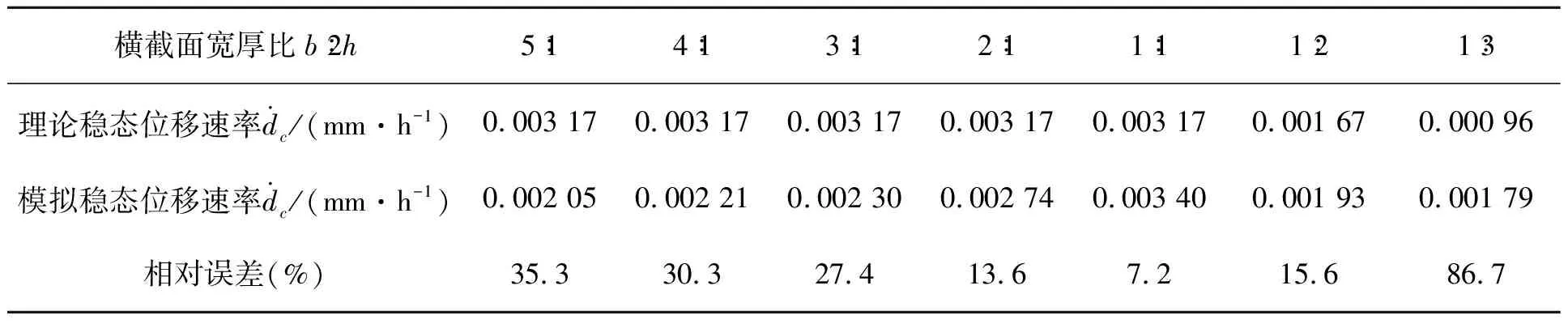
表3 等效应力为12 MPa时不同宽厚比的稳态位移速率相对误差

建立多组横截面宽厚比不同的固支直杆弯曲小试样模型，分别进行4个等效应力(10，12，15，20 MPa)的蠕变模拟，并采用下式计算其模拟结果的相对误差:

(17)

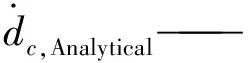
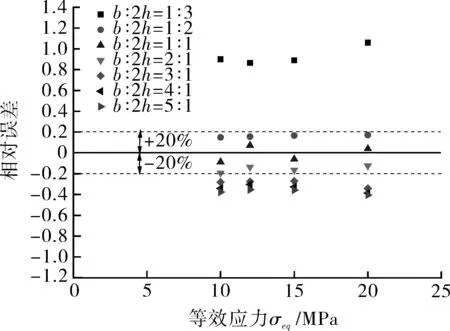
图5 不同宽厚比的固支直杆弯曲小试样的

不同宽厚比的模拟结果的相对误差如图5所示。可以看出，当横截面宽厚比b∶2h在0.5～2时，模拟得到的稳态位移速率与理论值的偏差在±20%以内；其余横截面宽厚比的相对误差都较大，说明此时试样已不满足梁弯曲本构的基本假设。综上所述，试样横截面宽厚比应在0.5～2范围内。

4 固定端结构对蠕变的影响

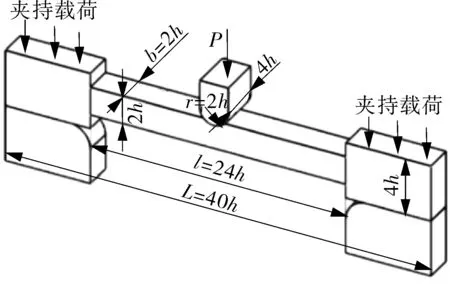
为了提高试验精度，需要合理设计试样固定端结构。图6(a)示出固定端直接与一个固定平面相接的理想结构，难以在试验中实现。根据实际加工制造技术需求，设计了如图6(b)所示的过渡段的试样固定端结构型式，在试样有效长度l后端设置倾斜角α的过渡段。当α=0°时，固定端厚度与试样厚度一致(见图6(c))，即2h=1 mm；当α=90°时，固定端为直角过渡(见图6(d))，厚度取为4h=2 mm。横截面宽厚比b∶2h=1∶1。

(a)理想型

(b)0°<α<90°

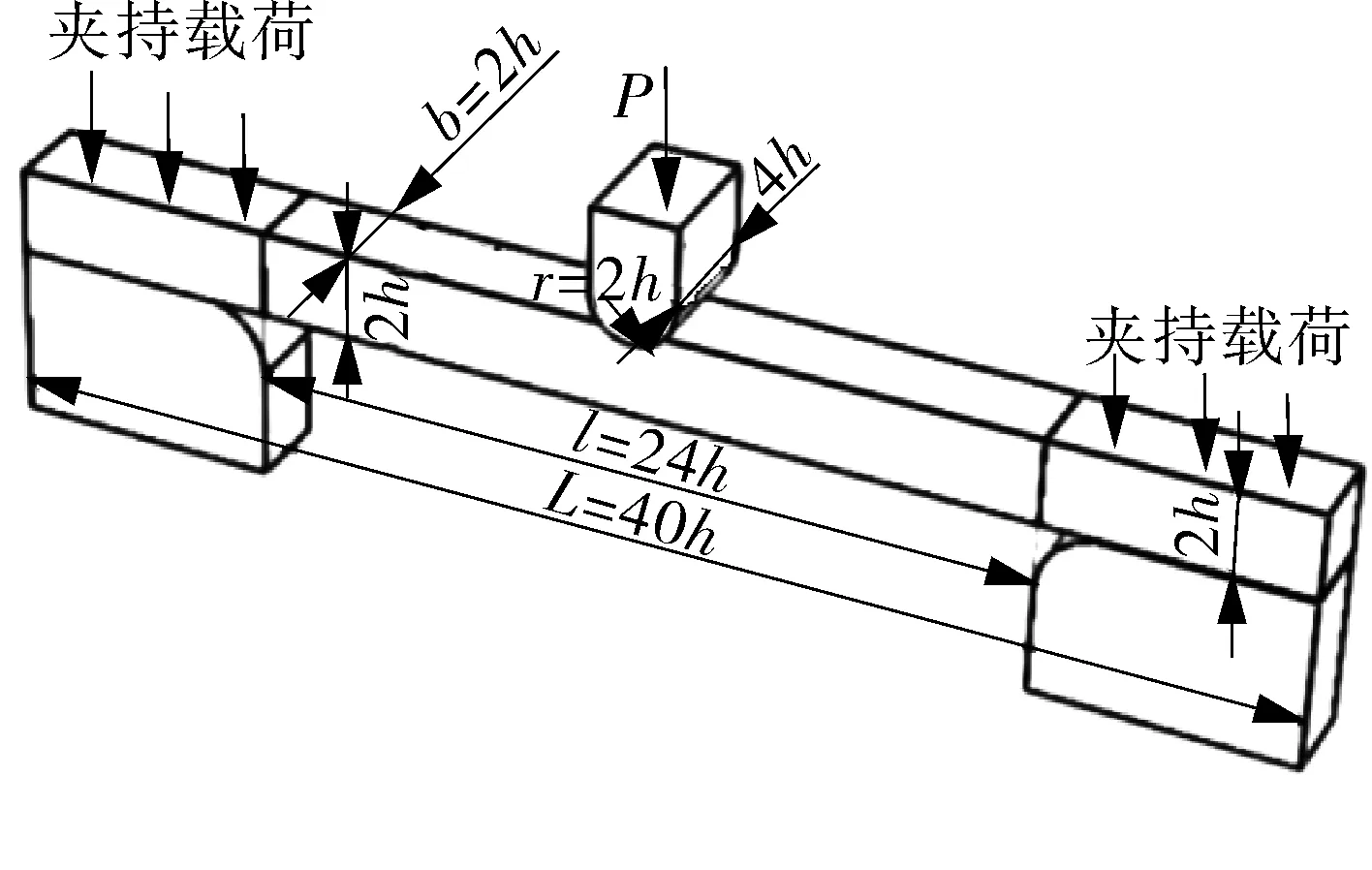
(c)α=0°

(d)α=90°

图6 固支直杆弯曲小试样固定端结构

4.1 固定端倾斜角对试样横截面应力的影响

服从Norton蠕变定律的材料，试样横截面上的应力[18]为：

(18)

对于矩形截面梁，截面的惯性矩为：

(19)

通过对比不同倾斜角横截面最大应力与理论值的相对误差，可以得到固定端倾斜角对试样力学响应的影响。横截面最大应力的相对误差通过下式计算得到：

(20)

式中σ1，Numerical——根据有限元得到的横截面最大拉伸应力；

σ1，Analytical——由式(18)计算得到的横截面最大拉伸应力。

表4列出了不同倾斜角的试样横截面最大拉伸应力相对误差。

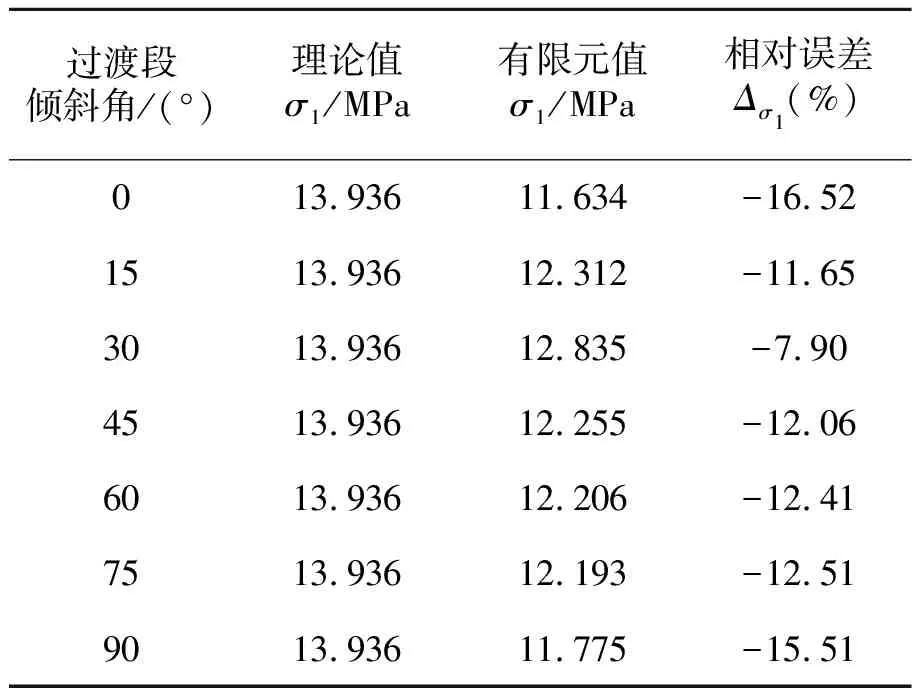
表4 不同倾斜角的试样横截面最大拉伸应力相对误差

从表4可以看出，倾斜角为30°时，横截面最大拉伸应力与理论值的相对误差最小，在10%以内；倾斜角为0°和90°时，相对误差均在15%以上；其余倾斜角的相对误差为10%～15%。因此，当过渡段倾斜角在15°～75°时，横截面的最大拉伸应力与理论预测更接近，可以更好地描述固支直杆弯曲小试样蠕变的力学响应。此外，当α≠0°时，试样的固定端与跨距间存在过渡段，可以避免夹持应力对试样蠕变性能的影响。

4.2 固定端倒角对蠕变稳态位移速率的影响

当试样固定端的倾斜角α≠0°时，其夹持部位与试样跨距段的连接处存在结构不连续，须通过加工倒角以消除应力集中，如图7所示。但由于试样尺寸小，倒角的加工精度难以保证，故需研究不同倾角时，倒角加工误差对试验结果影响情况，以选取合理的固定端倾角。

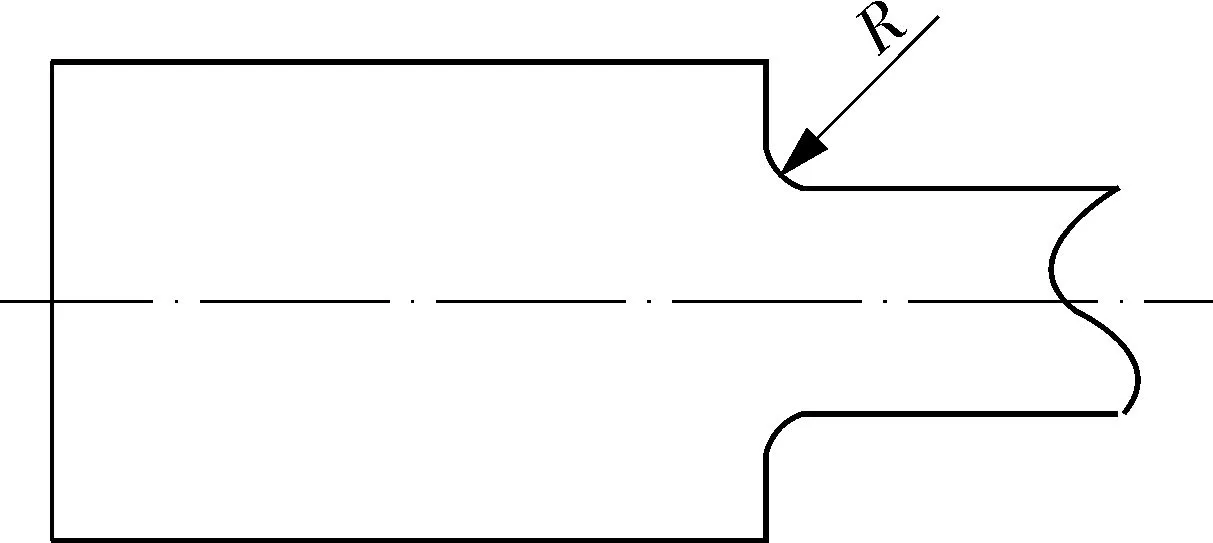
(a)α=90°

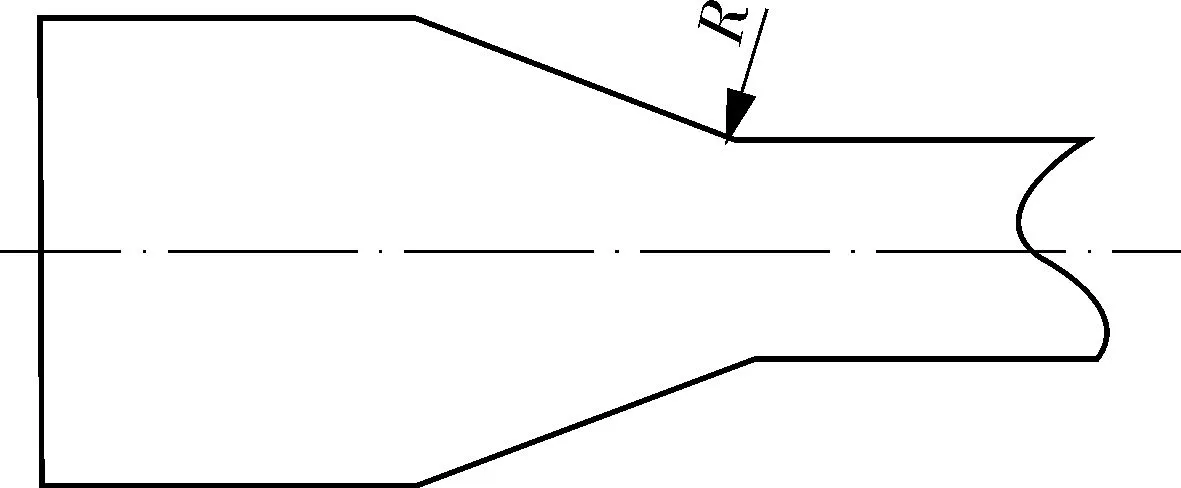
(b)0°<α<90°

在改变固定端倒角的半径后，不同倾斜角试样的位移-时间变化曲线如图8所示。可以看出，随着倒角半径r增大，载荷点的位移量逐渐降低。进一步发现，在200 h时，不同倾斜角试样随倒角半径变化的位移偏差量也不同。当倾斜角为30°时，其最大位移偏差量仅为2.3%；而当倾斜角为90°时，其最大位移偏差量为21.6%。

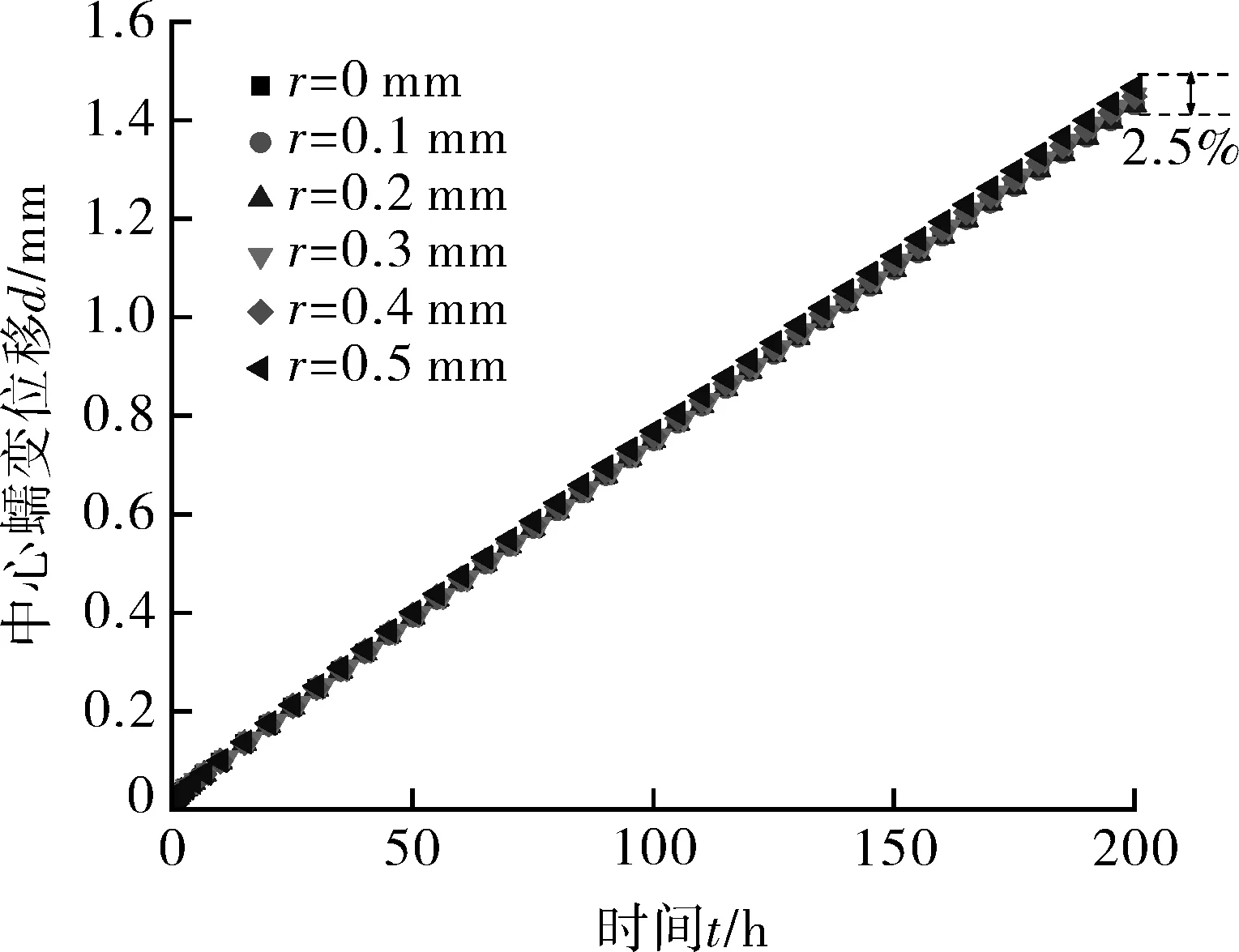
(a)α=15°

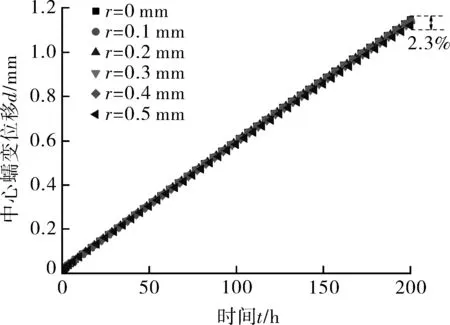
(b)α=30°

(c)α=45°

(d)α=60°

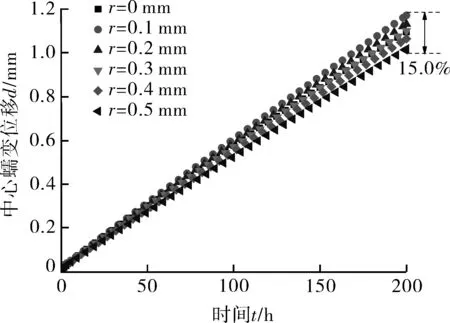
(e)α=75°

(f)α=90°

图8 固定端倒角半径对位移-时间曲线的影响

固定端倒角半径r对载荷点稳态位移速率的影响如图9所示。可以看出，当试样倾斜角α≤45°时，载荷点的稳态位移速率基本不受倒角半径变化的影响；当α>45°时，倒角半径变化对试样稳态位移速率的影响随着试样倾斜角的增大而增大。因此，过渡段倾斜角大于45°时，倒角半径会显著影响试样稳态位移速率，进而对蠕变试验测试结果的有效性产生较大影响。根据式(21)，(22)计算出不同倾斜角试样的稳态位移速率随固定端倒角半径变化的最大与最小偏差，其结果列于表5。

(21)

(22)

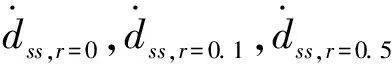
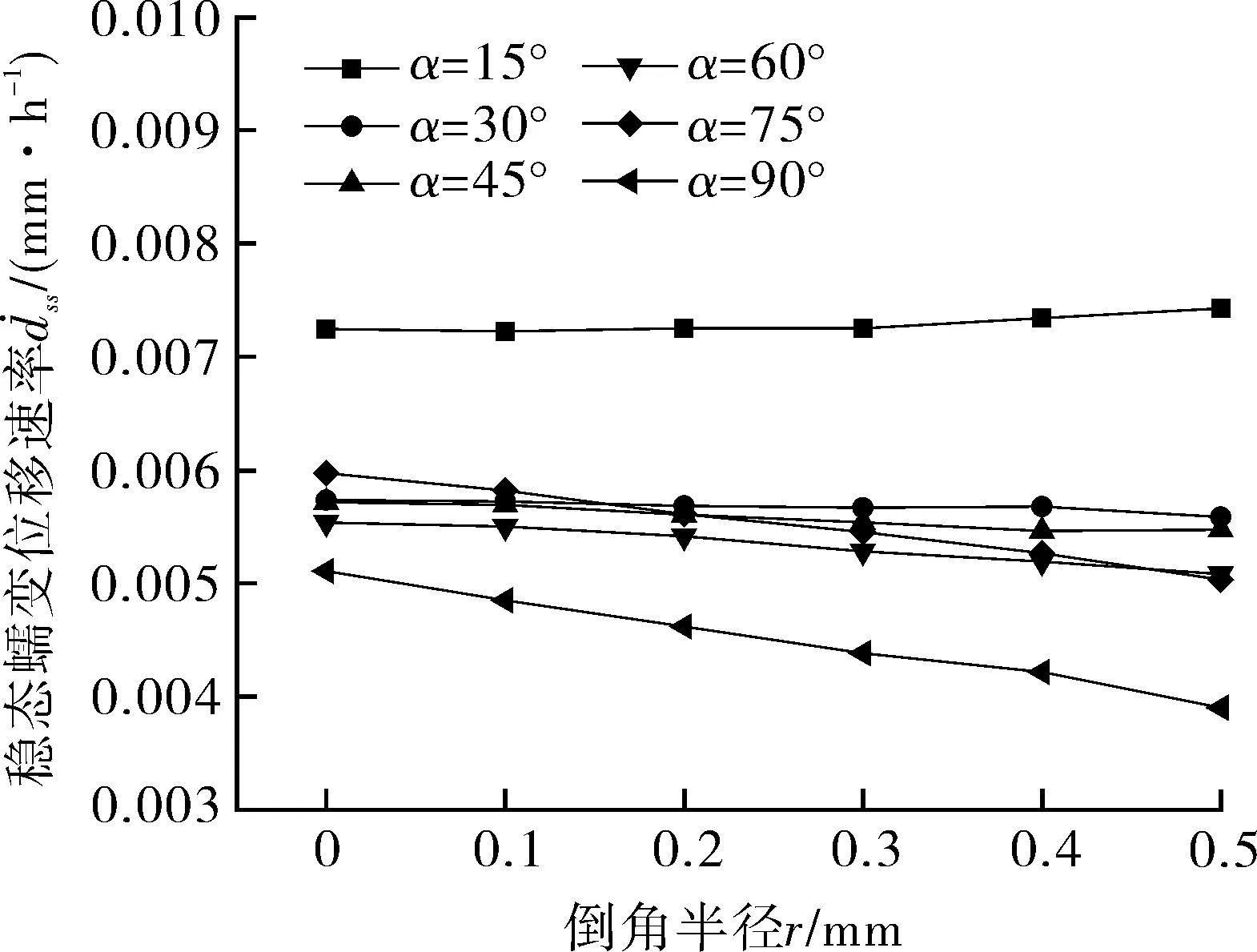
图9 固定端倒角半径对稳态位移速率的影响

综上所述，倒角半径增大会降低载荷点的稳态位移速率，进而影响其蠕变位移量。其影响程度取决于倒角半径变化的大小以及试样固定端的倾斜角角度。倾斜角在15°～45°时可明显降低倒角半径变化对蠕变的影响，因此固定端的倾斜角推荐值为15°～45°。

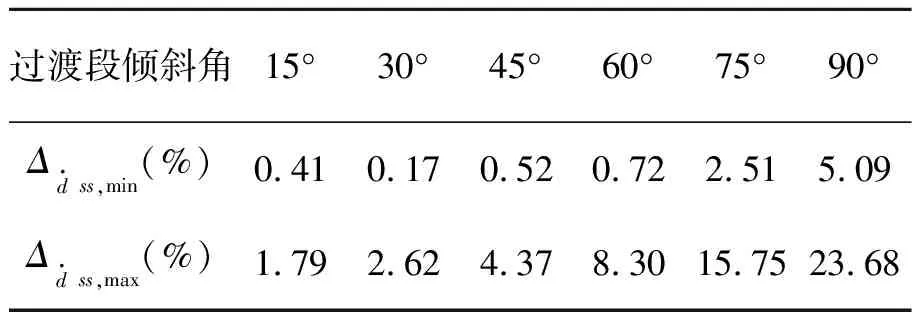
表5 不同倾斜角试样的稳态位移速率随固定端倒角半径变化的最大与最小偏差

5 分析与讨论

通过上述分析可知，试样横截面的宽厚比变化会对蠕变稳态位移速率产生影响。改变试样过渡段倾斜角的大小，会导致试样的实际有效跨距发生变化，进而也会影响试样的稳态位移速率。因此，需要综合考虑横截面宽厚比和过渡段倾斜角对蠕变的影响，从而得出与单轴试验结果关联度最好的试样类型。

(a)b∶2h=2∶1

(b)b∶2h=1∶1

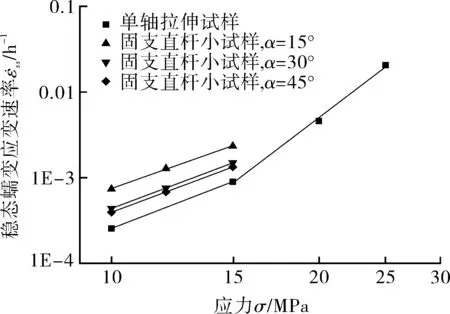
(c)b∶2h=1∶2

图10示出双对数坐标下不同横截面宽厚比、不同过渡段倾斜角试样的稳态应变速率与应力的关系，并与单轴试验结果进行对比。可以看出，对于不同的应力水平阶段，稳态蠕变速率与应力之间的关系并不是保持不变的，这是因为随着应力水平的增加，材料的蠕变机制发生了变化[12]。将低应力区域放大(如图11所示)，可以更清楚地看出试样的稳态应变速率随应力的变化关系受横截面宽厚比和过渡段倾斜角的影响较大。

(a)b∶2h=2∶1

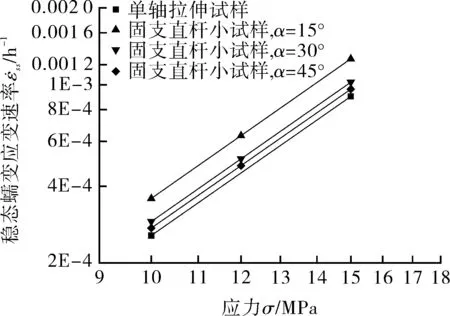
(b)b∶2h=1∶1

(c)b∶2h=1∶2

不同结构参数的试样模拟结果与单轴试验的最大误差如表6所示。可以看出，横截面的宽厚比b∶2h=2∶1、过渡段倾斜角为30°以及横截面的宽厚比b∶2h=1∶1、过渡段倾斜角为45°的试样与单轴试验的吻合度最高。当试样横截面的宽厚比b∶2h=1∶2时，各个过渡段倾斜角的稳态蠕变应变速率与单轴试验的误差过大，因此，该固定端结构试样的横截面宽厚比不应取为1∶2。

6 结论

本文基于有限元方法，模拟分析了不同试样横截面宽厚比和不同固定端结构下固支直杆弯曲蠕变性能，并与单轴试验结果对比，获得了两种与传统蠕变试验关联性最好的试样结构。

表6 不同结构参数的试样与单轴试验对比误差

主要结论如下。

(1)当横截面的宽厚比b∶2h在0.5～2范围时，其稳态位移速率的模拟结果与理论值相对误差在±20%以内，所以试样横截面的宽厚比不应该超出此范围。

(2)当过渡段倾斜角在15°～75°时，横截面的最大拉伸应力与理论预测最接近，可更好地描述固支直杆弯曲小试样蠕变的力学响应，且当过渡段倾斜角在15°～45°时可以明显降低倒角半径变化对蠕变试验的影响。因此，过渡段倾斜角推荐选择15°～45°。

(3)经过与单轴试验的稳态应变速率-应力曲线对比可知，当横截面的宽厚比b∶2h=2∶1时，选择过渡段倾斜角为30°的试样最优；当横截面的宽厚比b∶2h=1∶1时，选择过渡段倾斜角为45°的试样最优。