衍射时差法(TOFD)技术的测量误差分析
, , ,, ,志平
(1.合肥通用机械研究院特种设备检验站有限公司,合肥 230031;2.上海石化设备检验检测有限公司,上海 200540)
0 引言
利用衍射时差法(TOFD)技术对缺陷尺寸的测量包括缺陷深度、自身高度和长度的测量,因此测量误差也包括了缺陷深度、缺陷自身高度和长度的测量误差。
TOFD技术的尺寸测量优势在于把A扫波形和B扫图像结合起来。B扫图像帮助识别缺陷,包括缺陷形状、走向、相位、上下(高度)及左右(长度)端点位置及分布的密集程度等;而A扫波形能更精确地确定测量点的位置。此外,TOFD技术依据端点衍射法来确定缺陷的尺寸,因此与脉冲反射法超声检测相比有更明显的优势[1]。一般来说,TOFD技术对缺陷深度测量误差的平均值大约为1 mm[2];对缺陷高度的测量,由于一般情况下上下端点的偏差是同向的,这样高度的测量误差则能做到比深度误差要小得多。定点监控裂纹时,自身高度测量误差可达0.1 mm[3];对于缺陷长度的测量,其误差和脉冲反射法超声检测相比优势不大[4],但如通过特殊处理方法(如合成孔径技术(SAFT)等),可大大提高长度测量精度[5-6]。鉴于篇幅所限,本文主要重点讨论深度和高度测量误差。
1 TOFD原理及深度和高度测量误差影响因素
TOFD技术的原理是通过一收一发探头对来测量缺陷上下端点衍射信号的[7],从而对缺陷进行定位和定量(见图1)。
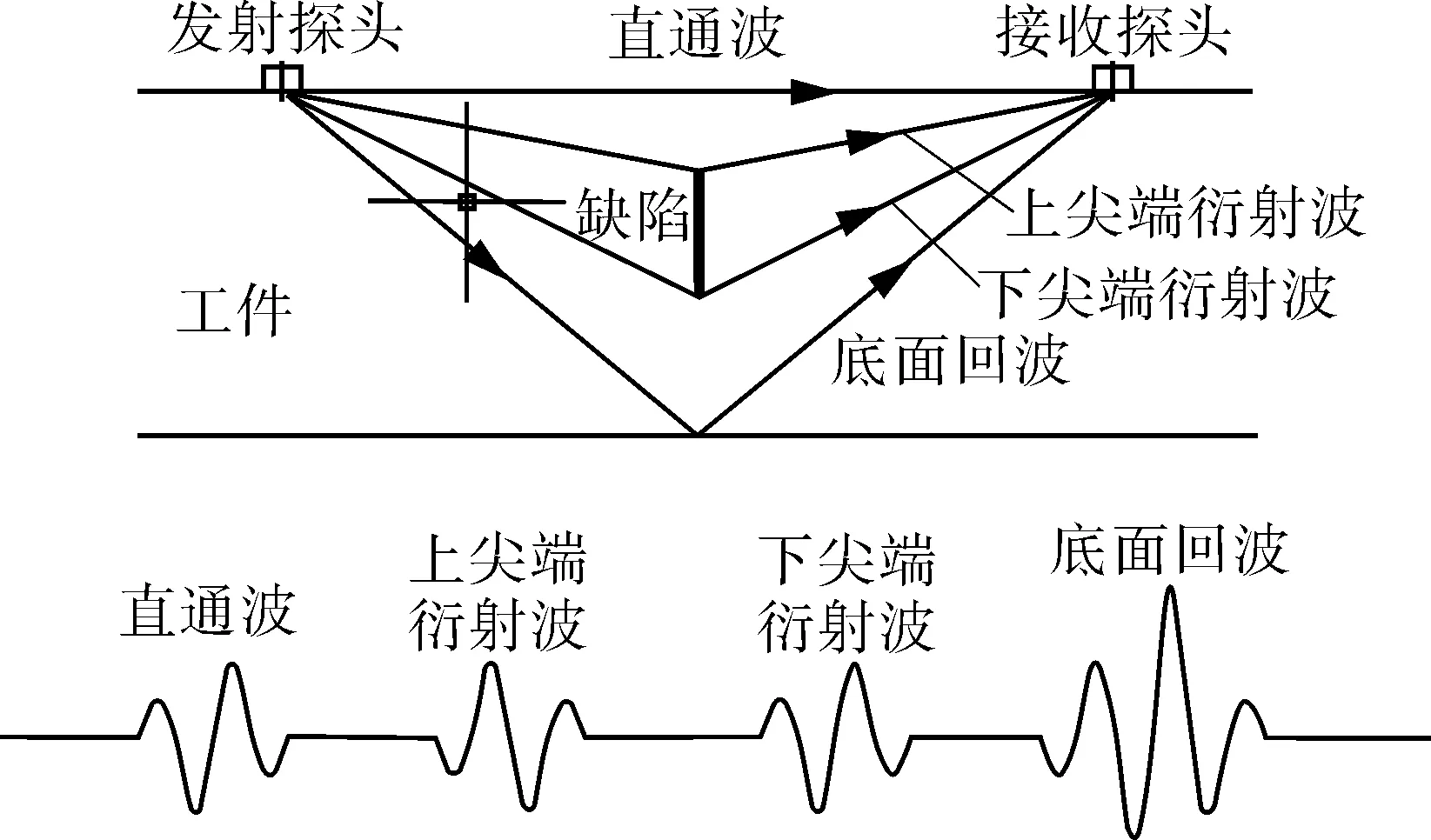
图1 衍射时差法超声检测原理示意
由于TOFD技术是利用衍射信号传输的时间和相对某已知信号(如直通波、人工反射体回波或底面回波等)的传输时间差来测定衍射点深度位置的,而缺陷高度又是通过测量上下端点衍射信号传输时间差来确定的,因此,导致TOFD技术产生深度和高度测量误差归根结底就是传输时间的误差。
一般引起深度和高度测量误差的主要影响因素有:(1)轴偏移(缺陷与探头对的对称性);(2)探头对间距(PCS)的变化;(3)耦合剂厚度;(4)检测面的平整度;(5)声速变化;(6)模拟信号数字化处理的时间间隔;(7)检测面曲率。
2 缺陷深度和高度测量误差基本公式
2.1 缺陷深度测量误差
假设缺陷位于两个探头中间的对称位置(见图2),则从发射探头到接收探头的整个声波传播时间t由下式得出:
(1)
式中t——声波自发射探头到接收探头传播的时间,μs;
s——探头对间距(PCS)的一半(见图2),mm;
d——缺陷深度(见图2),mm;
c——工件纵波声速,mm/μs;
t0——时间t扣除工件中传播的时间后的时间,μs,即自仪器反射脉冲信号开始,经过发射探头到工件接触面,再到接收探头,最后回到仪器的传输时间之和。
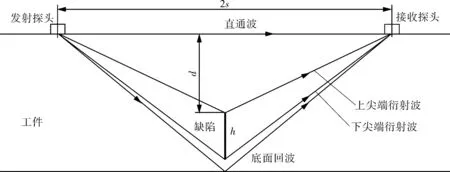
图2 TOFD探头布置示意
式(1)整理后,缺陷深度为:
(2)
求对上式关于d和t的微分,即传输时间的误差引起深度的误差,或者说深度测量误差δd可以由时间误差δt来表示,即:
2dδd=2(c/2)2(t-t0)δt
(3)
用式(1)替代上式中的t:
(4)
上式即为缺陷深度测量误差的基本公式。可以看出,随着深度d的减小,误差δd迅速增加,即缺陷越接近检测面,深度测量越不准;另外还可以看出,减小探头中心距s有助于减小深度测量误差,或者说减小探头中心距可以提高缺陷检测的分辨力。但这样会造成扫查的覆盖范围减小,降低了检测效率。
2.2 缺陷高度测量误差
按图2所示,缺陷上尖端深度为d,缺陷自身高度为h,即缺陷下尖端深度为d+h,则有:
缺陷上尖端d处的深度测量误差为
缺陷下尖端d+h处的深度测量误差为
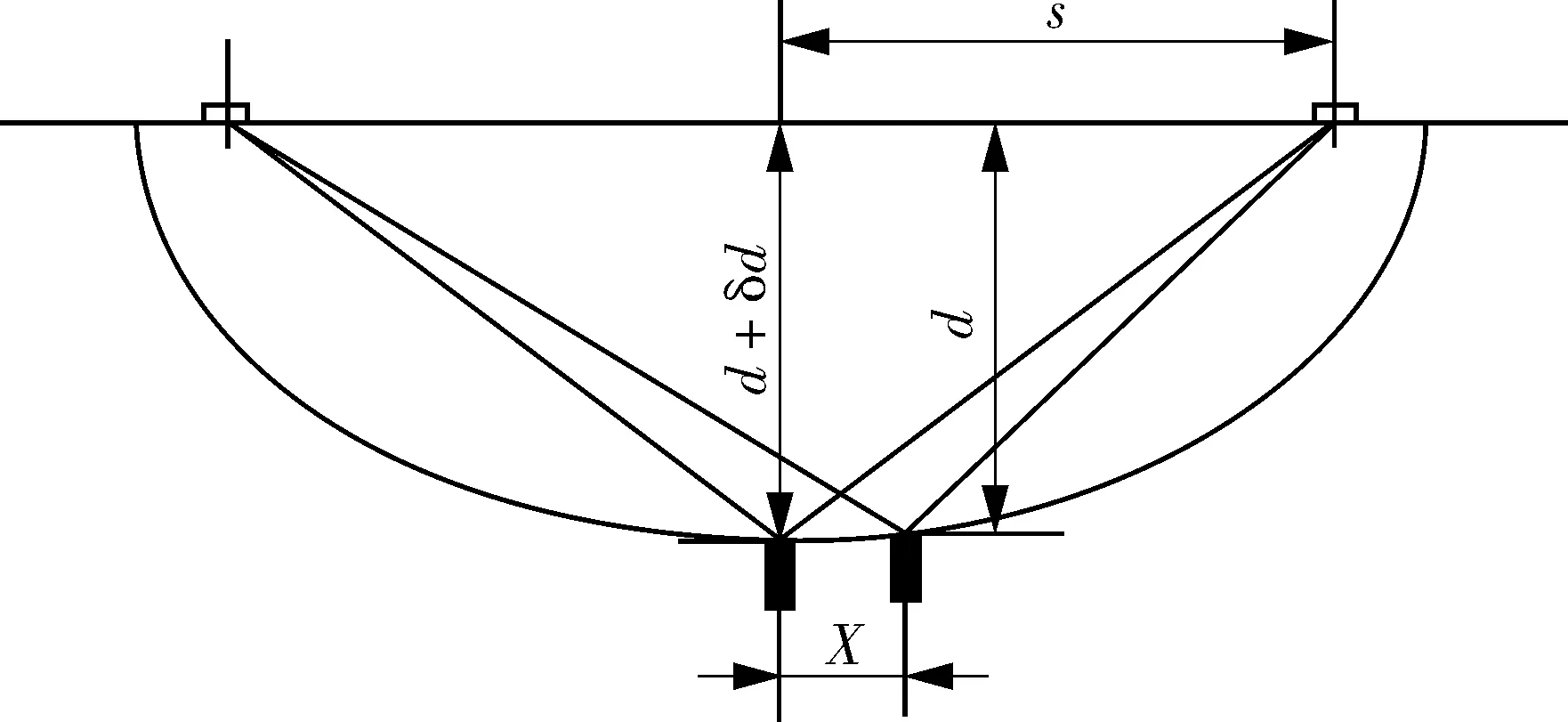
由于深度测量误差是同方向的,并考虑到h< (5) 公式(5)即为缺陷自身高度测量误差的基本公式。 例如,在进行TOFD检测时,s=50 mm,声速为5.95 mm/μs,时间测量误差δt=0.02 μs,缺陷自身高度h=2 mm。当缺陷深度为20 mm,得到的深度误差δd=0.16 mm,自身高度误差δh=-0.01 mm。可见自身高度误差的大小(绝对值)要远小于深度测量误差。 非平行扫查时,如果缺陷不是位于两探头之间的中心位置,会导致深度测量出现误差。如图3所示,设缺陷实际深度为d,偏离两个探头中心为X,则测量深度为d+δd。 图3 轴偏移引起的深度误差示意 通常,轴偏移引起的深度测量误差可以用2种方法计算。 (1)同深度缺陷在轴偏移量为X时与处在探头对中心位置的缺陷传输时间差δt: (6) 再利用式(4),可得深度偏差: (7) (2)利用传输时间相等原理,即处于探头对中心位置深度为d+δd与偏移量X、深度d的两缺陷的传输时间相等,则有几何关系式: (8) 对上式求解得深度测量误差(当轴偏移量较小时,忽略二阶分量): δd=X2d2/[2(s2d+d3-X2d)] (9) 式(8)适用于任何情况下的深度或深度误差计算。式(7)和(9)仅适用于偏移量不大的情况,但对于一般焊接接头检测来说,此两式的计算精度已足够。 例如,对于厚度50 mm的焊缝试件,其纵波声速c=5.95 mm/μs,PCS=100 mm,试件中有一缺陷,深度40 mm,可以用式(7)或式(9)计算出该缺陷偏离探头对中心位置为5,10,20 mm时的深度测量误差δd分别为0.1,0.5,2.0 mm。 探头对间距的误差主要来源于楔块前沿距离测量不准确或PCS测量不准确。 探头对间距的误差δs引起传输时间的误差δt,而此时缺陷实际深度并没有改变,仪器设定的PCS(即2s)也没有改变,这样就使得缺陷显示(或测量)深度值发生了改变,从而带来了深度测量误差。 对式(1)求微分(t和s为变量),可得: (10) 将上式代入式(4)(由s变化引起传输时间t的变化,而最终导致深度的变化),可得: δd=sδs/d (11) 由式(11)可见,探头对间距的误差δs对深度测量产生影响,对越接近表面的缺陷,深度测量误差越大。例如s=50 mm,误差δs=1 mm,如果缺陷深度20 mm,则得到误差δd=2.5 mm;但如果缺陷深度10 mm,得到的误差δd=5 mm。 其实讨论未进行深度校准时探头对间距误差引起的深度测量误差意义不大,因为实际检测时,一般在检测前都需要利用直通波、底面波信号或对比试块上的人工反射体来进行深度校准,因此本文主要讨论仪器深度校准后的误差。另外,虽然探头对间距的误差δs对深度测量准确性影响很大,但是对缺陷高度测量影响很小。 由式(11)可得缺陷上尖端的深度测量误差为: δdd=sδs/d 缺陷下尖端的深度测量误差为: δdd+h=sδs/(d+h) 由于深度测量误差是同方向的,故缺陷高度测量误差为: δh=δdd+h-δdd=-shδs/d(d+h) (12) 例如s=40 mm,误差δs=1 mm,并且假定h=2 mm,当缺陷深度20 mm,则得到的高度误差δh=-0.2 mm;当缺陷深度40 mm,得到的高度误差δh=-0.06 mm。 由前文可知,探头对间距的偏差会导致深度测量的误差,然而,如果使用已知反射体的回波信号进行深度校准,就能使这个测量误差大为减小。其实在编制检测工艺时,当选择好检测参数(仪器设备、探头、楔块、PCS、试块、楔块前沿测试的数据等)后,检测前都要对仪器进行深度校准。 (1)使用已知深度反射体回波校准。 缺陷深度d的衍射点的信号传输时间: 已知深度为H的反射体回波传输时间: 因此这两个信号的声程差为: (13) 对上式t和s求微分,另外考虑到同时采用已知反射体进行深度校准,故δtH=0,此时有δt=δtd,对式(13)求微分,得到: (14) (15) (2)使用直通波校准。 当使用直通波校准时,即H=0,则式(15)可变为: (16) 上式即为使用直通波校准时,由PCS变化引起的深度测量误差。 (3)使用底面波校准。 当使用底面波校准时,即H=D(设试块厚度或工件厚度为D),则式(15)可变为: (17) 上式即为使用底面波校准时,由PCS变化引起的深度测量误差。 (4)同时使用直通波和一次底波校准。 使用直通波和底面波同时校准,此时不仅对楔块延时进行校准,还对声速进行校准,也就是说,工件声速c也是变量。 底面反射波传输时间: 直通波传输时间: tl=2s/c+t0 缺陷信号与直通波信号的传输声程差: (18) 缺陷信号与底面反射信号的传输声程差: (19) 对式(18),(19)中的t,s和c求微分,另外考虑到同时采用直通波和底波进行深度校准,故δtl和δtB均等于0,此时δt=δtd,解联立方程得到: (20) 将上式代入式(4),可得使用直通波和底面回波同时校准时的深度测量误差: (21) 例如,对厚度60 mm的工件,设定PCS=120 mm,δs=1 mm(即PCS偏差2 mm),使用直通波和底波同时校准深度,则可得到深度为0,30,60 mm处的测量误差分别为0,-0.05,0 mm。 表1列出s=50 mm,H=20 mm(人工反射体深度),D=40 mm,δs=1 mm,c=5.95 mm/μs,使用不同类型校准情况下的深度测量误差比较。 表1 不同类型校准情况下PCS误差带来的深度测量误差 (5)试验验证。 通过试验,可以验证在未进行深度校准和使用直通波进行深度校准两种情况下,探头对间距误差引起不同深度反射体的深度误差情况,并与理论计算进行对比。 设PCS=100 mm,表2,3分别列出实际探头对间距为102 mm和105 mm时的深度测量数据和误差分析。 表2 实际探头对间距为102 mm时不同深度反射体实测数据和误差分析 mm 表3 实际探头对间距为105 mm时不同深度反射体实测数据和误差分析 mm 通过上述试验数据和理论计算值的比较可以看出,探头对间距(PCS)误差引起的深度测量误差的理论分析是基本正确的,包括误差数值和方向(正负值)。 试验误差主要是由于在扫查架上固定探头时,其间距(PCS)仍会有偏差;另外,所用反射体在不同试块上,尽管材质一样,但声速也会有一定差异,也会带来误差。 TOFD检测和常规超声检测一样需要耦合剂,目的是使声波通过耦合层到达工件内部,因此耦合层厚度的大小或变化会影响声波传输时间。也就是说,耦合层厚度的变化会给缺陷深度测量带来误差。一般情况下,在检测前进行深度校准时,探头处于静态,此时耦合层厚度很小(小于0.1 mm),可以不考虑耦合层的影响;但在扫查时,由于检测面高低不平、扫查速度大小、耦合剂的种类及浓度等会导致耦合层厚度发生变化。 此外,声波在耦合层中的传输速度一般小于在工件中的传输速度,由于耦合层厚度的变大(相对校准时),即声波在耦合层中传输时间变长,从而导致测量深度值增大。 为简便起见,假定已经对仪器用直通波进行深度校准,且认为在校准时耦合层厚度很薄,对声波的传输时间影响可以忽略。基于此,下面主要研究校准后的耦合层厚度变化对深度测量造成的影响。 (22) 其中,cc和cm分别为声波在耦合剂和工件中的传输速度。如果cc< L≈2H[1+0.5(cc/cm)2s2/(s2+d2)] (23) 对于极端情况下,即θ=90°时,此时d=0,声波在耦合层中的声程为最大,则式(23)可简化为: L≈2H[1+0.5(cc/cm)2] (24) (a)检测布置 (b)声束通过耦合层 通常使用的耦合剂为甘油、机油、化学浆糊或水,一般其声速为1 500 m/s,其中声速最大的为甘油,其声速为1 880 m/s[9],而工件的声速为5 950 m/s,这样cc/cm≈0.3,代入式(24),L≈2H[1+0.5(cc/cm)2]=2.09H,因此可取L≈2H。 这样可得到由于耦合层的变化,造成了时间测量误差:δt=L/cc,即: δt≈2H/cc (25) 将上式代入式(4),可得到深度d处的测量误差: (26) 通过试验,可以验证上式的正确性。 设PCS=100 mm,耦合剂为机油(声速cc≈1 400 m/s),试块声速cm=5 900 m/s,对仪器进行直通波深度校准后,调整耦合层厚度H=0.86 mm,试验数据见表4。 表4 耦合层厚度为0.86 mm时的深度测量误差 mm 通过上面试验数据可以看出,耦合层厚度的变化对深度测量有着很大的影响,特别是对靠近检测面缺陷深度测量的影响更大。 由于耦合层厚度的变化对深度测量有比较大的影响,所以在对检测图像进行分析时,仪器应具有(也应该有)二次校准功能。也就是说,在测量缺陷尺寸时,特别是测量缺陷深度时,可以再次利用直通波或底波对扫查图像进行深度校准,这样深度测量误差会大大减小。 比如使用直通波进行二次校准,由于耦合层的变化,深度d处传输时间为: (27) 直通波的传输时间为: tl=2H/cc+2s/cm+t0 (28) 因此这两个信号的声程差: (29) 对上式t和s求微分,仍可得到公式(16),从而消除耦合层厚度的变化对深度测量的的影响。 通常耦合层厚度是不均匀的,此时一般TOFD仪器或专用软件有两种方法解决:一是拉直直通波,即对不同位置的直通波进行二次校准;二是在不同缺陷测量点附近进行局部直通波校准(如果仪器没有直通波拉直功能),也同样达到精确测量的目的。 检测时,如果工件表面一侧有凸起(凸起高度为h),另外,工件焊缝两边存在错位或者厚度不等时造成检测面不平齐,都会带来深度的测量误差。 当检测面平齐时,深度d的衍射点的信号声程: 当检测面有一侧有凸起时,深度d的衍射点的信号声程: 则信号传输时间的变化量为: (30) 考虑到一般情况下h< (31) 将上式代入式(4),可得: δd=h/2 (32) 这样,因工件不平齐产生1 mm高度的变化,在深度测量时会有0.5 mm的误差。但是,如果测量的是缺陷高度而不是深度,那么该误差就会抵消。 当被检工件中的声速与预设的声速有偏差时,或者校准用试块的声速和检测工件的声速不同时,也会造成深度测量误差。 根据缺陷深度d的声波传输时间计算公式(1),可得: (33) 将式(33)代入式(4),进而得到: δd=-(s2+d2)δc/dc (34) 从式(34)可以看出,当被检工件声速比仪器预设的声速大时,即声波在工件中传输时间减小,显然测得的深度就会变浅。 例如,对于厚度50 mm的焊缝试件,PCS设为100 mm,仪器设置声速c=5.90 mm/μs,试求当工件实际声速为5.95 mm/μs时,深度10,20,40 mm的误差δd分别为-2.2,-1.2,-0.9 mm。 如已用直通波对仪器深度进行校准过,则此时声速变化引起的深度测量误差推导如下。 (35) 对于上面同样的例子,此时按式(35)则可得到深度10,20,40 mm的测量误差分别为-0.04,-0.09,-0.19 mm。 模拟信号数字化有着很重要的意义。由于模拟信号存在很多局限性:信号容易失真、测量精度低、抗干扰能力差、无法实现大规模存储、无法进行复杂的分析处理;而将模拟信号转换成数字信号则可以解决这些局限。 模拟信号数字化就是对模拟信号进行采样处理,即用相同的采样间隔(时间间隔)来测量模拟信号的瞬时状态参数,将一个时间连续的模拟信号转换成一个离散时间函数的信号样本。 模拟信号数字化处理带来的时间传输误差属于绝对误差范畴。图5示出数字化频率是信号频率的2倍时的情形,也就是说每个周期进行2次采样。这样的采样频率刚刚能够保证重建的数字波形频率不失真,却不能保证波形和波幅不失真。重建后的A扫波形与模拟信号存在较大不相似度:数字信号与模拟信号峰值点位置存在偏差Δ1,数字信号与模拟信号和横轴的交点存在偏差Δ2,因此在仅满足奈奎斯特极限的数字化采样频率(采样频率是信号频率的2倍)所采集的数据重建的A扫图形上测量,即使测量位置选择是正确的,也不能完全得到准确的信号到达时间。由此可见,数字化频率的高低会影响信号测量精度。 图5 数字采样频率对测量精度的影响曲线 NB/T 47013.10—2015[10]规定TOFD信号的数字化频率至少应是信号频率的6倍,即每个信号周期要采集6个样本,可以使峰值信号的平均误差在10%以内。 这样当选择交叉点或者样本顶点附近进行尺寸测量时,就会因采样的离散时间间隔造成时间测量误差,但时间误差不会大于采样宽度的一半[4]。 因此利用式(4)计算时,δt一般取数字化采样间隔的一半,δt的大小与数字化频率有关。又由于数字化频率一般取探头频率的6倍,也可以说δt与探头频率有关。可以通过提高数字化频率或探头频率来减小深度误差。 例如,对于厚度45 mm的工件,其纵波声速c=5.95 mm/μs,TOFD检测时,PCS设为100 mm,探头标称频率为5 MHz,假设数字化频率为探头频率的6倍,时间误差取数字化采样间隔的一半,则深度d为1,5,10,20,40 mm时的深度测量误差δd分别为2.0,0.4,0.2,0.1,0.07 mm。 由上例可以看出,TOFD技术在近检测面深度测量误差较大。 由模拟信号数字化处理带来的深度测量误差是无法消除的,提高数字化频率可以适当减小测量误差,但数字化频率太高也会造成其他问题,如会增大数据存储量、扫查时会使检测速度降低等。当然这里计算时取δt为采样宽度的一半是考虑偏差最大的情况,当测量点接近采样点时,误差就会大大降低。另外,对于远离检测面的深度区域,即使考虑偏差最大情况,其带来的深度测量误差也很小。 对于检测面有一定曲率,例如针对锅炉或压力容器筒体纵缝检测时,无论在筒体外壁(凸面)还是在筒体内壁(凹面),都会对缺陷的深度测量带来影响。 在筒体外壁或凸面进行检测时的探头布置如图6所示。缺陷实际距外壁深度为d,由于曲率的影响,仪器显示深度为d-δd,此时: (36) 式中R——工件外半径。 式(36)即为凸面检测时的深度测量误差。 图6 凸面检测探头布置示意 在筒体内壁或凹面进行检测时的探头布置如图7所示,此时应预先采用平板试块进行深度校准。假设缺陷实际距内壁深度为d,由于曲率的影响,仪器显示深度为d+δd,此时: (37) 式中r——工件内半径。 式(37)即为凹面检测时的深度测量误差。 图7 凹面检测探头布置示意 在对内壁检测数据进行离线分析时,除非所用仪器带有专用深度校准软件,一般不宜对图像进行二次深度校准。 轴偏移、PCS耦合层厚度变化、检测面不平齐、被检工件声速变化、模拟信号数字化处理、检测面曲率等是引起深度测量误差的主要因素;除此以外,还有一些次要因素也会对深度测量误差产生影响。 (1)楔块的磨损造成其厚度和角度的变化。 对于楔块的磨损造成其厚度变化使得声波在楔块中传输时间减小,可导致整个B扫查图像上移,因此深度测量会带来误差(深度值减小),此时需要进行二次校准才能消除或减小由于楔块磨损带来的影响;对于楔块磨损造成角度的变化,会影响预定的检测深度范围及该范围内的不同深度检测灵敏度。 (2)声束入射点的偏移。 在前面进行深度或深度误差计算时,均假定声波是从楔块的某个固定点进入工件的,但事实并非如此,从图8可以看出,声束入射点在声束覆盖的范围内是有偏移的。由于声束在楔块中有扩散,所以在工件中声束的上下边缘与主声束在检测面的入射点是有差异的。也就是说,工件中不同深度的声束由于其在检测面入射点的不同,造成PCS随深度变化。尽管如此,声束入射点的偏移对深度测量的影响还是很小的。 例如,使用钢中折射角为60°的楔块,探头标称频率5 MHz,楔块中声速2.4 mm/μs,工件中声速5.95 mm/μs,则楔块中的主声束角为20.44°,楔-12 dB声束扩散角为3.21°,上、下边缘声束角为 23.65°和17.23°。假定楔块中声程为8 mm,则分别可计算出图8中x1=2.3 mm,x2=2.8 mm,x3=3.3 mm。可以看出,上下边缘声束与主声束的PCS相差1 mm(即s相差0.5 mm)。此时工件中上边缘声束角已接近90°,即可认为x3为直通波的入射点。 图8 声束入射点偏移示意 对于较薄工件(厚度小于50 mm)且用直通波进行校准的,入射点的偏移是有一定影响的,但对于较厚工件的分区检测时(除第一分区外),影响则较小。 对上例并考虑极端情况,即考虑上下边缘波束时,缺陷深度d的衍射点的信号传输时间: (38) 直通波的传输时间: tl=2sl/c+t0=2(s-0.5)/c+t0 (39) 因此这两个信号的声程差为: ct=c(td-tl) (40) 对上式t和s求微分,另外考虑到同时采用直通波进行深度校准,故δtl=0,此时有δt=δtd,这样可以得到: (41) 将上式代入式(4),可得: (42) 对于s=50 mm,考虑入射点偏移情况时,用上式计算深度d在10,20,40 mm处的深度误差分别为-0.05,-0.1,-0.17 mm。可以看出,入射点偏移对深度测量造成的偏差是比较小的。主要原因是楔块或耦合剂的声速比工件的纵波声速低得多,楔块内声程又很短,使得楔块内声束在入射点处-12 dB扩散左右偏移量很小,因此在深度校准后,其造成深度测量的误差几乎可以忽略不计。 (3)工件声速的局部变化造成的声束偏转。 在工件内部,材质不均匀会造成声速局部变化,另外母材与焊缝之间的声速也会有一定差异,也会造成该部位的声束发生偏转,从而影响声波的传播方向和深度测量误差。总体来说,此种情况造成的影响很小、也比较复杂,只有在特殊情况才予以考虑,这里不再讨论。 本文分别讨论了影响深度(或高度)测量误差的各种因素,而在实际检测中,往往多个因素共同起作用,但每种因素对深度测量的影响不一样,如轴偏移使得深度测量数值变大,PCS负偏差(变小)时又使得深度测量数值变小。所以不能把各种影响因素引起的误差进行简单相加。总体来说,除直通波校准外,深度测量误差在近检测面是比较大的,这也是TOFD技术的一个特点,再加上检测面盲区的问题,因此对焊接接头厚度较小(可认为≤20 mm)时,采用双面TOFD检测是比较合适的。 通过深度(或高度)测量误差的分析,对TOFD检测也有很大意义。 (1)因为影响PCS精度的主要因素是探头前沿,因此检测前应对探头前沿进行精确测定。 (2)以PCS为基础计算深度,可能会产生很大的误差,而采用直通波、底面反射波或人工反射体进行校准,深度计算的误差要小得多。用直通波校准,在直通波处误差为零,随着深度增加,误差缓慢增加;用底面反射波校准,在底面的误差为零,随着深度减小,误差也缓慢增加,在近检测面处误差最大;当同时使用直通波和底波进行深度校准,深度测量精度较为理想。另外,使用人工反射体进行深度校准,在近检测面的误差也很大。 (3)在实际检测工作中,对于被检工件厚度小于50 mm时,最好在工件母材上同时使用直通波和底波进行深度校准,一方面保证校准后的深度测量误差小;另一方面可同时对楔块延时和声速进行校准,因为声速会随工件材料的不同而有所差异,仪器预设的声速只针对某种材料或某种材料的热处理状态。对大厚度工件的厚度分区检测时,第一通道可以使用工件母材直通波进行深度校准,其他分区应利用对比试块适当深度的人工反射体进行深度校准,为避免试块与工件声速不同的影响,最好能对工件的声速(相对数值)进行测量。 (4)对于检测面不平或曲面的情况,应对测量数据进行修正。 (5)检测结果分析时,应尽可能对图像进行二次校准。 (6)对于X形坡口的焊接接头,特别是焊缝宽度较大时,应使用其他检测方法确定缺陷在焊缝宽度方向上的位置,以避免由于缺陷轴偏移而造成的深度偏差。3 轴偏移引起的深度测量误差

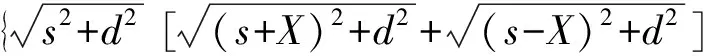

4 探头对间距(PCS)误差引起的深度测量误差
4.1 未进行深度校准时,探头对间距误差引起的深度测量误差
4.2 使用已知深度反射体回波校准后,探头对间距误差引起的深度测量误差


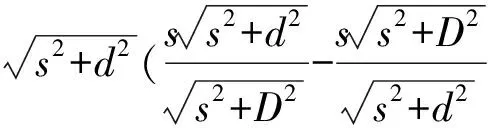



5 耦合层厚度变化引起的深度测量误差

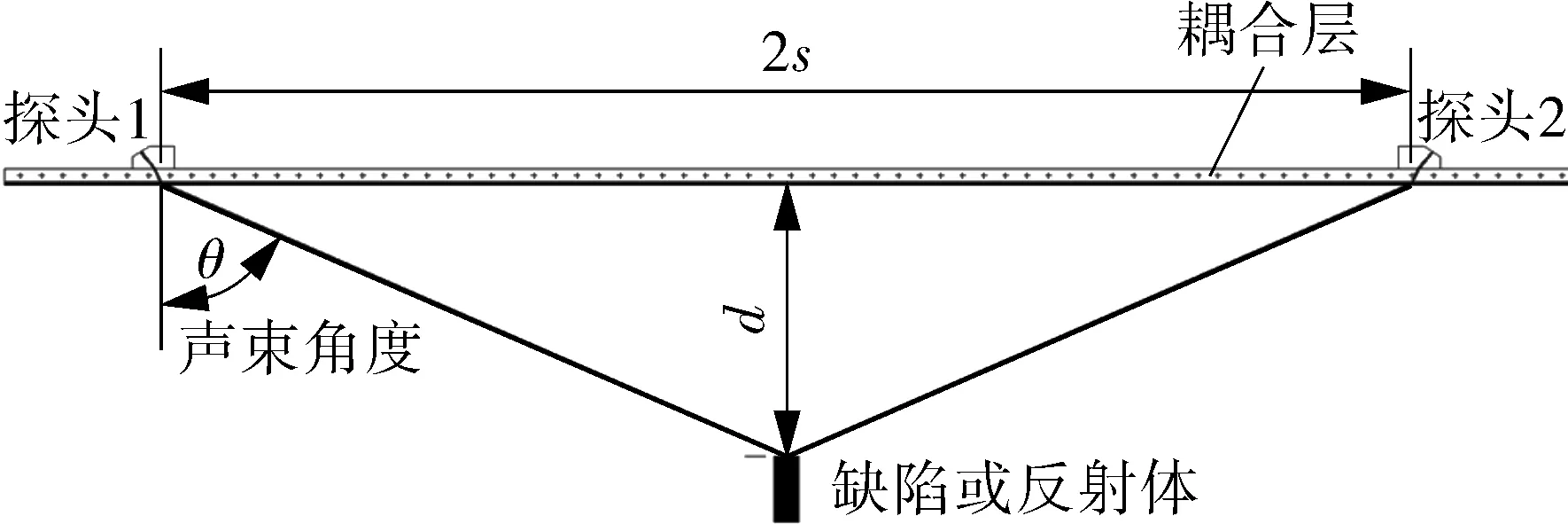
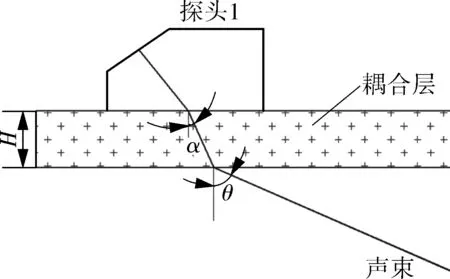

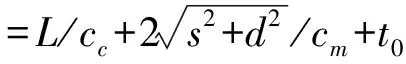
6 检测表面不平齐引起的深度测量误差
7 被检工件声速变化引起的深度测量误差
8 数字化处理引起的深度测量误差

9 检测面曲率引起的深度测量误差
9.1 凸面检测

9.2 凹面检测

10 影响TOFD技术深度和高度测量误差的其他因素

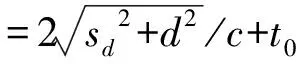
11 结语

