基于动态子结构法的加筋圆柱壳冲击环境预报

杨文山，杨 勇，赵 勋，郭 君，李晓文

（1.武汉第二船舶设计研究所，武汉 430064； 2.哈尔滨工程大学，哈尔滨 150001）

舰船冲击环境本质就是舰艇结构在水下爆炸载荷作用下位移、速度和加速度强弱的一种度量。二战过程中，由于忽视舰艇设备抗冲击能力预报，在水下爆炸载荷作用下，舰载设备系统大面积瘫痪导致美国海军损失近90艘舰艇，美军将部分毁伤舰艇结构进行改装，在太平洋海域进行大量实船水下爆炸试验累积大量实船试验经验及数据[2]。在20世纪70年代，前联邦德国海军也进行了大量实船水下爆炸试验试验，通过实验数据分析制定舰艇抗冲击标准BV043/1973[1]，随着武器爆炸技术发展，在上世纪80年代中期对原有标准进行升级改进提出新舰艇抗冲击标准BV043/1985。我国水下爆炸实船试验起步较晚，直至上世纪80年代针对028G开展实船水下爆炸试验，由于水下爆炸实船试验需投入大量人力、财力，我国目前冲击环境预报还是以数值有限元仿真方法为主，同时利用动力缩聚技术和模态综合技术提高了有限元计算的效率及精度。

对于动力缩聚技术，Guyan[3]和Iron[4]于1965年提出静态缩聚法，其主要是将结构整体自由度划分成主自由度和从自由度，并且忽略从自由度惯性力对结构模态信息的贡献，但是该方法缩聚仅能保证低频计算效果，高频误差极为明显，因而随后众多学者针对静态缩聚法不足提出众多改进方案。1989年O’Callahan[5]通过在缩聚过程中考虑惯性力影响提出IRS动力缩聚方法，该方法极大提高了高频计算精度，Friwell[6]提出的动力缩聚法，真正实现动力缩聚技术多步修正计算，针对IRS动力缩聚技术进行迭代，提出迭代IRS动力缩聚方法，瞿祖清[7]等提出的移频迭代技术可以是缩聚后结构动态特性在任意频段范围内逼近原始结构，魏震松[8]等通过简化迭代IRS动力缩聚技术，在计算收敛性和计算效率上均优于迭代IRS方法。要明伦[9]通过动力缩聚技术分析卧式新型海洋平台的动力特性，通过传统有限元数值仿真进行对比分析。

模态综合技术基本思路是将整体结构按照一定策略进行分解，分析分解得到的多个子结构系统动力学特性，将子结构按照原始界面几何连续原则进行装配连接，根据子结构间存在不独立坐标得到动力学方程，继而求解整体结构动力学特性。由于模态变换过程中，针对各个子结构仅选取少数模态进行综合，因而通过子结构方法降低整体结构求解阶数，既能提高计算效率同时还可以对更大更复杂的模型进行仿真计算。Hurty[10]于上世纪60年代首次提出固定界面模态综合技术，Craig和Bampton[11]提出Craig-Bampton方法对Hurry的固定界面模态综合技术进行改进，目前自由界面模态综合技术通常指Craig-Bampton方法。自由界面模态综合技术由Hou S.N.于1969年提出，综合过程中完全将高阶模态忽略导致计算精度难以保证，Rubin[12]在剩余柔度基础上引入剩余惯性项，提出2阶近似剩余模态综合方程极大提高了计算精度，王文亮[13]等采用李兹法给出自由界面模态综合方程。

在理论方面，Talyor[14]考虑流固耦合作用，给出平板结构在冲击波载荷作用下的响应方程。Huang[15]等研究了有限长弹塑性圆柱壳、简支圆板、固支方板、梁结构、无限长圆柱壳体、球壳在爆炸载荷作用下的动力学响应。在实验研究方面，Jin Qiankun、Ding Gangyi[16]通过非接触水下爆炸试验分析舱段子结构在远场非接触水下爆炸载荷作用下缩比模型冲击环境。

本文针对时域子结构自由界面模态综合技术综合过程中子结构求解方程进行推导，通过自由界面模态综合技术求解加筋圆柱壳结构在水下爆炸载荷作用下时域冲击响应并应用ABAQUS通用有限元软件对本文计算结构进行验证。

1 自由界面模态综合响应高效求解方法

1.1 子结构界面力求解

设有一结构可分解为若干个子结构，对任意子结构其动力控制方程可写为++Kx=F，子结构受到外力fa和界面力fb的作用

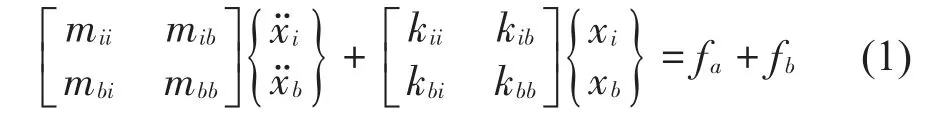
由于结构振动响应以低阶模态贡献为主，根据结构形式以及计算频率范围选择参与模态综合的保留模态，对结构矩阵进行降阶。设子结构模态为，其中分别是结构的低阶模态和高阶模态。

式(1)可变形为

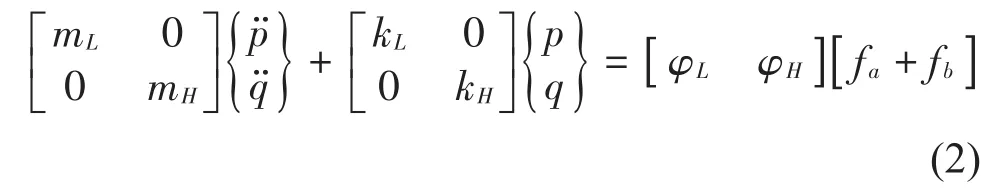
求解上述微分方程组可得到广义坐标响应

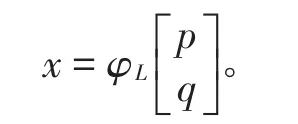
从数学上考虑，上式是2阶常微分方程组，针对有限元数值仿真的高阶数矩阵应用NewMark-β方法对自由界面模态综合方法求解结构动力响应进行推导，以加筋圆柱壳结构作为研究对象，从收敛性、计算步长、计算精度以及计算效率等方面对在冲击响应计算中应用进行分析。

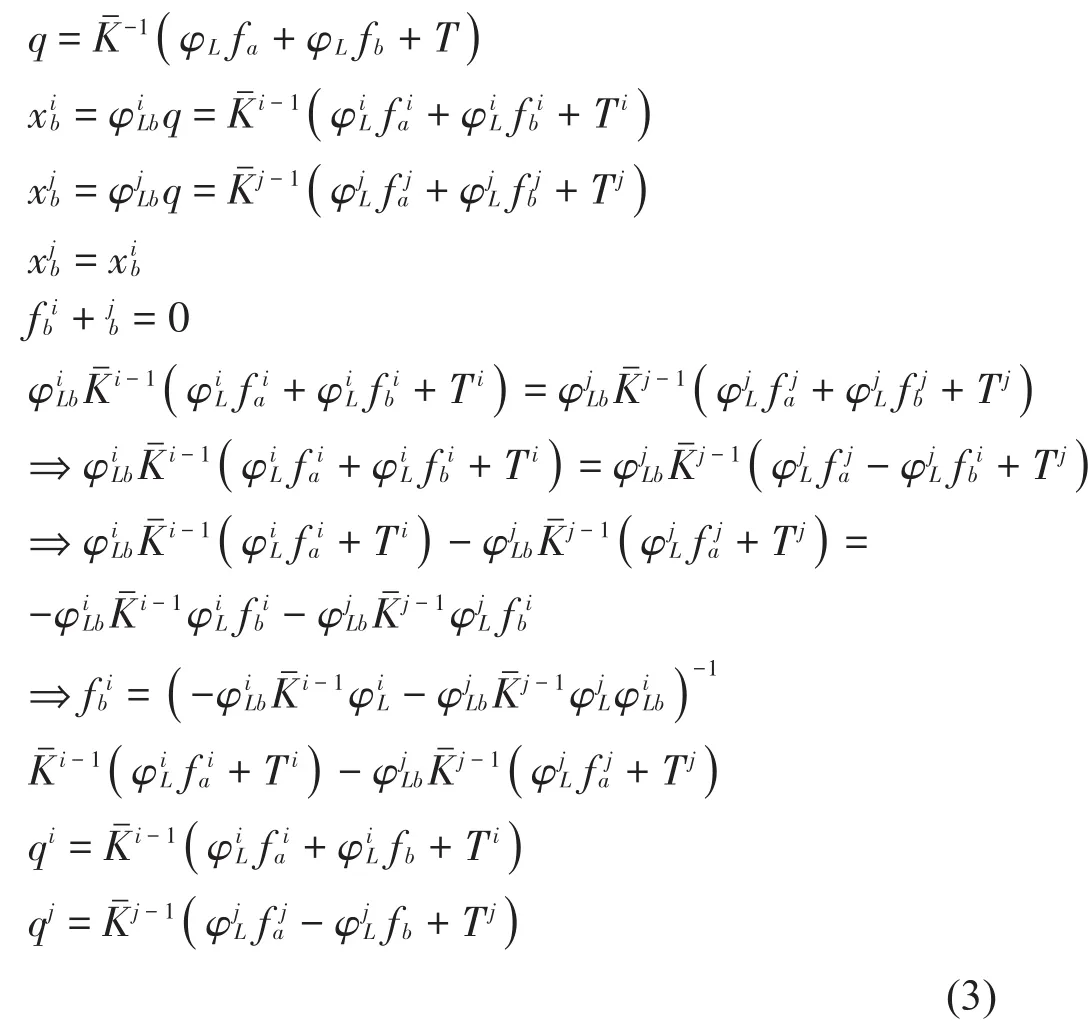
1.2 时域响应积分求解方法

Newmark法是一种逐步积分的方法，由于此方法为单独对每一个时间增量步的平衡进行求解，因此免除了任何方式的叠加应用，所以将此方法应用在对非线性动力学方程的求解中非常方便。Newmark法的计算推导过程如下：

以增量形式表达的运动控制方程为

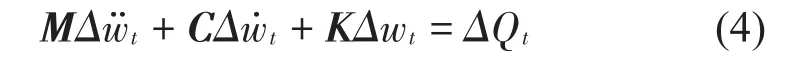
刚度阵

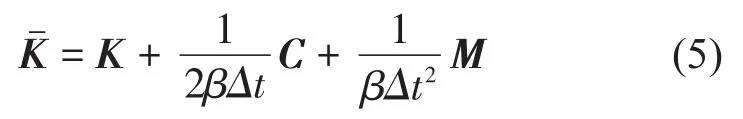
t+Δt时刻时的有效载荷为

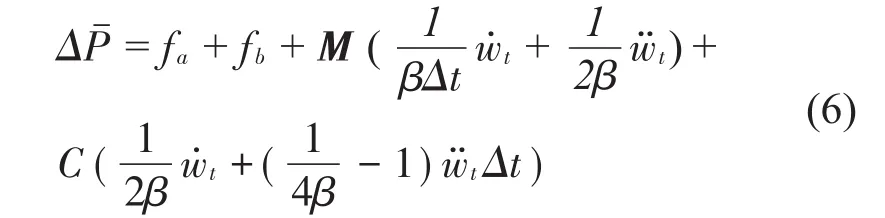
位移、速度与加速度的增量分别为

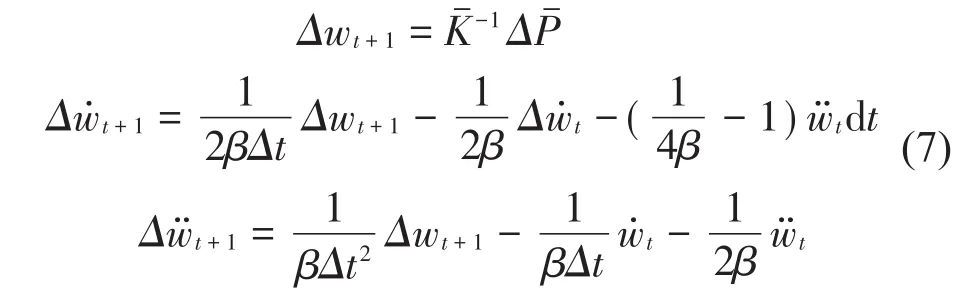
最终得到整体的响应为

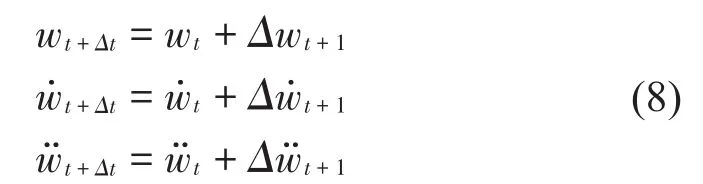
结合自由界面模态综合技术，界面力合力为0，界面位移相等原则

子结构动力响应为

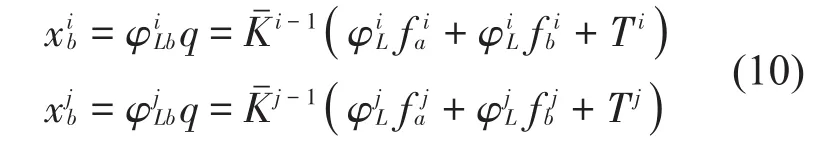
联立式（9）和式（10）可以求解界面力

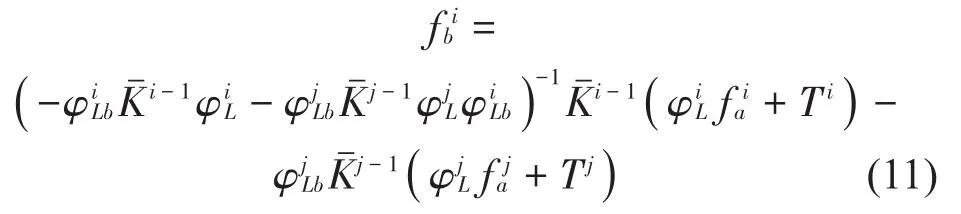
联立式（7）与 Newmarkq求解过程（11）可得Newmark方法界面力表达式

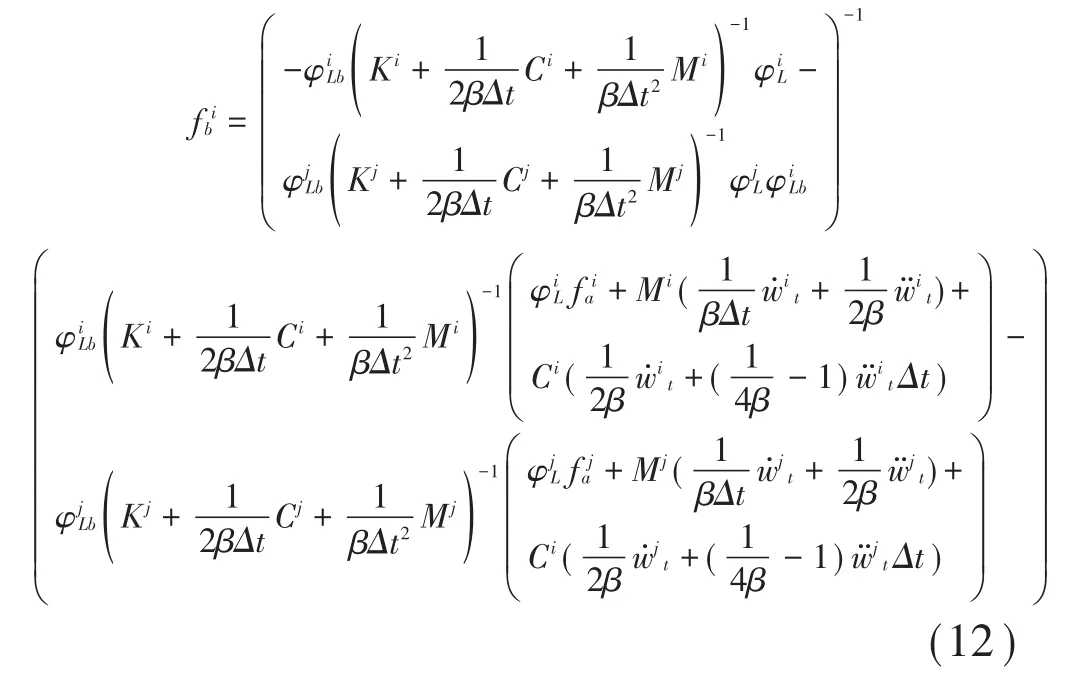
求解出界面力后,对于任意子结构受力情况完全已知，对任意子结构应用Newmark方法均可求解出任意时刻结构响应。

2 加筋圆柱壳自由界面模态综合响应

根据简化船体梁结构分析自由界面模态综合船体梁响应计算中应用，分析Newmark求解方法在自由界面模态综合中的应用及其计算积分理论计算效率、计算精度特点。水下爆炸冲击环境预报对象主要是水面舰船和潜艇，舰艇结构有限元仿真过程中通常会以板壳、梁结构进行简化，本节以加筋圆柱壳结构作为验证模型，应用动态子结构法计算爆炸载荷作用下结构冲击响应。

2.1 自由界面验证模型

为简化模型，本节将潜艇结构简化成加筋圆柱壳结构分析结构动力响应，加筋圆柱壳结构模型参数为：20 m×3 m×1 m；强力构件为T型材，壳板厚度为28 mm，杨氏模量E=2.1×10 Pa，泊松比ν=0.3，质钢材密度为ρ=7850kg/m3。通过ANSYS软件进行前期子结构建模和获取结构质量阵和刚度阵，结构模型如图1所示。

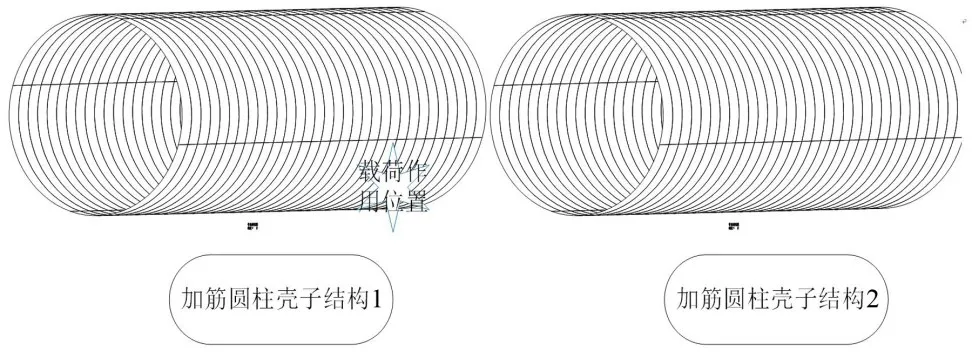
图1 加筋圆柱壳自由界面模态综合冲击环境预报模型

水下加筋圆柱壳子结构经过有限元离散后，得到共计得到1 120个三维板壳单元和1 120个梁单元，节点自由度数目6 816，选取60%自由度作为主自由度，其中包括全部界面自由度，剩余节点定义为从自由度，具体节点数界面自由度参数信息如表1所示。

应用自由界面模态综合方法计算加筋圆柱壳结构在冲击波载荷作用下结构时域响应信号。加筋圆柱壳结构如上文所述，将结构简化成船体梁，主要针对冲击波载荷进行简化，本节将冲击波载荷以节点集中力形式简化至梁结构各个节点位置处。圆柱壳简化成船体梁时：梁的各站剖面惯性矩、剖面积、剪切面积与圆柱壳对应相等，一个站距内剖面惯性矩、剖面积、剪切面积均分别相等，且将各站距内的质量均布于船体梁上。当爆源置于如图所示船中位置处时，分析舰船细长体结构，忽略冲击波载荷横向分量。对于沿船长方向纵向分量，由于冲击波载荷作用，结构相当于处于拉伸状态，导致结构固有振动频率明显升高，纵向分量不可忽略。对于纵向和垂向冲击载荷分别简化成式(13)

其中：F为等效集中力，P为冲击波压力，A为水线面面积，垂向载荷和纵向载荷如式(14)

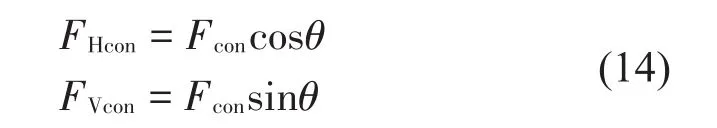
如图2所示，根据经验公式计算水下爆炸载荷压力曲线如图3所示

计算过程中，在同一站内认为其均匀分布，由于本次计算攻角设为90°，水下爆炸载荷在结构上投影面积即等效成水线面面积，图中压力幅值按式（14）在垂向和纵向分别进行分解，同一站内压力等效成节点集中力加载至各个节点，各剖面内均布载荷按式（14）等效至节点时的集中力为广义力，保证结构载荷等效的一致性。

其中经过分解后水下爆炸载荷垂向分量和纵向分量分布如图4所示。

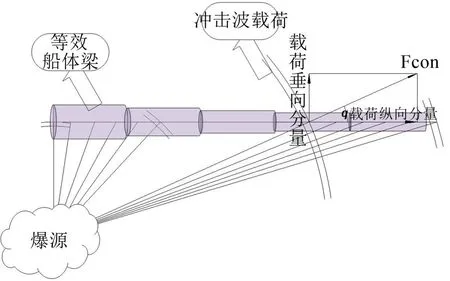
图2 等效船体梁载荷简化示意图

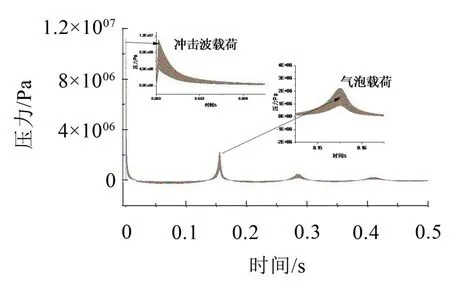
图3 水下爆炸载荷幅值曲线

计算压力载荷关于船体梁中横剖面对称，因而图4中仅节选船体梁船舯至船艏部分载荷，当节点与船舯距离超过20 m时，载荷纵向分量已经超过垂向分量，结合上文提到纵向载荷导致船体梁固有振动特性变化，因而结算过程中必须将载荷纵向分量考虑在内。

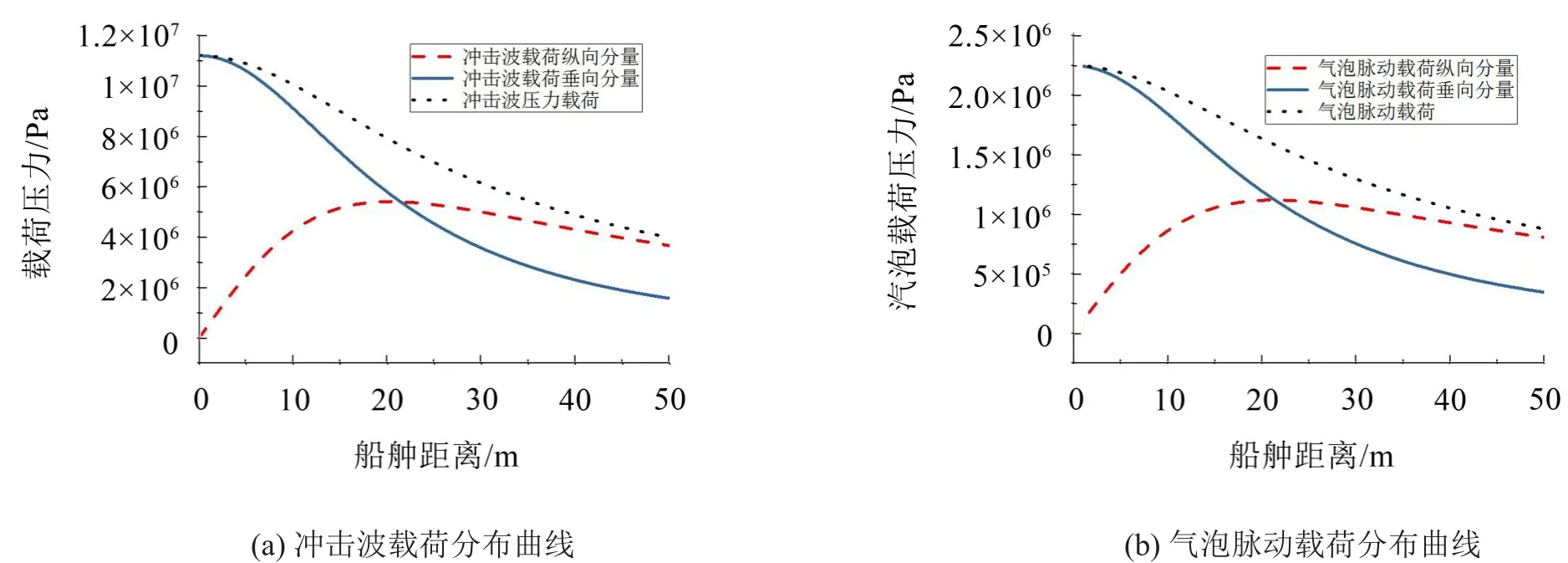
图4 水下爆炸载荷船体梁纵向分布曲线

2.2 加筋圆柱壳自由界面模态综合响应计算

如图5示，选取如图位置两组测点，使用Newmark方法计算加筋圆柱壳结构响应。

图5 加筋圆柱壳求解测点布置图

表1 模型节点数和传递矩阵维数

应用整体模型求解耗时657.8 s，双舱段子结构模型求解耗时323.9 s，计算效率提升50.76%。如图6所示应用自由界面模态综合技术求解加筋圆柱壳结构冲击环境预报，根据上文载荷简化方法具有可行性，就图6冲击谱谱线以及表2可以反映出对于10 Hz以上谱线匹配较好，反映至设计谱谱值，相较于谱速度和谱加速度预报结果计算误差低于10%，加载过程中，所有节点加载时间一致，接近于平面波加载，使得本文自由界面模态综合技术求解低频响应明显高于ABAQUS球面波加载方法。

由于载荷简化引起冲击环境预报差异主要集中于低频区间，因此会对低频谱位移冲击环境预报产生影响。

3 结语

（1）通过模态综合技术可以在不求解整体模态的基础上，仅通过界面位移方程和界面力方程等界面信息交换即可以较高求解效率并行计算各个子结构时域响应信号，对自由界面模态综合响应求解这一过程中涉及到的子结构界面力求解、动力方程组求解等问题进行说明。

（2）以简易加筋圆柱壳结构为模型进行冲击响应求解计算，自由界面模态综合求解加筋圆柱壳响应过程中，对冲击波球面载荷简化成节点集中力，该简化过程引起误差主要集中于低频区间，计算谱速度和谱加速度误差均低于10%，通过模态综合降低整体矩阵求解维度实现求解效率上提升，响应求解耗时降低50.76%。

表2 自由界面模态综合有限元仿真冲击谱值对比表

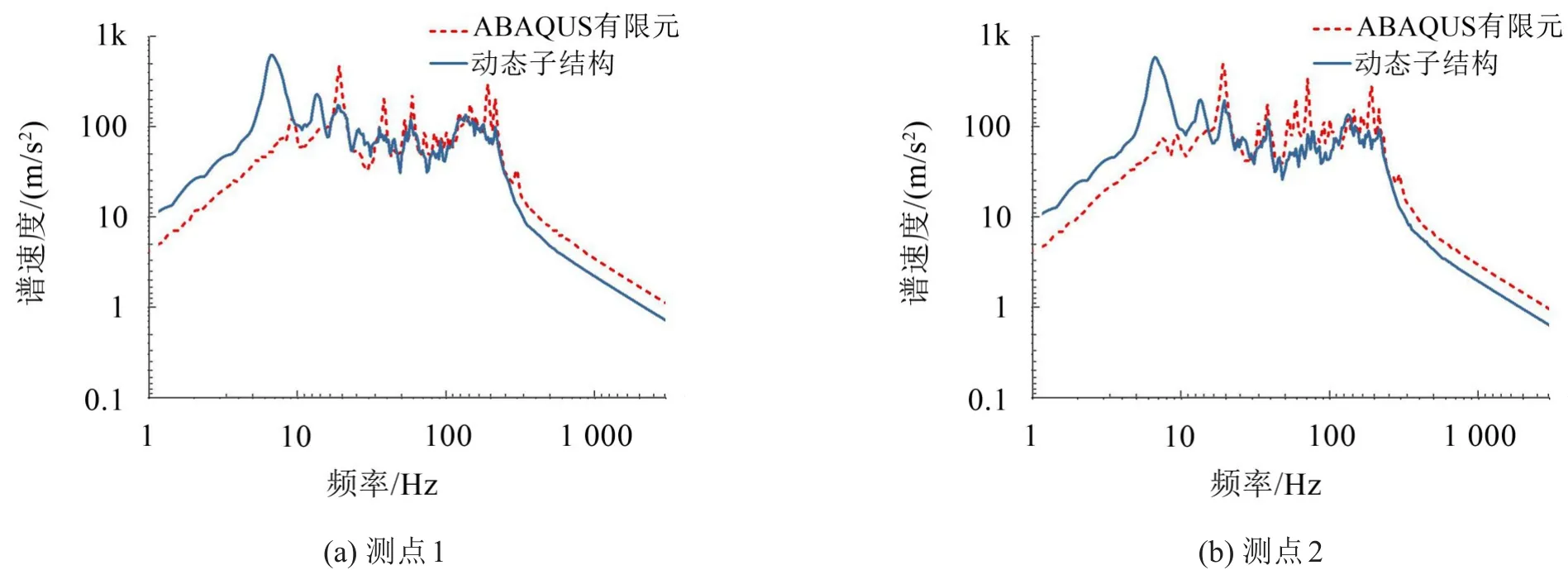
图6 自由界面模态综合求解加筋圆柱壳冲击谱曲线