基于CFD模拟的浓缩风能装置结构优化设计

姬忠涛，田 德

基于CFD模拟的浓缩风能装置结构优化设计

姬忠涛1，田 德2

（1. 曲靖师范学院物理与电子工程学院，曲靖 655011；2. 新能源电力系统国家重点实验室（华北电力大学），北京 102206）

浓缩风能装置的结构直接影响浓缩风能型风电机组的性能。在该文中，采用计算流体力学软件对浓缩风能装置进行结构优化。优化方案是在原模型扩散管后增加一段锥形管，并分析锥形管的母线长度及偏转角对浓缩性能的影响。分析结果表明，锥形管母线长度为0.4（为中央圆筒直径），偏转角为50°时的优化模型为较优模型。浓缩风能装置优化模型的浓缩性能由锥形管后方的漩涡和锥形管内壁面上的流动分离决定。漩涡的存在使浓缩风能装置优化模型的浓缩性能优于原模型。流动分离会使浓缩性能降低。使浓缩风能装置得到优化的最佳状态是锥形管后方出现一个强烈的漩涡，同时锥形管内壁面附近不出现强度较大的流动分离。

风能；计算流体力学；优化；浓缩风能装置；漩涡；流动分离

0 引 言

众所周知，风电机组的功率与风轮处风速的三次方成正比[1-3]。这意味着，即使风速上很小的提升，都会使风电机组的功率大幅度增加[4]。因此，科研人员对传统风电机组进行优化设计[5]，以尽可能多地提取风中蕴含的能量[6]，其中最可靠的方法是采用浓缩风能型风电机组[7]。

浓缩风能装置作为浓缩风能型风电机组的核心部件，由收缩管、中央圆筒和扩散管组成[8-10]。由于空气自中央圆筒流出后，在扩散管内部会出现流动分离，因此扩散管的结构对浓缩风能装置的浓缩性能影响最大[11]。

在扩散管的结构优化方面，Coşoiu等[12]通过在扩散管上开4个环形槽的方法连接浓缩风能装置外壁高压区和内壁的流动分离区，使流动分离区向扩散管出口方向推移，进而使浓缩风能装置性能得到大幅提升。Ohya等[13]采用在扩散管出口处增加法兰盘的方法对浓缩风能装置进行结构优化，使风电机组的输出功率提高了4～5倍。Kardous等[14]对安装有法兰盘的浓缩风能装置利用仿真和可视化系统观察的方式进行了研究，发现法兰盘的高度对浓缩风能装置性能影响较大；且随着法兰盘高度的升高，其对浓缩风能装置性能的促进作用会减弱。

对于安装有法兰盘的浓缩风能装置，其浓缩性能较好，但其轴向长度较大，用在高处不易控制；且法兰盘为回转体，其母线与轴线垂直。母线与轴线夹角小于90°，即将法兰盘替换为锥形管的情况并未加以讨论。

因此，在本论文中将通过在浓缩风能装置扩散管外缘增加一段锥形管的方法对浓缩风能装置进行优化，并采用计算流体力学软件对优化模型进行分析，得出浓缩风能装置最优模型，并分析结构优化对浓缩风能装置浓缩性能的影响机理。

1 结构优化方案

结构优化对象为100 W浓缩风能型风电机组所用的浓缩风能装置。图1所示为浓缩风能装置结构优化示意图。其中，收缩管母线、中央圆筒母线、扩散管母线绕回转轴旋转一周形成一个回转面，然后通过加厚5 mm即可形成浓缩风能装置原模型。收缩管母线左端点绕回转轴旋转一周形成入口圆。其中，为扩散角，浓缩风能装置模型中央圆筒内径为，其值为900 mm。为提升浓缩风能装置的浓缩性能，在浓缩风能装置扩散管外缘新增一段锥形管。该锥形管母线为EF，长度为，与竖直方向的夹角，即偏转角，为。优化方案如下：将的值定为0.1、0.2、0.3、0.4、0.5、0.6，每个值对应的为0°、10°、20°、30°、40°、50°、60°，并对值为0，即原模型进行一次模拟计算，以确定最佳的优化模型。计算次数总计为43次。

中间截面位于中央圆筒中部，风轮即安装在中间截面上，因此中间截面处的风速将直接影响浓缩风能型风电机组的功率输出。为评价浓缩风能装置优化模型的性能，在中间截面上沿45°方向均匀布置21个点，其中最下面一点在轴线上，最上面一点是个例外，因为该点设置在中央圆筒内壁面上的话，在计算流体力学软件中将无法取点，因此该点设置在距离中央圆筒内壁面2 mm处。其他20个点中，相邻2个点之间的间距为22.5 mm。同时，中央圆筒出口平面与轴线交于一点，过该点沿90°方向均匀布置21个点，布置方法及间距与中间截面上21个点类似，区别在于位置和方向。

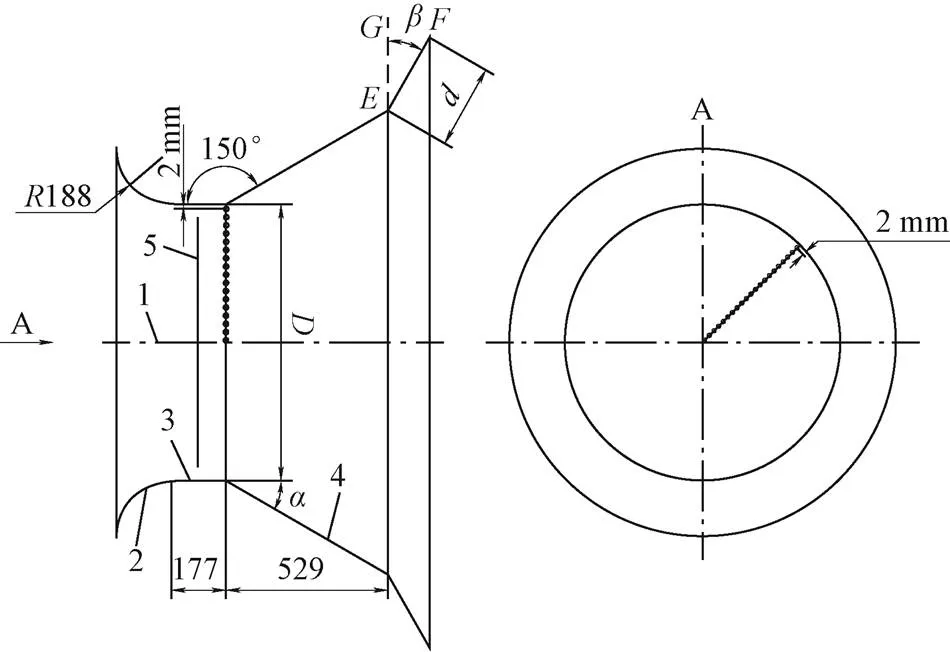
1.回转轴 2.收缩管母线 3.中央圆筒母线 4.扩散管母线 5.中间截面

1.Rotation axis 2.Generatrix of shrinkage pipe 3.Generatrix of central cylinder 4.Generatrix of diffuser 5.Middle section

注：为收缩管母线半径，mm；表示竖直方向；为锥形管母线长度，mm；为偏转角，(°)；为中央圆筒直径，mm；为扩散角，(°)。

Note:is the radius of generatrix of shrinkage pipe, mm;indicates vertical direction;is generatrix length, mm;is deflection angle, (°);is the diameter of central cylinder, mm;is diffusion angle, (°).

图1 浓缩风能装置结构优化示意图

Fig.1 Sketch diagram of structural optimization design of concentrator

2 计算流体力学分析

2.1 建立模型

根据图1所示浓缩风能装置各项尺寸，通过CAD软件建立浓缩风能装置优化模型。图2a是为0.2，为20°时的浓缩风能装置优化模型。将其导入到有限元分析软件中，创建一个直径为20 m，长度为30 m的圆柱。该圆柱与浓缩风能装置优化模型共用同一个对称轴，且该圆柱顶圆圆心与浓缩风能装置优化模型入口圆圆心间距为5 m，底圆圆心与浓缩风能装置优化模型入口圆圆心间距为25 m。通过布尔减运算在圆柱中减去浓缩风能装置优化模型，最终即可得到流体场模型如图2b所示。

图2中的浓缩风能装置内部未设置风轮，将浓缩风能装置中央圆筒内部视为一个风场。对浓缩风能装置进行结构优化的目的是在外部气流条件相同的情况下，使该风场蕴含的风能尽可能多，在此过程中无需考虑风轮的阻挡作用。通过结构优化对浓缩风能装置定型之后，再对风轮进行优化，以尽可能多地从该风场中获取风能。

2.2 网格划分

对流体场划分网格时，采用patch conforming算法，网格类型为四面体网格，相关中心（relevance center）选细化（fine），相关性（relevance）设为70。在浓缩风能装置表面附近划分出膨胀层；划分方法是在浓缩风能装置表面1cm的厚度范围内划分出20层的膨胀层。膨胀算法（inflation algorithm）为Post。划分好的网格如图2c所示。

图2 计算流体力学分析前处理结果

2.3 参数设置

在本文中，每一次计算流体力学分析，除了浓缩风能装置结构上的不同以外，其他设置均相同。

2.3.1 湍流模型

在本文中，湍流模型为SST-模型，即剪切应力输运-模型。这种模型将-模型和-模型结合起来运用；其在壁面附近采用-模型，在边界层外部采用-模型，这样既可以使计算结果更加准确，又可以降低计算成本。该模型考虑了湍流剪切应力的传递，可以对不同压力梯度下流动分离的开始及尺度进行高度准确地预测[15-17]。众多科研人员，如Heikal[18]、Kosasih[19]、Wong[20]等，采用SST-模型进行浓缩风能装置相关研究，并将计算结果与试验结果进行比较，结果表明，采用SST-模型对浓缩风能型风电机组的性能进行预测是可靠的。

2.3.2 数值仿真计算条件

仿真计算时，考虑热交换，启用能量方程。流体介质是空气。在对由相同收缩管、中央圆筒和扩散管制成的浓缩风能装置进行车载试验时，当风速为10.83 m/s时，安装在浓缩风能装置内部的风轮达到发电机的额定转速，因此将风速定为10.83 m/s[21]。同时，在进行车载试验时，环境温度为296.75 K，大气压强为88 800 Pa，因此在数值仿真时温度及压强依此2参数进行设置。同时通过查表的方式查得密度、黏度、导热系数、恒压比热容分别为1.044 kg/m3、1.85×10-5kg/(m·s)、0.026 22 W/(m·K)、1 013 J/(kg·K)。根据浓缩风能装置的尺寸进行计算，得出流量、湍动能、比耗散率分别为3 552.048 kg/s、0.165 382 m2/s2、11.786 s-1。浓缩风能装置表面的粗糙高度定为0.3 mm，离散格式为二阶迎风格式。

进口边界为质量流量入口，流速方向定为与进口边界垂直。浓缩风能装置壁面以及流体场外壳壁面的热边界条件均采用固定温度，其值为296.75 K。出口边界采用压力出口。

2.4 仿真计算验证

在文献[22]中，对比分析了对浓缩风能装置进行车载试验时得出的试验数据及仿真数据。分析结果表明，中央圆筒中间截面处仿真计算值与实际测量值的相对误差在5%和10%以内的点所占百分比分别为41.67%和83.33%，即多数误差在10%以内，基本满足定量预测要求。在对比不同浓缩风能装置浓缩性能时，仿真计算可以得出与车载试验相同的结果，因此文献[22]中的仿真计算方法可以用来对浓缩风能装置进行定性分析。在本论文中，采用的仿真计算方法与文献[22]中的仿真计算方法相同，因此仿真计算结果是可靠的。

3 结果与讨论

3.1 优化性能分析

中间截面的风速直接影响浓缩风能型风电机组的功率输出；同时中央圆筒出口截面上的静压越低，则浓缩风能装置浓缩性能越好。因此，在本节中，将比较中央圆筒出口截面上21个点的平均静压，以及中间截面上21个点的风速大小，进而得出最佳的值及值。

3.1.1 偏转角优化性能分析

图3为不同值及值时，中央圆筒出口平面上21点平均静压变化图。为了使每个值对应的不同偏转角的浓缩风能装置优化模型均可以和原模型进行比较，图中70°对应的点为原模型中央圆筒出口处21点平均静压。

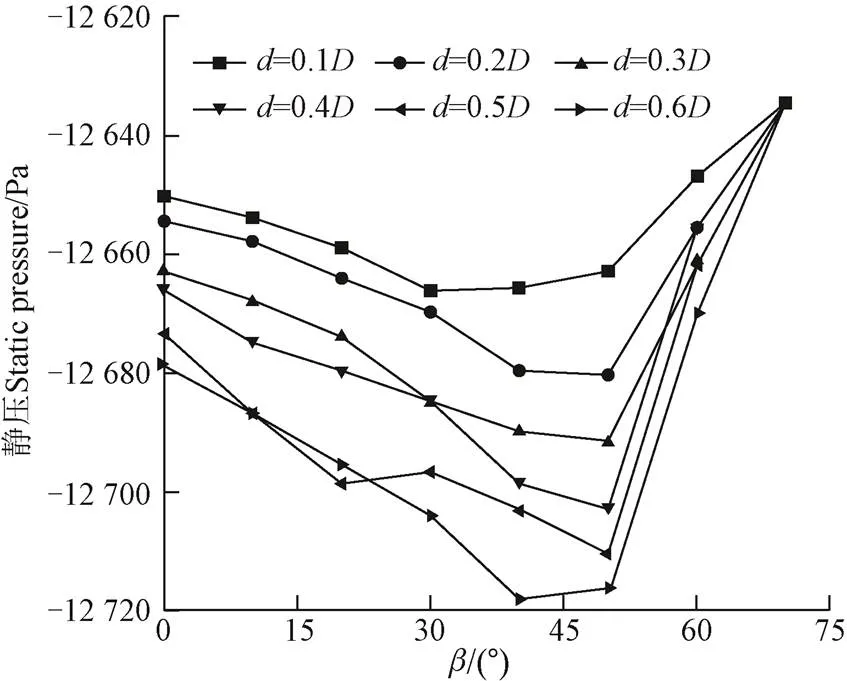
图3 不同母线长度及偏转角对应的中央圆筒出口处21点平均静压变化图

从图3中可以看出，所有优化模型的平均静压均低于原模型的平均静压，说明在原模型扩散管外缘新增一段锥形管起到了优化浓缩风能装置的作用。当为60°，值在0.1至0.6之间变化时，与为其他角度时相比，平均静压随值的增加降低不明显，甚至出现略微升高的情况。这说明简单地将原模型的扩散管延长对其浓缩性能的提升有限。当偏转角为0°，值在0.1至0.6之间变化时，平均静压随值的增大降低，但降低幅度不大。在偏转角位于10°至50°之间时，平均静压随值的增大基本上呈降低趋势，且随偏转角的升高，降低的幅度基本上逐渐加大。当值为0.1时，偏转角为30°时平均静压最低，且偏转角为30°、40°、50°时平均静压相差不大；当值为0.2、0.3、0.4和0.5时，偏转角为50°时平均静压最低；当值为0.6时，偏转角为40°时平均静压最低，且偏转角为40°、50°时平均静压相差不大；从中可以看出，值为0.1和0.6，偏转角为50°时，浓缩风能装置优化模型浓缩性能较好；而值为其他值时，浓缩性能最优，因此可以认为为50°时，浓缩风能装置优化模型的浓缩效果最好。

3.1.2 母线长度优化性能分析

风电机组的输出功率与风轮处风速的三次方成正比，若风轮处风速增加为原来的倍，则风电机组的输出功率将增加为原来的3倍。

令=0.1、0.2、0.3、0.4、0.5、0.6。设为50°，值为时，浓缩风能装置中间截面处的平均风速为V，可吸收风能为W，原模型中间截面处的平均风速为0，可吸收风能为0。将浓缩风能装置中间截面上21点处风速的平均值定为中间截面处的平均风速。

提取原模型以及为50°时不同值对应模型中间截面处的21点风速，并计算其平均值，得出原模型中间截面处的平均风速为15.3 m/s；为50°时，值分别0.1、0.2、0.3、0.4、0.5、0.6时对应浓缩风能装置模型中间截面处的平均风速分别为18.1、19.0、18.9、19.7、19.9、20.6 m/s，则V/0分别为1.185、1.240、1.234、1.285、1.301、1.342，W/0分别为1.664、1.906、1.882、2.124、2.202、2.419，其中W/0是V/0对应数据的三次方。

图4是W/0随值的变化图。从图中可以看出，W/0随值的增加总体上呈递增趋势。当0.1≤≤0.2时，W/0随值增长较快；当0.2≤≤0.3时，W/0随值的增长有所减小，但减小幅度不大；当0.3≤≤0.4时，W/0随值的增长大幅提高；当0.4≤≤0.5时，虽然W/0在增长，但增长量较少；当0.5≤≤0.6时，W/0随值增长较快，但增长幅度小于0.3≤≤0.4时W/0的增长幅度。考虑到随着锥形管母线长度延长，对应浓缩风能装置成本将大幅上升，因此将锥形管母线最佳长度定为0.4。

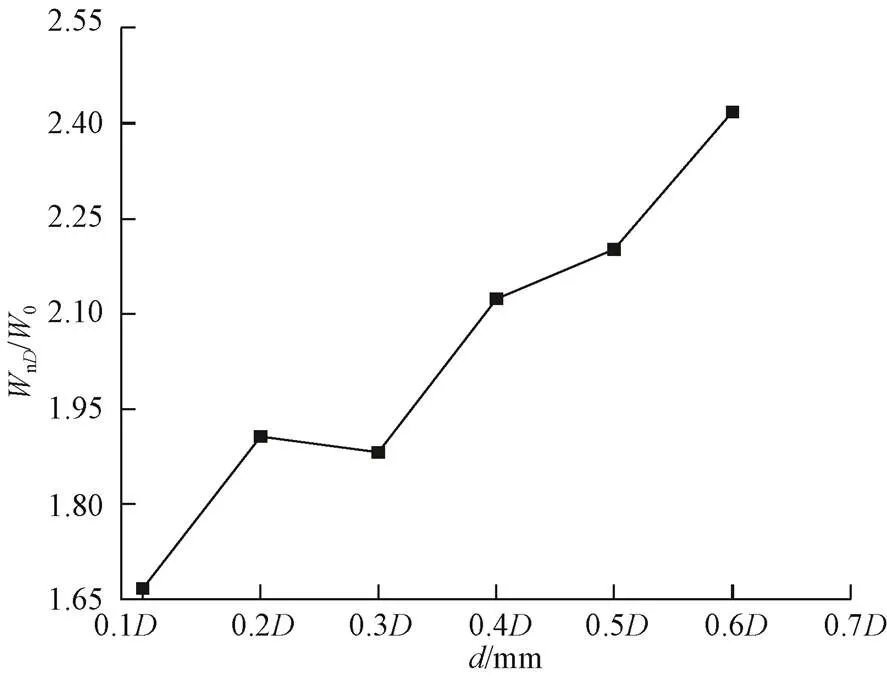
图4 可吸收风能增长率WnD /W0随d值变化图

3.2 优化机理分析

3.2.1 浓缩性能的影响因素

决定浓缩风能装置浓缩性能的关键因素是扩散管内壁上的流动分离。发生流动分离，浓缩风能装置的浓缩性能将变差。但流动分离之后，如果流线可以重新向扩散管内壁靠拢，则浓缩风能装置的浓缩性能将得到提高。

若使扩散管内壁不发生流动分离，要求图1中的扩散角在4°左右[23]；在这种情况下，如果要使浓缩风能装置的浓缩性能依然较好，则要求浓缩风能装置出口面积与入口面积之比保持为某一个值，那么就会导致浓缩风能装置轴向长度较长，会使浓缩风能装置成本升高，且可能使浓缩风能型风电机组的重心不在立柱轴线上，进而带来一些潜在的危险。

随着信息交流环境的迅速变化，强化服务已成为公共图书馆发展的迫切要求，而只有通过基于用户的研究，公共图书馆服务才能更加贴近用户需求，利用有限的资源产生最大的社会效益。

流动分离之所以能够导致浓缩风能装置浓缩性能变差，主要原因在于出现流动分离时，扩散管内壁面附近的气流会向远离扩散管内壁面的方向流动，进而导致扩散管轴线附近一段距离内的流速升高，而该距离之外的部分流速降低，甚至出现逆流现象，并最终导致通过扩散管横截面总的质量流量降低，进而使中央圆筒中间截面的流速降低，导致浓缩风能装置浓缩性能变差。

为便于分析，将值为，值分别为0°、10°、20°、30°、40°、50°、60°的模型分别编号为10-0、10-10、10-20、10-30、10-40、10-50、10-60号模型。如优化模型的值和值分别为0.4和50°，则优化模型为4-50号模型。

为分析优化模型的浓缩性能优于原模型的原因，图5给出了4-50号模型和原模型的剖面速度矢量图。从图中可以看出，锥形管后方产生了漩涡，而漩涡中的风速较高，对应静压较低，因此在锥形管后方形成了一个强烈的低压区，形成对浓缩风能装置优化模型内部强烈的抽吸作用，使空气加速向锥形管外缘流动，进而使中央圆筒出口处的流量提升，中央圆筒中间截面处的风速提高。

从图5可以看出，锥形管后方的漩涡是导致浓缩风能装置优化模型浓缩性能提升的关键因素，而不同优化模型的浓缩性能是有差别的，因此在后文中将通过将锥形管后方的速度矢量图放大后进行分析，以确定其原因。

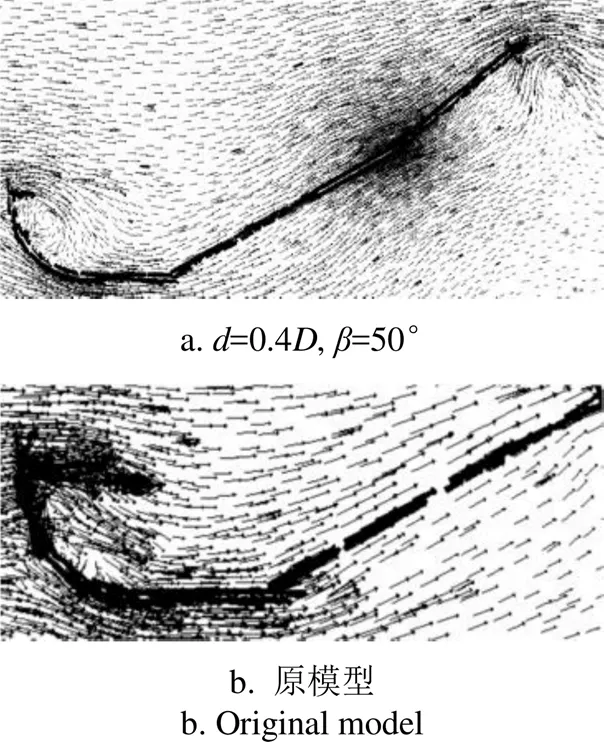
图5 优化模型（d=0.4D，β=50°）与原模型剖面速度矢量图

3.2.2 偏转角优化机理分析

优化模型的值和值分别为0.4和50°，因此为了研究偏转角的优化机理，本节对4-0、4-10、4-20、4-30、4-40、4-50、4-60号模型的计算结果进行分析。从图3中可以看出，当=0.4时，浓缩风能装置优化模型浓缩性能由高到低依次为4-50号模型、4-40号模型、4-30号模型、4-20号模型、4-10号模型、4-0号模型、4-60号模型。在计算流体力学软件中将7个模型对应锥形管后方的速度矢量图放大后如图6所示。

从图6a可以看出，4-0号模型由于偏转角为0°，因此相当于原模型扩散管外缘增加了一个法兰盘。法兰盘右边的壁面为内壁面。该法兰盘后方形成了漩涡；此漩涡中心的静压较低，使法兰盘外壁面边缘喷出的空气亦受到此漩涡中心的吸引进而向法兰盘内壁面方向运动。与漩涡中心距离稍远的地方由于风速较大，压差形成的向心力小于气流旋转产生的离心力，导致这些气流偏离漩涡中心而向法兰盘下方流去；法兰盘内壁下方存在相对较高的静压区，则向法兰盘内壁面下方流去的气流必须通过减速升压与逐渐升高的静压抗衡，并最终与原模型扩散管喷出的气流混合向下游流去。法兰盘外缘流出的空气由于漩涡的存在向原模型扩散管出口流动，进而阻碍原模型扩散管喷出的气流向上方扩散；此外，法兰盘内壁面下方出现了流动分离，使原模型扩散管出口处流出的气流向上方扩散不畅，这些均导致4-0号模型的浓缩性能下降。

从图6c可以看出，对于4-20号模型，与4-10号模型类似，锥形管内壁面下方发生的流动分离变弱，原模型扩散管出口喷出的气流向上方的扩散情况得到进一步改善，因此4-20号模型的浓缩性能得到进一步的提高。

从图6d可以看出，对于4-30号模型，产生的漩涡中心位置与锥形管内壁面之间的距离变大，锥形管外缘喷出的气流经漩涡中心吸引流向锥形管内壁面的量变得更少，锥形管内壁面下方发生流动分离的位置以及与原模型扩散管出口处喷出的气流混合向下游流去的位置均更加靠上，进而原模型扩散管出口喷出的气流可以更好地向上方扩散，进而导致4-30号模型的浓缩性能进一步提高。

从图6e可以看出，对于4-40号模型，漩涡中心与锥形管内壁面间距变得更大，导致原模型扩散管出口喷出的一部分气流被漩涡吸引由漩涡和锥形管内壁面之间流过，并与锥形管外缘喷出的气流混合向下游流去。另一部分气流流向漩涡并与漩涡上方流过的气流混合向下游流去。锥形管内壁面下方还存在较高的静压区，因此在该位置发生了流动分离，但强度不大。总体上看，4-40号模型扩散管出口喷出的气流可以较为顺畅地向上方扩散，因此4-40号模型与4-30号模型相比，其浓缩性能得到大幅提高。

从图6f可以看出，对于4-50号模型，漩涡强度较大，且其中心静压较低，与锥形管内壁面间距依然较大，进而导致原模型扩散管出口喷出的气流更多地向漩涡和锥形管之间流动。由于偏转角较大以及漩涡的存在，进而导致锥形管内壁面下方未出现流动分离。因此，与4-40号模型相比，扩散管出口喷出的气流向上方扩散更为顺畅，因此4-50号模型的浓缩性能得到进一步地提高。

从图6g可以看出，4-60号模型只是将原模型扩散管简单地延长，锥形管外缘喷出的气流速度会得到提高，进而对模型内部的抽吸作用会提高。虽然锥形管后方产生了漩涡，但漩涡强度不大，且距离锥形管内壁面较远，因此其浓缩性能的提升幅度是有限的。

由以上分析可知，浓缩风能装置优化模型的浓缩性能是由锥形管后方的漩涡和锥形管内壁面上的流动分离决定的。总体上看，锥形管后方出现的漩涡可以形成对浓缩风能装置优化模型内部强烈的抽吸作用，进而使浓缩性能提升。因此从图3中可以看出，所有优化模型的浓缩性能均优于原模型。锥形管偏转角越小，则漩涡强度越大，以至于可以将锥形管外缘喷出的气流向锥形管内壁面吸引，进而影响扩散管出口处的气流径向上的扩散，使原本优越的浓缩性能降低。同时，偏转角越小，锥形管内壁面上越容易出现流动分离，进而使浓缩性能降低。因此，最佳状态是锥形管后方出现一个强烈的漩涡，但该漩涡的强度不至于将锥形管外缘的气流过多地向锥形管内壁面吸引，同时锥形管内壁面附近不出现强度较大的流动分离。母线长度为0.4时，偏转角为50°，可以实现此状态。

图6 待选模型（d=0.4D）锥形管后方剖面速度矢量图

3.2.3 母线长度优化机理分析

为了研究母线长度的优化机理，本节对1-50、2-50、3-50、4-50、5-50、6-50号模型的计算结果进行分析。在计算流体力学软件中将6个模型对应锥形管后方的速度矢量图放大后如图7所示。

从图7a中可以看出，目前计算条件下，1-50号模型锥形管后方未发现旋涡，但在锥形管后方存在速度方向的剧烈改变，这种情况容易导致小范围内风速的升高，进而在锥形管后方形成了一个低压区，对浓缩风能装置优化模型内部形成了抽吸作用，使气流能够更好地沿径向扩散，且锥形管内壁面上并未出现流动分离，因此浓缩性能得到较大提升。

从图7b中可以看出，由于母线长度变大，2-50号模型锥形管出口处的速度进一步升高，锥形管后方也存在速度方向的剧烈改变，且接近于形成漩涡，因此在锥形管后方形成了一个低压区，对浓缩风能装置优化模型内部形成了更为强烈的抽吸作用，使浓缩性能得到了进一步提升。

由图7c可以看出，随着母线长度继续变大，3-50号模型锥形管后方出现了漩涡，但该漩涡的中心距离锥形管内壁面较远，以至于对扩散管出口喷出的气流沿径向上的抽吸作用不够强烈，且锥形管内壁面中部偏上位置出现了流动分离现象，这会导致中央圆筒内壁附近的几个点的速度降低幅度过大，进而使中间截面上21个点的平均速度稍低于2-50号模型。因此，与2-50号模型相比，虽然母线长度的变大使漩涡开始出现，但浓缩性能稍有下降。

从图7d可以看出，随着母线长度继续变大，4-50号模型锥形管后方的漩涡更加强烈，使距离锥形管内壁面较远距离的气流都被吸引从漩涡和锥形管内壁面之间流过，进而更好地促进了气流的径向扩散。虽然锥形管内壁面中部偏上位置出现了轻微的流动分离现象，但对浓缩性能的影响不大，因此浓缩性能得到了较大提升。

从图7e可以看出，5-50号模型锥形管后方出现了更为强烈的漩涡，对浓缩风能装置优化模型内部的抽吸作用更强，可以使浓缩性能得到大幅提升；但母线长度变大，导致锥形管内壁面附近出现了由锥形管入口至出口之间的逆压梯度，进而使锥形管内壁面中部出现了较强的流动分离，可以使锥形管内气流沿径向向上的扩散受到阻碍，进而使浓缩性能减弱，因此两相抵消，虽然5-50号模型的浓缩性能会得到提升，但提升幅度会变小。

从图7f可以看出，随着锥形管母线长度的继续延长，6-50号模型锥形管后方出现的漩涡与5-50号模型相比更为强烈，对模型内部的抽吸作用也更强，可使浓缩性能得到大幅提升；而由于旋涡的强度更大，导致锥形管内壁面中部偏上位置出现的流动分离与5-50号模型相比减弱，因此虽然6-50号模型的浓缩性能与5-50号模型相比，同样受到漩涡和流动分离的影响，但提升幅度会大幅提高。

图7 待选模型（β=50°）锥形管后方剖面速度矢量图

由以上分析可知，在偏转角为50°的情况下，母线长度延长，可以使锥形管后方的漩涡变得更为强烈，使浓缩性能得到提升；同时，母线的延长也会使锥形管内壁面附近容易出现流动分离，进而使浓缩性能的提升幅度降低。当母线长度延长至0.3时，开始出现轻微的流动分离；延长至0.4时流动分离的强度依然不大；而延长至0.5、0.6时，则出现了较为强烈的流动分离，使浓缩性能提升幅度降低，而浓缩风能装置优化模型的制造成本却会快速升高，因此，在偏转角为50°的情况下，选择0.4为最佳母线长度是合适的。

4 结 论

1）浓缩风能装置优化模型的浓缩性能由锥形管后方的漩涡和锥形管内壁面上的流动分离决定。漩涡的存在使浓缩风能装置优化模型的浓缩性能优于原模型。流动分离会使浓缩性能降低。

2）锥形管偏转角越小，漩涡强度越大；但漩涡强度过大，将会把锥形管外缘喷出的气流向锥形管内壁面吸引，进而影响扩散管出口处的气流径向上的扩散，使原本优越的浓缩性能降低。同时，偏转角越小，锥形管内壁面上越容易出现流动分离，也会使浓缩性能降低。浓缩风能装置优化模型的最佳状态是锥形管后方出现一个强烈的漩涡，但该漩涡的强度不至于将锥形管外缘的气流过多地向锥形管内壁面吸引，同时锥形管内壁面附近不出现强度较大的流动分离。母线长度为0.4（为中央圆筒直径）时，偏转角为50°，为最优模型，可以实现此状态。

3）偏转角为50°时，母线长度延长，可使锥形管后方的漩涡强度更大，提升浓缩性能；同时，又会使锥形管内壁面附近容易出现流动分离，降低浓缩性能。出于性价比的考虑，偏转角为50°时，0.4为最佳母线长度。

[1] Wang Wenxue, Matsubara Terutake, Hu Junfeng, et al. Experimental investigation into the influence of the flanged diffuser on the dynamic behavior of CFRP blade of a shrouded wind turbine[J]. Renewable Energy, 2015, 78: 386－397.

[2] Chong W T, Gwani M, Shamshirband S, et al. Application of adaptive neuro-fuzzy methodology for performance investigation of a power-augmented vertical axis wind turbine[J]. Energy, 2016, 102: 630－636.

[3] Aierken Dilimulati, Ted Stathopoulos, Marius Paraschivoiu. Wind turbine designs for urban applications: A case study of shrouded diffuser casing for turbines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 175: 179－192.

[4] Toshio Matsushima, Shinya Takagi, Seiichi Muroyama. Characteristics of a highly efficient propeller type small wind turbine with a diffuser[J]. Renewable Energy, 2006, 31: 1343－1354.

[5] Bontempo R, Manna M. Effects of the duct thrust on the performance of ducted wind turbines[J]. Energy, 2016, 99: 274－287.

[6] Liu Yingyi, Yoshida Shigeo. An extension of the generalized actuator disc theory for aerodynamic analysis of the diffuser-augmented wind turbines[J]. Energy, 2015, 93: 1852－1859.

[7] Vaz Jerson R P, Wood David H. Aerodynamic optimization of the blades of diffuser-augmented wind turbines[J]. Energy Conversion and Management, 2016, 123: 35－45.

[8] 韩巧丽，田德，王海宽，等. 浓缩风能型风力发电机改进模型流场与功率输出特性[J]. 农业工程学报，2009，25(3)：93－97. Han Qiaoli, Tian De, Wang Haikuan, et al. Flow field and power output characteristic of the reformative model concentrated wind energy turbine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 93－97. (in Chinese with English abstract)

[9] 韩巧丽，田德，王海宽，等. 浓缩风能型风力发电机相似模型流场特性实验―车载法实验与分析[J]. 农业工程学报，2007，23(1)：110－115. Han Qiaoli, Tian De, Wang Haikuan, et al. Test of flow field characteristics of the resembled model of concentrated wind energy turbine outside truck-mounted test and analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(1): 110－115. (in Chinese with English abstract)

[10] 田德，姬忠涛，韩巧丽. 浓缩风能装置内部流场模拟计算可靠性分析[J]. 太阳能学报，2014，35(12)：2362－2367.Tian De, Ji Zhongtao, Han Qiaoli. Reliability analysis for internal flow field simulation of concentrated wind energy device[J]. Acta Energiae Solaris Sinica, 2014, 35(12): 2362－2367. (in Chinese with English abstract)

[11] Vaz Jerson R P, Wood David H. Effect of the diffuser efficiency on wind turbine performance[J]. Renewable Energy, 2018, 126: 969－977.

[12] Coşoiu C I, Georgescu A M, Degeratu M, et al. Numerical predictions of the flow around a profiled casing equipped with passive flow control devices[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 114: 48－61.

[13] Ohya Yuji, Karasudania Takashi, Sakuraib Akira, et al. Development of a shrouded wind turbine with a flanged diffuser[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(5): 524－539.

[14] Kardous M, Chaker R, Aloui F, et al. On the dependence of an empty flanged diffuser performance on flange height: Numerical simulations and PIV visualizations[J]. Renewable Energy, 2013, 56: 123－128.

[15] Roshan Saeed Zabihzade, Alimirzazadeh Siamak, Rad Manouchehr. RANS simulations of the stepped duct effect on the performance of ducted wind turbine[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145: 270－279.

[16] Mona Abdelwaly, Hesham El-Batsh, Magdy Bassily Hanna. Numerical study for the flow field and power augmentation in a horizontal axis wind turbine[J]. Sustainable Energy Technologies and Assessments, 2019, 31: 245－253.

[17] Kishore Ravi Anant, Coudron Thibaud, Priya Shashank. Small-scale wind energy portable turbine(SWEPT)[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 116: 21－31.

[18] Heikal Hasim A, Abu-Elyazeed Osayed S M, Nawar Mohamed A A, et al. On the actual power coefficient by theoretical developing of the diffuser flange of wind-lens turbine[J]. Renewable Energy, 2018, 125: 295－305.

[19] Kosasih B, Hudin H S. Influence of inflow turbulence intensity on the performance of bare and diffuser-augmented micro wind turbine model[J]. Renewable Energy, 2016, 87: 154－167.

[20] Wong K H, Chong W T, Yap H T, et al. The design and flow simulation of a power-augmented shroud for urban wind turbine system[C]. Energy Procedia, 2014, 61: 1275－1278.

[21] 韩巧丽. 大容量浓缩风能型风力发电机模型气动特性的实验研究[D]. 呼和浩特：内蒙古农业大学，2006. Han Qiaoli. Experimental Study on Pneumatic Characteristic of the Large Capacity Concentrated Wind Energy Turbine Model[D]. Hohhot: Inner Mongolia Agricultural University, 2006. (in Chinese with English abstract)

[22] 姬忠涛，田德. 浓缩风能装置内部流场仿真计算分析[J]. 云南大学学报：自然科学版，2017，39(2)：212－218. Ji Zhongtao, Tian De. An analysis of grid independence for internal flow field simulation of concentration wind energy devices[J]. Journal of Yunnan University: Natural Sciences Edition, 2017, 39(2): 212－218. (in Chinese with English abstract)

[23] Abe K, Ohya Y. An investigation of flow field around flanged diffusers using CFA[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92: 315－330.

Optimized structural design of concentrated wind energy device based on CFD numerical simulation

Ji Zhongtao1, Tian De2

(1,,655011,;2,,102206,)

The structure of the wind concentrator will directly affect the performance of wind-concentrating turbine. In this paper, to optimize the structure, the CFD software was used. The structure was optimized by adding a new conical tube behind the diffuser of the original model, and the influence of both the generatrix length () and the deflection angle () of the conical tube on the concentrator was also analyzed. First, through the CAD software, the optimized model of a wind concentrator was built and a cylinder (diameter: 20 m; length: 30 m, coaxial with the model) was created. With the help of Boolean subtraction, the fluid field model was obtained by subtracting the optimized model from the cylinder. The patch conforming algorithm was used to mesh the fluid field and the mesh type was tetrahedral. Twenty inflation layers were divided in the thickness range of 1 cm marked on the optimization model. In the simulation, SST-turbulence model was adopted, energy equation was used and heat exchange was considered. The air velocity, temperature, density, pressure, viscosity, thermal conductivity, constant pressure specific heat capacity, flow rate, turbulent kinetic energyvalue and specific dissipation ratevalue were 10.83 m/s, 296.75 K, 1.044 kg/m3, 88 800 Pa, 1.85×10-5kg/(m·s), 0.026 22 W/(m·K), 1 013 J/(kg·K), 3 552.048 kg/s, 0.165 382 m2/s2, 11.786 s-1, respectively. The inlet boundary was the mass flow inlet, and the velocity direction was perpendicular to the inlet boundary. Both the thermal boundary conditions of the wall of the concentrator and the shell of the fluid field were at fixed temperature, with a value of 296.75 K. Pressure outlet was used as the outlet boundary. The results of flow field calculation show that the model was optimal when the generatrix length and the deflection angle of the conical tube were 0.4and 50° respectively. The concentrating performance of the optimized model was determined by the vortex behind the conical tube and the flow separation on the inner surface of the tube. The existence of vortices rendered the optimized model better than the original one. However, if the intensity of the vortices was too high, the air ejected from the outer edge of the conical tube would be attracted to the inner wall of the tube and would affect the radial diffusion of the air up-flow at the outlet of the diffuser, thus reducing the originally superior concentrating performance. Meanwhile, the flow separation also reduced the concentration performance. Conversely, if a strong vortex appeared behind the conical tube, and the flow separation near the inner surface of the tube was not so strong, the optimal condition will be reached. At this time, the generatrix length was 0.4and the deflection angle was 50°. Besides, when the deflection angle was 50° and the length of generatrix was extended, the vortex intensity behind the conical tube would increase, and the concentrating performance of the concentrator would improve. However, the flow separation was easy to occur near the inner wall of the conical tube, thus reducing the concentrating performance. But when the generatrix length was 0.3, flow separation appeared. When the generatrix length was 0.4, the flow separation was very slight. And when the generatrix length was extended to 0.5, strong flow separation occurred, dampening the enhancement of the concentrating performance. Compared with 0.5, When the generatrix length was 0.6, the flow separation was slighter. So, for cost-effective consideration, when the deflection angle was 50°, 0.4was the best generatrix length.

wind energy; computational fluid dynamics; optimization; concentrator; vortex; flow separation

姬忠涛，田 德. 基于CFD模拟的浓缩风能装置结构优化设计[J]. 农业工程学报，2019，35(24)：66－73. doi：10.11975/j.issn.1002-6819.2019.24.008 http://www.tcsae.org

Ji Zhongtao, Tian De. Optimized structural design of concentrated wind energy device based on CFD numerical simulation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(24): 66－73. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.24.008 http://www.tcsae.org

2019-08-22

2019-11-29

云南省地方本科高校联合专项-面上项目（2018FH001-053）

姬忠涛，博士，研究方向为可再生能源与清洁能源。Email：jizt123@126.com

10.11975/j.issn.1002-6819.2019.24.008

F11

A

1002-6819(2019)-24-0066-08