普朗克内插法的详细过程

吴思远 王笑君

(华南师范大学物理与电信工程学院 广东 广州 510006)

学习黑体辐射时，教材往往由于篇幅原因而简略给出成功诠释实验的普朗克黑体辐射公式．但是，作为物理教师应该跳出教材框架，对教材的内容进行深入的学习研究，了解知识发展的历史过程，以及在这个过程物理学家是如何研究思考的，进而能够利用这些材料辅助教学．在教学中引领学生经历科学家研究的过程，领会科学研究方法，养成科学思维习惯；并且在这个过程能够使学生认识到科学的本质，形成正确的科学态度、科学世界观和价值观[1]．

1 普朗克的学习经历

回顾普朗克的学习经历，有助于我们了解普朗克的研究思想，并为理解普朗克为什么能够走到使用内插法得到黑体辐射公式这一步作铺垫．

普朗克在1877年作出转入柏林大学的物理学专业的决定．在转学前，他在慕尼黑大学的老师约利(P.Jolly)劝说他，物理这一学术领域已经基本完善了，留下来研究数学吧．普朗克没有选择留下．后来他在《科学自传》中解释决定离开的原因：“通过我们思考研究后用最简单的语言阐释自然界的客观存在是最吸引我的，而且我认为最崇高的科学研究任务是探索适用于描述自然现象的规律．”[2]

在柏林大学初始的时间里，普朗克修读了著名物理学家基尔霍夫(Kirchhoff，1824—1887)和亥姆霍兹(Helmholtz，1821—1894)的课程．在学习一段时间后，普朗克表示他们的课堂不够吸引他，因此，普朗克选择自学研读感兴趣的知识．在一次偶然中，他了解到克劳修斯的著作，被他深入浅出通俗易懂的语言所吸引了．普朗克着迷于克劳修斯提出的熵的概念和其他热力学观念，从此以后普朗克全身心地投入于研究热力学当中．并且他坚信熵这个概念在物理学上会有重要的地位．这个想法一直影响着他的科学研究工作，包括后来处理黑体辐射问题的思路．

2 黑体辐射的研究成果

在1894年时，普朗克将他的研究重心转向当时德国科学研究工作热点之一的黑体辐射研究．普朗克开始从事黑体辐射研究时，在实验和理论方面都有许多杰出的物理学家从事这方面的研究．

基尔霍夫在理论上做出了阶段性的工作，提出了基尔霍夫定律和“绝对黑体”概念．将黑体辐射问题转变为寻找一个与物质无关的普适函数F(ν,T)．在此之后又知道黑体辐射的普适函数可以用平衡辐射时的能量密度ρ(ν,T)来表示[3]

式中c为真空中的光速．接下来的工作就是要探寻能量密度函数．在探寻能量密度函数上维恩作出了杰出的贡献，给出了能量密度函数的基本形式

(1)

式中A是常量，其中φ的函数形式尚不能最终确定．

在1896 年，维恩为了能够得到确定的能量密度函数，在推导时作出了3个假设．

第一，假设温度T的黑体辐射可以与同温度的理想气体比拟，并且引用麦克斯韦速度分布律．

第三，假定辐射能量密度与相应的分子数成比例[3]．

最终得出能量密度函数，也称为维恩公式

(2)

式中a和b是常数．

3 普朗克对维恩定律的改进

普朗克完全知道维恩于1896年得到的公式，而且这个公式极好地反映了当时实验的观测结果．但是维恩在推导公式时所作的假设不符合普朗克的口味，是因为普朗克在很长一段时期里都不相信玻尔兹曼的分子动理论观点．比起那种困难而又带有近似性质的分子动理论来说，他更喜欢纯热力学的严密理论．

因此，普朗克希望通过热力学方法使用更少的假设得到相同的方程．在这个问题上普朗克认为熵是关键所在．在给定体积具有一定能量的空腔中，平衡辐射能量分布是各种可能分布中最稳定的，其熵值最大．空腔辐射平衡时的能量密度函数可以通过熵S与振子平均能量U之间的函数关系得到．

首先，普朗克运用经典电磁理论对封闭在一个具有理想反射壁的空腔里的电磁辐射进行研究，采用赫兹振子模型，由运动方程出发[4]导出能量密度ρ(ν,T)与振子平均能量U的关系式

(3)

接着，普朗克为了找到振子的熵S与它平均能量U的关系，利用了维恩公式(2)与能量密度公式(3)，得出振子平均能量的表达式

(4)

(5)

(6)

(7)

得出这个简单的关系后，普朗克坚信他走在正确的道路上．后来他提到：“黑体辐射研究就是在寻找一条普适的物理定律，并且越是普适的物理定律就应该越简单……所以当我得出量R与振子的平均能量成正比时，就知道了它是解决能量密度函数的关键．”[5]

最终，对式(5)积分可得熵与振子平均能量之间的关系

(8)

在普朗克的上述论证中，似乎存在着利用维恩公式定义振子的熵，而后又用这个熵定义式得出维恩公式的循环推论．实际上普朗克的做法只是把维恩公式作为关于能量密度函数的一个经验猜测，从这个公式所提供的信息来建构一个振子熵的定义式作为一个基本假设，然后由系统熵变出发，给辐射规律一个严格的理论论证．普朗克在1899年5月18日提交论文展示了他的研究成果，并表示确信从他的假设中推导出的辐射定律是正确的[5]．

4 普朗克由内插法得到辐射公式

普朗克在通过简单的假设重新推导出维恩公式后，与实验物理学家保持紧密联系，及时了解最新的实验进展．在1899年底，普朗克了解到卢默尔(O.R.Lummer，1860—1925)等实验物理学家发现了在把波长范围扩大后维恩公式对实验结果存在偏差[7]，于是开始重新思考研究维恩公式．

与此同时，瑞利(Rayleigh，1842—1912)在知道维恩公式在长波方向偏离的实验结果后，使用麦克斯韦-玻尔兹曼的能均分定理对黑体辐射进行研究[8]．在1900年6月，瑞利发表题为《关于完全辐射定律的评论》的文章，在文章中瑞利根据能均分定理提出了自己的辐射公式，即有名的瑞利公式[6]

ρ=Cν2T

(9)

式中C是常量．

U=const·T

(10)

(11)

(12)

在总结式(7)和式(12)时可知函数R有两个简单的极限情况：在小能量时，函数与能量一次方成正比；在大能量时，函数与能量的二次方成正比．为了得到普适的情况，选择函数R等于能量的一次方和能量的二次方之和[3]

R=C1U+C2U2

(13)

(14)

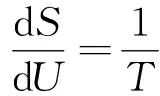
(15)

由式(15)积分后即可以得到振子平均能量的表达式

(16)

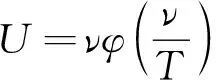
(17)

再将式(17)代入式(3)，即可得到辐射能量密度公式

(18)

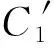
在得出黑体辐射公式后，普朗克就将公式交给鲁本斯与实验数据作比较．两天过后，鲁本斯亲自来到普朗克家里告诉他公式与实验结果一致．紧接着普朗克将他的研究工作写成报告，并于1900年10月19日在德国物理学会上进行汇报．自此过后，普朗克的黑体辐射公式经受住了考验，被更多精密的实验证实是正确的．

5 总结

通过上述的历史探索，给出普朗克内插法的详细过程，进而弥补教材上只有结果，没有研究过程的遗憾．使教师能够在教学中融入物理学史，进而使学生发现普朗克内凑出黑体辐射公式并不是像通常理解的那样理所当然，而是经历了科学家们曲折反复的研究才完成的．同时使学生感受科学家的实际创造过程和领会其研究思想，有利于促进学生形成严谨科学的物理思维，并且大大激发学生对更深奥的物理知识的探究热情．