基于二面角逆插值Loop细分的渐进传输方法
史 卓,孔 谦,玉 珂,蓝如师,罗笑南
基于二面角逆插值Loop细分的渐进传输方法
史 卓,孔 谦,玉 珂,蓝如师,罗笑南
(桂林电子科技大学艺术与设计学院,广西 桂林 541004)
随着虚拟现实、增强现实等领域快速发展,渐进传输获得了良好的用户体验。为了三角网格在移动终端的快速传输和显示,提出了一种基于二面角逆插值Loop细分(DRILS)的渐进传输算法。主要通过对原始三角网格进行基于二面角插值Loop细分(DILS)和插值Loop细分(ILS)进行预处理,在局部特征精确保持的同时获得具备细分连通性的精网格。在渐进传输的过程中通过对该精网格迭代操作3个步骤,即奇偶顶点划分、预测偏移量、更新三角网格。由于采用DILS与ILS结合获取精网格,在渐进传输的过程中保持了精确的局部特征,同时也加快了渐进传输的速度。实验对比表明,该算法精确、高效,适应于移动终端设备的显示传输及存储。
渐进传输;逆细分;插值Loop细分;二面角
渐进传输在视频动画、游戏、三维建模等领域具有广泛地应用价值。渐进网格在渐进传输中是具体内容表现形式,HOPPE[1]首次提出的采用基于顶点分裂生成渐进网格,为三维网格在多分辨率渐进传输过程中受限于存储空间及传输带宽的影响提供了解决方案。通常情况下,科研人员采用基于QEM (quadric error metrics)[2]算法在边折叠、点分裂等改进方法进行三角网格简化和生成多层次的三角网格模型。随着三角网格细分方法的深入研究,逆细分[3]的提出使得细分在渐进网格生成得到了发展。文献[4]提出了基于逆蝶形细分算法对三角网格进行渐进传输;文献[5]在此基础上提出修改细分模板为Loop细分[6],同时不再对上一层网格留下来的顶点进行补偿计算的逆Loop细分算法,虽然逆Loop细分算法相对于逆蝶形细分算法计算量小,但由于Loop细分是逼近型细分,无法完成保持局部网格特征,网格将会产生凹陷收缩等问题。文献[7]根据插值Loop细分算法[8]并采用其算法对该类问题进行了解决,使得渐进传输过程中生成的渐进网格能够更好地重建。但在获取精网格的过程中,此类方法由于采用相应的细分算法对其进行细分连通性处理,在数次细分之后,三角网格细分消耗代价将呈指数级上升,无法完成局部特征要求十分精细的网格处理。文献[9]提出的一种基于DM (delaunay mesh)的简化算法,该算法虽然简化速度很快,但无法完成渐进传输功能。
本文在获取渐进传输精网格的过程中,提出基于二面角逆插值Loop细分算法。其与插值Loop细分算法结合可对初始网格进行处理,该类算法采取二面角插值Loop细分算法通过对三角面片两两之间夹角阈值做判断,并按照一定的细分规则进行局部细分。由此可以使局部特征明显的部分更加精细,而平滑部分则不再进行过多的增加顶点和边的信息,再通过插值Loop细分算法对其做细分连通性补偿,此方法更加高效、精确。在获取渐进传输精网格之后,采用奇偶顶点划分、预测偏移量、更新三角网格循环操作,直到三角网格无法再分裂为止。最终生成一个粗网格和一系列偏移量组成的渐进网格。本文算法在奇偶顶点划分过程中将原有插值Loop细分算法过程中分层生成边点作为冗余信息进行删除,通过更多的控制顶点,实现边缘的插值点对中心顶点的补偿。此算法在保持网格模型整体特性的同时,增强局部特征信息,由于比传统逆细分算法计算网格顶点数少,在计算量上也有大幅的降低,在实际应用过程中更加有效。
1 渐进网格编码规则
1.1 插值Loop细分和逆细分
曲面细分主要分为逼近型细分和插值型细分。在处理三角网格细分算法上,逼近型细分典型模式为Loop细分,插值型细分典型模式为Butterfly细分。该类细分算法均为渐进生成三角网格。如Loop细分规则,在每条边上加一个新的顶点作为边点,原来的顶点根据该边点权重重新调整顶点位置。由于传统Loop细分是逼近型细分,在奇异点处会产生收缩问题。为解决该类问题,结合插值型细分Butterfly模板对奇异点处理方法,首先通过扩大Loop细分的模板(图1),实现边缘插值点对中心点的补偿。
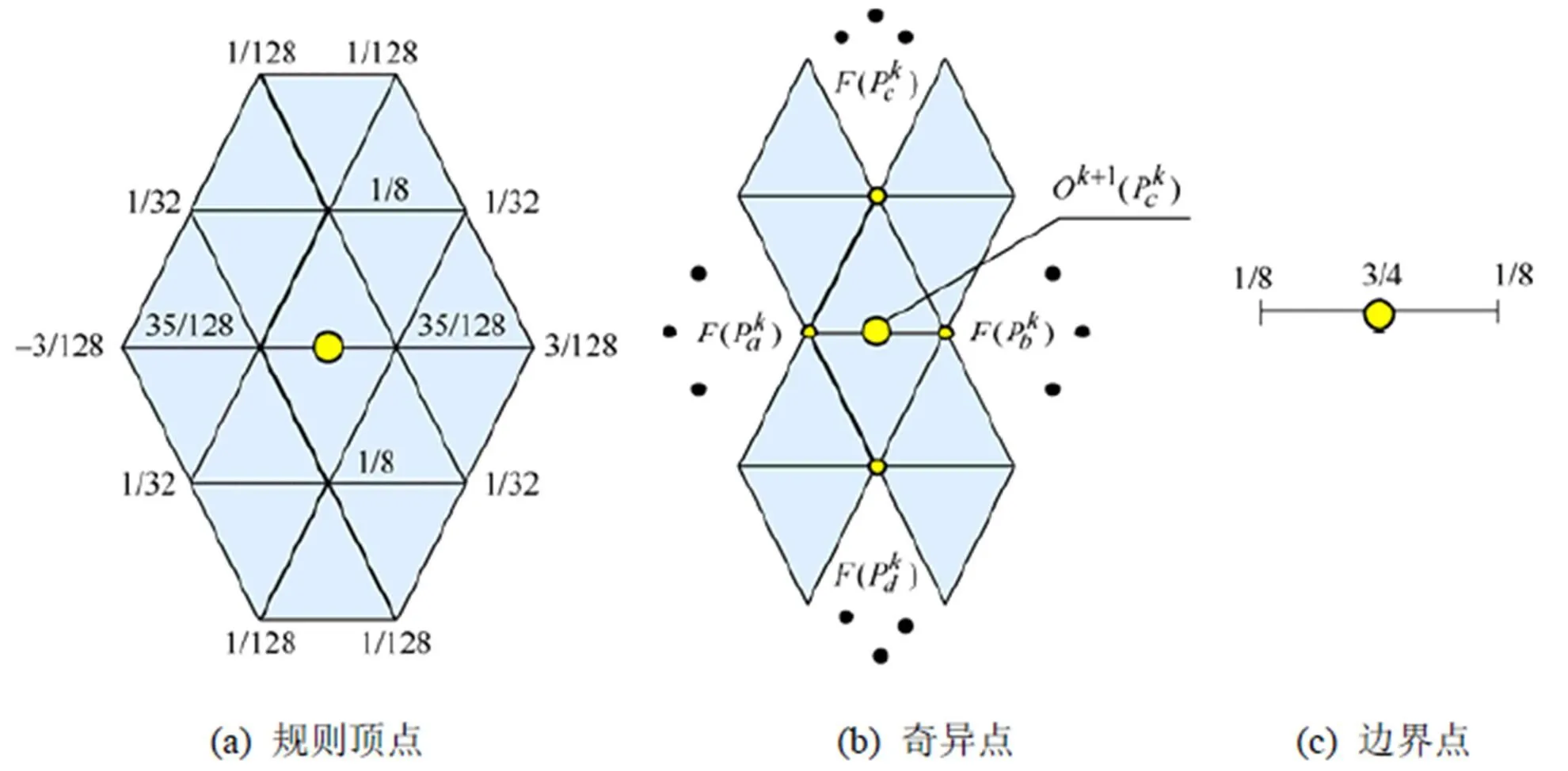
图1 插值Loop细分模板
再根据改进的Butterfly细分对奇异点处理方法,修改传统Loop细分处理奇异点规则,解决收缩凹陷问题。
将新生成的边点定义为奇点Odd,原始顶点重新调整后可定义为偶点Even。其中由于奇异点是特征保持顶点,也定义为偶点。

当偶点Even为正则顶点时(度为6的顶点),插值Loop细分的奇点Odd的计算模板为
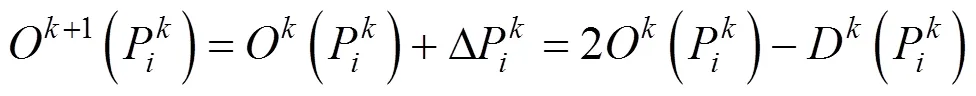



当偶点Even为奇异点时,非边界顶点的模板为
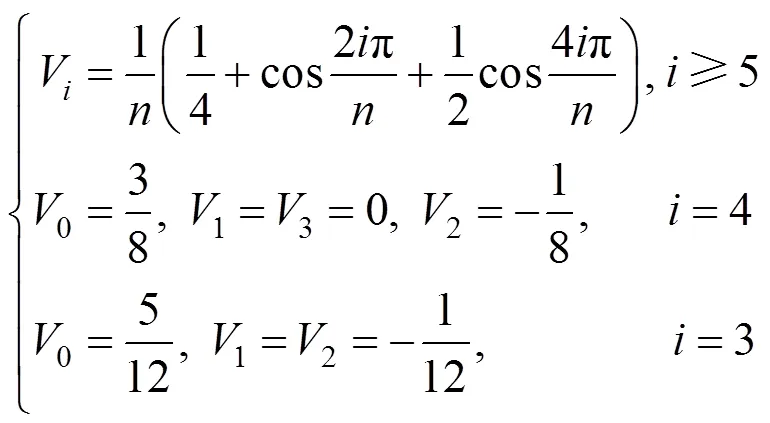
其中,为顶点的度,与改进的蝶形细分的奇异点处理方法类似。
通过仔细分析插值Loop细分顶点生成规则发现偶点。偶点集中的顶点均为控制顶点,其在插值Loop细分的过程中保持不变,此特征可在逆细分过程中作为特征顶点保存下来。而奇点是细分过程中生成的顶点,根据奇点生成计算公式可看出并未对偶点位置产生影响,可以作为冗余顶点在逆插值Loop细分过程中删除。
1.2 二面角细分规则
传统的Loop细分算法是对三角网格进行1-4分裂,该算法将导致三角面片及顶点个数呈几何式增长,经过几次细分后再对三角网格进行细分平滑处理将会产生时间和内存方面更高的代价,不利于多分辨率渐进网格移动传输。自适应细分有很多方法,如基于GPU的特征自适应细分算法[10-11],其在GPU上运行,运行环境受限;基于顶点曲率特征[12]算法,其实现比较复杂;判定面片向量夹角[13]提出类似算法,但其仅针对于传统的Loop细分,对插值Loop细分并未进行改进,依然存在收缩问题。为解决该类问题,本文提出基于二面角细分规则,可高效获得在保持局部特征的同时又具有平滑处理效果的三角网格。
通常一个三维模型具有明显局部特征,即曲率较高的顶点,在渐进传输的过程中,该类特征是需要保留的。而平滑部分则在初始网格或者细分数次后达到区域平滑后三角片面无需再次进行1-4分裂,减少计算量及运算时间。本文提出的基于二面角夹角判断准则来划分细分规则算法步骤如下:
步骤1.创建2个空集Fsmooth和Fsteep,其中集合Fsmooth存储三角网格中的平滑面,集合Fsteep存储陡峭面。
步骤2.计算所有三角面片的法向量(= 1,···,为三角网格中面片个数)。
步骤3.计算所有相邻两面的向量夹角,其中每个面片均有3个共边面片。可标记其两两法向量夹角分别为,,,同时设定一个夹角阈值为。
步骤4.分别判断一个三角面片相关的3个向量夹角,,与阈值的大小关系,如果小于该阈值,则将相应面片存入集合Fsmooth中,否则存入集合Fsteep。面片的细分规则根据阈值的大小来确定。
步骤5.迭代操作步骤4,直到所有的三角面片均判断结束。
步骤6.对集合Fsmooth集中的面片不进行细分处理,对集合Fsteep集进行细分处理。
1.3 渐进网格生成原理
在三角网格中,一个顶点的度表示为与该顶点相连接边的个数。正则点表示度为6的顶点,非正则点或奇异点表示度不为6的顶点。正则网格定义为所有的顶点都为正则点,该类三角网格很少有现成的;大部分顶点为正则点,存在少数非正则点的三角网格定义为半正则网格。而对于非正则点过多造成无法实现逆插值Loop细分的模型,其不具备细分连通性,可通过重新三角化或再次细分使其达到符合要求的网格。
根据逆细分规则,要求生成的三角网格为正则网格或半正则网格,即具备细分连通性,且必须满足

传统的细分准则生成的顶点大部分为正则点,而根据二面角Loop细分顶点生成准则,可知在下一层顶点生成的过程中可能会产生一定量的非正则点,如图2所示。

图2 二面角规则产生非正则点
在解决上述问题时,考虑到二面角规则细分在保持局部特征的同时快速完成细分,在渐进网格传输过程中具有一定的价值。因此二面角规则结合插值Loop细分获取精网格具有一定的必要性。
将一个粗网格通过二面角规则细分若干次之后,再进行插值Loop细分,获得的精网格既保持了局部特征的尖锐性,同时在效率方面得到提升,也满足了其精网格通过逆细分算法渐进传输。
2 渐进网格传输算法
根据渐进网格生成原理,生成的精网格可对其进行渐进传输。其渐进传输算法步骤如下:
步骤1. 奇偶集顶点迭代分裂。

图3 奇偶顶点分布情况
初始化偶点集E和奇点集O(0≤≤)。其中偶点集E是正则点或奇异点,假设将顶点划分至偶点集E;由于奇点集O是新生成的顶点,且是冗余顶点。根据细分准则,偶点对应的奇点为其邻接的所有顶点,其划分在奇点集中,任取一点为,设点关于点对称的顶点,顶点划分至偶点集E,依次迭代划分,直到所有的顶点全部划分到奇点集O或偶点集E中。
具体划分算法如下:
Bool setEven (){
将归并到偶点集E中;
遍历所有与相邻的顶点{
返回false;
否则将并入奇点集O;
找出与关于对称的顶点;
调用setEven ();
}
返回true;
}
步骤2. 顶点预测,计算顶点偏移量。


步骤3. 更新三角网格。
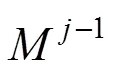
3 实验结果与分析
本算法用C++实现,采用的环境包括:CPU:E5 3.5 GHz;内存:16 G。其中获取二面角Loop细分模型是通用双系统Linux环境下编程完成,渐进传输三角网格生成程序在Windows下利用开发工具Visual Studio 2013及CGAL库完成。
首先通过二面角插值Loop细分算法获取初步精网格模型,如图4所示,设二面角夹角阈值为20°,局部特征通过细分更加明显,而基本平滑部分则不再增加额外的顶点及边的信息。其算法比插值Loop细分算法在时间上有明显优势,同时也为生成精细渐进网格做好了前期处理,减小了巨大的运算开销。
图4的前两行为Dragon的三角网格细分处理示意图。图4(a)为对初始图进行5次插值Loop细分层次图,(b)为对初始图进行5次二面角插值Loop细分层次图;图4(c)和(d)分别对应图4(a)和(b)的模型渲染图。由渲染图可以看出,在第5层之后,两者的渲染结果基本上相同。

图4 Dragon(1 000面片)三角网格及渲染分层图
由表1可知,插值Loop细分算法新增加的网格数呈指数式增长,在精细网格的获取中代价巨大。而随着网格数的增多,二面角插值Loop细分算法获得网格的速度更快。由此可以采用二面角插值Loop细分算法获得的网格为渐进传输精细网格做预处理。

表1 Dragon不同细分算法运行时间对比
在获取渐进传输最精细网格的过程中,采用二面角插值Loop细分规则后再进行插值Loop细分获取的网格与仅采用插值Loop细分规则获取的网格,通过使用网格误差评估软件Metro (v4.07)对误差进行测量并对运行时间进行对比,如图5所示。

图5 获取渐进传输精密网格
表2中,E0为Ellipsoid初始网格,E1为图5 (b)生成的精密网格,E2为图5(c)生成的精密网格。具体时间与距离误差分析见表2。

表2 Ellipsoid网格误差分析及时间对比
在Hausdorff距离误差极小的情况下,表2采用二面角插值Loop细分再进行插值Loop细分,大幅度提高了计算速度,同时消耗较短时间生成模型,有助于后续渐进传输。而仅采用插值Loop细分算法不仅消耗大量时间,在细分后期也将会带来巨大的运算开销,无法完成快速渐进传输功能。
在渐进传输的过程中,通过将DM、逆蝶形细分(reverse butterfly subdivision,RBS)与二面角逆插值Loop细分(dihedral reverse interpolation Loop subdivision,DRILS)算法在运行时间及渐进传输可行性上进行对比,如图6所示,DM算法在经过数次传输之后,三角网格仅保存局部网格形式,且无法表达原有模型形状,并未实现渐进网格的重建工作,也无法完成渐进传输及显示。

图6 多分辨率渐进网格生成显示
根据图6多分辨率渐进网格生成显示和表3的Hausdorff误差分析,逆蝶形细分算法与二面角逆插值Loop细分均达到了渐进传输功能。

表3 Bear多分辨率渐进传输时间对比及误差分析
从表3的传输时间上看,RBS算法在渐进传输的过程中耗时长,用户体验较差。而DM算法虽然在传输时间上有一定优势,但根据图6 (g)运行2次后获取的三角网格已经无法准确地显示原有网格所具备的拓扑结构,无法给用户带来多分辨率体验。
4 结束语
本文提出一种采用二面角插值Loop细分规则与逆细分算法结合的渐进网格传输算法。描述了逆细分准则以及通过顶点分裂、预测偏移量和更新网格3个步骤获取渐进传输网格,在渐进传输过程中具有保持局部特征及高效传输等特点。通过实验对比,采用二面角插值Loop细分规则与插值Loop细分混合算法,使网格达到具有细分连通性,满足逆细分准则。该网格在多分辨率渐进传输过程中具有高效、局部特征明显的特点,符合算法设计初衷。该算法的主要特点如下:
(1) 在获取精网格过程中采用二面角插值Loop快速、精确的特点,混合插值Loop细分算法达到渐进传输网格要求。避免了传统的细分算法在获取精密网格的巨大计算量。
(2) 提出顶点分裂、根据细分模板预测偏移量、更新网格3步骤对符合渐进传输的精密网格进行渐进传输,避免了像逆蝶形细分算法使用顶点仿射组合对偶点补偿的计算,加快了渐进传输的效率。
(3) 采用以插值Loop细分算法为模板,较传统的逼近型Loop细分算法可避免模型凹陷缺点,保持了模型的局部特征。
通过大量的实验结果表明,采用基于二面角逆插值Loop细分渐进传输算法效率高、局部特征明显,给用户在终端产品上快速渲染及视觉显示带来更多真实感,比以往算法更加高效、精确,具有一定的应用价值。
[1] HOPPE H. Progressive meshes [C]//Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1996: 99-108.
[2] GARLAND M, HECKBERT P S. Surface simplification using quadric error metrics [C]//Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1997: 209-216.
[3] HASSAN M F, DODGSON N A. Reversesubdivision [M]//Advances in Multiresolution for Geometric Modelling. Berlin: Springer-Verlag, 2005: 271-283.
[4] LUO X N, ZHENG G F. Progressive meshes transmission over a wired-to-wireless network [J]. Wireless Networks, 2008, 14(1): 47-53.
[5] MA J P, LUO X N, CHEN B, et al. Triangle mesh compression based on reverse subdivision for mobile terminals [J]. Journal of Software, 2009, 20(9): 2607-2615.
[6] LOOP C. Smooth subdivision surfaces based on triangles [D]. Salt Lake City: University of Utah, 1987.
[7] SHI Z, AN Y, XU S, et al. Mesh simplification method based on reverse interpolation Loop subdivision [C]//Proceedings of the 8th International Conference on Computer Modeling and Simulation. New York: ACM Press, 2017: 141-145.
[8] SHI Z, LIN S J, LUO X N, et al. Interpolatory and mixed Loop schemes [J].Computer Graphics Forum, 2008, 27(7): 1829-1835.
[9] LIU Y J, XU C X, FAN D, et al. Efficient construction and simplification of Delaunay meshes [J]. ACM Transactions on Graphics (TOG), 2015, 34(6): 174.
[10] NIEßNER M, LOOP C, MEYER M, et al. Feature-adaptive GPU rendering of Catmull-Clark subdivision surfaces [J]. ACM Transactions on Graphics (TOG), 2012, 31(1): 6.
[11] HUANG Y C, FENG J Q, NIEßNER M, et al. Feature-adaptive rendering of Loop subdivision surfaces on modern GPUs [J]. Journal of Computer Science and Technology, 2014, 29(6): 1014-1025.
[12] 吴剑煌, 刘伟军, 王天然. 面向三角网格的自适应细分[J]. 计算机工程, 2006, 32(12): 14-16.
[13] AMRESH A, FARIN G, RAZDAN A. Adaptive subdivision schemes for triangular meshes [C]//Hierarchical and Geometrical Methods in Scientific Visualization. Berlin: Springer-Verlag, 2003: 319-327.
[14] PASCUCCI V, BAJAJ C L, ZHUANG G. Single resolution compression of arbitrary triangular meshes with properties [C]//Proceeding of the Conference on Data Compression. Washington, DC: IEEE Computer Society Press, 1999:247.
[15] MONGKOLNAM P, RAZDAN A, FARIN G. Lossy 3D mesh compression using Loop scheme [C]//Proceedings of the 6th IASTED International Conference on Computer Graphics and Imaging. Anaheim: ACTA Press, 2003: 64.
[16] LEE A W F, SWELDENS W, SCHRÖDER P, et al. MAPS: Multiresolution adaptive parameterization of surfaces [C]//Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1998: 95-104.
Progressive Transmission Method Based on Dihedral Reverse Interpolation Loop Subdivision
SHI Zhuo, KONG Qian, YU Ke, LAN Ru-shi, LUO Xiao-nan
(School of Art and Design, Guilin University of Electronic Technology, Guilin Guangxi 541004, China)
With the rapid development of virtual reality, augmented reality, etc., Multi-resolution progressive transmission can provide a good user experience. In order to implement the fast transmission and display of triangular mesh in the mobile terminal, this paper presents a progressive transmission algorithm based on dihedral reverse interpolation Loop subdivision (DRILS). The algorithm mainly uses dihedral interpolation Loop subdivision (DILS) and interpolation Loop subdivision (ILS) algorithm processing. A fine mesh with subdivision connectivity is obtained at the same time as the local feature is accurate. In the process of progressive transmission, three steps are taken for the iterative operation of the accurate triangular mesh: odd and even vertex partition, offset prediction, and triangular mesh prediction. Due to the combination of the DILS and ILS which is used to obtain accurate mesh, the local characteristics of the progressive transmission are accurate, and the speed of progressive transmission is also accelerated. The experimental comparison shows that the algorithm is accurate and efficient, and is suitable for display, transmission and storage of mobile terminal devices.
progressive transmission; reverse subdivision; interpolation Loop subdivision; dihedral
TP 391
10.11996/JG.j.2095-302X.2019010092
A
2095-302X(2019)01-0092-07
2018-07-27;
2018-09-18
广西信息科学实验中心开放基金项目(YB1506);国家自然科学基金项目(61862018);广西自然科学基金项目(2018GXNSFAA138084);广西高校图形图像重点实验室开放课题(GIIP201404)
史 卓(1978-),男,江苏常州人,副教授,博士,硕士生导师。主要研究方向为图形图像处理、数字媒体。E-mail:shzh@guet.edu.cn
玉 珂(1979-),女,广西柳州人,研究实习员,本科。主要研究方向为图形学、虚拟现实。E-mail:xiaoxiao-yk@163.com

