热测地场控制的近似刚性网格变形技术
邵茂真,寿华好
热测地场控制的近似刚性网格变形技术
邵茂真,寿华好
(浙江工业大学理学院,浙江 杭州 310023)
为保持三维模型局部细节,修正近似刚性网格变形算法(ARAP)应用于大尺度以及非完全刚性变形中出现的扭曲、翻折问题,提出了一种基于测地场约束的近似刚性变形方法。首先对模型进行Laplacian变形,并通过奇异值分解求得局部单位的旋转矩阵,计算模型刚性变形能量;然后通过求解稀疏线性系统,更新变形点,再通过求解两次稀疏线性系统,计算变形过程中产生的测地场偏差,并修正变形网格,得到与原始网格测地场接近的变形结果;反复迭代上述步骤,直到热测地场偏差满足一定要求,获得最终变形结果。结果表明,该方法能在网格变形过程中快速地完成网格点修正功能,在应用于大尺度变形中也能有效地避免网格出现翻折问题。
近似刚性变形;热测地场;稀疏线性系统;翻折
随着近年来计算机图形学飞速发展,三维几何模型尤其是三角网格模型在动画、游戏、3D打印、电影等相关领域得到了广泛应用。三角网格变形作为常用的一个几何处理工具,能根据用户的交互操作,对原模型进行变形,以表达用户特定的创作 意图。
网格变形一直是计算机图形学中较为活跃的一个方向。本文只讨论与微分域的网格变形方法相关的方法以及所用的一些思想和概念。
微分域网格变形实质上是一个用微分坐标描述网格变化的问题,其是非线性问题,因为微分坐标是非线性的依赖顶点位置。Laplacian变形[1-4]方法已经得到了广泛的发展,可通过保持变形前后的Laplacian坐标来保持局部细节,但其变形均需对旋转变形加入约束或定义[5]。另一种解决旋转变换的方法,是从保持局部的刚性入手以保持局部细节,使用ARAP能量体现,在几何处理中得到了广泛的应用。基于此能量,SORKINE和ALEXA[3]提出了一种网格变形方法,只需要控制顶点的约束,整个变形就能自动的完成,并且局部的旋转变换也能自动地在迭代优化中产生。该变形方法近年来在效率[6]和效果[7]上得到了发展。
ZHOU等[4]引入体积图Laplacian算子,将三角网格内部与表面巧妙地联系起来,使得变形后的图形能较好地保持原有体积,同时能够很好地避免曲面的自交。通过类似泊松变形的传播方法将控制曲线的变换显式地传播到兴趣区域,最后通过线性变分的方法求解变形网格。文献[8]将该方法简化后应用到近似刚性网格变形之中,实现了保细节以及整体近似刚性的变形。文献[9]另辟蹊径,以三角形与坐标原点构成的四面体的有向体积加权和表示模型体积。通过将模型的刚性保持和体积保持转化为网格顶点位移的约束求解,实现三维物体的近刚性保体变形。
GAO等[10]用L1范数代替传统的L2范数优化ARAP能量函数,使得扭曲处得到减少,且更好地保持几何特征。文献[7]将旋转差项加入到ARAP能量函数中,实现了相对刚性旋转的光滑处理。CHAO等[11]将1-邻域的ARAP能量框架扩展到2邻域上,得到了一个连续的ARAP能量框架。CHEN等[12]将此邻域扩展为任意大小的并且内部可以存在多种邻域结构的ARAP能量框架,实现了刚性可控的ARAP网格变形技术。
AU等[13]将等值线和刚性信息与控制点(handle)联系起来,提出了一种控制点等值线引导的网格编辑手段与本文方法较为相似。CRAME等[14]巧妙地将热传播与测地距离两者联立起来,将热传播方向认为是测地距离的负梯度方向,极大地提高了求源点到网格上其他点距离所需的时间。本文认为在近似刚性的网格变形中,变形前后对于源点的测地距离标量场(测地场)应该是大致不变的,此观点在做近似刚性变形的迭代过程中得到了佐证,同时,测地场也在不断地逼近变形前网格测地场。
1 本文算法框架
传统的ARAP变形技术只能保证相连顶点之间的刚性结构,这使得在变形的过程中不相连顶点之间会发生较大的拉扯从而改变原来的测地距离,如图1所示。

图1 网格变形前后测地距离路径发生改变
针对此现象,本文提出了一种测地场约束的ARAP网格变形技术。且分别采用刚性变形能量E和测地场变形能量E衡量曲面的刚性变形误差和距离场误差。相应地,模型的变形过程即是最小化变形能量的过程,即
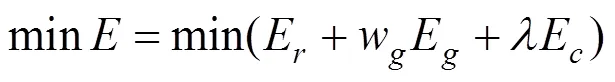
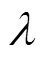

2 热测地场控制的ARAP网格变形
2.1 ARAP网格变形技术[3]
当给定一个三角网格,其主要拓扑结构由个点和个三角形构成。()为与顶点相连的所有顶点的集合,称为1-邻域顶点。
ARAP变形算法定义网格顶点与1-邻域的顶点和边构成刚性变形单元,每个相似大小的变形单元重叠地覆盖整个网格表面。变形的过程假设所有的变形单元只发生刚性变换,即


整个变形区域的能量函数是每个变形单元的能量函数之和,即






一般的网格变形就在ʹ预定义部分约束点,其中包括静态不变动的点与主导变形的控制点(handle vectices),一般由用户交互地给定
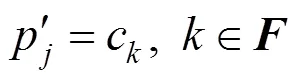
反复迭代上述的和,如此反复迭代直到能量误差达到一定的阈值或趋于稳定为止。
2.2 热测地场[14]
文献[14]提出了利用热运动方程来计算网格测地线的方法,即当一根烫的针尖接触到曲面上的一点时,热量会随着时间的推移而扩散,测地距离因此可以和热运动相联系。
热测地线算法步骤如下:
输入:热源点v。
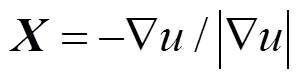
步骤3. 得到测地距离的梯度之后,测地线的问题即为
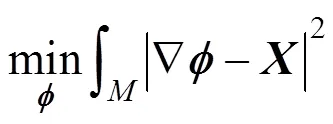
根据变分法,式(8)最小化即为求解泊松方程
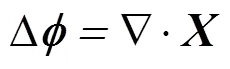
应用在三角网格中时,通过离散化处理,只要求解两次稀疏线性方程组,在时间和效率上均有较好的改进。
本文将每个顶点到热源点测地距离构成标量场简称为热测地场,如图2所示。
本文提出假设:近似刚性网格变形前后的热测地场也是近似不变的,在此基础上观察近似刚性网格变形过程中热测地场的变化,此时变形非完全刚性的变形,发现热测地场也以较为缓慢的速度逼近变形前网格测地场,如图3所示。
在上述例子中近似刚性网格变形迭代5次后,近似刚性能量已经趋于不变,如果按原先的标准图3(b)当作最终的变形结果输出,本文对其继续迭代并做测地场观察发现,尽管其近似刚性能量不再变小反而会出现微微增大的情形,但其测地场能量仍在持续减小,并在迭代30次时达到收敛,此时测地场与原测地场的差异已经非常小。

图2 标准兔子模型的热测地场

图3 ARAP算法测地场差异图
(黑色圆点为变形控制点,其中橘色越深代表该处测地距离差异越大,蓝色则表示该处测地距离没有发生变化)
2.3 热测地场控制的ARAP能量函数构造
针对上述观察结果,本文提出了一种新的测地场控制下的近似刚性网格变形技术。
采用距离场差的和表示热测地场变形能量
将其带入式(1),则原问题就变成最小化总能量函数


2.4 热测地场控制的ARAP模型框架
本文在非完全刚性的变形应用ARAP网格变形技术时,其近似刚性变形能量并非向0收敛,相反会收敛于一个较大的常数。此时三角网格的边长有很大一部分发生了伸缩变换,影响能量函数对输出结果的一个判断,因此采用式(11)作为新的能量函数,其中w取较大常数时,该能量函数具有收敛性,同时定义变形终止条件为

本文算法步骤如下:
输入.起始三角网格,控制点,热源点v。
输出.变形后网格。

步骤2. 根据所得和式(6)更新。

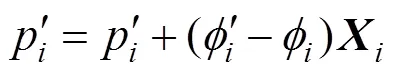
源点的选择直接决定了其他点的测地距离,以及测地场修正过程中的导向。若选用控制变形的控制点作为源点,修正过程将在修正测地场的同时,其他参与修正的顶点也将向变形最终位置逼近,加入测地距离修正能加快变形收敛速度的原因也在于此;若选用其他参与变形的顶点,由于该顶点自身存在随机偏差的原因,最终修正虽然能够修复网格内部折叠现象,但会导致整体变形都加入随机偏差,该偏差会在下次ARAP变形中修正,一个不好的源点选择可能导致网格变形消耗更多的时间。若选用不动点作为源点,同参与变形点一样极有可能变形减慢,增加时间 成本。
测地场约束是如何修正网格内部折叠的呢?
网格内部折叠的根本原因在于ARAP网格变形过于强调cell结构的不变性,为了能达到此效果,当发生非刚性变形或大幅度变形时,会以折叠和拉伸的方式来保证cell结构的近似不变,在此情况下ARAP的能量消耗最小。而折叠区域的另一直观结果,就是到某一源点的测地距离场发生了极大变化,即改变了原先的测地距离分布。图8(b) Tyra模型尾巴部分可以直观地看到这一现象。
式(13)以前一次变形的测地场梯度方向作为修正方向,测地距离的差值作为修正值,重新定位顶点位置,不改变原拓扑结构,近似地得到与前一次测地距离场分布相同的变形结果。
3 实验结果与分析
本文算法运行环境为:Windows 7,i5-4590CPU@3.30 GHz,4 GB。且在Visual Studio 2012上实现的,稀疏线性方程组和矩阵的奇异值分解使用的均是Eigen库,为了加快线性方程组的求解过程,对所有方程组的求解均用了基于Cholesky分解的解法。
图4为本文算法在测地场差异变化过程,并与图3进行比较,还以折线图(图5)的方式展示了两者的迭代收益。
本文算法以热测地场为约束进行网格的重新排列,对每次迭代出现的畸形网格做优化处理,以保证每次迭代所得网格拓扑结构不发生变化,同时在一定程度上缩减了ARAP变形所需的时间。图6(b)展示了在第5次ARAP变形迭代时Armadillo鼻子处出现的畸变,此时其热测地场能量高顶点主要分布在Armadillo上部分。通过本文算法对Armadillo进行热测地场修正,有效地消除了在鼻子处的畸变问题,同时其热测地场也与原形状的热测地场趋于接近。
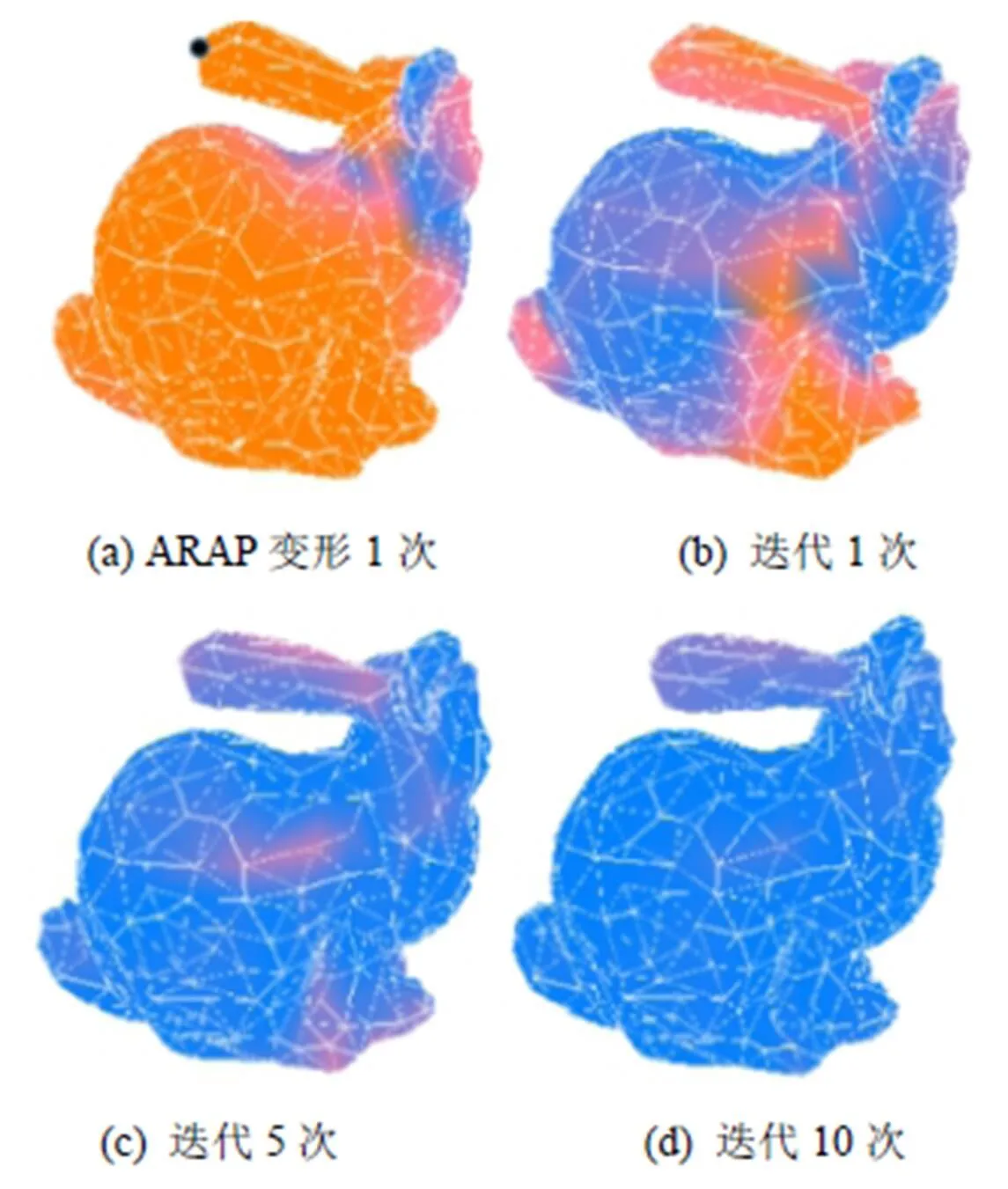
图4 本文算法测地场差异图
(黑色圆点为变形控制点,其中橘色越深代表该处测地距离变化越大,蓝色则表示该处测地距离没有发生变化)

图5 Bunny变形Eg变化对比图
对尾巴、脚这类动画常用变形进行观察(图7),当出现大角度的非完全刚性变形时(图中尾巴部分),ARAP变形极其容易发生改变网格内部翻折的情形。图7红色框内为不参与变形网格顶点,红色顶点为控制点,将其分别变形到蓝点位置,ARAP算法和本文算法均迭代8次。可以看到图7(b)中在尾巴位置发生了网格折叠的情形,这是由于ARAP对大尺度、非完全刚性变形的缺点。而本文算法则很好地解决了这一问题,如图7(c)所示。图8为Tyra尾部网格对比图,图9为Cactus变形对比图。

图6 Armadillo变形对比图

图7 Tyra变形网格对比图
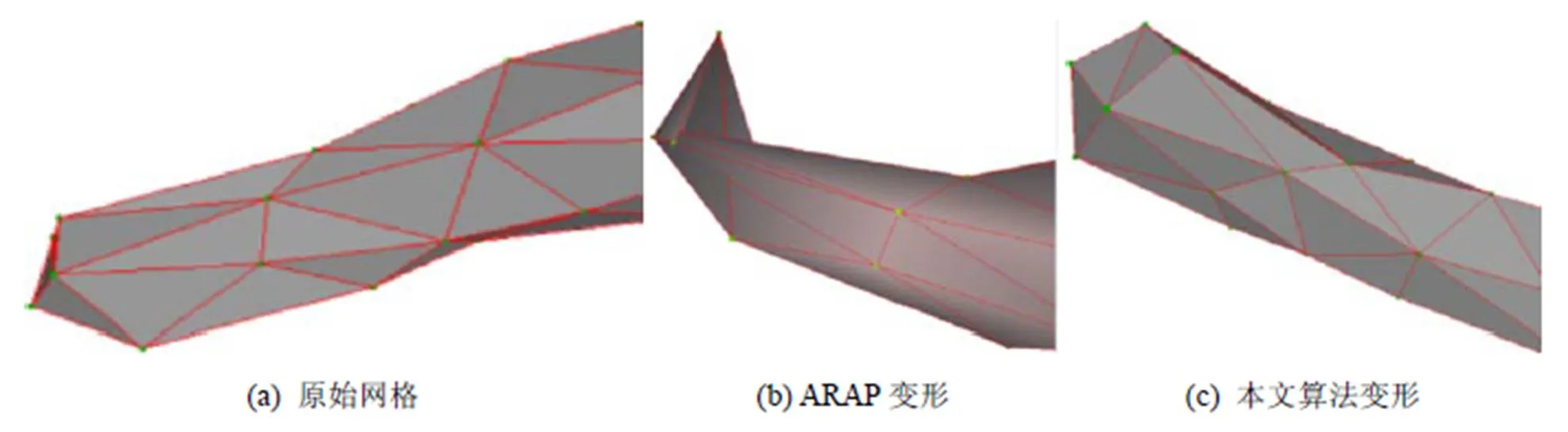
图8 Tyra尾部网格对比图

图9 Cactus变形对比图
在时间效率上,本文算法加入了计算测地场的步骤,但庆幸的是,计算测地场中多次所用的Laplacian算子在ARAP变形中已经计算得到,因此在一定程度上缩减了测地场计算所需的时间。在图形效果上,加入测地场约束能有效地避免大尺度以及非刚性变形所出现的畸变情况,通过测地场能量的约束,可加速图形的收敛速度。从表1可以看出,加入测地场优化所需要的时间仅为ARAP变形的1/3。
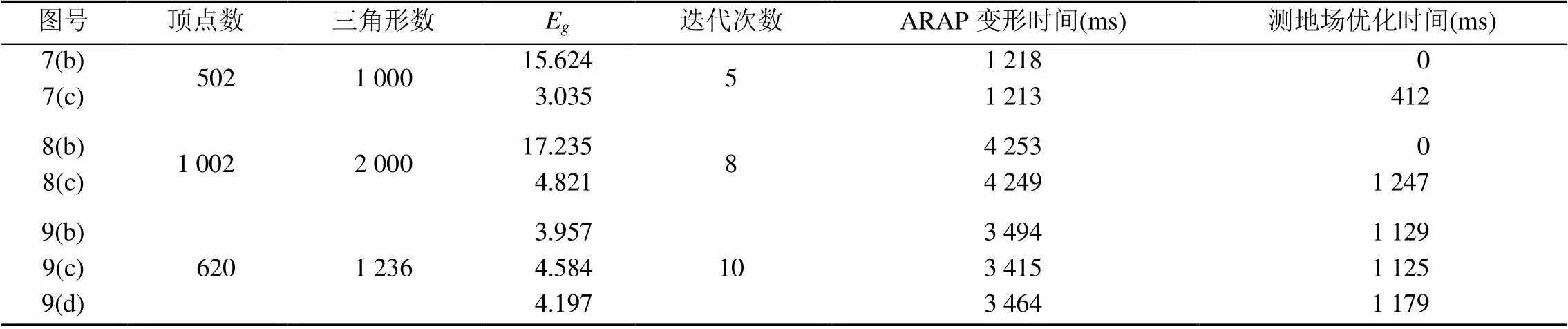
表1 本文算法运行时间
4 结束语
本文对ARAP变形技术进行拓展,加入了测地场优化这一步骤,改善了大尺度变形以及非刚性变形中出现的畸变,在保持ARAP变形技术的同时保持曲面细节,用测地场优化来实现宏观调控,加速了网格变形。以测地场能量来衡量网格变形优劣,避免了ARAP变形技术在非完全刚性变换时,能量函数在迭代过程中出现逆增长,而影响变形评价系统对变形完成程度的衡量。
本文算法的不足之处,当网格变形改变图形拓扑结构时,所提假设变形前后测地场变化较小将被否决;另并未将测地信息直接地加入到网格变形中,在今后的工作中需对其进行改进。
[1] YU Y Z, ZHOU K, XU D, et al. Mesh editing with poisson-based gradient field manipulation [C]//ACM SIGGRAPH. New York: ACM Press, 2004: 644-651.
[2] SORKINE O, COHEN-OR D, LIPMAN Y, et al. Laplacian surface editing [C]//In Proceeding of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing. New York: ACM Press, 2004: 175-184.
[3] SORKINE O, ALEXA M. As-rigid-as-possible surface modeling [C]//Proceedings of the 5th Eurographics Symposium on Geometry Processing. Aire-la-Ville: Eurographics Association Press, 2007: 109-116.
[4] ZHOU K, HUANG J, SNYDER J, et al. Large mesh deformation using the volumetric graph Laplacian [J]. ACM Transactions on Graphics, 2005, 24(3): 496-503.
[5] LIPMAN Y, SORKINE O, LEVIN D, et al. Linear rotation-invariant coordinates for meshes [J]. ACM Transactions on Graphics, 2005, 24(3): 479-487.
[6] SUESSMUTH J, ZOLLHÖFER M, SERT E, et al. GPU based ARAP deformation using volumetric lattices [C]// Eurographics 2012. Goslar: Eurographics Association Press, 2012: 85-88.
[7] LEVI Z, GOTSMAN C. Smooth rotation enhanced as-rigid-as-possible mesh animation [J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(2): 264-277.
[8] 杜正君, 张慧. 体积图控制的近似刚性的网格变形[J]. 计算机辅助设计与图形学学报, 2016, 28(2): 218-227.
[9] 刘炯宙, 李基拓, 陆国栋. 三维模型近刚性保体变形[J]. 计算机辅助设计与图形学学报, 2013, 25(4): 533-540.
[10] GAO L, ZHANG G X, LAI Y K. Lp, shape deformation [J]. Science China Information Sciences, 2012, 55(5): 983-993.
[11] CHAO I, PINKALL U, SANAN P, et al. A simple geometric model for elastic deformations [J]. ACM Transactions on Graphics, 2010, 29(4): 157-166.
[12] CHEN S Y, GAO L, LAI Y K, et al. Rigidity controllable as-rigid-as-possible shape deformation [J]. Graphical Models, 2017, 91: 13-21.
[13] AU K C, FU H, TAI C L, et al. Handle-aware isolines for scalable shape editing [J]. ACM Transactions on Graphics, 2007, 26(3): 83.1-83.10.
[14] CRANE K, WEISCHEDEL C, WARDETZKY M. Geodesics in heat: A new approach to computing distance based on heat flow [J]. ACM Transactions on Graphics, 2013, 32(5): 13-15.
As-Rigid-As-Possible Mesh Deformation Controlled by Geometric Field in Heat
SHAO Mao-zhen, SHOU Hua-hao
(College of Science, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China)
In order to maintain the details of the 3D model, correct the problem of distortion and folding of the as-rigid-as-possible (ARAP) mesh deformation used in large and nonperfect rigid deformation, an ARAP deformation method is proposed based on geometric field in heat. First, the Laplacian deformation of the model is carried out. On this basis, the rotation matrix of local cell is solved by singular value decomposition, and the rigid deformation energy of the model is calculated. Then by solving the sparse linear system, the deformation points are updated. By solving the two-time sparse linear system, we calculate the geometric field deviation of the deformation process, and correct the deformed mesh to get the deformation results close to those of the original mesh. Iterate the above steps until the geometric field deviation to meet certain requirements, and finally the final deformation results are obtained. The example shows that the method can quickly complete the mesh point correction function in mesh deformation process, and it can also effectively avoid grid collapse when applied to large-scale deformation.
as-rigid-as-possible mesh deformation; geometric field in heat; sparse linear system; folding
TP 391
10.11996/JG.j.2095-302X.2019010001
A
2095-302X(2019)01-0001-07
2018-06-26;
2018-07-13
国家自然科学基金项目(61572430)
邵茂真(1994-),男,浙江金华人,硕士研究生。主要研究方向为可视化计算。E-mail:434850246@qq.com
寿华好(1964-),男,浙江诸暨人,教授,博士,硕士生导师。主要研究方向为计算机辅助几何设计与图形学。E-mail:shh@zjut.edu.cn

