儿童数学抽象力形成的教学分析与提升策略

孙 欣 王乃涛

史宁中教授曾指出：人的基本思维能力就是想象能力和抽象能力，其他思维能力都是它们派生的。数学抽象最能体现数学本质。

一、儿童数学抽象力形成的困惑

（一）对原初概念表征不清，抽象过程缺少思维基础

我们通常用已知概念（原初概念）来定义新概念，如用因数来定义质数、合数，用自然数来定义因数。学生对原初概念的理解直接影响他们的新概念形成。如学习苏教版四下《三角形的高》一课时，由于学生对原初概念的表征与理解不清，往往会致使其新概念抽象过程模糊（如表1）。

（二）对问题解决机械模仿，抽象方法选择运用不当

教师常结合生活情境来帮助学生理解数学问题，以培养他们用数学的眼光观察生活的能力。但是，如果教学浮于表面，学生则会对方法理解不透、运用不当。如学习苏教版一下《100以内加减法》一课时，常常会出现如下页表2所示的问题。两道题题型相同，正确率却相差较大。题1找回钱数很少，符合生活中找回钱少的现实暗示，学生会根据数据特点机械模仿解决题1的方法来解决题2。

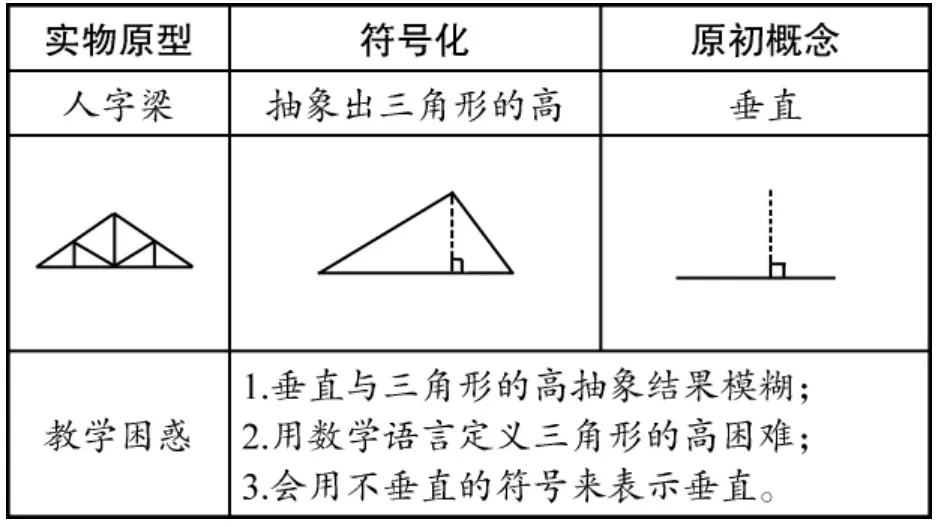
表1 对原初概念表征不清示例

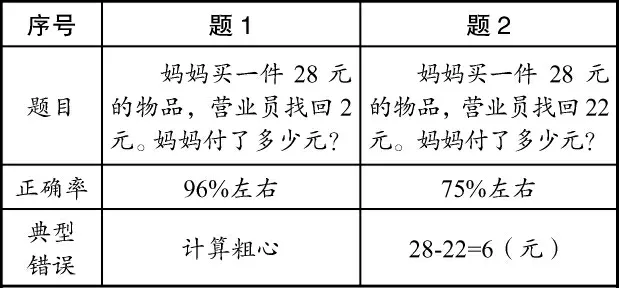
表2 对问题解决机械模仿示例

（三）对数学原理表达不清，抽象结论难以语义说明

学数学需探究数学原理。建构数学原理时，可举例、归纳、概括，也可以纯数学逻辑推导。受认知能力限制，学生表达数学原理时往往会出现不全面、不完整、不准确等情况。如教学苏教版五下《分数的基本性质》一课，在折纸、填等式、发现分子分母倍数关系等环节，学生能轻松应对，但让他们用语言概括规律时，他们的表达却往往不如人意，有的只表达出了乘或除中的一种情况，有的考虑不到0除外。

（四）对数学本质把握不准，核心要素难以深刻辨析

同一对象可用不同标准进行分类。同一概念处于不同上位概念之下，也以不同树状结构引发下位概念。学生对交叉状的概念体系结构往往难以辨别。如教学苏教版五下《因数与倍数》一课，不等于0的自然数可分为1、质数和合数，也可分为奇数和偶数。但因学生对数学概念的核心要素把握不准，导致他们对两种分类标准（是否2的倍数，因数有多少）和概念结构难以深入辨析。

二、儿童数学抽象力的含义及学习特征

（一）儿童数学抽象力的含义

数学抽象力是在数学抽象过程中形成的理解力、判断力、想象力、概括力等能力的总和。

（二）儿童数学抽象学习的典型特征

小学生的数学抽象主要指情境性抽象或经验性抽象，具有两重性，既表示从情境中提取的过程，又表示从过程中得出的经验概念。

1.表达的直接性。儿童头脑中的信息属于“自然结构”，加工起来相对困难，难以进行数学逻辑解释，而是一点一点地直接表达想法。

2.表征的直观性。儿童表征数学概念从实物、图形开始，尚不能完全脱离数学原型展开逻辑思考，抽象过程以具体形象和表象为支撑。

3.原理的探究性。儿童不满足于接受现有的结论，喜欢从数学事实出发猜想、追问、寻找数学规律，具有一定的探究意识与能力。

4.思维的半逻辑性。儿童抽象能力的发展介于实物、图形的形象认知和原理、规律的抽象过程之间，具有一定的但不完全的逻辑性，我们

称为“半逻辑性”的学习特点。

三、儿童数学抽象力的培养策略

（一）全面打破——匹配抽象内容的适应场

数学抽象主要有概念抽象、规律抽象、运算抽象、关系抽象、思想方法抽象等。

1.概念抽象——去异求同，抽离本质属性。要促进学生建立数学概念，教师应注重引导学生观察、比较，区别事物的本质属性与非本质属性，发现事物间共同的属性，形成正确的概念。如教学苏教版二下《认识角》一课，可出示实物图片，引导学生描出图片中的角，从实物图中剥离出角的平面图形，再通过观察、比较抽象出平面图形的共同特点，抽离出角的本质属性（由一个顶点和两条边组成）。

2.规律抽象——去粗取精，概括临近结论。在规律探究中，学生根据研究素材形成的发现有些无普适性。教师应引导学生去除外在表象，展示本质，在临近结论的基础上形成正确的结论。如教学苏教版四下《多边形内角和》一课，学生通过量、算、拼等方法得出了三角形与四边形的内角和及2倍关系，但还不能发现边数与内角和的关系。教师适时启发：想象一下，多边形的内角和会与什么有关？当学生理解了多边形内角和与三角形内角和有关时，就容易找到研究五、六边形内角和的方法了。借助图形直观进行归纳推理，解释规律的合理性，有助于学生矫正其临近结论。

3.运算抽象——理法相通，提炼运算法则。在计算教学中，沟通算理与算法很重要。算理是算法的基础，及时沟通算法与算理的联系有利于算法的抽象、提炼与掌握。如苏教版三下《两位数乘两位数的笔算》一课的例题为：幼儿园购进12箱迷你南瓜，每箱24个。一共有多少个？教师教学时应注意引导学生理解算理和竖式过程（如图1），沟通新旧方法，并启发学生讨论：（1）竖式中第二步算出的积的末位为什么要与十位对齐？（2）新算法为什么要分步表示过程？在数学问题情境中沟通新旧方法，理解算理，抽象出运算法则。

图1 例题解决过程

4.关系抽象——先主后次，多角度确定解题思路。关系抽象包含数量关系、图形关系等的抽象，数、形、量之间有着密切的关联。教师应注重引导学生打破各种关系的界限，使他们形成有主次、多角度解决问题的意识。如教学苏教版六下《按比例分配》一课，解决“甲数是48，甲数、乙数的比是6∶5，求甲数、乙数的和”这道题时，把6∶5看作份数，可列出48÷6×5+48这样的算式；把6∶5看作分数，可列出48÷6×5+48、48÷+48这样的算式。将不同类型的关系进行融通，打破割裂、单一、凝固的教学格局，有助于拓宽学生的解题视野，促进他们抓住问题关键抽象出解题模型。

（二）全向打通——激活抽象方法的运用场

抽象过程中会用到多种数学思想方法，主要有分类与比较、归纳与概括、推理与想象等。

1.分类与比较——抓共同点，彰显同一性。分类大致有分情况讨论和概念分类两种情况。如教学苏教版三上《认识几分之一》一课时，可出示一些图形，有平均分成2份、3份、4份的，有不平均分成2份、3份、4份的，然后组织学生经历两级、两种分类比较（如图2），并引导他们发现：先按相等份数或是否平均分分类，分类结果相同，说明每类具有相同的属性。渗透分类比较思想，促进学生发现每类图形的本质，能为他们抽象出分数的本质属性打下基础，为他们正确认识分数的意义打开通道。

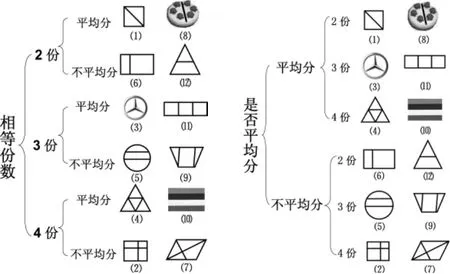
图2 一些图形的两级、两种分类比较

2.归纳与概括——抓表达，强调正确性。抽象和概括存在于同一母体，一同发生、发展。概括出的概念是建立新概念的基础，可推广到该类对象中。如数“5”是从5个人、5只鸟、5幢楼等事物中舍去非本质特征，概括出本质特征——数量相等而抽象出来的。此方法可用来表示基本“数符号”，但要注意表达的正确性。

3.推理与想象——抓逻辑，体现合理性。抽象过程离不开想象，是指根据数学对象表面相似或本质的联系展开形式到形式或内在到内在的联想。如教学苏教版五上《小数的意义》一课，可借助米尺使学生直观地认识一位（两位）小数表示十分之几（百分之几），引导他们联想到三位小数表示千分之几，并追问：我们需要把1000份全部画出来吗？进而适时点拨：数学学习未必需要把所有情况都呈现出来，推理、想象同样能帮助我们得到结果。通过推理与想象抽象出数学的本质属性，有助于学生抓住数学的内在逻辑，感受抽象结论的合理性。

（三）全息递进——提升高阶思维的层次场

儿童数学抽象思维的层次应匹配数学对象抽象的层次。如自然数抽象比代数式抽象更具体，故理解代数式所需的抽象力高于理解自然数所需的抽象力。

1.实物层面的抽象——从现实情境剥离出数学问题。实物层面的抽象是基于已有生活经验与生活现实的抽象，以实物为抽取对象，到超越实物而尚未完全脱离实物结束。如教学苏教版三上《平移与旋转》一课，教师首先呈现升降国旗图、火车行驶图、吊扇图、钟表图等，瞬间把学生带入平移（旋转）的情境，让他们感受平移（旋转）的运动特点，思考图形怎样运动可以称为平移（旋转）。借助实物从适合的现实情境剥离出数学问题，有助于学生把握事物的内在属性。

2.半符号层面的抽象——把数学问题转化为儿童经验。半符号抽象是实物抽象基础上的发展。如教学苏教版三上《轴对称图形》一课，在学生初识轴对称图形的概念后，可呈现形态各异的图形，如交通标志、字母等，组织学生找出其中的轴对称图形。然后引导他们运用对折后两边完全重合这一关键属性深化轴对称图形的概念，这是实物直观层面的第二次抽象，处于半符号层面，此时，数学问题已经转化为儿童的抽象经验了。

3.符号层面的抽象——把儿童经验浓缩为概念原理。符号层面的抽象具有典型的阶段性、层次性，抽象形式已去掉具体内容，可用概念、符号、关系等表述已简约化的单个事物或一类事物。如教学苏教版五下《分数的意义》一课时，教师引导学生回顾平均分蛋糕、长方形、一米长度、一些物体后，揭示一个物体、一个图形、一个计量单位、一个整体都叫单位“1”，然后让学生根据一（几）幅图中的某个分数的具体意义抽象概括分数的一般意义，扩大分数意义的内涵和外延，完成符号层面的抽象。引导学生抓住数学概念、原理的共同特征，用概括、抽象、简洁的数学符号表达出来，有助于他们深入理解数学概念或数学原理。

4.形式化层面的抽象——把数学原理输出为数学模型。形式化层面的抽象处于数学抽象的普适阶段，它通过假设和推理建立法则、模式或模型，并在一般意义上解释具体事物。如基于对比例概念的认识，学生可建立新的数学原理。如学习“解比例”时，可引导学生通过解决“在电脑上把长6厘米、宽4厘米的照片按比例放大，放大后照片的长是13.5厘米，宽是多少厘米？”这样的问题，把模型运用到问题解决中。引导学生从数学现实中概括、抽象出数量关系和解题规律，通过形式化抽象处理，能有效提升学生的数学抽象力。

总之，数学抽象力是儿童数学学习的必备品质，教师教学时应注重建构有助于提升儿童数学抽象力的适性场域。