概率统计核心考点测试卷B

■河南省项城市第一高级中学 赵学斌

一、选择题

1.二胎政策的放开使得家庭中有两个小孩的现象普遍存在,某单位关系要好的甲、乙、丙、丁四个家庭各有两个小孩共8人,准备使用某打车软件,分乘A、B两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中甲户家庭的孪生姐妹需乘同一辆车,则乘坐A车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )。

A.48种 B.36种

C.24种 D.18种

A.4 B.6 C.10 D.12

3.一个箱子里有编号为1,2,…,12的12个大小相同的球,其中1～6号球是黑球,其余的是白球,若从中任取两个球,则取到的都是黑球,且有偶数编号球的概率为( )。

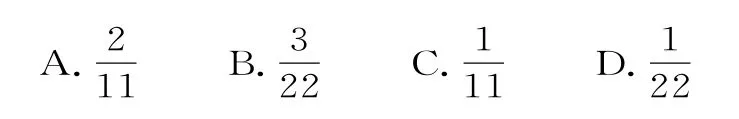
4.某种品牌照明灯的使用寿命(单位:年)服从正态分布,且使用寿命不少于2年的概率为0.8,使用寿命不少于6年的概率为0.2。河南省某中学在宿舍门口同时安装了两个该种品牌的照明灯,则在4年内这两个照明灯都能正常工作的概率为( )。

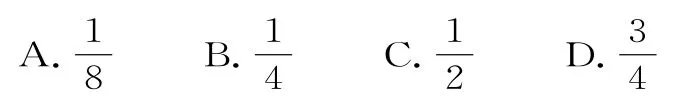
5.一次掷两颗骰子,设两颗骰子得到的点数分别为m,n,则直线与圆(x-3)2+y2=1相交的概率是( )。6.如图1所示,在圆心角为的扇形A O B中,以圆心O为起点作射线O C,O D,则使

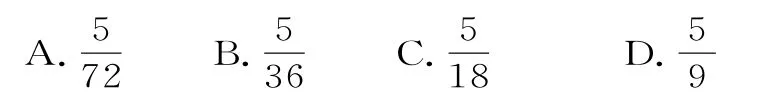
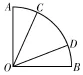
图1

7.一台机器生产某种产品,如果生产一件甲等品可获利50元,生产一件乙等品可获利30元,生产一件次品,要赔20元,已知这台机器生产甲等品、乙等品和次品的概率分别为0.6、0.3和0.1,则这台机器每生产一件产品,平均预期可获利( )。

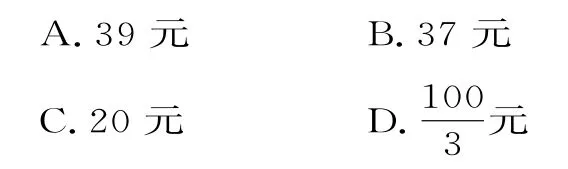
8.在4次独立重复试验中,随机事件A恰好发生2次的概率不大于其恰好发生1次的概率,则事件A在1次试验中发生的概率P的范围是( )。

A.(0,0.6] B.[0.6,1)

C.(0,0.4] D.[0.4,1)

9.设 X～N(μ,σ2),其正态分布密度曲线如图2所示,且P(X≥3)=0.0228,那么向正方形O A B C中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )。

图2

(已知若X～N(μ,σ2),则P(μ-σ＜

10.为了解某社区居民有无收看“春节联欢晚会”,某记者分别从某社区60～70岁40～50岁,20～30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人,若在60～70岁这个年龄段中抽查了8人,那么x为( )。

A.90 B.120 C.180 D.200

11.为了提高当地居民的生活质量,某市政府推出了一系列惠民政策。为了解百姓对政府政策的满意度,从甲、乙两地区分别随机调查了100户居民,根据满意度评分,分别得到甲地区和乙地区居民满意度评分的频率分布直方图,如图3所示。若甲地区和乙地区居民满意度评分的中位数分别为z1,z2,平均数分别为p1,p2,则下面正确的是( )。

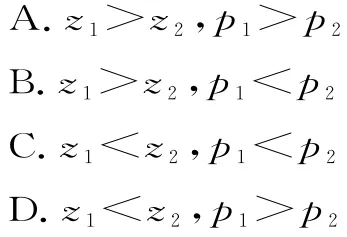
图3

12.下列命题中:

②在回归分析中,相关指数R2为0.80的模型比相关指数R2为0.98的模型拟合的效果要好;

其中真命题的个数是( )。

A.1 B.2 C.3 D.4

二、填空题

13.某学校食堂早餐有小米粥、大米粥、绿豆粥和胡辣汤四种食物可供食用,有5名同学前去就餐,每人只选择其中一种,且每种食物都至少有一名同学选择。已知大米粥剩余的仅够一人食用,甲同学肠胃不好不会选择胡辣汤,则这5名同学不同的食物选择方案种数为____。(用数字作答)

14.在区间[-1,1]上任取两数m和n,则关于x的方程x2+m x+n2=0有两个不相等实根的概率为____。

15.设随机变量X的概率分布如表1所示,且随机变量X的均值E(X)为,则随机变量X的方差D(X)为____。

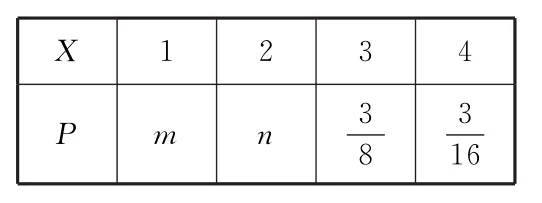
表1

16.已知由样本数据点(xi,yi)(i=1,2,3,…,n),求得的回归直线方程为^y=1.2 3x+0.数点,且=4,若去掉两个数据点(4.1,5.7)和(3.9,4.3)后重新求得的回归直线l的斜率估计值为1.2,则此回归直线l的方程为____。

三、解答题

17.某刀片厂生产某型号刀片每盒12片,每批生产若干盒,每片成本1元,每盒刀片需检验合格后方可出厂。检验方案是从每盒刀片中随机取3片检验,若发现次品,就要把全盒12片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒刀片合格,不再检验,可出厂。

(1)若某盒刀片中有9片合格,3片不合格,求该盒刀片经一次检验即可出厂的概率。

(2)设每片刀片不合格的概率为p(0＜p＜1),且相互独立。若某盒12片刀片中恰有3片次品的概率为f(p),求f(p)的最大值及取得最大值时p的值。

18.已知f(x)=x-1,g(x)=|x|。

(1)若x是从区间[-3,4]上任取的一个实数,y=2,求满足g(x)≥|f(y)+1|的概率。

(2)若x,y都是从区间[0,4]上任取的一个实数,求满足(f(y)+1)2+g2(x)≤4的概率。

19.某学校为高三学生提供数学学科和物理学科高考二轮备考专题讲座,以提高高三学生备考的效率。每名高三学生可以选择参加一科讲座、参加两科讲座或不参加讲座。已知参加物理学科的有60%,参加数学学科的有75%,假设每个人对学科讲座的选择是相互独立的,且每个人的选择相互之间没有影响。

(1)任选1名高三学生,求该学生参加专题讲座的概率;

(2)任选3名高三学生,记ξ为3人中参加专题讲座的人数,求ξ的分布列。

20.经济的快速发展使我们的生活质量发生了翻天覆地的变化,同时随着工业化及城市车辆的增加,城市的空气污染越来越严重,空气质量指数A P I一直居高不下,对人体的呼吸系统造成了严重的影响。某市卫生局调查了本地500名居民的工作场所和呼吸系统健康情况,得到2×2列联表,如表2:

表2

(1)补全2×2列联表。

(2)是否有95%的把握认为感染呼吸系统疾病与工作场所有关?

(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机地抽取两人,求两人都有呼吸系统疾病的概率。

附参考公式与临界值表(表3):K2=,

其中n=a+

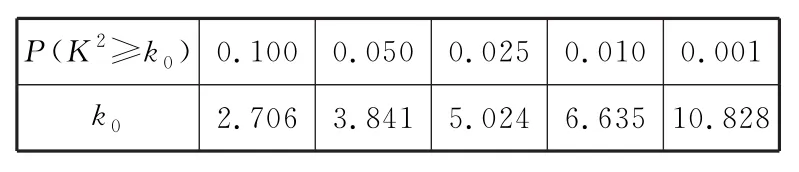
表3

21.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数如表4所示。

该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求回归方程,再用被选取的2组数据进行检验。

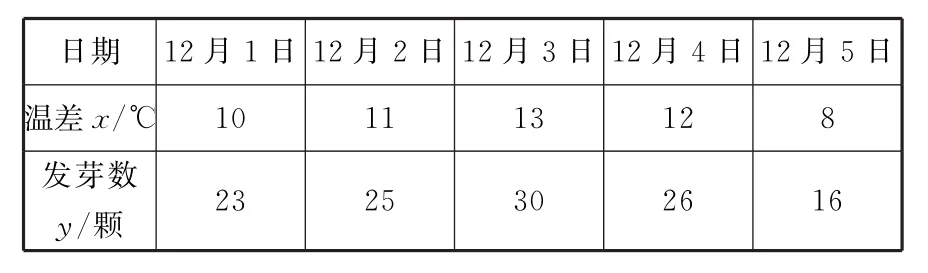
表4

(1)求选取的2组数据恰好是不相邻的2组数据的概率。

(2)若选取的是12月1日与12月5日的2组数据,请根据12月2日至12月4日的数据,求y关于x的线性回归方程^y=

(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?

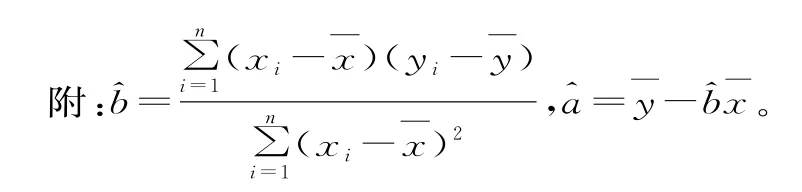
图4

(1)如果成绩大于135分的为特别优秀,求本次考试英语、数学特别优秀的大约各多少人。

(2)试问:本次考试英语和数学的成绩哪个较高?并说明理由。

(3)若从1000名高三学生中随机抽取500名,然后再把这500名学生中英语特别优秀、数学特别优秀的都抽出来作为一个样本,如果从该样本中随机抽取3人(该样本中英语和数学两科都特别优秀的共有6人),设抽取的3人中两科都特别优秀的有ξ人,求ξ的分布列和数学期望。

附参考公式及数据:若X～N(μ,σ2),则P(μ-σ＜X≤μ+σ)=0.68,P(μ-2σ＜X≤μ+2σ)=0.96,P(μ-3σ＜X≤μ+3σ)=0.99。