兵马未动，建系先行——谈如何建立空间直角坐标系

■浙江省绍兴市上虞区职教中心综高部 章成尧

空间向量的引入为应用代数方法处理立体几何问题提供了一种重要的工具和方法。而通过建立空间直角坐标系,借助空间向量坐标运算来计算和证明立体几何问题,用定量的计算代替定性的分析,从而可避免一些烦琐的推理论证,大大简化思维过程与运算。本文例析如何利用向量解题的关键步骤,即如何建立恰当的坐标系。

一、直接建系

当图形中有明显互相垂直且相交于一点的三条直线时,可以利用这三条直线直接建系,一般地,竖起方向的直线为z轴,x,y,z轴逆时针方向设置。

例1如图1,棱长为3的正方体的顶点A在平面α上,三条棱A B,A C,A D都在平面α的同侧,若顶点B,C到平面α的距离分别为1,2,则顶点D到平面α的距离是___。

图1

分析:本题条件正规,但位置不正规。涉及的知识虽然只有线面距离和线面角,但难以下手。出路何在?考虑到正方体这一模型的特殊性,直接建立“倾斜”的空间直角坐标系,可达到柳暗花明又一村的效果。

解:以A为坐标原点,射线A C为x轴的正半轴,射线A B为y轴的正半轴,射线A D为z轴的正半轴建立空间直角坐标系A-x y z。则A(0,0,0),B(0,3,0),C(3,0,0),D(0,0,3)。设平面α的法向量为n=(x,y,1),则由题可知

点评:一般地,如果多面体的棱之间具有明显的垂直关系(如正四棱柱等),则可以直接建立坐标系。当然,为计算方便,最好建立恰当坐标系,如避免出坐标负值等。

二、通过平面几何图形画出x或y轴来建系

许多立体几何问题的建系不是一蹴而就的,如待建的x或y轴不明显,此时就需要我们通过分析平面几何图形的特性(因为一般地,x或y轴落在同一个平面图形中),挖掘平面图形中的垂直关系,画出相应的、恰当的x或y轴,达到建系的目的。

例2(2 0 1 8年浙江省高考试题)如图2,已知多面体A B C A1B1C1,A1A,B1B,C1C均垂直于平面A B C,∠A B C=1 2 0°,A1A=4,C1C=1,A B=B C=B1B=2。

(Ⅰ)证明:A B1⊥ 平面A1B1C1;

(Ⅱ)求直线A C1与平面A B B1所成的角的正弦值。

分析:若以点A、B、C其中之一为坐标原点,则x,y,z轴不能明确,其他点坐标也不

能轻松表示。当把A C的中点O作为坐标原点时,依据等腰三角形的性质容易确定三坐标轴,有用点的坐标也更易于操作了。

解:(Ⅰ)如图3,以A C的中点O为原点,分别以射线O B,O C为x,y轴的正半轴,建立空间直角坐标系O-x y z。

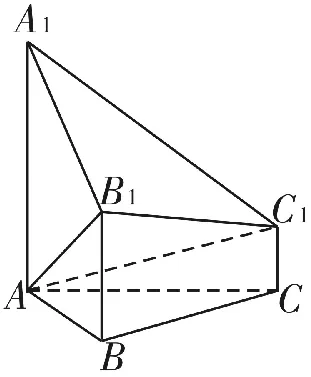
图2

由题意知各点坐标如下:

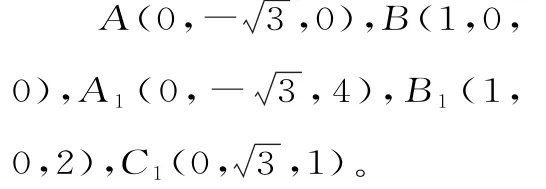
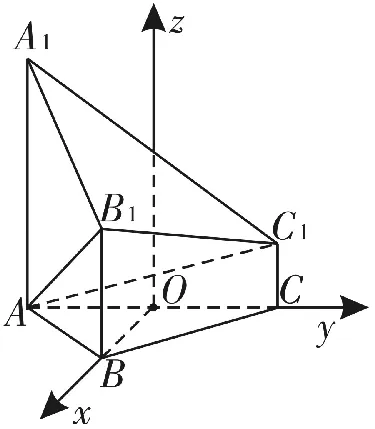
图3

所以A B1⊥平面A1B1C1。

(Ⅱ)设直线A C1与平面A B B1所成的角为θ。

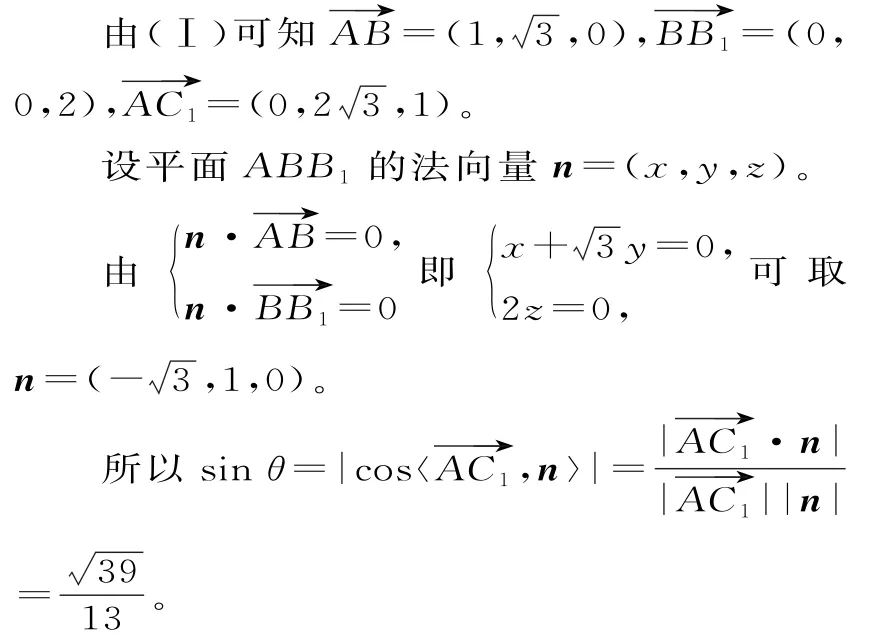
因此,直线A C1与平面A B B1所成的角的正弦值是

点评:将逻辑推理算法化是向量法的本质。本题把证明线线垂直问题转化为向量数量积为0的运算,体现了数学的转化思想,也凸显了坐标系选择的重要性。

三、利用面面垂直画出z轴来建系

在建系过程中,z轴是“顶梁柱”,是事关建系成败的中流砥柱。因此,许多试题在命题时常从z轴入手,设置需要人为画出z轴的试题。根据z轴的特征(垂直于底面)这一线面垂直关系,可以通过面面垂直来作,以达到建系的目的。

图4

例3 (2 0 1 1年重庆高考试题)如图4,在四面体A B C D中,平面A B C⊥平面A C D,A B⊥B C,A D=C D,∠C A D=3 0°。若二面角C-A B-D为6 0°,求异面直线A D与B C所成角的余弦值。

分析:搭房先“竖梁”,本题建系的突破口是如何作出z轴,可从“平面A B C⊥平面A C D”这一条件入手。

解:如图5,过A C中点F作FM⊥A C,交A B于M,已知A D=C D,平面A B C⊥平面A C D,易知F C,F D,FM两两垂直,以F为原点,射线FM,F C,F D分别为x轴,y轴,z轴的正半轴,建立空间直角坐标系F-x y z。

图5

不妨设A D=2,由C D=A D,∠C A D=3 0°,易知点A,C,D的坐标分别为A(0,D(0,0,1),则(0,3,1)。

显然向量k=(0,0,1)是平面A B C的法向量。

已知二面角C-A B-D为6 0°,故可取平面A B D的单位法向量j=(l,m,n),使得

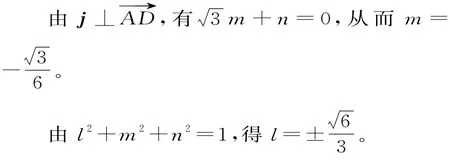
点评:面面垂直常转化为线面垂直,而这根线将是所建的坐标系中的重要“竖梁”。

四、利用图形的对称性建系

图形中没有明显交于一点的三条直线,但图形中有一定对称关系(如正三棱柱、正四棱柱等)时可利用图形对称性建立空间直角坐标系解题。

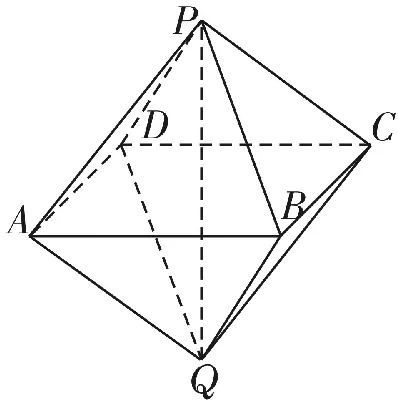
图6

例4如图6,已知两个正四棱锥P-A B C D与Q-A B C D的高都是2,A B=4。

(1)证明P Q⊥平面A B C D;

(2)求异面直线A Q与P B所成的角;

(3)求点P到平面Q A D的距离。

分析:解决问题(1)显然是建系的关键,该几何体具有明显的对称关系,而对称关系同时蕴含着垂直关系,为建系提供“画”点。

解:(1)连接A C、B D,设A C∩B D=O。

由于P-A B C D与Q-A B C D都是正四棱锥,所以P O⊥平面A B C D,Q O⊥平面A B C D。

从而P、O、Q三点在一条直线上,所以P Q⊥平面A B C D。

(2)由题设知,A B C D是正方形,所以A C⊥B D。

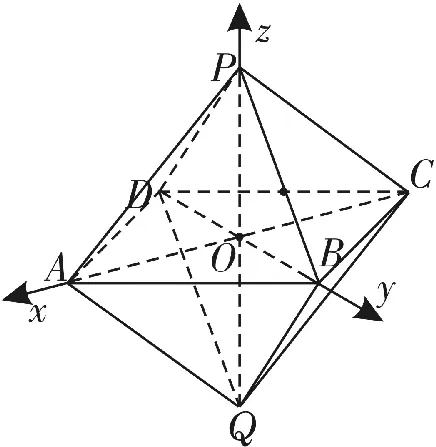
由(1)知,Q O⊥平面A B C D。

故可分别以直线C A、D B、Q P为x轴、y轴、z轴建立空间直角坐标系(如图7)。由题给条件,相关各点的坐标分别是P(0,0,2),A(2 2,0,0),Q(0,0,-2),B(0,2 2,0)。

点评:两个正四棱锥高相等,故可利用其对称性建立空间直角坐标系。