六法巧突破，妙解线面角——谈2 0 1 8年浙江第1 9题解法

■江苏省张家港中等专业学校 韩文美

立体几何中的空间角,能比较集中地考查同学们的空间想象能力、推理论证能力与运算求解能力,历来被高考命题者青睐,几乎年年必考,只是改变问题背景与设问角度而已。直线与平面所成的角求解方法往往比较多,可以通过几何法、坐标法、向量法、等积法等来处理,根据不同题目背景选择恰当的方法来解决即可。

【高考真题】(2 0 1 8年浙江第1 9题)如图1,已知多面体A B C A1B1C1,A1A,B1B,C1C均垂直于平面A B C,∠A B C=1 2 0°,A1A=4,C1C=1,A B=B C=B1B=2。

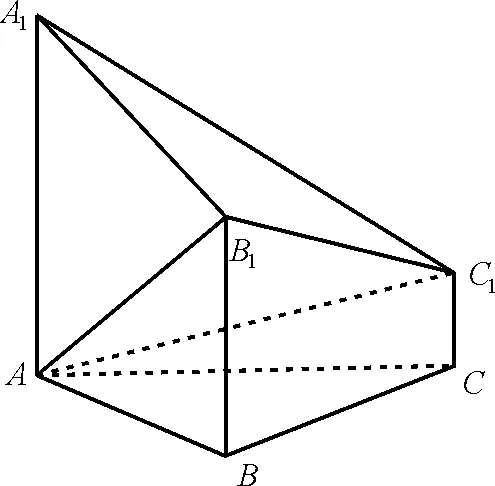
图1

(1)证明:A B1⊥平面A1B1C1;

(2)求直线A C1与平面A B B1所成的角的正弦值。

解法1(几何法):(1)因为A1A⊥平面A B C,B1B⊥平面A B C,所以

因为A A1=4,B B1=2,A B=2,所以

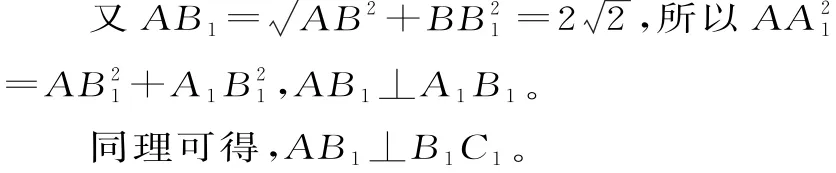
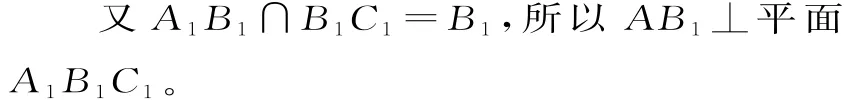
(2)如图2所示,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接A D。

因为A B1⊥平面A1B1C1,所以平面A B B1⊥平面A1B1C1。

图2

又C1D⊥A1B1,所以C1D⊥平面A B B1,∠C1A D就是直线A C1与平面A B B1所成的角。

由∠A B C=1 2 0°,A B=B C=2,由余弦定理可得A C=2 3,解得A C1=1 3。

所以C1D=A1C1·

因此,直线A C1与平面A B B1所成的角的正弦值是

解法2(坐标法):(1)如图3,以A C的中点O为原点,分别以射线O B,O C为x轴,y轴的正半轴,建立空间直角坐标系O-x y z。

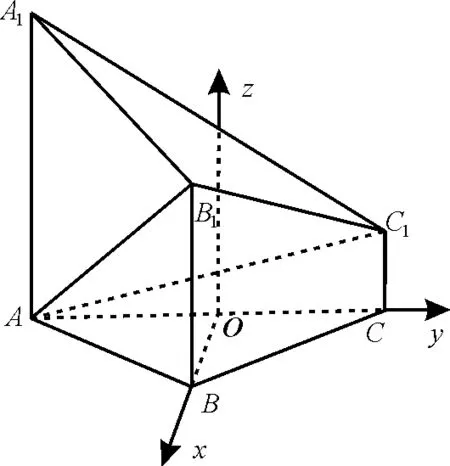
图3

因此,直线A C1与平面A B B1所成的角的正弦值为

解法3(几何法的改进法):(1)同解法1。

(2)如图4,过点C作A B的延长线的垂线C D,垂足为D。由B1B,C1C均垂直于平面A B C,可得B1B∥C1C,所以C1C∥平面A B B1。

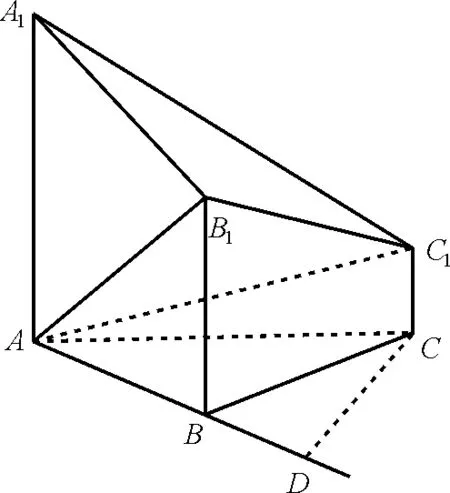
图4

所以点C1到平面A B B1的距离与点C到平面A B B1的距离相等,可得d=C D=B C·s i n6 0°=。

∠A B C=1 2 0°,A B=B C=2,由余弦定理可得A C=,解得

设直线A C1与平面A B B1所成的角为θ,则有s i n

因此,直线A C1与平面A B B1所成的角

解法4(基底法):(1)同解法1。

(2)由∠A B C=1 2 0°,A B=B C=2,由余弦定理可得A C=2 3。

设平面A B B1的法向量为n=x a+y b+

解法5(向量法):(1)同解法1。

(2)过点C作A B的延长线的垂线C D,垂足为D,则C D⊥平面是平面A B B1的法向量。

此类立体几何问题是近年高考中比较基础的一类题型,题目不难,入口宽,方法多,正确分析图形的特征对理解与解决问题很有帮助,同时高中阶段的相关的学习方法几乎都可以用上,给了每一位同学相同的成功机会。无论采用哪种方法来解决相应的直线与平面所成的角问题,都充分考查了同学们各方面的能力。其实,进一步转化思维,把对应的空间图形补成与之对应的直三棱柱或四棱锥,也是一个非常不错的思维方向。