正则化的近似最大公因子的图像盲复原算法
张万磊,杨阳,冯涛,李喆
(1.长春理工大学 电子信息工程学院,长春 130022;2.长春理工大学 理学院,长春 130022)
在线性不变的空间中,退化图像的复原是一个求逆的过程。根据相关的点扩散函数(简称PSF)的先验知识是否已知,将退化图像的复原分为退化图像的盲复原和退化图像的非盲复原[1]。非盲复原就是在退化图像相关的先验知识已知的情况下,进行解卷积运算。而图像盲复原就是在PSF未知的情况下,利用盲复原算法实现退化图像的清晰化。图像的退化模型如图1所示。可以用下面的数学表达式来描述退化过程:
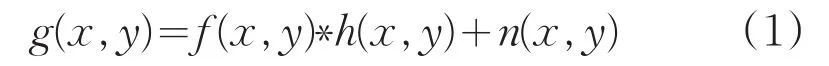
式中,g(x,y)代表退化图像,f(x,y)代表原始图像,h(x,y)代表图像退化过程中的PSF,n(x,y)代表获取图像过程中叠加的噪声,“*”代表卷积运算。
由于在盲复原过程中缺少一些先验信息,退化图像中又存在噪声,这使得图像的盲复原不再是一个简单的逆滤波过程。1997年,Liang和Pillai[2]提出了近似最大公因子图像盲复原算法,该算法把原始图像看成多幅退化图像的GCD,将二维GCD问题转化为一维Sylvester型GCD算法,进而实现图像盲复原。2010年,支丽红等人[3]提出了快速近似GCD图像盲复原算法,降低了盲复原算法的计算量。2015年,Belhaj等人[4]提出了基于Hankel矩阵计算GCD的图像盲复原算法,将单变量GCD算法运用在连续变换矩阵为上三角Toeplitz矩阵中。2017年,Toca等人[5]提出了基于Bezout矩阵的图像盲复原算法,该算法使用Barnett方法的广义Bezout矩阵来求解GCD。
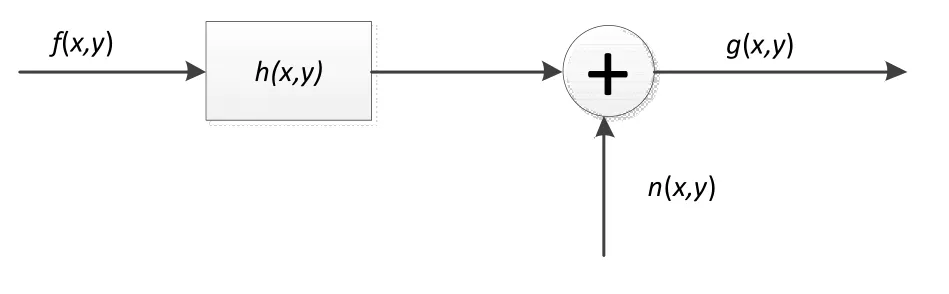
图1 图像的退化模型
该盲复原算法在估计出点扩散函数之后,直接进行反卷积,表达式如下:
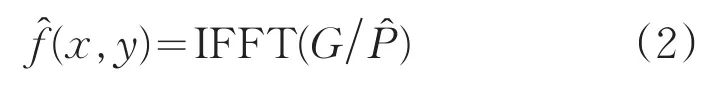
即直接逆滤波的算法,其中IFFT表示逆快速傅立叶变换,G代表退化图像的傅立叶变换,代表估计的PSF的傅立叶变换,(x,y)代表复原的图像。在平面上有些区域上为零或者非常小,F上相应区域的数值会剧烈地变化,这些区域的噪声会被放大,产生较大的偏差。其次,该算法缺乏约束条件,不能有效抑制因噪声扰动和数值计算产生的误差,误差会不断累积并向下传递。以上这些因素都会影响复原图像的质量。针对上面的问题,本文提出了相关的改进算法,从抑制噪声和反卷积运算约束两个方面去改进近似GCD图像盲复原算法,提高算法的鲁棒性。
1 近似GCD图像盲复原算法
定义1.二维Z变换将m×n矩阵P的元素映射到双变量多项式p(x,y)的系数[3]:

其中,x=[1,x,x2,...,xm-1]T,y=[1,y,y2,...,yn-1]T。根据上面的定义可以把式(1)变换成:
式中,G,F,H,N分别代表g(x,y),f(x,y),h(x,y),n(x,y)的二维Z变换。
假设原图像为f(x,y),两个退化图像为g1(x,y),g2(x,y)。两者的PSF分别为h1(x,y),h2(x,y),加性噪声分别为n1(x,y),n2(x,y),把g1(x,y),
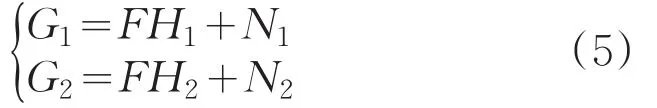
通常来说deg(H1)和deg(H2)与deg(F)相比非常小,(其中deg为多项式中各个变量的最高次数),两者的近似GCD的支撑区域较大,可以通过计算多项式G1,G2的近似GCD实现图像盲复原。对于退化的RGB图像,可以对R、G、B三个通道分别描述,如下所示:g2(x,y)进行二维Z变换得到下面的表达式:

1.1 单变量多项式近似GCD算法
假设给出两个单变量多项式f1,f2∈C[x]{0},deg(f1)=m和deg(f2)=n,m≥n,


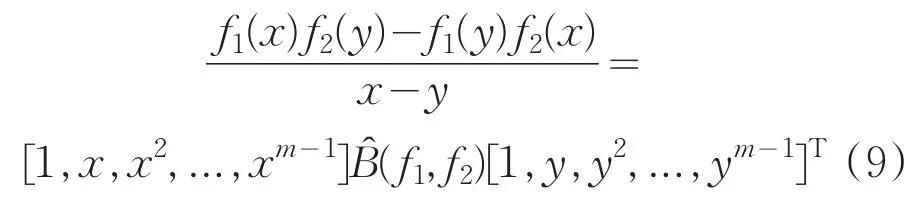
其中,Bezout矩阵定义如下:

式中,J是单位反对角矩阵。
定理1.给定单变量多项式f1,f2∈C[x],其中deg(f1)=m,deg(f2)=n,m≥n,那么有如下结论:

其中,dim代表矩阵的维度,NullSpace代表矩阵的零空间[6]。
定理2.给定单变量多项式f1(x),f2(x),deg(f1)=m,deg(f2)=n,m≥n。令p(x)=gcd(f1,f2)与deg(p)=r,结论如下所示:
(1)对于k≤m-r,rank(B(f1,f2))=m-r和det(B(f1,f2)k),其中B(f1,f2)k是B(f1,f2)的子矩阵,但对于k>m-r,det(B(f1,f2)k)=0。
(2)假设y=[1,y,y2,...,ym-1]T满足Cy=b,其中C=B(f1,f2)m-r,-b是由矩阵B(f1,f2)的第m-r+1个列向量的前m-r列构成。使:
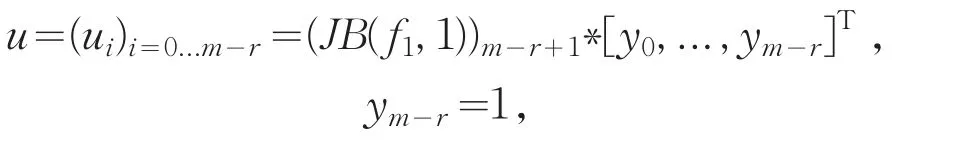
则f1(x)=p(x)u(x),其中。
根据定理2,可以通过检查前1×1,2×2,4×4,...,2[log2(m-r+1)]×2[log2(m-r+1)]子矩阵是否是奇异矩阵,从而有效地估计gcd(f1,f2)的次数r。假设r=deg(gcd(f1,f2)),可以通过求解 (m-r)×(m-r)线性系统来计算辅因子u(x),同时使用基于快速傅立叶变换的近似多项式除法来计算出GCD。显然,只需要B(f1,f2)的m-r+1阶子式,这样可以在计算GCD的时候节省时间和空间。
1.2 二元多项式近似GCD算法
有两个二元多项式f1(x,y)和f2(x,y),假设degx(f1)=degx(f2)=m,degy(f1)=degy(f2)=n,其中degx(f1(x,y))表示f1(x,y)中y为常量时,多项式中变量x的最高次数,degy(f1(x,y))同理。先将和中。每个k对应相应的两个一元多项式,将前一节的一元近似GCD算法应用到这些一元多项式中,可以得到标量[2]。 将n-1代入到上述的式子中,可得到离散傅立叶变换元素的矩阵,如下所示:

其中,A(k,l)是的GCD估计值。同理可以将代入f1(x,y)和f2(x,y)中,得到单变量多项式的GCD进一步代入,然后得到另一个离散傅立叶变换元素的矩阵:

向量a(k)和b(l)可以通过最小二乘法的方法解得,如下所示:

可以通过用逆离散傅立叶变换来计算p(x,y)=gcd(f1,f2)。

2 近似GCD算法的改进
改进算法主要分为两个步骤来实现:近似GCD算法求解图像多项式的辅助因子,全变分正则化迭代解卷积。
2.1 近似GCD算法求解图像多项式的辅助因子
假设原始图像g(x,y)产生退化图像g1(x,y)和g2(x,y),对于退化图像多项式来说,一般其PSF多项式各个变量的最高次数较小,可以把g1(x,y)和g2(x,y)的近似GCD多项式的次数看成m和n。用前文引入的二元近似GCD算法,内插辅助因子h1(x,y)或者h2(x,y),即两幅退化图像的PSF,然后通过最小二乘法得到近似PSF。具体的算法流程如下所示:
输入:degx(g1)=degx(g2)=m,degy(g1)=degy(g2)=n,其中g1(x,y),g2(x,y)∈ℂ[x,y],ε∈R>0,其中ε为给定的容错度;
输出:g1(x,y)和g2(x,y)的近似辅助因子h1(x,y)和h2(x,y),其中h1(x,y),h2(x,y)∈ℂ[x,y]。
步骤1:估计出r=degx(h)和s=degy(h),即f(x,y)中两个变量的最高次数;
步骤2:用单变量多项式近似GCD算法去计算矩阵 [h(xk,yl)]∈ ℂ(m-r+1)×(n-s+1),其中:

步骤3:h(xk,yl)通过逆快速傅里叶变换计算出h(x,y),即图像多项式的辅助因子。
2.2 全变分正则化迭代解卷积
上述的近似GCD图像盲复原算法中直接使用逆滤波算法去求解复原图像,会将图像中有些区域的噪声放大,严重影响最后盲复原的结果[8]。为了解决该问题,在近似GCD算法求解出h(x,y)之后,利用全变分正则化进行非盲解卷积,解出复原图像。该算法在解卷积的同时可以更好地抑制图像中的噪声,保存好图像的边缘细节部分,为此引入以下的解卷积约束模型,如下所示:
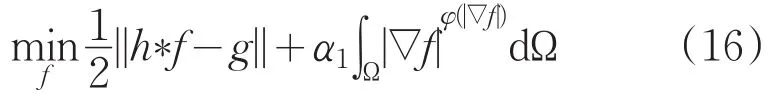

由于式(16)中点扩散函数h已知,可以根据半二次规整化理论,引入辅助变量z,w将上式转换成易求解的形式,按照w→z→f的顺序来交替最小化[11]。
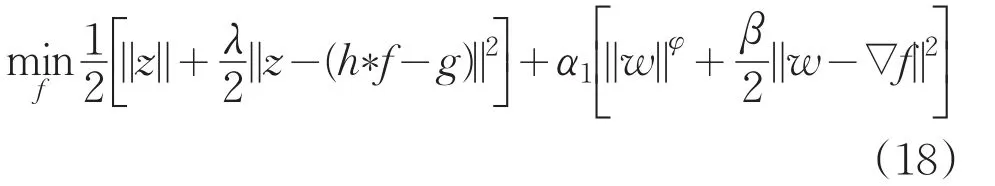
其中,λ,β为新设置的参数,φ的定义见式(17),满足λ,β→∞ ,如果‖z- (h∗f-g)‖2→0 不成立,这与上式最小化相矛盾,‖z- (h∗f-g)‖2→0必成立。同理,‖w- ∇f‖2→0必成立。对式(18)进行求偏导,可得:

矩阵范数的导数有下面的性质:
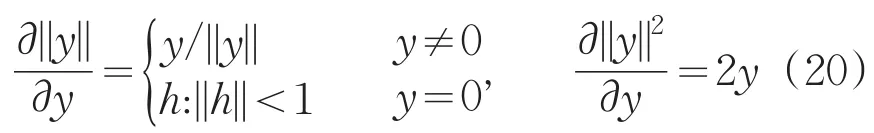

可以通过式(19)和(21)对各个变量进行求解,步骤如下所示:
(1)对w的求解
对w的求解分为两种情况:当φ=2时,可得到w的表达式如下:
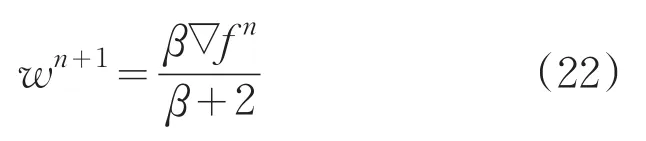
当φ=1时,可得到w的表达式如下:

(2)对z的求解

(3)对f的求解

其中,F-1表示傅里叶逆变换,“*”表示矩阵的共轭,H,G,Z,D,W分别表示h,g,z,∇,w的傅里叶变换。
2.3 改进算法的流程
针对原算法对噪声敏感的问题,改进的算法采用全变分正则化对图像盲复原的过程进行约束。该算法中使用两张退化图像g1、g2,使用近似GCD算法估算出近似PSF后,然后,用全变分正则化迭代解卷积,当满足停止迭代条件‖fn+1-fn‖>ς时,得到复原图像。算法流程如下:

输入:模糊图像g1、g2;Step1:估计出原图像多项式两个变量的最高次数;Step2:计算矩阵h(xk,yl),即点扩散函数的傅立叶变换形式;Step3:h(xk,yl)进行逆傅立叶变换,得到近似PSF;Step4:利用式(22)或者(23)对w进行更新;Step5:利用式(24)对z进行更新;Step6:利用式(25)对f进行更新;Step7:判断是否满足‖ ‖fn+1-fn>ς,如果满足执行下一步,否则返回Step4;输出:清晰图像 fn+1。
3 实验结果与分析
本文的实验环境为:处理器为Intel Core i5 3210M,操作系统为Windows7 64位操作系统,运行内存8G,仿真环境为Matlab R2016b。改进算法用全变分正则化算法取代原算法中的逆滤波算法,实验中阈值Th=1.2δ,δ为图像中局部的估计的标准差。为了验证改进算法的性能,下面设置了对比试验,对原始图像进行模糊处理,其中原始图像Lena和Peppers大小为256×256模糊核的大小为7×7,并施加不同水平的噪声,下面对Lena施加高斯噪声,对Peppers施加均匀分布噪声,用PSNR和SSIM来衡量复原图像的质量。如图2-图7给出不同情况下复原的结果,表1-表4给出相应的PSNR和SSIM。下面实验中GCD算法为文献[3]中支丽红等人提出的算法。

图2 高斯噪声水平为10-4时的复原结果

图3 高斯噪声水平为5×10-4时的复原结果

表1 两种算法复原结果的PSNR(高斯噪声)

表2 两种算法复原结果的SSIM(高斯噪声)

图4 高斯噪声水平为10-3时的复原结果

图5 均匀分布噪声水平为10-4时的复原结果

表3 两种算法复原结果的PSNR(均匀分布噪声)

表4 两种算法复原结果的SSIM(均匀分布噪声)

图6 均匀分布噪声水平为5×10-4时的复原结果

图7 均匀分布噪声水平为10-3时的复原结果
从实验结果可以看出文献[3]中近似GCD算法对噪声比较敏感,在噪声水平为10-4时,退化图像其复原效果不错,能够保持图像中的很多细节信息。但是,随着噪声水平的增大,其复原图像的质量逐渐下降,图像中的细节变得模糊,同时还出现很多波纹现象,严重降低了图像的视觉效果。这是由于噪声扰动产生的误差,在缺乏约束条件和直接逆滤波的作用下被放大。采用改进算法后,可以明显看出复原图像的视觉效果得到改善,抗噪性得到提高,可以从表1、表3中的PSNR和表2、表4中的SSIM可以看出改进算法具有较大的优势,在施加两种不同噪声的情况下,改进算法的PSNR提高了1~5dB,SSIM提高了0.09~0.3。
4 结论
本文采用全变分约束解卷积来改进近似GCD图像盲复原算法。近似GCD图像盲复原算法鲁棒性差的原因在于,缺乏约束条件和后端使用逆滤波算法。在盲复原过程中,缺乏约束条件使数值误差往下传递。其次,算法的后端处理使用了逆滤波算法,实验表明该步骤会放大图像局部的噪声。全变分非盲解卷积不仅可以抑制退化图像中的噪声,而且还可以在保存图像细节的同时完成解卷积。从仿真实验结果表明,与近似GCD图像盲复原算法相比,改进算法无论在视觉效果还是在PSNR和SSIM上均有所改进。

