基于R语言的制造质量控制与预测*

乔仁杰，宋庭新

(湖北工业大学 机械工程学院，武汉 430068)

0 引言

在现代制造企业中，产品制造过程中的质量控制无疑是企业最核心的竞争力之一。1924年休哈特(Hugh Hart)提出的控制图理论虽然能够很直观地反映质量数据的波动情况，但却忽略了历史数据对当前数据的累积影响，对于过程的小偏移检出力较弱。所以，采取联合休哈特累积和(CUSUM)控制图，增加对观测值与目标值之差的累积和来描点，利用累积数据，可以提升对质量状态小偏移的检出能力[1-2]。近年来，许多学者对质量控制理论进行了大量研究，如龚立雄等利用信息化技术设计了一套完整的质量信息系统来对质量进行实时监控与分析[3]，很好地解决了实时质量数据监控，但不能对未来质量数据进行预测与分析。江宇平等提出的一种基于赋值型误差传递网络的多工序加工质量预测建模方法，能有效预测加工误差[4]，但这种预测方法主要针对加工过程中的误差，且过程较繁琐，难以普及。R语言作为一种专门为数理统计、数据分析和统计制图开发的开源编程语言，可以快速生成质量控制图并对质量数据进行分析与预测。本文结合汽车零部件制造中花键轴的实例，利用R语言绘制联合休哈特累积和控制图并针对花键轴特点建模，选取Holt-Winters质量预测模型来对未来质量数据进行预测。这种方法可以很好地简化质量预测过程，提高质量预测效率，为解决质量预测难以在中小型企业中普及的问题提供了有效的思路。

1 质量控制理论

1.1 休哈特控制理论

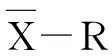
休哈特控制理论主要通过采集质量数据样本，计算标准差σ和管理上限UCL及下限LCL，当加工工序处于稳定状态时，随机误差具有一定的分布规律，总体上服从正态分布N(μ，σ)或近似正态分布。在正态分布的±3σ范围内，样品特征值出现在μ+3σ与μ-3σ上下限之间的概率为99.73%，超出该部分的概率仅为0.27%。其计算步骤如下：

(1)

(2)求样品极差R或者标准差S，其中S代表标准差σ。

(2)

(3)确定控制界限。一般控制界限选取为3σ标准差，即：

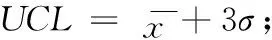
(3)

按照计算的参数绘制休哈特控制图(见图1)，图中折线代表产品质量的波动，在管制上限UCL与管制下限LCL内的波动属于可控状态，当超出则说明失控。

图1 休哈特控制图

1.2 累积和控制理论

累积和控制图是基于与历史数据比较的结果，将多次数据的波动进行整合来放大波动效果，使累积和控制图对于均值微小的偏移过程更加敏感。其一般步骤如下：

(1)求样本标准偏差σLT；

(4)

(2)求累积和图，其中Ku、Kl表示上限值和下限值，上偏差mszu与下偏差mszl参数(一般取1σ)；

(5)

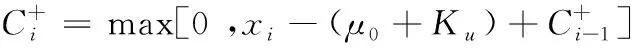
(6)

(7)

绘制的累积和控制图中有上累积线与下累积线两条折线，两条不同的绘图点让累积和控制图可以同时看到累积和上下偏移目标的情况，刻画了微小偏移的波动(见图2)。

图2 累积和控制图

通过累积和控制图发现大约在10个数据前上累积和与下累积和基本都趋于零，说明此时数据比较平稳，而之后上累积大幅的向上偏移并超过了UCL控制上线，此时说明数据整体向上偏移异常，系统处于失控状态。所以，通过联合休哈特与累积和控制图既可以直观地反应数据波动情况，又可以刻画历史数据的波动影响及对微小波动的敏感性，提高质量控制的效率及准确率。

2 案例研究

在重型汽车车桥中，传动轴联结一般采用渐开线花键联结，因此花键的加工质量非常关键[5]。某汽车零部件企业生产的花键轴产品如图3所示，其外花键测量棒间距均值要求为μ0=45.550mm，测量20组外花键跨棒距参数D作为统计样本。

图3 花键轴与外花键跨棒距D

取样本量为20，测得质量数据矩阵为：

在R语言的集成开发环境RStudio中进行编程和统计制图。使用R语言的sd()函数求出数据矩阵中的标准差σ = 0.00590517，采用3σ的管控系数，则管控中心线CL =μ0= 45.550 mm，上、下控制限为：UCL = CL+3σ = 45.53228 mm，LCL = CL-3σ = 45.56772 mm。再通过plot()函数将收集的样本数据进行描点及绘制，并附加abline()函数绘制控制图的管控线UCL和LCL，绘制的控制图如图4所示。

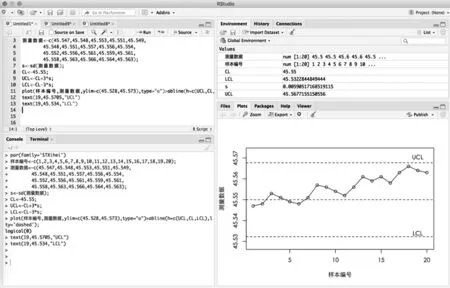
图4 在RStudio中绘制休哈特控制图

图4中的数据均处于管控上线UCL与管控下线LCL的范围之中，说明此时数据没有明显超出控制，但从图4中发现数据存在向上偏移的趋势。因此联合使用累积和CUSUM控制，如图5所示。

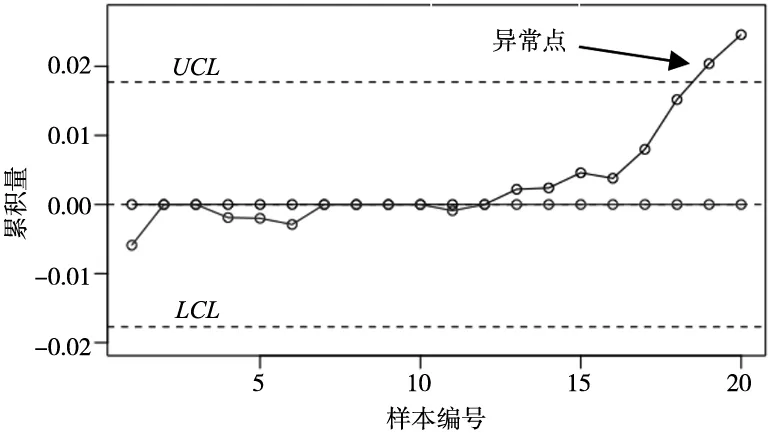
图5 联合累积和CUSUM控制图

从图5中可以发现11号样本之前的累积上下线都处于0左右，说明数据没有明显的偏移，而11号之后下累积线一直为0，上累积线大幅度向上偏移，说明此时数据整体向上偏移，从第19个数据开始，数据整体向上偏移超过控制上线，说明此时质量数据处于失控状态，需要重新检查系统找出问题原因，之后再进行系统评估。

3 质量预测

3.1 Holt-Winters指数平滑法

目前，在质量预测中最常用的时间序列分析方法是指数平滑法，该方法通过对不同时间序列数据的权重分配以及从近期到远期数据逐渐赋予收敛至零的权数，来合理利用各个时间段上的数据，从而对未来质量数据进行预测[6-8]。不同次数的指数平滑对应不同预测模型。一次指数平滑适用于无明显趋势和季节性的时间序列；二次指数平滑在第一次的基础上再进行指数平滑，增加了趋势参数但没有季节性的序列；三次指数平滑在两次指数平滑算法上增加季节参数P来对趋势进行预测，更能体现周期性变化的规律。三次指数平滑也叫Holt-Winters指数平滑法。Holt-Winters指数平滑法分为累加和累乘两种，累加是根据线性时间趋势与加法模型序列，累乘是根据线性时间趋势与乘法模型序列。由于不同季度不合格品是个数的对比，比如夏季比冬季的不合格品数多30件，所以选用累加模型。而累乘一般适用于大量数据的百分比比较[9-10]。

基于累加的Holt-Winters指数平滑公式为：

si=α(xi-pi-k)+(1-α)(si-1-ti-1)

(8)

ti=β(si-si-1)+(1-β)ti-1

(9)

pi=γ(xi-si)+(1-γ)pi-k(k=周期)

(10)

其累加Holt-Winter预测公式为：

xi+h=si+hti+pi-k+(hmodk)

(11)

其中，公式(8)中的α是平滑参数，t用来保留平滑趋势，p为季节参数，si则是i个数据的平滑值，取值为[0,1]。α越接近0，说明数据平滑后越接近i个数据的平均值，数据越平滑；α越接近1说明平滑后的值越接近当前时间的数据值，数据越不平滑。α的值通常通过具体情况进行尝试来确定最佳值。在式(8)～式(11)中，α，β，γ的值均应该多次测试与实验，使其最佳值位于[0,1]之间。s，t，p的初始值的选取对于整体算法的影响较小，通常取s0=x0,t0=x1-x1,在累加中p值默认为0[11-12]。

3.2 Holt-Winters预测过程

在R语言中预置有Holt-Winters模型包，通过调用包内的函数并配置相关参数就能建立Holt-Winters模型。将采集到的上述花键轴跨棒距数据D导入RStudio编译器中，利用R语言的ts()函数对所取数据进行时间序列化，取10为底的log对数，命名为测量距d，增加数据波动的敏感性。再调用plot()函数打印时间序列化后的数据图如图6所示。

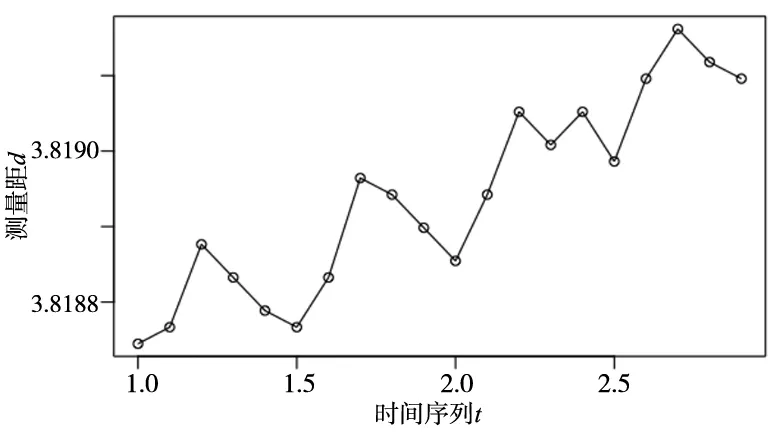
图6 时间序列化图

从图6可以看出，经过时间序列化后的图形趋势变化更加明显。时间序列t表示在时间序列下的新坐标，1.0表示第一个时间点获取的质量数据，随后表示每经过0.1个时间段获取的新的数据，这样20个样本数据分别与时间序列1.0～2.9之间的时间点对应。

接着建立Holt-Winters模型，利用R语言中的Holt-Winters()函数，将时间序列转化后的数据建模，将数据过滤为Holt-Winters模型下的趋势图(见图7)，其中无圆点的折线表示原数据经过Holt-Winters三次指数平滑计算后的观察值，而圆点折线表示对现有数据进行Holt-Winters过滤后的趋势变化。

图7 Holt-Winters模型图

根据图7中的Holt-Winters模型发现数据趋势与原数据基本吻合，再调用R语言包中的forecast()函数进行数据预测，其中需要设置的参数h代表预测多少个数据(这里取h=8代表预测8个数据)，预测结果见表1。

表1 Holt-Winters预测结果

表1中，时间序列3.0对应的预测数据3.819082便是对第21个未来样本的预测值，以此类推。Lo 80与Hi 80表示预测的一级波动区间即80%的置信区间为(Lo 80, Ho 80)，同理Lo95与Hi95表示二级波动区间，其范围比一级波动区间更大，可信度更高但数据预测更不准确，波动区间为实际数据波动提供参考。最后根据质量控制理论计算出来的UCL与LCL管控上下线取对数后的新UCL与LCL上下线进行质量管控，通过abline()函数附加在原图上，再将预测值与原数据值覆盖一并绘图，如图8所示。

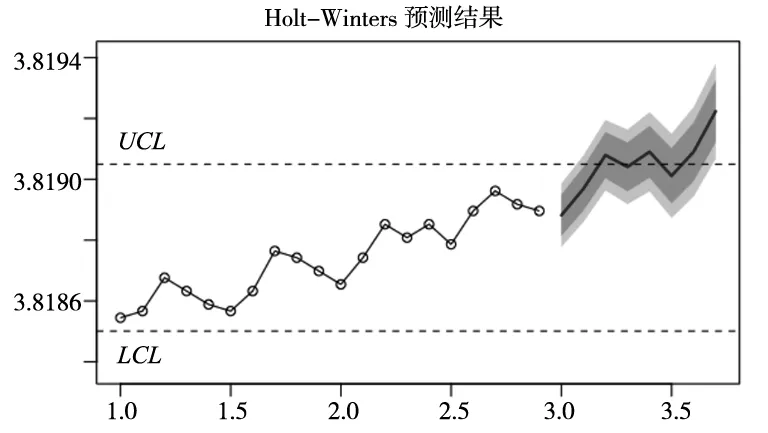
图8 预测数据及波动区间

根据图8发现当前的数据(圆点折线)并没有超出UCL与LCL管控线，但是根据预测的结果(无圆点折线)说明:预测值越来越向UCL管控上线偏移，最终将会超出管控上线，未来可能出现质量问题。所以此时应该提前预警，对可能存在的质量问题做出检测与排查，保证未来质量也能处于可控状态，避免质量问题的发生。

4 结论

本文基于R语言结合联合休哈特累积和控制理论，对花键轴制造过程进行质量控制，并高效地建立Holt-Winters模型进行质量预测。对未来可能发生的质量问题进行预警与排查，将质量问题解决在萌芽之中。本文质量控制与预测方法成本低廉，便捷高效，适合向中小型制造企业进行推广与借鉴。下一步，还可以深入研究R语言与质量管理信息系统(QMIS)的集成问题，将质量控制理论和预测方法融入到QMIS的开发中，以提高企业质量管理水平和质量信息化目标，为实际生产提供有益的管理工具和手段。