DGM(2，1)模型在沉降预测中的应用

石勇，张西军，肖先华

(1.重庆市勘测院，重庆 401121； 2.重庆市智能感知大数据产业技术协同创新中心，重庆 401121；3.沈阳市勘察测绘研究院，辽宁 沈阳 110004)

1 引 言

通过对监测点进行沉降监测，掌握监测点的位置变化，监测点的累计沉降量较多情况下存在随着周期的增长沉降速度变缓的情况。变形预报是变形监测不可或缺的环节，如何能精确地预测出沉降变化，是正待解决的问题。灰色预测是一种预测沉降量的方法，传统的预测模型有GM(1，1)、DGM(1，1)、Verhulst[1～3]。在此基础上发展出了许多模型，如NDGM(1，1)、GOM(1，1)、残差GM(1，1)、综合优化GM(1，1)、间接DGM(1，1)、动态DGM(1，1)、优化Verhulst模型等[4～10]。这些模型与其他模型相结合，产生新的组合模型，例如GM-AR、BP-GM、Verhulst-BP等等[11～14]。

随着监测周期的增加，沉降速度变缓，本文对这种特性的累计沉降量序列进行分析预测。结合变形监测实例，利用GM(1，1)、DGM(1，1)、DGM(2，1)三种模型对监测点的累计沉降量进行预测，结果表明GM(1，1)模型、DGM(1，1)模型不能适应累计沉降量序列的变化，预测值严重偏离实测值，预测值失真。DGM(2，1)模型适应数据列变化的能力较强，可以合理地做出预测，精度高于另外两种模型。

2 GM(1，1)模型

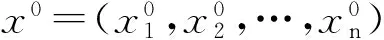
建立关于序列x1的白化方程：

(1)

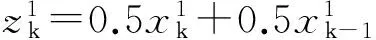
通过最小二乘法求得：

[a，b]T=(BTB)-1BTYN

(2)

方程(1)的解为：

(3)

累减生成可得还原数据为：

(4)

3 DGM(1，1)模型

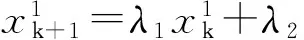
(5)

称为离散灰色模型，即DGM(1，1)模型。

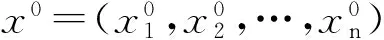
令λ=[λ1，λ2]T为参数列，由最小二乘法求得：

λ=[λ1，λ2]T=(BTB)-1BTY

(6)

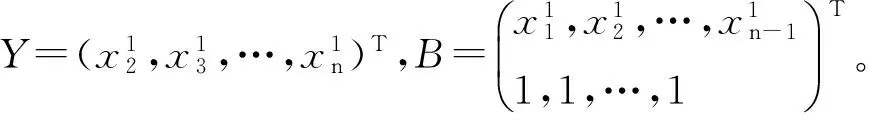
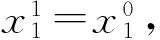
(7)

还原值为：

(8)

4 DGM(2，1)模型

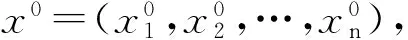
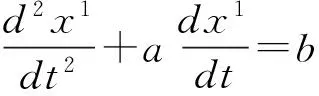
(9)

称之为DGM(2，1)模型的白化方程。

令U=[a，b]T，通过最小二乘法求得：

U=(BTB)-1Y

(10)

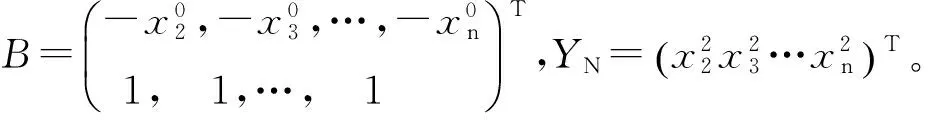
求解白化方程(9)得到：

(11)

由式(11)作累减还原得预测值序列为：

(12)

5 实例分析

对某码头附近边坡进行变形监测，本监测共布设33个监测点，共进行15周期，每5天为一观测周期。本文选取其中的一点进行分析，该点15周期的累计沉降量如表1所示。

观察表1的累计沉降量值，发现累计沉降量在前5周期增长速度较大，第6～8周期增长速度开始放缓，第7周期以后随着周期的增长，累计沉降量增长速度基本呈逐渐减小的趋势。

以2～8周期的累计沉降量为建模数据，运用MATLAB实现具体的算法，得到三种模型在9～15周期的累计沉降量预测值，三种模型的预测结果如表2所示，平均相对误差如表3所示。

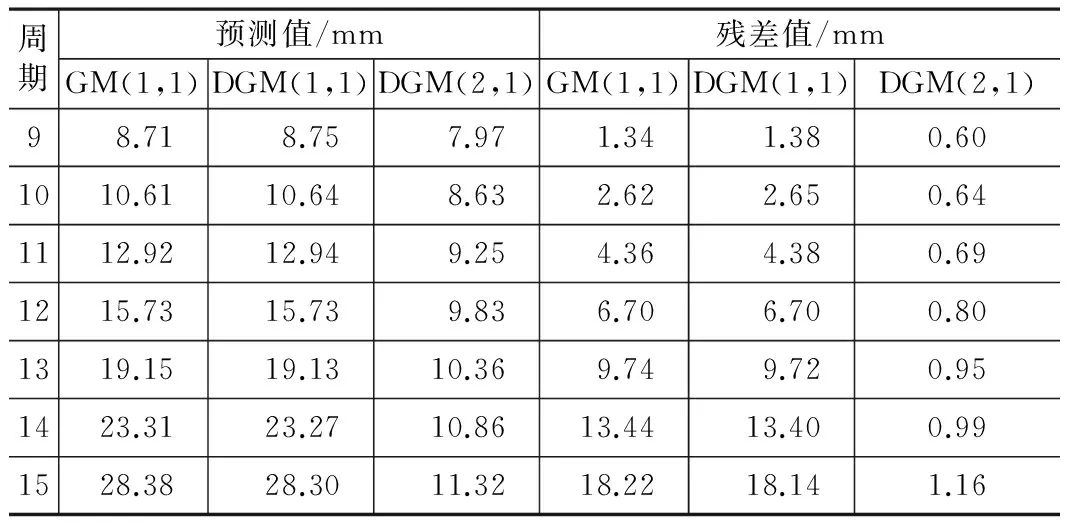
三种模型的预测值及残差值 表2

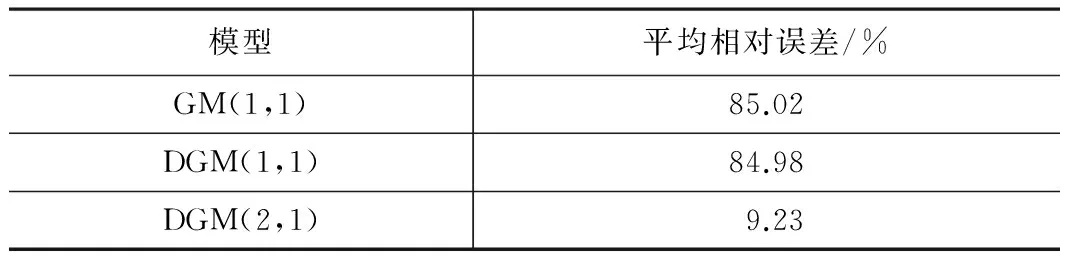
三种模型的平均相对误差 表3

比较三种模型的平均相对误差，GM(1，1)模型和DGM(1，1)模型的平均相对误差远大于DGM(2，1)模型。DGM(2，1)模型残差值较小，远小于GM(1，1)模型和DGM(1，1)模型的残差值，这说明DGM(2，1)模型的预测精度远高于另外两种模型，DGM(2，1)模型取得了较好的预测效果。GM(1，1)模型和DGM(1，1)模型的残差值已经达到不可接受的程度，模型已经不再适用。

为更直观地表现出预测值和实测值的偏离程度，绘制了三种模型的预测曲线。如图1所示：

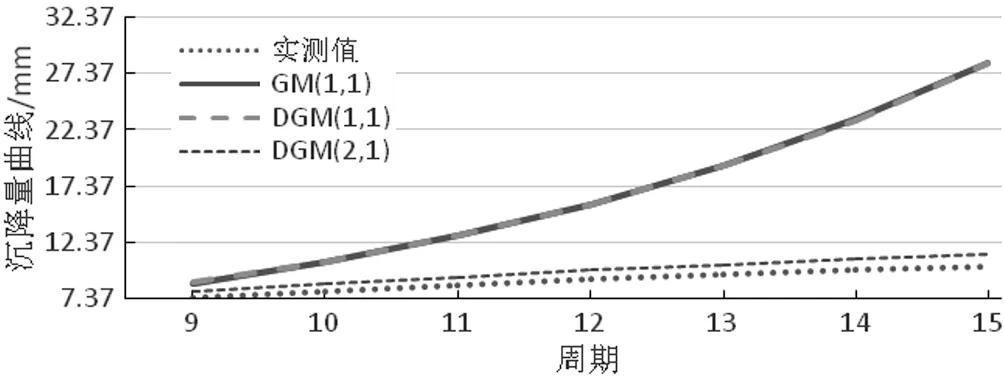
图1 三种模型预测曲线

图1反映了预测值与实测值的接近程度，DGM(2，1)模型预测值十分接近实测值，可真实地反映实测值的变化，随着周期增长并没有出现大幅度偏离实测值的情况，表现出了良好的预测效果。另外两种模型的预测值已经严重偏离实测值，预测值完全失真。

分析原始数据，前期数据增长速度较快，随着周期的增长，沉降速度逐渐较小，存在较为明显的沉降加速度。使用GM(1，1)模型和DGM(1，1)模型进行预测时，这两种模型不能及时感应到沉降速度的变化，预测过程中没有顾及沉降加速度对预测值的影响，预测值持续大幅度增大，致使预测值与实测值出现严重偏差。GM(1，1)模型和DGM(1，1)模型对数据列变化的适应性较差，而DGM(2，1)模型在对这种前后增长速度不同的数据列进行预测时，预测过程中减弱了沉降加速度对预测值的影响，可以较好地适应数据列的变化，预测精度较高。

6 结 语

对于前期数据增长速度大于后期的累计沉降量序列，利用GM(1，1)模型和DGM(1，1)模型进行预测，这两种模型不能及时感应到沉降速度的变化，预测值持续大幅度增长，致使预测值与实测值出现严重偏差，预测值失真。而DGM(2，1)模型在面对这种类型的数据列时，对数据列变化的适应性较好，预测过程中减弱了沉降加速度对预测值的影响，预测精度远高于GM(1，1)模型和DGM(1，1)模型。