基于最小二乘法的NAR模型及其在沉降预测中的应用

范成成，张俊

(贵州大学矿业学院，贵州 贵阳 550025)

1 引 言

现代建筑物的地基压力不断增大，必然会引起建筑物地基及周边环境的形变，当变形达到一定的极限，就会对建筑物主体结构产生破坏，间接对周围环境造成巨大的经济损失。目前，针对不同建筑的沉降监测数据处理预报，不同的研究人员提出了不同的方法。对于软土路基矿区等监测多见AR模型[1，2]对其进行处理分析。对于隧道的基坑监测多使用灰色模型[3，4]进行处理。当然，也有利用其他模型来进行平差处理及预报，如Gompertz模型、Verhulst优化模型、Lstsvr模型等[5，6]。

本文在AR模型的基础上，提出了NAR模型[7，8]的最小二乘法解算方法解算模型的参数并用所求参数带入模型对所观测的数据进行处理和模拟预报及精度评定，再与AR模型所处理的数据及原始观测值进行对比，由二者对比结果分析得出，NAR模型在沉降监测预报中的可行性，且与AR模型所预报值相比较为稳定。

2 模型简介

2.1 AR模型的最小二乘法

AR模型是一种线性时间序列模型，在工程实践和定位导航等方面都有着广泛应用[9，10]。AR模型公式如下：

(1)

对式(1)用矩阵形式可以写为：

L=BX

(2)

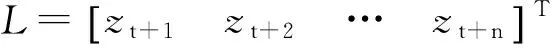
(3)

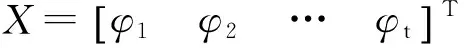
X=(BTPB)BTPL

(4)

以上就是AR模型的最小二乘解法。其单位权中误差可用下式进行评定：

(5)

其中V=BX-L。P为权阵，定权需要根据实际观测情况。一般观测都是在同等条件下进行，故P可视为单位权矩阵。

2.2 基于SVD的AR模型总体最小二乘解法

总体最小二乘平差方法是一种顾及系数矩阵误差的一种解算方法，此方法的提出是因为仅用经典最小二乘平差会忽略掉系数矩阵的误差，因此，总体最小二乘的提出大大解决了此问题。

结合AR模型，其总体最小二乘的函数模型可以写成下列形式：

(A+△A)X=L+△L

(6)

式中△A表示系数矩阵的误差，△L表示观测值误差。将模型进一步表示为：

(A+EA)X=L+e

(7)

式(7)中：

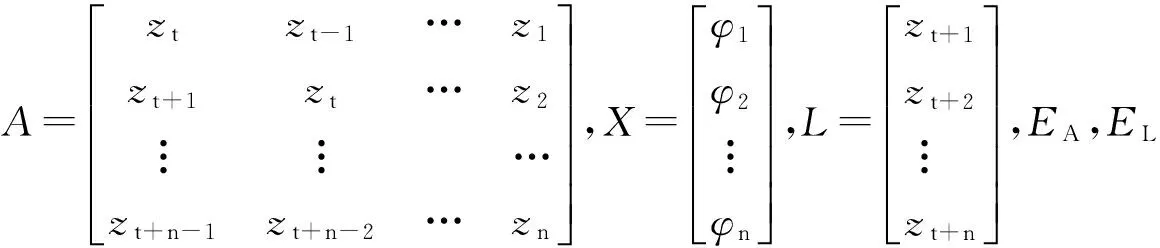
将增广矩阵进行奇异值分解：

(8)

上式中，

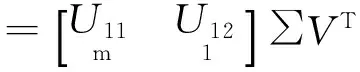
所以，总体最小二乘的参数解便可由VT的最后一列求得，即：

(9)

以上就是AR模型的总体最小二乘奇异值解法，其单位权中误差也可用下式进行评定[11]：

(10)

同样V=AX-L。

3 NAR模型及其最小二乘解法

NAR模型也是一种时间序列的非线性自回归模型，其模型公式为：

zt=g(zt-1，zt-2，…，zt-p)+εt

(11)

式中g(zt-1，zt-2，…，zt-p)表示非线性函数，t为时间序列，其值为1，2，…N。上式可用多项式的非线性AR模型进行逼近[8]，即：

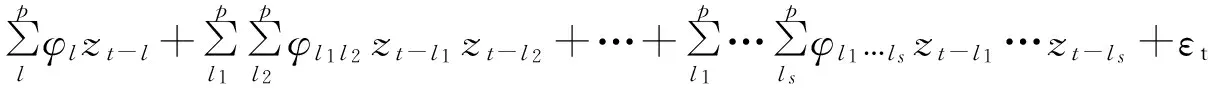
(12)

利用式(12)结合最小二乘法，将其写为矩阵形式：

L=BX+ε

(13)

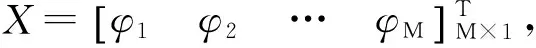
S为多项式阶数。所以由系数矩阵B，观测值L，利用经典最小二乘平差得出参数求解公式：

(14)

其余部分与AR模型最小二乘解法一致。

4 算例分析

4.1 实测沉降数据

为了验证此模型的可行性与精度，本文采用文献[11]中的例题5.6的实测沉降数据来对NAR模型进行验证，并与AR模型进行对比。此实测数据用AR(3)模型进行拟合，故在NAR模型中也效仿AR模型采用3阶进行参数求解。

用本文模型的最小二乘算法、AR最小二乘法及其SVD法三种方法所引用的数据所求得的参数估值及单位权中误差如表2所示。表1所示的是三种平差方法所求得的平差值和实测观测沉降数据。图1显示了三种方法平差结果和原始观测值的残差绝对值的对比。

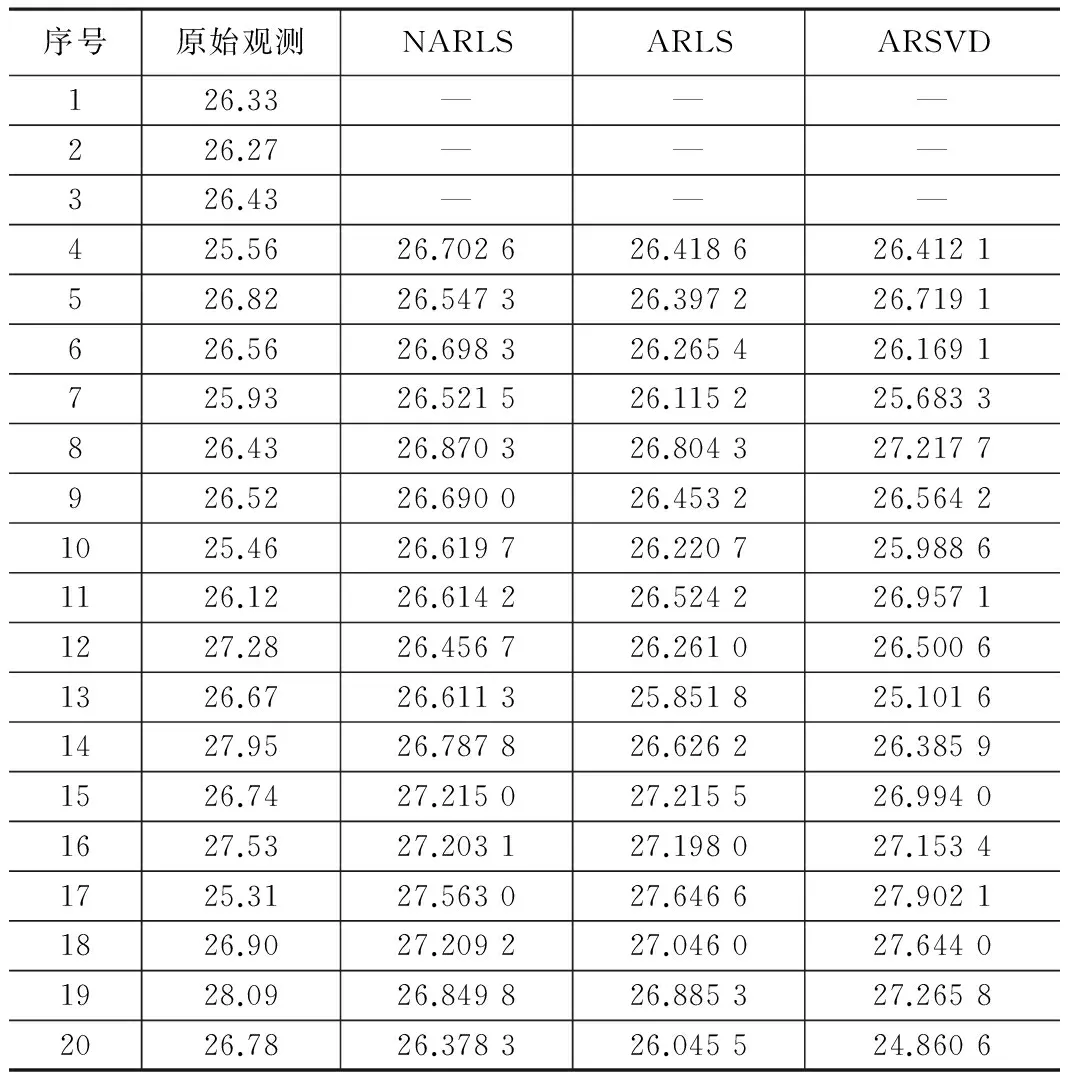
形监测点的实测沉降数据 表1

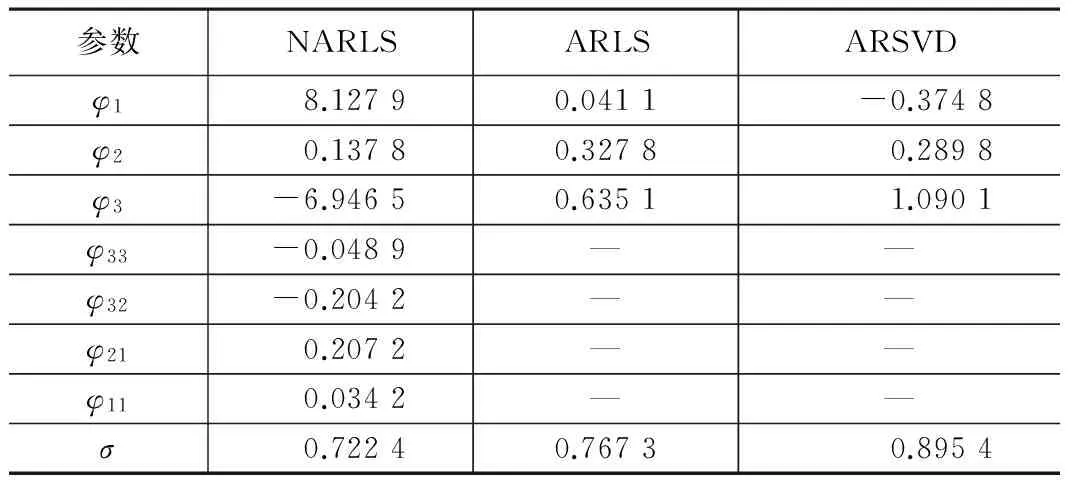
三种方法的参数值及单位权中误差 表2

从表2可以看出AR模型的最小二乘法和其SVD法所求的单位权中误差明显大于NAR模型所求得的单位权中误差，由表1和图1可知，NAR模型的最小二乘和AR模型的最小二乘平差结果比较接近，而AR模型的SVD法的结果与前两者相差较大。一方面可能是由于总体最小二乘方法的奇异值分解理论未完善，另一方面可能由于本文所引用的数据为非平稳的自回归时间序列[9]。在其他期两种模型的最小二乘法走势相对一致时，可以看出第13期、17期、16期的NAR模型处理的结果较好。

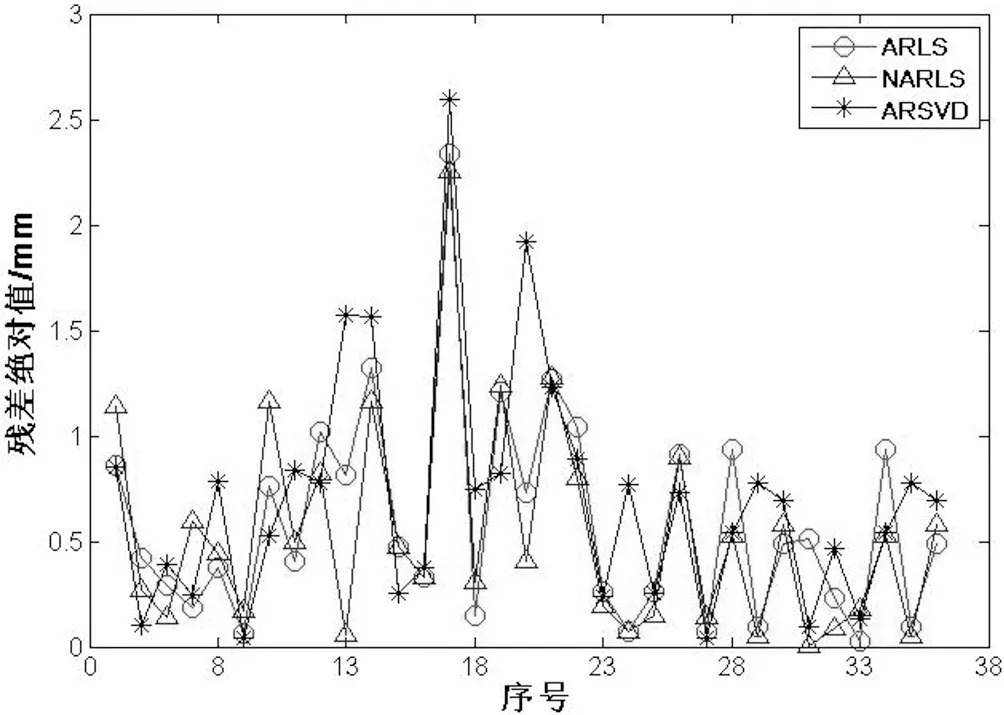
图1 三种方法平差结果与原始观测值的比较

4.2 预报分析

前文检测了NAR模型方法的内符合精度，接下来用前30期的观测值来验证NAR模型的外符合精度。也是采用两种模型的最小二乘法和AR模型的SVD法求解系数并预测31期到36期的沉降数据。根据前30期的实测数据所求得的参数及预报值如表3所示，图2所表示的是NAR模型LS法、AR模型的LS法和AR模型SVD法的预报结果与实测观测值的残差绝对值对比，图3是三种方法与原始值的走势对比。

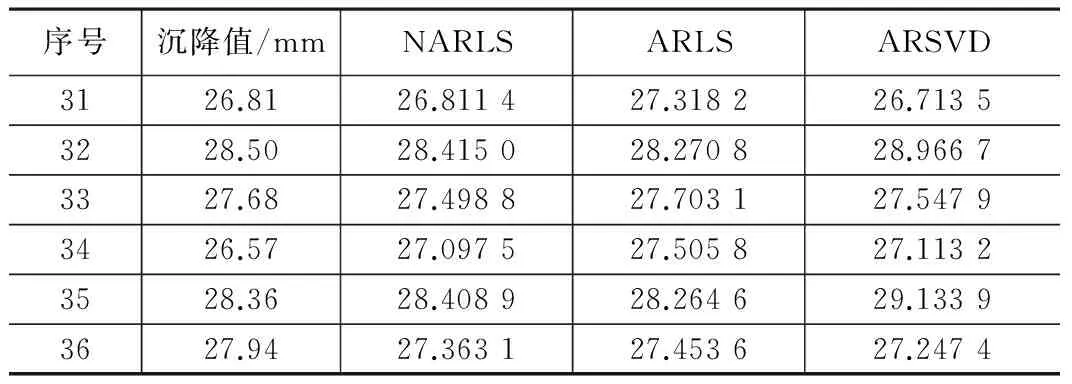
四种方法的预报 表3

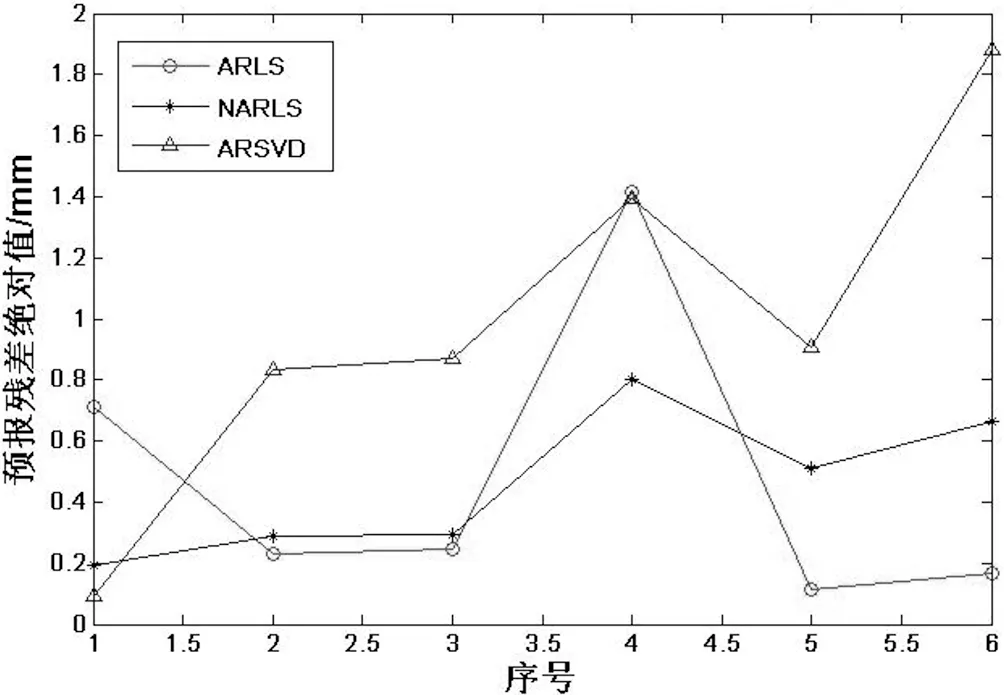
图2 三种方法预报结果的残差绝对值比较

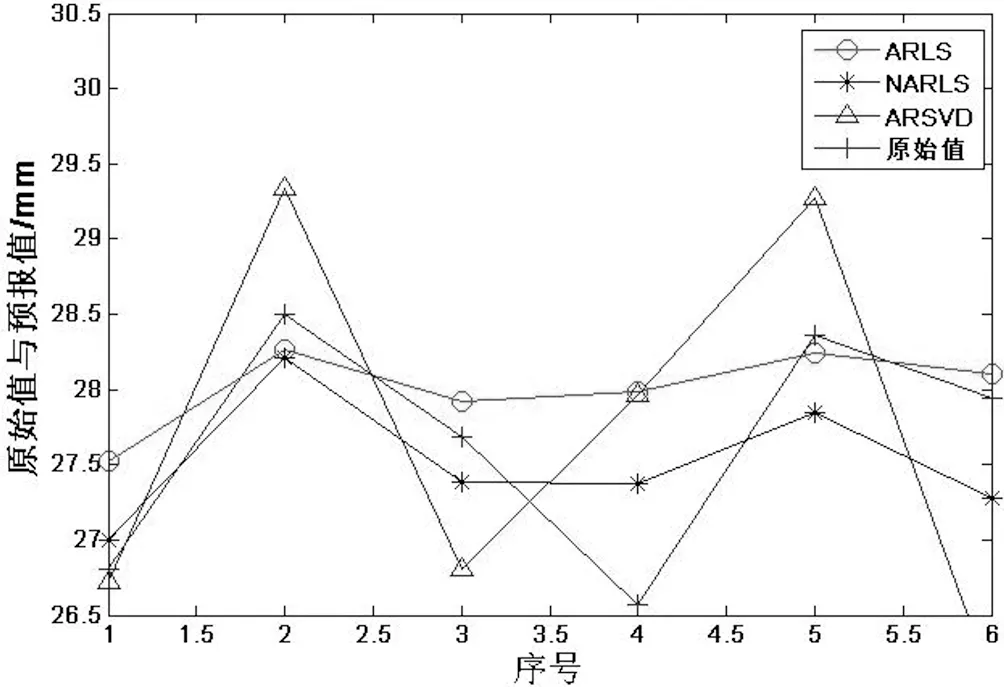
图3 三种方法预报值与原始值对比

经过计算，NAR模型LS法、AR模型LS和SVD法预报值的单位权中误差分别为 0.775 0、0.809 1、1.036 2。可见NAR的单位权中误差最小。由表3和图2可以看出，在第31期～第36期的数据中，NAR模型所预报的值与真值相比，效果相对于AR模型来说较稳定，波动性小。AR模型的SVD方法所预报的效果波动性大且效果最差；图3可以看出NAR模型预测值的折线比较靠近原始观测值，且结合图2、图3，在第34期可以看出当AR模型的波动较大时，NAR模型预测结果较好，可见NAR模型在处理此类3阶数据时的抗差力较强于AR模型。所以，NAR模型的外符合精度在此也能得以验证。

5 结 语

通过以上的结果证明，NAR模型应用在沉降变形监测的工程实例中是可行的，无论是NAR模型还是AR模型，由于其模型的特殊性可知，其观测向量和系数矩阵的误差同源，经过多次的重复迭代，系数矩阵元素误差也会影响观测向量。尽管经典最小二乘平差法理论上不能处理系数矩阵误差，宜采用整体最小二乘法，但是，由于整体最小二乘法的理论仍未完善导致基于SVD法的AR模型总体最小二乘结果较差。本文对实测数据处理结果可以看出基于最小二乘的NAR模型在变形沉降数据处理中可以得到比AR模型更高更稳定的预测外符合精度。