基于组合激活函数的CNN 应用研究

周月鹏，卢喜利

（韶关学院 信息科学与工程学院， 广东 韶关512005）

2012 年Hinton 通过卷积神经网络（Convolutional Neural Network，CNN）解决了ImageNet 问题并取得成功之后［1］，CNN 的应用领域越来越广，主要包括图像识别和分类［2］、语音识别［2］、自然语言处理［3］、立体视觉匹配［4-5］等领域.CNN 通过模拟动物大脑的运行机理，实现对象的判断识别过程.在CNN 模型中，神经元的特征首先进行卷积运算，然后通过激活函数将神经元的特征映射到下一层［6］，激活函数提高了CNN模型的表达能力，可以模拟复杂的数据模型.

在深度学习领域最初采用的激活函数包括Sigmoid 函数［7］和Tanh 函数［8］.Sigmoid 函数主要将输入值映射到［0，1］，在特征相差不是特别大时，Sigmoid 函数效果比较好，能很好的解决二分类问题，但在反向传播过程中容易出现梯度消失的情况.Tanh 函数将输入值映射到［-1，1］，Tanh 函数在有明显特征差异时的效果很好，但和Sigmoid 一样，依然存在梯度消失的问题.2010 年Hinton 提出了ReLU 函数作为激活函数，有效缓解了Sigmoid 函数和Tanh 函数中存在的梯度消失问题［9］.2017 年Prajit R 等人提出了Swish 函数，和ReLU 类似，Swish 函数是无上界但有下界的，不同的是Swish 函数是光滑但非单调［10］.当层数超过40 层时，ReLU 函数准确率下降的速度比Swish 函数要快，目前在深度学习领域应用最广泛的激活函数是ReLU［10］.每个激活函数都有各自的优点，不同的激活函数都有适应的数据集，在实验中通过在CNN 的不同层中采用不同的激活函数，通过组合的方式实现对象识别准确率的提高.

1 相关工作

1.1 卷积神经网络

CNN 是一种深层前馈型神经网络，最常用于图像领域的监督学习问题，比如图像识别、计算机视觉等［11］.LeCun 于1998 年提出CNN 模型，并将该模型应用到手写字符的检测中［12］.CNN 是一种局部连接、权值共享的神经网络模型，每一层都包含多个二维平面，每个平面又包含多个神经元［13］.CNN 具有局部感知、参数共享、多卷积核、池化、稀疏性限制等优势［14］，被广泛应用在图像识别领域.LeNet-5［12］是LeCun 设计的用于手写数字识别的CNN，LeNet-5 包括卷积层、下采样层、全连接层3 部分，该系统在小规模手写数字识别中取得了较好的结果.

CNN 的基本结构包括输入层、卷积层、池化层、全连接层和输出层［15］.和全连接神经网络相比，CNN是一种带有卷积结构的深度神经网络.CNN 权值共享的特性减少了网络中参数的个数，降低了网络模型的复杂度，减少了权值的数量，缓解模型训练过程中的过拟合现象，减少参数同样可以减少在运算过程中占用的内存量［16］.

CNN 本质上是输入到输出的一种非线性映射，它不需要输入和输出之间精确的数学表达关系和严格的推导过程，却能够有效地反映输入和输出的非线性关系，这也是判别模型是否合适的重要依据［3］.2014 年CNN 有了很大的改进，深度学习技术也在这一年快速成长.随着CNN 网络层数的增加，可以提取出图像中的更多的高维特征，提取到的特征也更抽象［14］.其模型见图1.

1.1.1 卷积层

卷积层首先对上一层特征进行卷积运算，然后通过激活函数运算，就得到输出特征.图1 中C1、C3 是卷积层，每个圆圈代表一个神经元，神经元的运算见图2.

第i 层的神经元一定与i+1 层卷积范围内的神经元连接，第i 层中每个神经元的值与对应权重相乘后相加再加上偏置值b，f 是激活函数，通过激活函数完成输入和输出之间的非线性变换，即：在

其中式（1）中ω 是每一个卷积层和上一层之间每个连接上的权值，x 是每个卷积层输入的神经元的值，b是偏置值.通过激活函数运算后，得到下一层对应神经元的值.式（2）中f 是激活函数，使得输入值通过非线性变换后接近目标值.随着层数的增加，非线性变换的次数增加，可使模型逼近任何非线性函数，更好的拟合其它的非线性模型.

图1 CNN 模型

图2 神经元的运算

1.1.2 池化层

图1 中S1、S3 为池化层. 池化层的作用是降低卷积结果的分辨率来获得具有空间不变性的特征［17］，同时池化层可以实现特征的二次提取，它的每个神经元通过对局部接受域进行池化操作［15］.池化操作包括最大池化、平均池化、最小池化，池化的主要优点在于可以实现图像变换不变性、特征表达的紧凑性、对噪声和扰乱的鲁棒性以及扩大局部感受野［18］.

1.1.3 全连接层

图1 中F1 为全连接层，全连接层将池化运算之后的特征拼接为一维特征作为输出层的输入，全连接层神经元的值通过对输入加权求和，并通过激活函数的运算得到［19］.

1.2 激活函数

激活函数为CNN 引入非线性变换，通过非线性变换提高网络的表达能力，影响了神经网络的收敛速度［20］.在传统的CNN 中，激活函数一般使用饱和非线性函数，如Sigmoid 函数和Tanh 函数，和饱和非线性函数相比，不饱和非线性函数可以解决梯度爆炸和梯度消失问题，同时可以加快收敛速度，使得模型在训练 过 程 中 更 稳 定［20］.

激活函数主要包括：Sigmoid、Tanh、ReLU［22］、Maxout［21］、Softplus 和Swish［10］，以及ReLU 的变形Leakly ReLU、Parametric ReLU、Randomized ReLU、ELU 等，本文采用比较常用的5 个激活函数，Sigmoid、Tanh、Re-LU、Softplus 和Swish 进行组合实验.

1.3 Dropout 方法

过拟合（over-fitting）［23］是指模型在训练过程中参数过度拟合训练数据集，而对训练集之外的测试集效果不好，影响模型在测试数据集上的泛化性能的现象［24］.Hinton 等［25］提出的Dropout 方法，在训练过程中根据设定比例随机忽略一些节点的响应，这些节点不参加CNN 的前向传播过程，也不参加后向传播过程［26］，减轻了传统全连接神经网络的过拟合问题，有效地提高了网络的泛化性能［24］.目前CNN 的研究大都采用ReLU+ Dropout 方法，并取得了很好的分类性能［27］，在实验过程中采用了Dropout 方法.

2 组合激活函数模型

2.1 算法模型

在经典的CNN 模型中，调整每个卷积层使用的激活函数，运算结果作为下一层神经元的值.在CNN中，模型层数不同，采用数据集不同，取得最好测试准确率的组合方式也不相同.其中4 个卷积层和1 个全连接层的组合函数模型见图3.

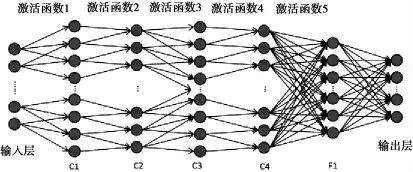
图3 组合不同激活函数的CNN 模型

图3 中包含5 个使用激活函数的层 （池化层在图中没有标出），5 个激活函数可以从Sigmoid、ReLU、Tanh、Softplus 和Swish 中进行选择、组合，通过实验发现取得最高准确率的组合模式，在系统投入使用时针对不同的数据集进行不同的设置.

2.2 实现方法

实验过程中，根据各个激活函数的不同特点，笔者在实验过程中选用的激活函数包括：Sigmoid、Re-LU、Tanh、Softplus 和Swish，分别进行组合，图3 模型中共包含3 125 种组合方式，随着层数的增多，组合的结果会越来越多. 在针对两个数据集的测试中，MNIST 数据集采用C2_F1 （两个卷积层和两个全连接层）、C3_F1 和C4_F1 的3 个模型进行实验.CIFAR-10 数据集的采用C1_F2、C2_F2、C3_F2 和C4_F2 的4个模型进行实验.

2.3 实验参数设置

数据集MNIST 采用的网络模型输入层是28×28 的手写字体图像，卷积层都采用3×3 的卷积核，卷积步长为1，第一个卷积层通道数是32，第二个卷积层通道数64，第三个卷积层通道数128；模型中ActFun采用1.2 中提到的5 个激活函数中的任意一个；池化层采用最大池化，池化层窗口大小是3×3，步长为1；每个池化层之后都使用dropout 进行处理，keep_prob 值为0.7，即30%的神经元节点在前向传播和反向传播过程中不参与训练过程的运算，但测试过程中所有的神经元都要参与运算，即keep_prob 值为1；全连接层中所有的神经元都和下一层的神经元相连接，两个全连接层的神经元个数设置为625；最后是输出层，通过归一化函数Softmax 完成模型的运算输出；模型中learning_rate 值为0.001，training_epochs 值为15，batch_size 值为100，具体模型见图4.

数据集CIFAR-10 采用的网络模型输入层是经过处理后的24×24 的图像，卷积层都采用5×5 的卷积核，卷积步长为1，3 个卷积层的通道数都是64；模型中ActFun 也采用1.2 中提到的5 个激活函数中的任意一个；池化层采用最大池化，池化层窗口大小是3×3，步长为2；全连接层中所有的神经元都和下一层的神经元相连接，第一个全连接层的神经元个数设置为384，第二个全连接层的神经元个数设置为192；最后通过归一化函数Softmax 完成模型的运算输出；模型中learning_rate 值为0.1，training_epochs 值为350，batch_size 值为128.具体模型见图5.

图4 数据集MNIST 采用的模型

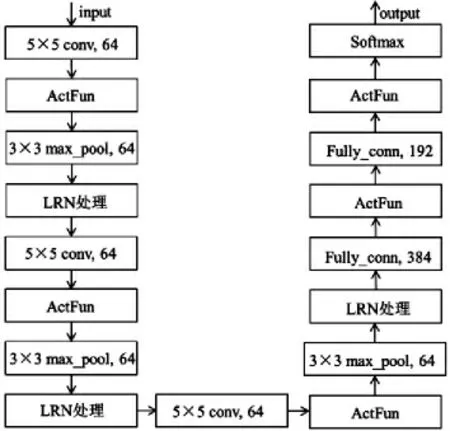
图5 数据集CIFAR-10 采用的模型

3 实验结果及分析

3.1 实验数据集

组合激活函数模型在MNIST、CIFAR-10 两个数据集上完成测试.

MNIST 数据集是包含0~9 十个手写数字组成的数据集，通常用于训练各种图像处理系统［29］，该数据集共分为10 类，包含60 000 张训练图像和10 000 张测试图像，每个图像大小为28×28 像素.

CIFAR-10 数据集分为10 类，每一类有6 000 张彩色图像组成，其中包含50 000 张训练图像和10 000张测试图像，所有图像大小都是32×32 像素.在训练和测试过程中，通过对图片的处理，输入图片大小为24×24 像素.

3.2 实验结果分析

3.2.1 MNIST 数据集实验结果分析

针对MNIST 数据集的测试中，分别采用C2F1、C3F1 和C4F13 个模型进行测试.单一激活函数的准确率见表1.C2F1、C3F1 和C4F1 的3 个模型准确率前5 的组合方式分别见表2，表3，表4.

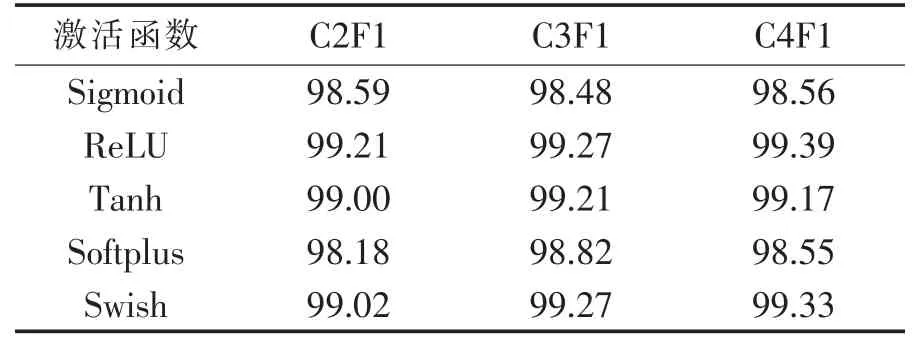
表1 单一激活函数在不同模型的识别准确率 %

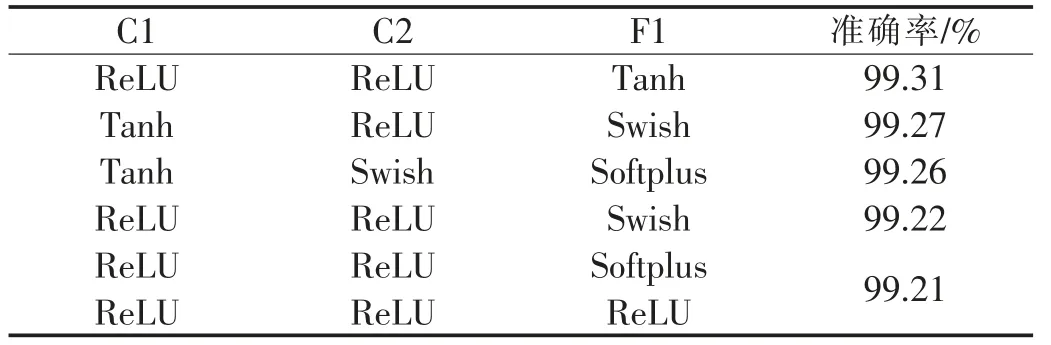
表2 模型C2F1 中激活函数组合识别准确率前5 的组合方式

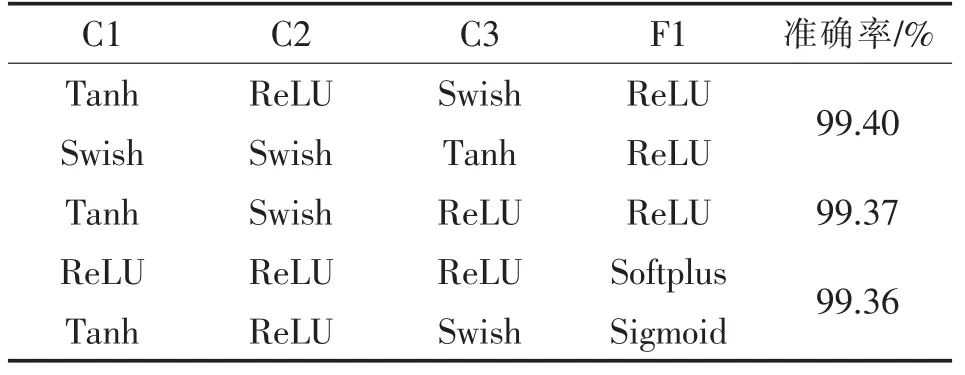
表3 模型C3F1 中激活函数组合识别准确率 前5 的组合方式

表4 模型C4F1 中激活函数组合识别准确率前5 的组合方式

从表1~表4 的实验数据可知，3 个模型中组合的激活函数比单一的激活函数能取得更好的识别准确率. 针对MNIST 数据集，3 个模型中最好的是4 个卷积层和1 个全连接层，4 个卷积层全部采用ReLU 作为激活函数，全连接层采用Swish 作为激活函数，识别的准确率达到99.48%.

3.2.2 CIFAR-10 数据集实验结果分析

针对CIFAR-10 数据集的测试中，分别采用C1F2、C2F2、C3F2 和C4F2 的4 个模型进行测试.单一激活函数的准确率见表5.C1F2、C2F2、C3F2 和C4F2 的4 个模型准确率前5 的激活函数组合方式分别见表6~表9.

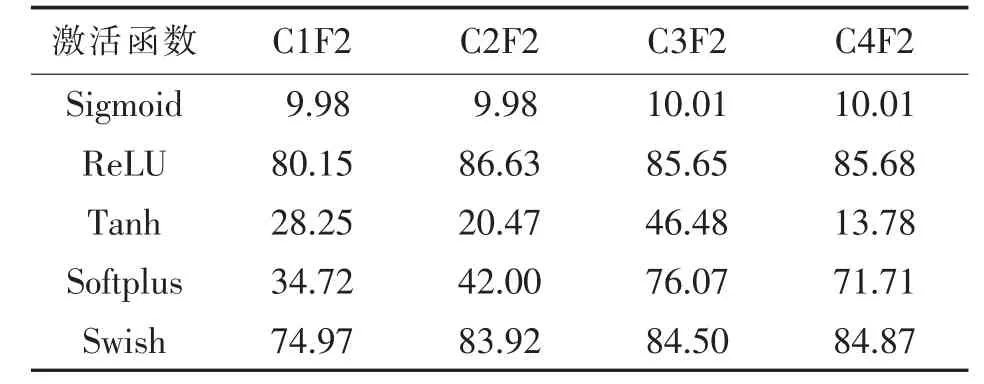
表5 单一激活函数在不同模型的识别准确率 %

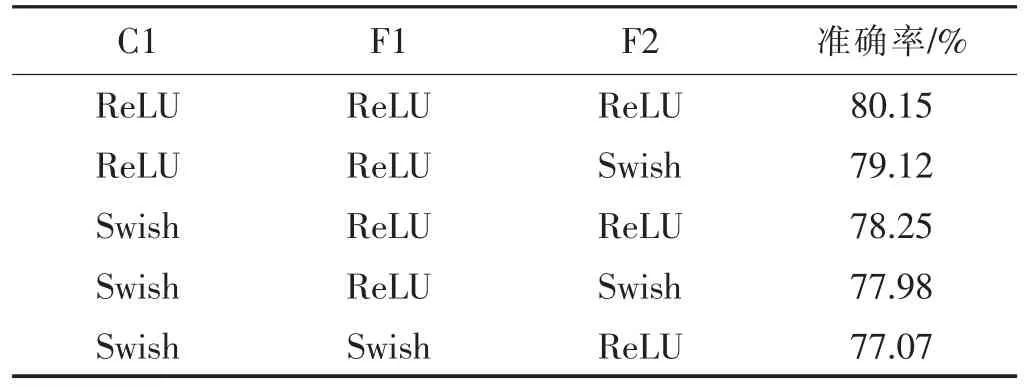
表6 模型C1F2 中激活函数组合识别准确率前5 的组合方式

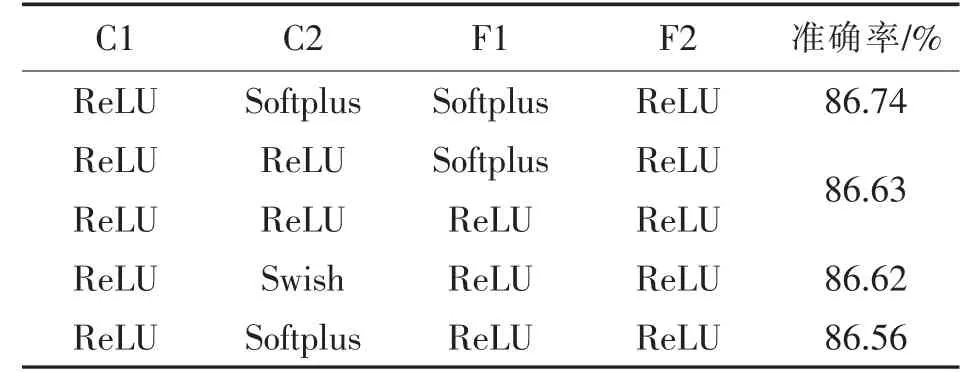
表7 模型C2F2 中激活函数组合识别准确率 前5 的组合方式

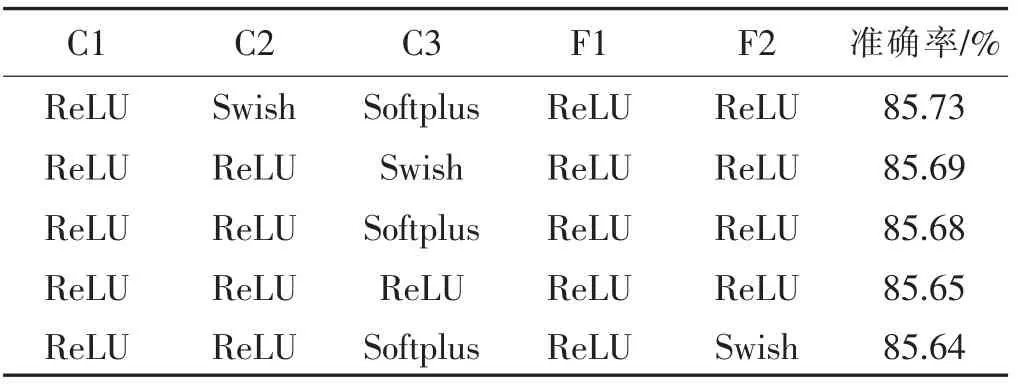
表8 模型C3F2 中激活函数组合识别准确率前5 的组合方式

表9 模型C4F2 中激活函数组合识别准确率前5 的组合方式

从表5~表9 的实验数据可知，除了C1F2 模型之外，其它3 个模型中组合的激活函数比单一的激活函数能取得更好的识别准确率.针对CIFAR-10 数据集，最好的模型是两个卷积层和两个全连接层，两个卷积层分别采用ReLU 和Softplus 作为激活函数， 两个全连接层分别采用Softplus 和ReLU 作为激活函数，识别的准确率达到86.74%.

4 结语

通过组合不同激活函数的实验可以发现，在MNIST 和CIFAR-10 数据集的图像识别过程中，采用组合激活函数的模型可以比采用单一激活函数取得更好的识别准确率.MINST 数据集中， 模型选用4 个卷积层和1 个全连接层，4 个卷积层全部采用ReLU 作为激活函数，全连接层采用Swish 作为激活函数；CIFAR-10 数据集中，模型选用两个卷积层和两个全连接层，两个卷积层分别采用ReLU 和Softplus 作为激活函数，两个全连接层分别采用Softplus 和ReLU 作为激活函数.通过实验数据可知，组合模型中，激活函数ReLU 使用最多，也证明的ReLU 函数具有更好的通用性.