基于模拟样本训练的支持向量机

张洪胜，高海宾

（淮南联合大学 计算机科学与技术系， 安徽 淮南232038）

随着网络技术应用的高速发展，互联网每天都产生着海量的网页、邮件等结构化和半结构化的文本信息，基于内容学习的文本分类技术是整理和获取文本信息的重要方式之一.在基于内容学习的文本分类过程中，特征选择是文本分类的关键步骤，人工标注的训练样本是影响特征选择质量的重要因素［1］.海量文本信息的分类，要求人工标注的训练样本必须具有一定的数量规模和广泛代表性，才能保证通过训练学习得到的分类模板具有较高的准确率和稳定性.传统的人工标注样本需要具备专业知识的人员才能完成，而标注大量的样本开销昂贵［2］，大规模、高质量的人工标注样本较难获得［3］，并且在将人工标注的普通样本转换为用于机器学习的样本时，存在着转换时间较长的问题.针对这种情况，笔者提出了一种利用有限人工标注样本特征空间的模拟样本生成算法，并将其用于并行支持向量机的文本分类中.实验表明，利用有限样本构造特征空间模拟生成的大规模训练样本，可以训练出具有良好分类效果的分类器，并且这种方式能够大大减少训练样本的生成时间.

1 支持向量机的文本分类

1.1 支持向量机分类原理

支持向量机（Support Vector Machine，简称SVM）是基于统计学习理论和结构风险最小化原则的一种分类方法，由于其很少过度拟合，适合解决训练样本少、特征维数高的文本分类问题［4］.

对于线性可分问题，假定训练数据（xl，yl），…，（xi，yi），xi∈Rn，yi∈{+1，-1}能够被超平面（w·x）-b=0 完成正确地分开，那么与两类样本点边缘最大的超平面具有最佳的分类能力.最优超平面将由离它最近的少数样本点决定，这些少数样本点称为支持向量.求最优超平面问题可以转化为一个凸二次规划的求解问题，即：

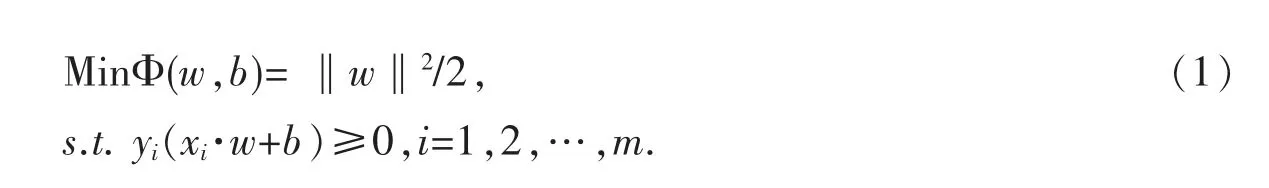
构造Lagrange 函数：

其中αi是Lagrange 乘子，根据Kuhn-Tucker 条件，αi满足消去w 和b，通过运算得到原最优化问题的Wolfe 对偶问题：

解出αi后，利用w=确定最优超平面，由此得到分类判别函数：

对于非线性可分数据，根据mercer 条件可以通过某种非线性变换K（xi，xj）=ø（xi）·ø（xj）映射到一高维空间，使它们在高维空间线性可分.此时的对偶问题为：

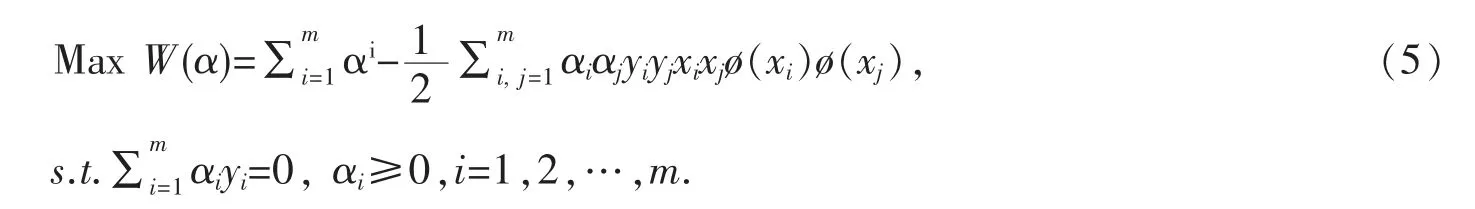
对应的分类判别函数为：

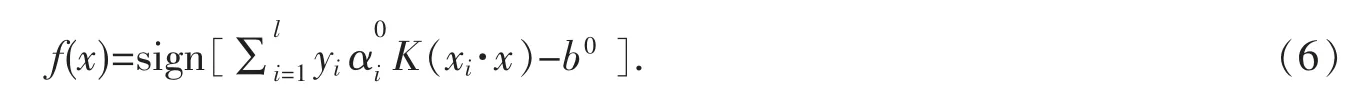
1.2 支持向量机的文本分类过程

以两类文本分类问题为例，基于内容学习的文本分类系统的训练和分类过程为：

（1）准备一定数量人工标注的正例训练样本和反例训练样本.

（2）对正例训练样本采用某种分词算法进行分词，通过特征抽取从中选取一定数量的词来表示类文本特征.可用于特征选择的评估函数有文本频数、信息增益、互信息、X2估计、文本证据权和优势率等［5］.抽取得到的所有特征在一起构成一个可以表示该类文本的n 维向量空间［6］，n 为抽取得到的该类文本特征的个数.

（3）将所有的训练样本分词，并按生成的特征空间表示为n 维空间的向量形式：（w1，w2，w3，…，wn），其中wi为通过某种方式计算得到的第i 个特征词的权重.权重的表示有相对词频和绝对词频两种方法［7］.绝对词频为词在文本中出现的次数表示， 相对词频采取如TF-IDF 等公式通过计算得到，TF-IDF 公式有多种，较为普遍的一种TF-IDF 公式，见公式（7）：

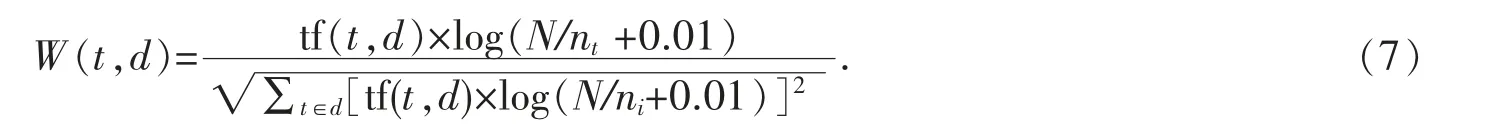
其中，W（t，d）为词t 在文本d 中的权重，而tf(t，d)为词t 在文本d 中的词频，N 为训练文本的总数，nt为训练文本集中出现t 的文本数，分母为归一化因子.

（4）通过某种机器学习算法，对向量形式的训练样本进行训练学习，得到分类器的分类模板.

（5）将待分类的文本分词，并根据特征空间同样表示成向量形式，然后用分类器及分类模板对其进行判断，得到分类类别.

2 训练样本的模拟生成

2.1 特征空间下训练样本的特点

正反例训练样本按照特征空间转换成向量形式的训练样本后，从直观上看，正例样本的所有非0 特征的权重值之和通常情况下应大于反例向量，而且权重值非0 的特征在正反例向量中出现的位置具有一定的随机性.

2.2 训练样本模拟生成算法

根据正反例样本的特点，我们利用向量特征空间和TF-IDF 特征权重计算方法，设计了一种训练样本模拟生成算法，算法步骤如下：

第1 步：准备一定数量的正例样本，对每个样本进行中英文分词并统计词频，并根据词频大小，按照一定比例如提取作为特征空间的特征，并做去重处理；

第2 步：按照TF-IDF 计算所有特征词的权重，为了得到特征词在正例所在类的权重，在计算时对公式（1）中tf(t，d)的定义做了修改，将其原来为词t 在文本d 中的词频，改为t 在所有正例样本中出现的词频；

第3 步：随机生成样本中非0 特征的个数m（1～10）；

第4 步：通过循环，随机生成m 个特征在特征空间的位置i，由此得到由m 个特征组成的、且特征出现位置随机的模拟样本；

第5 步：根据需要生成样本的个数，重复第3～4 步；

第6 步：对于生成的每个向量形式的模拟样本，计算各维的权重之和weightsum，若满足条件（weightsum＜阀值），则将该模拟样本作为反例样本，否则作为正例样本，由此得到用于训练学习的所有正反例样本，条件中的阀值可以通过分类效果比较实验进行确定.

2.3 模拟样本训练的支持向量机

利用模拟样本进行训练分类的支持向量机文本分类模型见图1.利用模拟样本训练和分类的支持向量机，其训练分类过程与文中1.2 节所述过程基本相同，但其训练样本不再是从人工标注的训练文本转换得到，而要利用2.2 节的模拟样本生成算法，根据需要随机生成获得.

图1 模拟样本训练的支持向量机文本分类模型

3 实验和结果

3.1 实验环境

实验以400 份人工标注训练样本为正例样本，通过特征抽取和TF-IDF 权重计算生成特征空间，抽取特征338 个.实验中人工标注样本使用的是NLP 文本分类语料库（复旦大学）中的训练与测试集.支持向量机采用Platt 提出的序列最小优化（Sequential Minimal Optimization，SMO）算法［7］.

3.2 实验及结果分析

（1）实验一：模拟样本生成及SVM 分类训练实验.按照笔者提出的模拟样本生成算法，以（样本非0特征权重之和＜阀值）作为反例生成条件，不满足条件的模拟样本作为正例样本，随机模拟生成共1 000个正反例训练样本， 测试样本全部为人工标注样本， 观察不同阀值情况下， 通过模拟样本训练得到的SVM 分类器的分类效果.由表1 可知，实验一的结果表明，随着非0 特征权重之和这个阀值的增大，生成的反例样本数量增加、正例样本数量数据减少，通过模拟样本训练得到的SVM 分类器的正确率也在随之发生变化，样本非0 特征权重之和设为＜1.0 的阀值时，生成的模拟样本训练效果较好，随着阀值的增大，反例样本生成过多，训练得到的分类器的分类效果下降.

表1 模拟样本生成及SVM 分类实验

（2）实验二：在具有不同特征维数的特征空间中，设置相同的阀值，利用模拟样本生成算法生成1 000个正反例样本，观察特征空间维数的变化对模拟样本生成的影响.由表2 可知，在模拟样本生成算法中的阀值相同的情况下，特征空间维数减少，反例样本生成数量呈减少趋势，特征空间维数增加，反例样本生成数量也相应增加.反例样本增加或减少到一定程度，都会导致分类器的分类效果下降，因此，针对不同的特征空间，需要选择合适的阀值，使模拟生成的正反例样本数量处于适当的比例，使训练得到的分类器具有较好的分类效果.

表2 特征空间维数对模拟样本生成训练的影响（权重和＜2.0）

（3）实验三：特征空间和阀值相同，多次执行同一算法，生成相同数量1 000 个的训练样本，观察算法中的随机过程对模拟样本训练分类效果的稳定性会否产生影响.由表3 可知，模拟样本生成算法中非0特征位置和非0 特征数量的生成具有一定的随机性，但在特征空间、阀值及样本生成总数确定的情况下，模拟样本的训练分类效果具有较好的稳定性.

表3 算法中的随机过程对训练分类稳定性的影响（权重和＜1.0）

（4）实验四：生成相同数量向量形式的训练样本，模拟样本生成和正常样本生成的时间和分类效果比较.由表4 可知，生成相同数量训练样本，模拟样本生成算法所需的时间远远低于正常方式生成训练样本的时间，生成样本数量规模大幅增加时，模拟算法生成样本时间增长不明显，并可能由于随机生成样本中非0 特征数量的减少而呈现训练时间反而减少的状况，而正常方式生成样本在样本规模增加时，样本生成时间则同向增长且增长显著.

表4 样本生成时间对比实验

4 结语

针对基于内容学习的文本分类方法在面对大规模文本分类问题时，人工标注的训练样本存在样本数量有限、获取困难等问题，根据特征空间下向量形式训练样本的特点.笔者提出了一种基于特征空间和TF-IDF 权重计算的模拟样本生成算法，并将其用于支持向量机的文本分类中.实验表明，相对于传统的训练样本转换方法，基于特征空间和TF-IDF 权重计算的模拟样本生成算法可以在较短时间内快速生成大规模的模拟训练样本，并且在支持向量机文本分类中表现出良好的性能，可以作为机器学习在人工标注样本数量不足情况下一个很好的补充.