基于混合神经网络模型预测下的统计套利研究

邓晓卫，章铖斌

（南京工业大学a.数理科学学院；b.海外教育学院，南京 211800）

0 引言

统计套利通过对历史数据进行统计分析，从一组资产的定价偏差中获利。价差的波动率决定了套利的成本和收益，而套利资产组合价格收敛是套利策略的基本保证。目前为止，国内外关于统计套利的研究，主要针对于各种期货产品的套利策略研究[1-4]。随着机器学习研究的深入，学者们发现建立在机器学习方法上的预测比一般时间序列的预测模型要更精准[5-8]。于是有学者将神经网络模型运用在统计套利中，如：徐颢华等[9]引入差分BP神经网络及拓扑结构对股指期货进行预测，检验其预测结果好于普通BP神经网络预测，提出可用于套利；靳朝翔等[10]以焦炭、铁矿石和螺纹钢为例，基于NAR动态神经网络模型研究套利策略；刘阳等[11]将神经网络模型与动态GARCH模型相结合，提出了一种基于信息更新NN-GARCH模型，对大连商品交易所的大豆一号和二号的统计套利策略进行了研究。

综上，关于统计套利的研究特点是：第一，在研究对象上，大部分以期货产品为主，且套利产品一般是基于两个产品进行；第二，在研究方法上，基本还是采用协整分析、误差修正模型等方法。虽然基于神经网络的统计套利有初步的研究，但研究的方法和对象还十分欠缺。如文献[9]提出的差分BP神经网络模型可用于套利但并未对此真正展开研究。而且，这些研究都是基于较为基础的神经网络模型。本文的创新点在于：第一，就交易对象而言，选择国内股票市场进行研究，并且考虑多元投资组合的统计套利策略；第二，基于LSTM和BP神经网络模型，提出一个混合神经网络模型，并应用Google公司开发的最新机器学习框架Tensorflow进行统计套利研究。

1 混合神经网络模型

BP神经网络是一种多层的前馈神经网络，从激励函数Sigmoid函数开始：

然后通过隐含层的输出、输出层的输出、误差的计算、权值的更新、偏置的更新等步骤进行迭代，最终得到较理想的结果。

LSTM（Long Short-Term Memory）是一种时间递归神经网络，由通过精心设计的称作“门”的结构来去除或增加信息到细胞状态的能力，他们包含一个Sigmoid神经网络层和一个Pointwise乘法操作。LSTM拥有三个门（遗忘门、输入门、输出门）来保护和控制细胞状态。LSTM神经网络模型经过众多学者和研究人员改进，目前已被广泛用于多个领域，如语言翻译、图像识别、预测疾病、点击率、股票等。

由于LSTM神经网络在处理和预测时间序列中间隔和延迟相对较长的数据、学习长期依赖信息方面具有优势，故本文拟将LSTM模型用于统计套利的前期预测。但在对该模型实际运用时发现，单纯运用LSTM神经网络模型做预测，预测区间的前段效果并不是十分理想。于是本文提出一种混合神经网络模型，即在LSTM神经网络模型基础上引入BP神经网络模型进行预测修正，使得预测值更精准，最终提高了统计套利结果。具体步骤如下：

首先，将所有数据集分为训练集、测试集和预测集，用LSTM神经网络模型进行训练、测试和预测，预测值记为yLSTM；然后，将原先的训练集和测试集的数据重新分为新的训练集、测试集和预测集，记为训练集1、测试集1和预测集1，重复LSTM神经网络预测步骤，得到预测集1与真实数据误差的时间序列；最后，对该时间序列进行BP神经网络学习，得到预测集的误差项的变化，记为εBP，以此对yLSTM不太稳定的前段进行修正，得最终预测值为：

式（2）即为一个混合神经网络模型。下文将通过实证检验该混合模型的预测精度高于单纯用BP预测的精度。

2 混合神经网络模型套利策略

首先，由长期协整关系选出可能进行套利的n个资产，设为x1t，x2t，…，xnt（此处亦表示各资产的收盘价）；采用文献[9]的方法，可得该资产组合t时刻的利润为：

其中，ut=x1t-α1x2t-α2x3t-…-αn-1xnt右端各系数通过最小二乘拟合来确定。在确定各资产权重αi后，采用本文提出的混合神经网络模型，按累积叠加的方式用xit的前t个值去预测第t+1个值，再得到预测的利润函数序列{proft}。

然后，对时间序列{proft}进一步分析，通过建立ARMA(p,q)模型，从中分离出随机扰动项εt（此为白噪声序列），本文的统计套利是通过对扰动项εt的预测值来设计套利策略。经过多次尝试，最后选择的是ARMA(1,1)模型如式（4）所示：

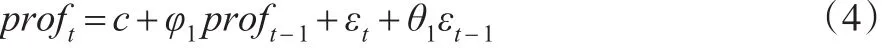
最后，统计套利最重要的是分析套利中出现的时机和概率。为此，本文先确立套利区间，使用上述模型计算得到残差εt，并且假设交易阈值为λ1和λ2，则λ1εt和 -λ1εt为交易（买空、卖空）的上下界。同时设立平仓的最大区域，设置λ2εt和 -λ2εt为平仓上下限。这里，λ1，λ2＞0 ，且λ2＞λ1。

建立套利的头寸后，当价差序列如期回归到μ±λi εt(i=1)区间时（μ为均值，此处为0）进行反向操作获利，从而完成一次正向或反向的套利。如果没有如期回归至标准差区间，本文设定了平仓上下限，即当价差触发μ±λiεt(i=2)以外的区域时，多头头寸或空头头寸立即平仓止损。该策略是基于风险管控的交易策略，为了避免过大的波动风险。

3 实证分析

3.1 数据选取及预处理

根据统计套利的相关理论，先找具有较高相关性的股票来作为研究样本。通过计算相关系数，本文选取了相关性较高的4只股票：中国银行、工商银行、农业银行和建设银行四大国有银行2016年1月1日至2017年9月30日每日开盘价、收盘价、最高价、最低价、复权价1、成交量、成交金额、振幅作为研究样本，用这8个变量使用混合神经网络模型对下一交易日的收盘价进行预测。数据来源于锐思金融数据库。混合神经网络模拟所用的程序基于TensorFlow框架，这是谷歌研发的第二代人工智能学习系统，并在2015年11月9日宣布开源，利用Python语言对此进行控制。统计软件使用Eviews10.0。

3.2 平稳性及协整检验

进行套利的组合产品需要满足协整关系。首先，对样本数据进行平稳性检验以确定他们的单整阶数。此处采用ADF检验。记x1t、x2t、x3t、x4t为工商银行、建设银行、农业银行、中国银行第t天的股票收盘价价格。对4只股票的收盘价及收盘价差分序列作ADF检验，结果显示①限于篇幅，此处省略了ADF的全部检验结果。：四家银行股票收盘价格序列均不平稳，但其一阶差分序列在1%的水平下均是平稳序列，即他们具有相同的单整阶数：{xit}～I(1)，i=1，2，3，4 。

其次，用E-G两步法对x1t、x2t、x3t、x4t进行协整关系检验。同时为了分析不同投资组合及不同神经网络模型在统计套利中的获利差异及优劣，本文以所选的4只股票为基础构造了四种投资组合（见表1），分别对他们进行协整检验。

表1 投资组合列表

先对Porti，(i=1，2，3，4)进行OLS回归，以获取残差项uit，i=1，2，3，4 。再对该残差序列分别进行单位根检验，结果如表2所示。

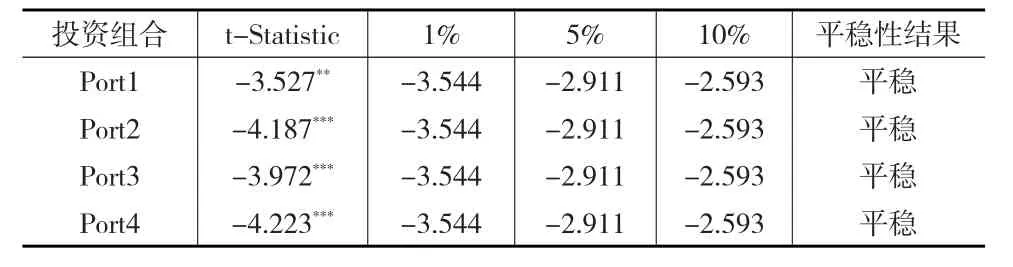
表2 uit的单位根检验结果

结果显示，四组残差序列在1%或5%的置信水平下均平稳，从而所构造的四个组合均存在长期的协整关系。

3.3 套利策略制定

根据式（3）定义，该四种组合的套利收益可以表示为：其中，uit，t=1，2，3，4 。由前OLS回归结果确定，具体如下：

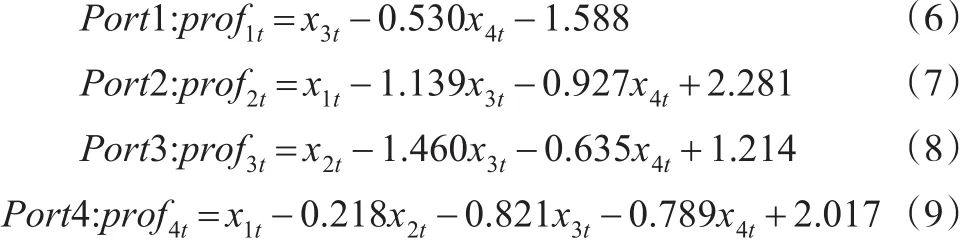
对每只股票将其样本数据分为训练集：2016.01.04-2017.04.05；测试集:2017.04.06-2017.07.06及预测集：2017.7.7-2017.9.29。运用混合神经网络模型按前述给定的策略进行训练、测试及预测。实验中设定训练次数为10000次，学习速率为0.0006，隐藏层为10层。通过上述训练、测试，预测出2017年7月7日至2017年9月29日的各股票价格走势，如图1所示。

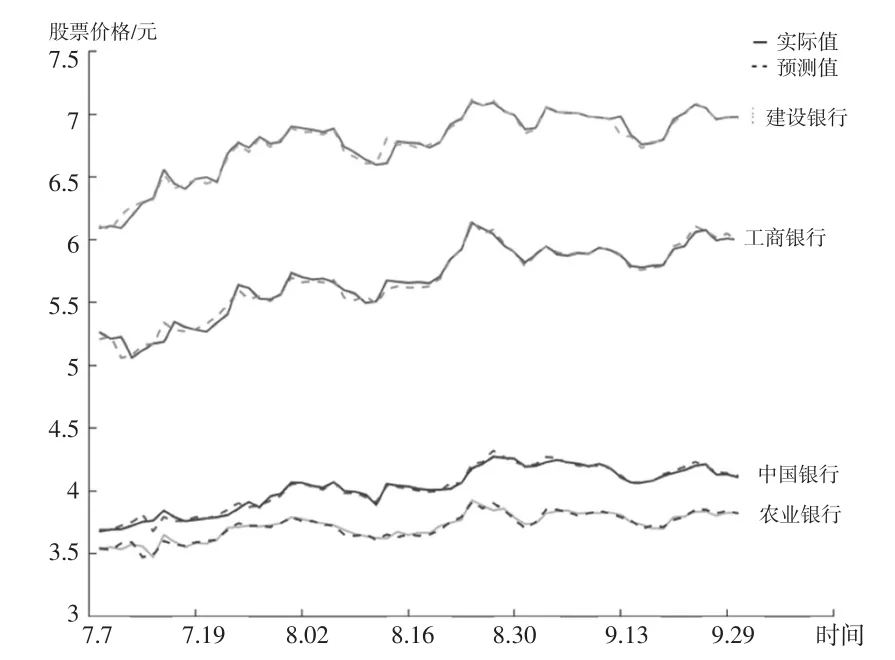
图1混合神经网络预测曲线与真实走势曲线比较图

再由式（6）至式（9）根据投资组合中各产品的权重计算出相应组合的利润序列值profit。

在得到利润序列{profit}后，建立其ARMA(1,1)模型，得到残差项εit，之后按设定套利和平仓阈值并进行套利，由此完成统计套利的全过程。

具体交易策略。如对投资组合1即Port1，由式（6）：一份完整的多头头寸交易是买入0.53份中国银行股票同时卖出1份农业银行股票；一份完整的空头头寸交易则是卖出0.530份中国银行股票同时买入1份农业银行股票。同理，Port2、Port3和Port4中，各金融产品的投资比例由式（7）至式（9）确定，分别为：1∶-1.139;-0.927;1∶-1.460∶-0.635以及1∶-0.218∶-0.821∶-0.789。

其中，“-”代表反向操作，当然真正购买股票不存在小数，但这不影响交易策略的制定，因为可以同比例放大，使得交易比例为整数即可实现真正的套利方案。

3.4 套利交易结果

为比较BP、LSTM以及混合神经网络模型预测套利的优劣，先采用BP神经网络进行预测，发现预测平均误差超过1%；然后采用LSTM神经网络进行预测，预测平均误差降低到0.7%左右；最后用混合神经网络预测，平均误差在0.5%左右。表3给出了基于BP神经网络和混合神经网络预测并进行套利结果（鉴于LSTM只在预测区间的前端误差较大，总体套利结果只在前段与混合神经网络模型套利结果出现差异，故此处省略）。

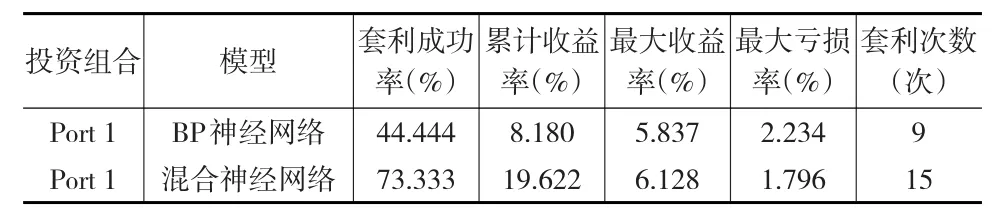
表3 Port1投资组合套利结果

从表3中可以发现，无论是从套利成功率、累计收益率、最大收益率，还是从最大亏损率和套利次数来看，混合神经网络模型的套利结果均优于BP神经网络模型的套利结果。由此可见，预测准确率是统计套利成功的重要保证。预测越准确，套利成功率、收益率和套利次数越高，同时最大亏损率下降，说明提高预测准确率可以显著减少风险。

接下来本文探讨在原有两个组合中增加投资组合产品个数，再应用混合神经网络模型和BP神经网络模型进行统计套利会产生什么样的结果。仍旧从套利成功率、累计收益率、最大收益率、最大亏损率和套利次数这几个指标研究套利策略效果，结果见表4。

表4 投资组合Port2—Port4的两种模型套利结果比较

结合表4和表3可以得到：本文提出的混合神经网络模型的套利成功率及累计收益率均高于单一BP神经网络模型的套利结果；增加投资组合中的产品数，即投资组合的多元化可以有效地增加套利成功率和累计收益率；基于混合神经网络模型的最大亏损率低于单一BP神经网络模型套利的最大亏损率。但从Port2—Port4的结果发现：基于混合神经网络模型预测成功的套利次数与基于BP神经网络模型预测成功的套利次数没有显著提高（但亦没有减少）；特别是最大收益率指标，有的组合（如Port3）混合预测的结果低于BP神经网络模型预测的结果。具体分析其原因发现：套利结果的好坏与投资组合中金融产品本身的优劣有较大的关系。事实上，Port2是在Port1的基础上增加了工商银行；Port3是在Port1的基础上增加了建设银行，经过查证，在此预测时间段内，工商银行主营收入增长远高于建设银行。由此可见，在投资组合中增加产品，要审慎选择。增加产品的好坏可能直接影响到统计套利的成功及获利大小。怎样审慎选择一个投资组合？这正是下一步研究的问题。

4 结论

本文以LSTM神经网络模型和BP神经网络模型为基础，提出了一个混合神经网络模型，用于统计套利的预测，研究不同的投资组合下的统计套利策略，并用中、工、农、建四大国有银行2016年1月1日至2017年9月30日的真实数据为样本进行实证分析。结果显示：本文提出的混合神经网络模型的预测准确率明显高于BP神经网络的预测结果。带来的直接效果就是使得套利收益率显著提升，即采用本文提出的混合神经网络的套利策略是十分有效的。不仅如此，混合神经网络的套利成功率、套利次数均增加，最大收益率和最大亏损率均得到改善，因此采用混合神经网络建立预测模型,并进行套利,会使预测更准确，套利更精准，收益也更大。之后投资组合的多元化检验，不仅同样符合上述结论，也可以有效地增加套利次数和套利成功率，说明投资组合越多元，相对风险会更小，换言之套利机会越多。但并不是投资组合中的金融产品越多越好，只有对金融产品作合理筛选，包括数量和质量，才能获得较好的投资收益。

研究中也存在不足，首先本文只选择了四个公司做样本进行研究，样本较少可能存在一定的实验误差。其次，在统计套利收益的测算中，没有考虑交易所产生的费用，如手续费等。当考虑相关费用，投资收益会有所下降，但是对整体实验结果无较大影响。再次，以什么原则选择一组投资组合产品，以获得更多套利机会和更高收益？本文还没有给出确定的方法。