贫富差距与房价走势关系的实证检验

郑 军，胡 蓉

（1.广东财经大学 金融学院，广州 510320；2.广东金融学院 应用数学系，广州 510521）

0 引言

市场化以来，我国房价普遍飙升。房价高企不仅增加了中低收入居民的消费性购房压力，而且加剧了整个宏观经济的运行风险。与此同时，由于我国制度不完善等原因，宏观经济增长的硕果并没有惠及大多数居民，而是被少数占有特定资源和权利的阶层攫取，进而扩大了居民之间的财富差异。当社会总财富分配不均等程度加剧时，一方面压缩了当前房屋的消费需求且扩大了未来房屋的消费需求；另一方面更富有的居民将有能力进行房地产投资，以期从未来房屋价值增值中获得收益。Chen等（2010）[1]的研究表明，我国居民的资产70%以房地产形式持有，房地产是我国居民热衷追捧的资产，而房地产投资属性的凸显扩大了社会总财富分配的不均等程度，进而推高了房地产市场价格。因此，贫富差距是决定房地产市场价格水平的重要因素。

Määttänen和Tervio（2014）[2]通过构建静态纯交换经济中的指派模型首次分析了收入分配与房价之间的关系。在他们的模型中，由于假定每个经济参与者拥有单位数量的房屋，从而得出在平均意义上收入分配不均等程度增加导致房价下跌的结论。然而，社会中每户居民拥有单位数量房屋的前提假设与我国现实情况并不相符，因此Määttänen和Tervio（2014）[2]的结论在我国房地产市场中是否成立有待考究。郑军等（2014）[3]结合文献[2]和文献[4]的研究思想，基于CCAPM框架构建了财富不平等与房价关系的理论模型，认为财富不均等程度是导致我国房价攀升的重要动因。李仲飞等（2016）[5]在区分不同经济发展水平前提下实证分析了收入差距与房价变动趋势之间的相关性。而本文实证研究的理论基础则是郑军等（2014）[3]构建的CCAPM理论模型，实证结果证实了他们的理论预测。

1 均衡房价基本模型

由于房屋兼具消费和投资的双重属性，且房屋占据我国居民财富的很大比例，因此贫富差距与房价间存在很强的相关关系。考虑一个具有两类经济代理人（或称为居民，分别用类型1和类型2表示）的纯交换经济，每种类型的代理人都包含无数个个体，从而经济中的单个代理人无法左右市场价格（市场是完全竞争的）。每个代理人赋予两状态随机禀赋流（或收入流），其中，yt∈为代理人的最长生命期。进一步假定禀赋流过程是风险率（hazard rate）为κ（κ＞0）的Poisson过程，禀赋从t时刻的状态yd（yu）转移到t+δt时刻（δt＞0为非常小的时间区间）的状态yu（yd）的概率为，因此，从时刻t到时刻t+δt，居民的禀赋不发生变化的概率为假定两类代理人的禀赋完全负相关。为集中考察总财富不平等对房价的影响，假定在时刻t∈[0 ，T)经济中的总禀赋为常数1，在生命期结束的T时刻禀赋为零。代理人消费房屋（ht）与其他消费品（nt）。在[0 ，T)期间经济中存在供给固定为1的房屋资产（不考虑经济中的生产，房屋资产外生给定），房屋资产在代理人生命期末的T时刻一次性报废（残余价值为零）；代理人持有房屋资产可获得固定的房租流r（以其他消费品作为度量单位），0＜r＜1；假定t期房屋（以其他消费品计价）价格为Pt。t期类型1代表性代理人的房屋资产头寸为，类型2代表性居民的房屋资产头寸为。假定在时刻t∈[0 ，T) 类型1与类型2的代表性居民的房屋资产头寸分别满足为融资约束界。假定在初始0时刻经济处于均衡状态，因此，类型1代表性代理人与类型1代理人整体的房屋资产持有比例相等，即由于房屋资产在代理人生命期末一次性报废，因此可认为代理人在生命期结束的T时刻房屋资产头寸持有量为零。假定t时刻类型1代表性代理人的禀赋（流量）为yt，则类型2代表性代理人的（可支配）禀赋应为1-r-yt。假定所有代理人具有相同的偏好，用效用函数表示为：

其中，θ为t时刻代理人在其他消费品上的支出份额，σ为跨期替代弹性。当σ较小时，代理人消费的跨期转移意愿较弱。

代理人在生命期[0 ，T)内的任何时刻都消费房屋和其他消费品，并购买房产（作为对不确定性禀赋的保险）。房屋消费由房屋出租市场中的价格（房租）决定。代理人在t时刻的总收入由“时间段[t-δt，t] 上的累积禀赋（流量）加上t-δt时刻买进的房屋资产（存量）在t时刻所获得的总收益”组成。因此类型1代表性代理人的跨期预算约束可表示为：

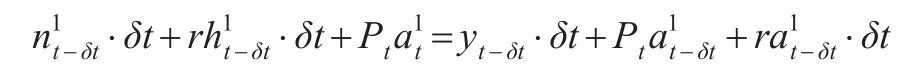
假定类型1代表性代理人的房屋资产头寸是时间t的连续函数，令表示类型1代表性代理人的房屋资产头寸变化率，则类型1代表性代理人的房屋资产头寸运动方程可表示为：

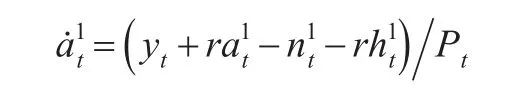
同理，类型2代表性代理人的跨期预算约束为：

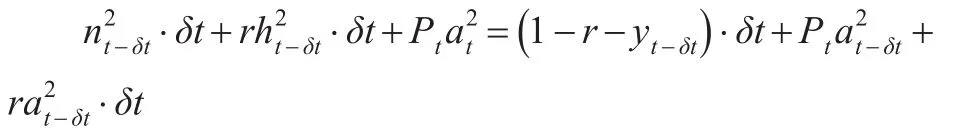
在上述模型设置下，郑军等（2014）[3]通过动态优化方法获得了房地产市场均衡满足的偏微分方程组。数值模拟结果表明：在禀赋分配给定的情形下，两种消费品的消费均随着房屋资产财富分配的不均等程度增加而增加；在给定房屋资产财富分配均等程度的情形下，禀赋高的居民的消费高于禀赋低居民的消费。下面利用我国房地产市场以及宏观经济相关数据验证上述理论结果的可靠性。

2 变量选取与数据说明

根据研究问题的着眼点与数据可获得性的要求，本文选取1993—2015年全国商品房销售价格（用HPRICE表示）的年度数据代表房地产价格的变化；选取1993—2015年全国人均GDP（用PGDP表示）的年度数据代表宏观经济的变化，用其作为本文构建的计量模型的控制变量；选取1993—2015年全国基尼系数（用GINI表示）的年度值代表我国居民收入与财富的分配情况①全国商品房年销售价格数据来源于中国房地产行业研究数据库（http：//www.gtarsc.com/）；全国人均GDP数据来源于国家统计局网站（http：//www.stats.gov.cn/）；基尼系数来源于国家统计局最新公布的数据，并按照相同的方法自行计算得出1993—2002年的数据。。为了控制可能存在的异方差问题，本文对全国商品房销售价格和全国人均GDP取对数。数据的描述性统计如表1所示。

表1 数据的描述性统计

为避免出现“伪回归”，在对模型进行回归分析之前需检验变量的平稳性。本文采用ADF对各变量进行单位根检验，检验结果列于表2。由表2可知：当对各时间序列的水平值进行ADF检验时，结果表明均不能拒绝“存在单位根”的原假设；然而当对变量进行一阶差分后进行ADF检验，检验结果显著地拒绝“存在单位根”的原假设。由此得出结论，各个时间序列均为非平稳的I(1)过程。

表2 ADF单位根检验

3 实证结果与分析

鉴于实证分析为验证理论分析结论的可靠性，本文将基于数据的统计性质建立计量模型。Sims（1980）[6]引入的VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数，从而较好地解决了内生性问题，为预测相互联系的时间序列系统以及分析各种经济冲击对经济变量的影响提供了研究思路，从而在经济系统动态性实证研究中得以广泛应用。

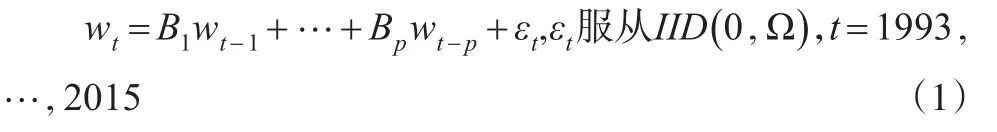
式（1）中p为最优滞后阶数，B1，…，Bp为 3×3的系数矩阵，εt为3维扰动向量，他们相互之间可以同期相关，但不与自己的滞后值以及内生变量的滞后值相关，Ω为3×3维协方差矩阵。

首先，要获得上述VAR方程（1）的确切形式，需要确定模型的最优滞后阶数p。如果p太小，误差项的自相关有时很严重，从而导致被估计系数不满足一致性；如果p太大，将导致自由度减小，从而影响被估计参数的有效性。本文根据Neyman-Pearsond的似然比（LR）统计量确定最大滞后阶数p。根据此方法，可知p=2是可行的。

图1 AR模型特征根的倒数分布图

3.1 协整检验

上述检验已给出各个时间序列均为非平稳的I(1)过程，现在通过协整检验各变量的组合是否存在长期均衡关系。检验结果如表3所示，可以看出，房价、基尼系数与人均GDP之间存在协整关系。

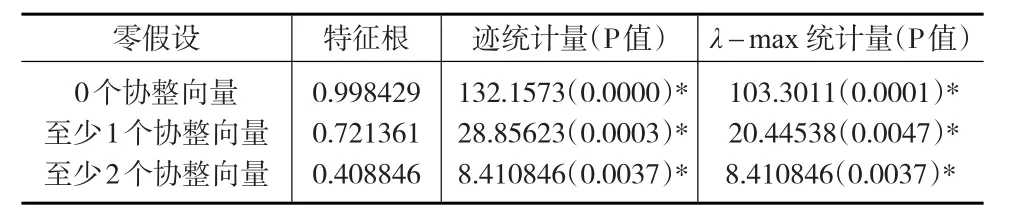
表3 协整检验结果

3.2 Granger因果关系检验

基于上述准备，现在探究各变量之间的因果关系，本文采用Granger因果关系检验法。Granger因果关系检验实质上是检验一个变量的滞后变量是否可引入到其他变量的方程中。一个变量如果受到其他变量滞后值的影响，则称他们具有Granger因果关系。选取最优滞后阶数为2阶，检验结果列于表4。

从上述检验可得结论：当最优滞后期数选择为2时，拒绝“基尼系数不是房价的Granger原因”犯错概率为2.43%，但拒绝“房价不是基尼系数的Granger原因”犯错概率高达50.46%，因此，拒绝基尼系数不是房价的Granger原因的零假设而接受房价不是基尼系数的Granger原因的零假设。这一实证结论与理论结果完全吻合。同理也可以得出人均GDP是房价的Granger原因而房价不是人均GDP的Granger原因的结论。因此，在其他因素给定的情况下，房价的正常上涨由经济增长决定，换言之，当社会总财富分配较为均等且抵押融资的杠杆效应处于合理水平时，房价的增长主要由经济增长决定。另外，本文的检验也给出了基尼系数与人均GDP之间的因果关系，GINI是人均GDP的Granger原因；反之则不然。这为我国改革过程中一直采用的“试点”改革的策略方针提供了理论支持。

表4 Granger因果关系检验

3.3 脉冲响应分析

VAR模型是一种无需对变量作任何先验性约束的非理论性模型。因此，在分析VAR模型时，往往不分析一个变量的变化对另一个变量的影响如何，转而分析模型受到某种冲击时对系统造成的动态影响，即脉冲响应分析[7]。下面通过给一单位大小的内生变量冲击得到房价的脉冲响应函数图,如图2至图4所示。图中横轴表示冲击滞后的期数（单位：年），纵轴表示房屋价格（单位：元）。

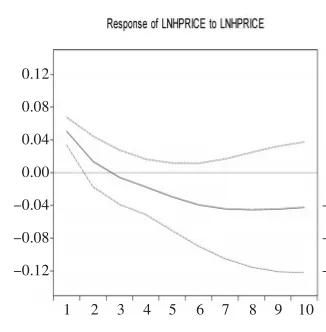
图2房价冲击对 自身的影响

图3基尼系数冲击对 房价的影响

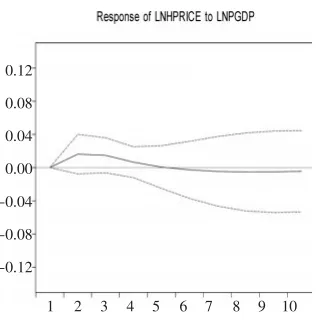
图4人均GDP冲击对 房价的影响

图2为房价冲击对自身的脉冲响应函数图。当期一单位房价的正冲击对下一期房价影响最大，为0.05，随着时间推移这种冲击的影响越来越小，到第3期影响变为-0.005，之后负的影响越来越大，大约到第7期这种负的影响才会趋于稳定。这表明房价正的冲击对自身的具有负的持续效应。图3反映了基尼系数冲击对房价的脉冲响应。从图中可以看出，当期基尼系数正的冲击后，其对房价的影响在前几期持续增加，到第7期达到最大值0.048，之后这种影响以相对缓慢的速率递减。图4反映了人均GDP冲击对房价的脉冲响应。从图中可以看出，当期人均GDP的正冲击在前5期对房价有正的影响，然而第5期之后这种影响变为相对稳定的负数。因此可得出结论：从冲击的持续效应来看，基尼系数正冲击对房价具有较长时期的正持续效应，而房价与人均GDP的正向冲击对房价的正向影响持续期较短。这或许可从预期理论以及耐用品需求理论得以解释：一方面，当房价突然上涨时，居民预期未来房价将继续上涨，于是在接下来的年份居民加快入市的步伐从而推高了房价；另一方面，由于房屋的耐用性，需求的提前实现掏空了接下来的年份的市场需求，从而致使这种正向冲击效应反向。

3.4 方差分解

脉冲响应给出了系统对一个内生变量冲击的效果，但并未提供各变量冲击贡献的大小。下面利用方差分解获得各变量冲击对系统的均方误差所做的贡献。图5至图7给出了各内生变量变化对房价的方差分解图，其中横轴表示滞后期数（单位：年），纵轴表示内生变量冲击对房价的贡献率（单位：%）。

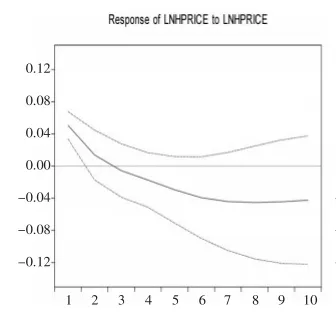
图5房价冲击对自身的贡献率

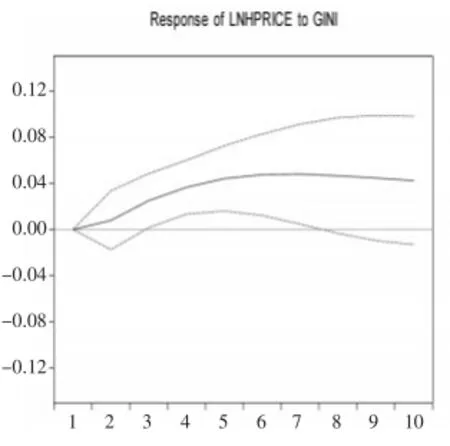
图6基尼系数冲击对房价的贡献率

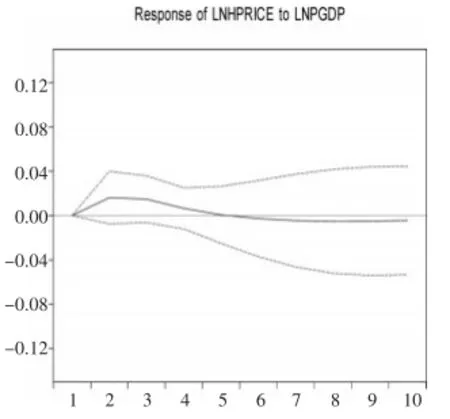
图7人均GDP冲击对 房价的贡献率

从图5至图7可以看出：基尼系数冲击对房价的贡献率最大，在50%左右，其次是房价自身冲击的贡献率在40%左右，人均GDP冲击对房价的贡献率较小，仅为5%左右。基尼系数冲击对房价的贡献率最大，这是由贫富差距扩大加剧了房屋从消费属性向投资属性转变所致。房价自身冲击的贡献率较高，可从预期理论得以解释。当前房价上涨使得居民看涨房地产市场价格，从而加紧入市推高了房价。人均GDP对房价的贡献率大小表明，在经济发展过程中，房价虽然也将随之上涨，但是经济发展对房价的推动作用并不大。

已有的理论与实证研究都表明，如果房价上涨仅仅是由于经济发展所致，那么房地产市场不存在风险，也不可能形成房地产市场泡沫。然而，过往的房地产市场泡沫破灭引发的经济危机的例子表明，房价上涨不仅仅是经济发展所致，更为重要的是市场参与者的财富分配状况以及其对未来房价的预期推高了房地产市场价格。因此得出结论，我国当前房价高企的主要原因是居民贫富差距较大，这再次证实了前文的理论结果。

4 结论

本文利用我国实际数据实证检验了我国房价攀升过程中居民贫富差距的作用。结果表明，贫富差距是导致我国房价高企的重要因素。这不仅为近年来政府出台的一系列房地产市场调控政策收效甚微提供了一种令人信服的解释，而且为政府将来制定房地产价格调控政策提供了指导方针。根据本文结论，贫富差距扩大将导致富裕阶层增加房屋资产投资，并以其作为对未来收入不确定性的保险。也就是说，贫富差距加剧将导致投资性购房增加，从而致使房屋从消费属性向投资属性转变，推高房价。与此同时，高房价增加了富裕阶层的房屋资产性收益，这又将进一步加大贫富差距，从而使得房价继续攀升，最终为整个宏观经济的运行带来显著的系统性风险。要将我国房地产市场的这种风险控制在不引发经济危机的范围内，政府需尽力将经济增长带来的社会总财富在居民间均等分配，从而将房地产市场中的投资性热情控制在适度范围，以避免过大的贫富差距催生房地产投资热情高涨而推高房价。