基于接近性综合关联度的区间灰数的决策模型
席沙沙,魏 勇
(西华师范大学 数学与信息学院,四川 南充 637000)
0 引言
灰色关联决策是灰色系统理论的重要组成部分,广泛应用于社会、经济的各个领域中。近年来,很多学者从不同的角度研究了多指标决策问题,取得了很大发展。对于具有区间灰数的多指标决策问题文献[1]提出了灰色区间关联系数公式,将经典灰色关联决策由清晰数的情况推广到了区间灰数的情况,建立了基于满意度水平下的灰色区间关联算法;文献[2]提出了基于理想方案的最大关联度方法、基于临界方案的最小关联度方法,以及同时考虑理想方案和临界方案的综合关联度方法;文献[3]提出了基于信息还原算子的区间灰数序列关联度的计算方法,研究了具有区间灰数的多指标决策问题,建立了多指标区间灰数关联决策模型;文献[4]提出了区间灰数关联决策方法,从而把灰色关联分析理论由实数序列拓广到区间数序列;文献[5]通过引进区间数向量范数,对区间数多指标决策问题的决策矩阵进行规范化处理,在此基础上给出了区间数多指标决策问题的灰关联分析法;文献[6]针对只有部分属性权重信息且属性值以区间数形成给出的不确定多属性决策问题,提出了一种逼近理想关联度的决策分析方法;文献[7]提出了一种基于灰色关联的区间评价方法;文献[8]探讨了决策方案的属性值为区间灰数、属性权重部分已知和决策者对方案有偏好的灰色决策问题。
文献[9]利用信息分解法将区间灰数序列分解成两个部分:一个为由区间左端点组成的“白部序列”,另一个为由区间长度组成的“灰部序列”。然后根据向量投影方法对正、负理想点的“白部”、“灰部”分别进行向量双向投影,进而根据构建向量双向投影的一次性决策模型。但是向量双向投影的方法计算复杂,因此本文对文献[9]的方法进行简化:在区间灰数序列信息分解的基础上,结合文献[10]中的接近性关联度,计算各区间灰数序列的“白部序列”、“灰部序列”与理想序列的接近性关联度,最后通过比较接近性关联度得出最好的方案。
1 基本概念与基本理论
定义1[11]:在灰色系统理论中,人们通常把只知道取值范围而不知道其确切值的数称为灰数。把既有下界aL又有上界aU的灰数称为区间灰数,记为
通常,在多属性决策中,有“效益型”属性、“成本型”属性等,且属性不同的“量纲”也不同,因此需要把不同属性的进行规范化处理,处理方法如下:
对于效益型序列,其区间灰数左右端点为:
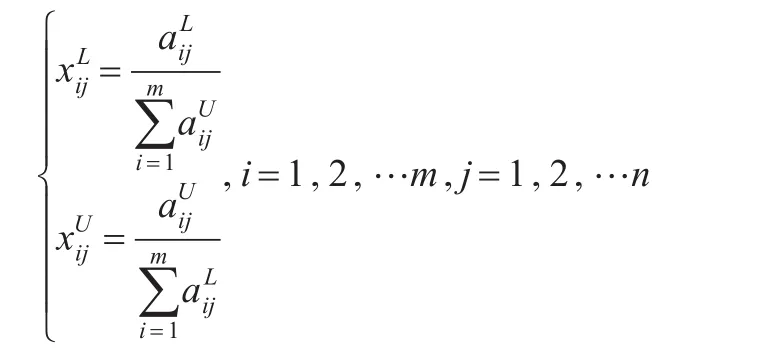
对于成本型序列,其区间灰数左右端点为:
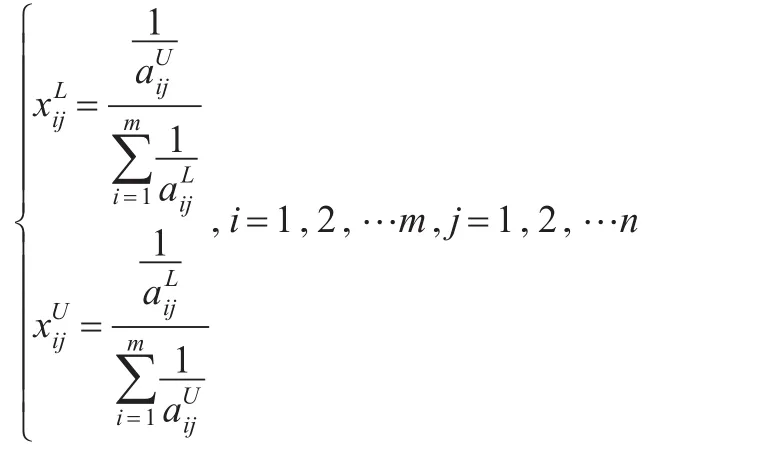
定义2[9]:设区间灰数序列为:
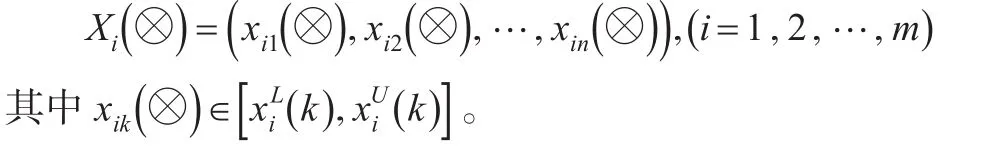

方案Xi与X+的“白部序列”的接近性关联度为:
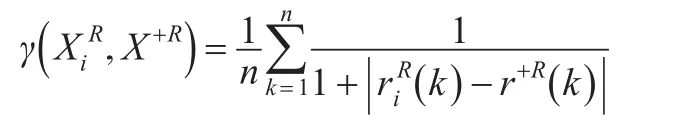
同理,方案Xi与X+的“灰部序列”的接近性关联度为:
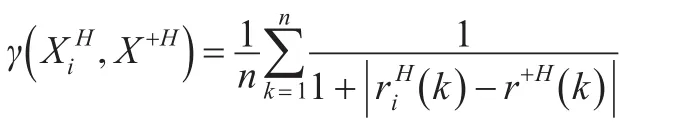
因此,方案Xi与X+的接近性综合关联度为:
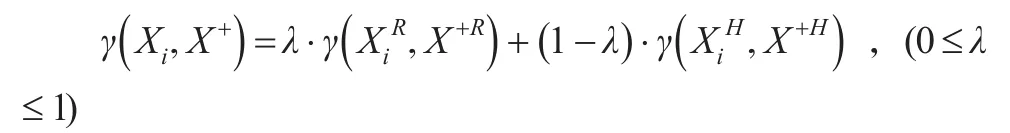
其中,权重一般取λ=0.5,当然也可根据具体情况斟酌确定λ。
对于在有部分权重信息的属性值为区间灰数的情况下,接近性关联度计算方法如下:

同理,方案Xi与X+的“灰部序列”的接近性关联度为:
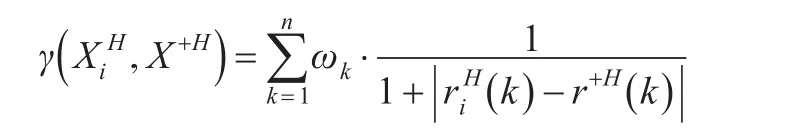
因此,方案Xi与X+的接近性综合关联度为:
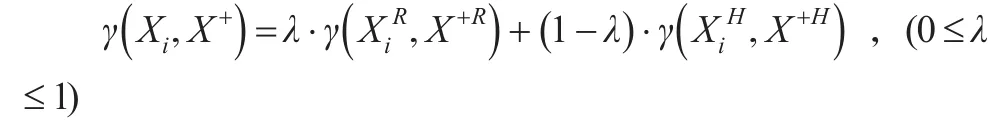
其中,权重一般取λ=0.5,当然也可根据具体情况斟酌确定λ。
2 算法步骤
第1步:构建区间灰数决策矩阵。
第2步:对区间灰数决策矩阵进行规范化处理。
第3步:构建理想方案。
第4步:利用信息分解法处理区间灰数。
第5步:计算各方案到理想方案的接近性综合关联度。(一般先分别计算各方案白部到理想方案白部的接近性综合关联度,灰部到理想方案灰部的接近性关联度,再计算各方案到理想方案的接近性综合关联度)。
第6步:根据接近性关联度进行方案排序。
3 应用实例
例1[9]:一家投资银行打算投资一个项目,现有4家公司X1、X2、X3、X4较为合适。现选取投资净产值率A1、投资利税率A2、内部收益率A3、环境污染程度A4这4项指标对这4家公司进行评估,来确定最终决定是否进行投资。具体数据如表1所示:其中A1、A2、A3为效益型指标,A4为成本型指标。
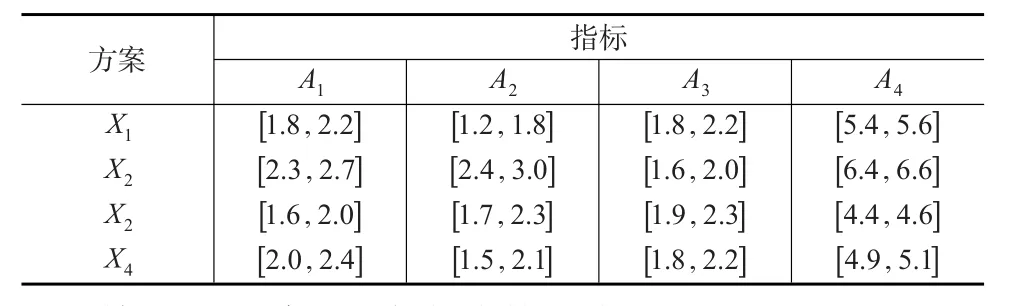
表1 区间灰数决策矩阵
第1步:构建区间灰数决策矩阵。
第2步:对区间灰数决策矩阵进行规范化处理(见表2)。
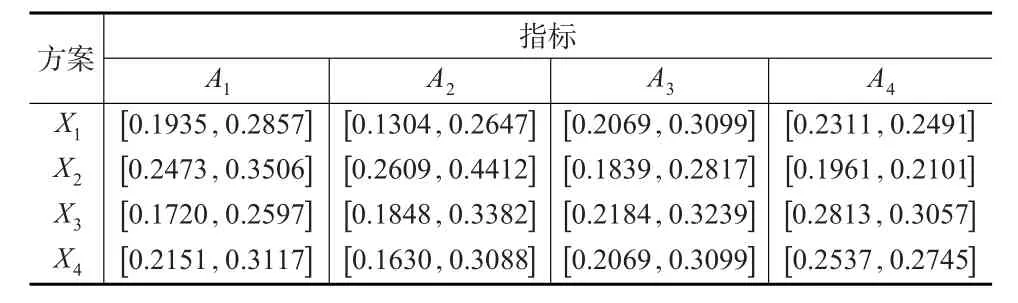
表2 规范化区间灰数决策矩阵
第3步:构建理想方案。
理想方案:
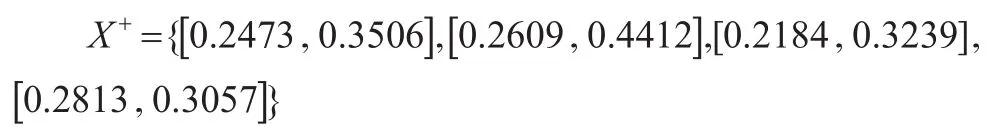
第4步:利用信息分解法处理区间灰数。
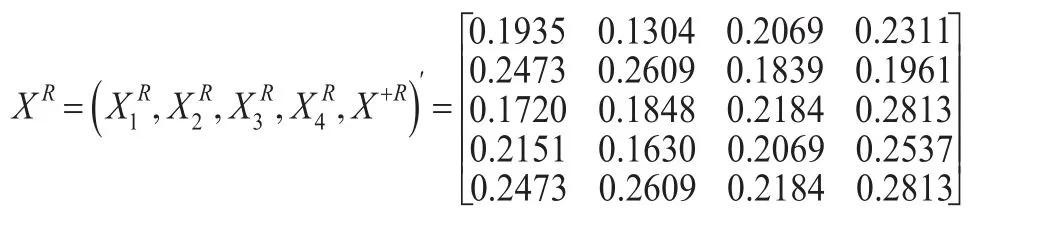
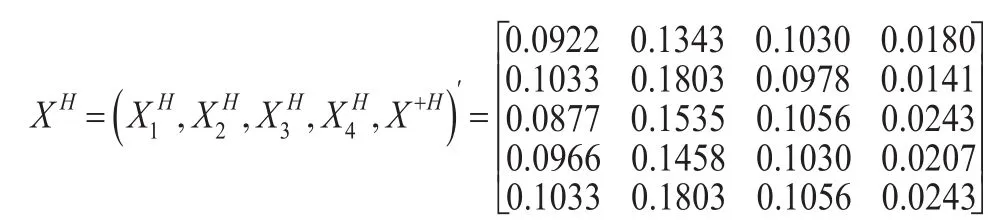
第5步:计算各方案到理想方案的接近性综合关联度。
接近性综合关联度又分三步完成:
①各方案与理想方案的“白部序列”的接近性关联度:
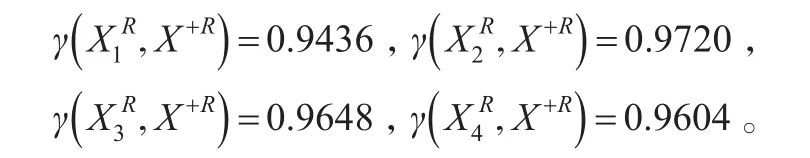
②各方案与理想方案的“灰部序列”的接近性关联度:
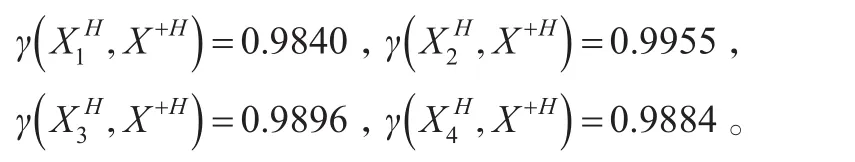
③各方案与理想方案的接近性综合关联度:对本例特殊情况而言各方案的“白部序列”与理想方案的“白部序列”接近程度,完全与各方案的“灰部序列”与理想方案的“灰部序列”接近程度排序一致,无论权重为何值,其综合关联度都会保持共同顺序,所以没有必要计算接近性综合关联度具体值,而直接进入下一步。
第6步:根据接近性关联度进行方案排序。
而文献[9]方案之间的排序也为X2>X3>X4>X1,显然本文的方法更简单。文献[9]运用了向量双向投影的方法来构建模型,计算过程复杂;而本文考虑到越接近理想方案则方案越好,从而选用了灰色接近性关联度来建模,且计算方法简单。
例2[2]:某人打算购买一套房子,现有4类房屋X1、X2、X3、X4可供选择。现选取房屋面积A1(m2);设备A2(水平);环境A3(水平);价格A4(单位面积价格:元/m2);距工作地点距离A5(公里)这5项指标对这4类房屋进行评估,来确定最终决定购买哪套房屋。具体数据如表3所示,其中A1、A2、A3为效益型指标,A4、A5为成本型指标。各指标权重为ω1=0.2087,ω2=0.2225,ω3=0.2256,ω4=0.2046,ω5=0.1386。
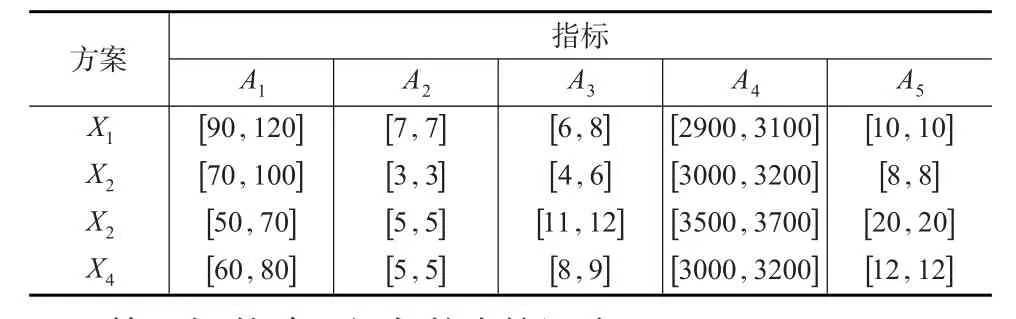
表3 区间灰数决策矩阵
第1步:构建区间灰数决策矩阵。
第2步:对区间灰数决策矩阵进行规范化处理(见表4)。
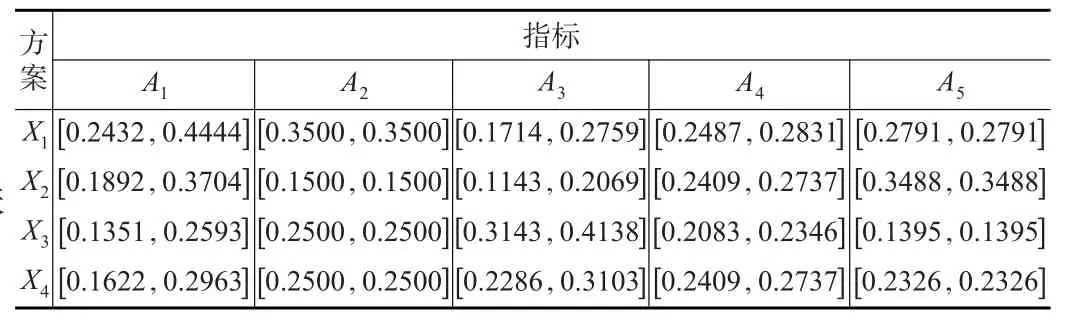
表4 规范化区间灰数决策矩阵
第3步:构建理想方案。
理想方案:

第4步:利用信息分解法处理区间灰数。

第5步:计算各方案到理想方案的接近性综合关联度。
接近性综合关联度又分三步完成:
①各方案与理想方案的“白部序列”的接近性关联度:
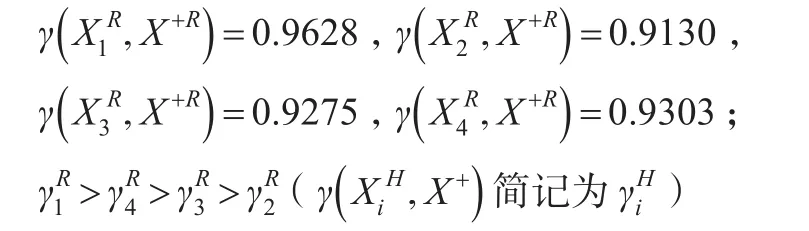
②各方案与理想方案的“灰部序列”的接近性关联度:
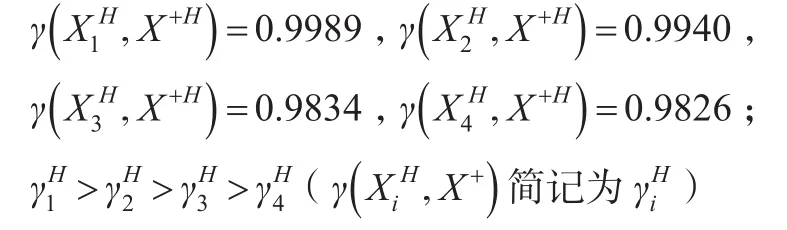
③各方案与理想方案的接近性综合关联度:
其实仅就寻找最优方案而言,无论是白部还是灰部都是方案是最接近,但方案2、3、4的排序差异较大,必须用综合关联度来权衡。
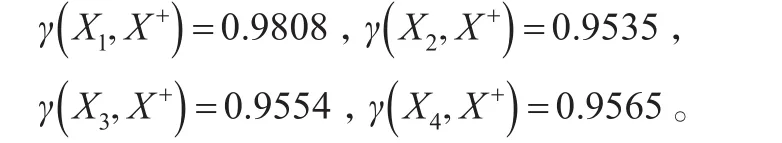
第6步:根据接近性综合关联度进行方案排序。
从计算结果上看出γ>γ>γ>γ(γ(X,X+)简记为
1432i γi)可知方案X1更接近理想方案,故方案之间的排序为X1>X4>X3>X2,因此购买第X1套房子较好。
而文献[2]方案之间的排序为X1>X4>X2>X3,也是方案X1较好。文献[2]同时考虑了理想方案和临界方案的综合关联度方法。而本文考虑了理想方案的接近性关联度的方法,显然本文的方法更简单。
4 结论
本文研究了决策矩阵为区间灰数的多目标决策问题,提出了将区间灰数序列分解为“白部序列”、“灰部序列”,然后分别计算出各方案与理想方案的“白部序列”、“灰部序列”的灰色接近性关联度。
该方法计算简便,具体体现在:
(1)对原始数据不作始点零象化、初值单位化、均值化等处理。避免了因这些处理抹杀数据之间的本质差异的可能性,比如,始点零像化会抹杀对应坐标相差一个常数的差异,初值单位化会抹杀相差常数倍的差异,等等不一一列举,这将导致差异较大的方案关联却较大的可能性无法排除。顺便指出:反映接近性的相关程度的关联度不宜作数据初始化变换,反映相似性相关程度的关联度必须将“作数据初始化变换不改变关联度值”做为合理性要求。
(2)直接计算各方案与理想方案之间的接近性关联度,没有涉及投影的计算,尽管绝大部分情形方案投影越接近理想方案就是方案接近理想方案,但无法排除例外情形的存在,至少是缺乏严格的理论保证,本方法避免了可能导致例外情形的发生的担忧。



