基于多面板天线的LOS信道容量分析*

1 引言

众所周知，多输入多输出（Multiple Input Multiple Out, MIMO）系统通过采用多天线可以有效提高频谱效率，其中多个独立的数据流可通过空间复用并行发送和接收，而无需额外的带宽[1]。但传统MIMO的频谱效率不再满足5G系统的需求，故大规模MIMO技术作为5G的关键技术之一，其天线阵元多达几十或几百。传统的MIMO技术研究大多假设通信环境中存在大量的散射体来实现空间复用[2]，但是当有效散射体减少时，视距（Line Of Sight,LOS）路径成为传输信息的主要途径，特别是在5G高频场景中，毫米波较高的传播损耗和较低的衍射能力，使得LOS传输成为主导，因此研究LOS信道的传输质量尤为重要。

在大规模MIMO系统中，天线阵元数目的显著增加会增大天线尺寸，使得瑞距离[3]变大（为天线阵列尺寸，为载波波长），此时发送端和接收端之间的距离可能小于瑞利距离，从而出现近场效应，导致天线阵列的相位、角度和延迟都会发生变化，平面波假设不再成立。文献[4]和[5]对大规模MIMO信道的测量结果表明对传统MIMO信道的远场假设可能不再适用。文献[6]中给出在4x4 MIMO均匀线性阵列（Uniform Linear Arrays，ULA）系统中，当频率为5.8Ghz、信噪比（Signal to Noise Ratio,SNR）为20dB时，近场中基于平面波模型（Plane Wave Model ,PWM）的容量为8.65bps/hz，而基于球面波模型（Spherical Wave Model ,SWM）能达到的最大容量为26.6bps/hz，传统的MIMO信道模型不适合直接应用于大规模MIMO信道建模。文献[7]和[8]研究了3D MIMO LOS信道容量，PWM和SWM的仿真结果表明信道容量取决于收发距离，波长和阵列大小。文献[9]研究了均匀矩形阵列（Uniform Rectangular Arrays，URA）中球面波和平面波建模差异，并对URA的天线阵元（天线间隔、传输距离和下倾角）进行优化设计以使得MIMO空间复用增益最大化。上述研究大多基于ULA或URA，将面临天线阵列尺寸较大的问题，如频率为6GHz、阵元间隔取半波长时，128阵元的ULA天线尺寸达到6.34米，很难进行实际部署。另一方面，在单面板内集成大量阵元会增加电路元件和天线阵元布线的复杂性，对电路冷却提出更高的要求。

尺寸相对紧凑的多面板天线能够有效避免上述问题。相较于ULA和URA，多面板天线能够节省硬件成本和功耗，特别是对于毫米波频段[10]。在天线面板间保持一定距离能够降低阵元间的相关性，提高MIMO系统高复用增益[11]。多面板阵列天线也有利于波束赋型技术的应用，文献[12]在大规模MIMO系统中提出了基于多面板天线的混合波束赋型技术，其性能甚至优于单面板天线。目前对多面板阵列天线暂无较多的研究，但随着大规模MIMO技术的实际应用，对多面板天线的研究将成为必然的趋势。

2 系统模型

假设在MIMO系统中，发送端阵列具有N个阵元，接收端阵列具有M个阵元，MIMO系统模型通常定义为：

根据上述系统模型，MIMO系统的信道容量可表示为：

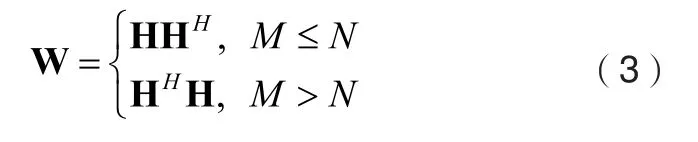
3 多面板天线几何模型

3.1 天线几何结构

目前常用的多面板阵列天线[10]如图1所示，由个面板组成，每个面板天线包含个天线阵元。其中，和分别表示面板的行数和列数，和分别表示面板的垂直间隔和水平间隔；同理，M和N分别表示单个面板内天线阵元的行数和列数，和分别表示单个面板内天线阵元的垂直间隔和水平间隔。

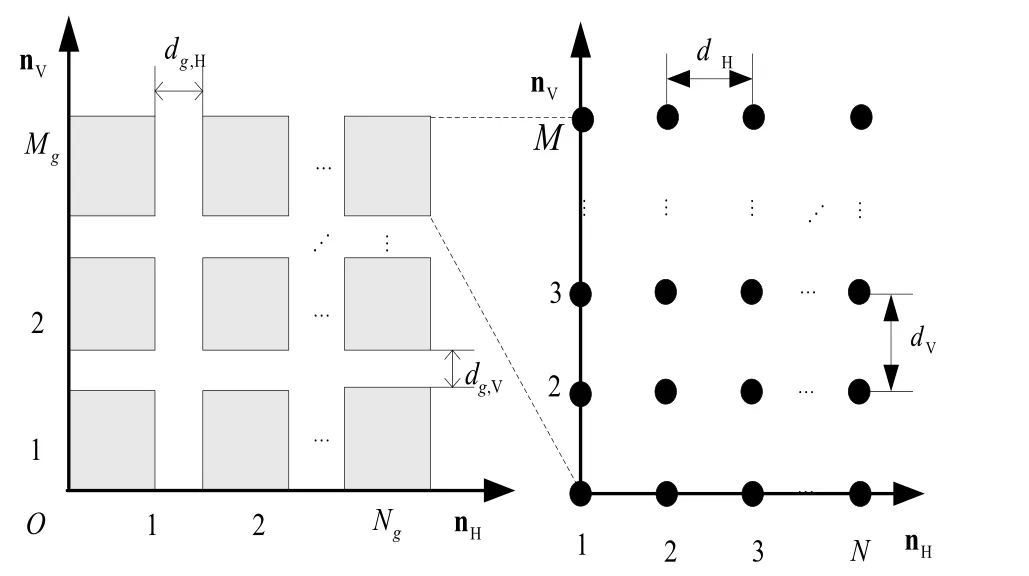
图1 多面板阵列天线

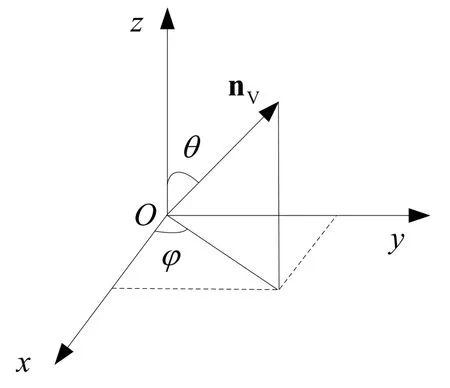
图2 面板天线垂直矢量

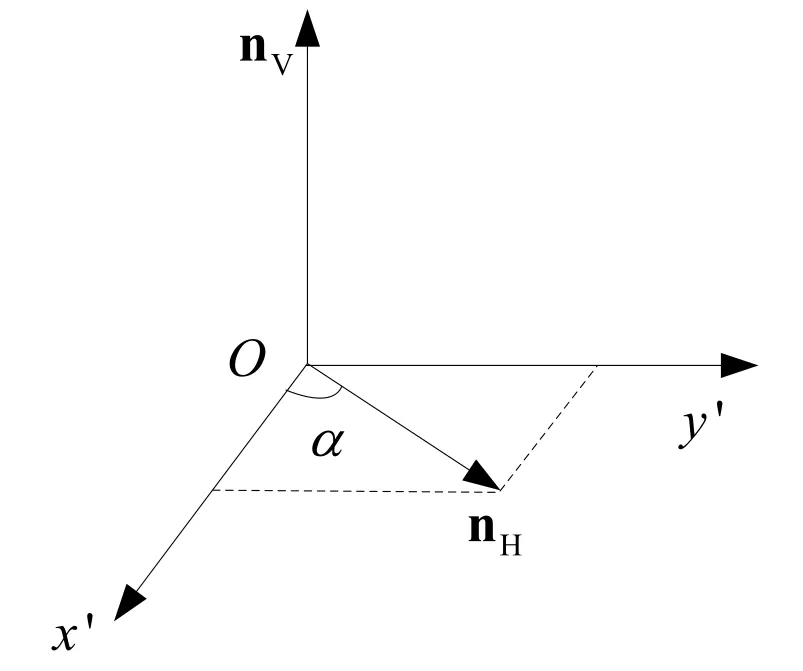
图3 面板天线水平矢量

在设计多面板阵列天线时需要考虑方向的随机性，文献[13]中仅考虑接收端阵列天线相对发送端天线在水平方向有一个角度偏转，不能体现阵列天线在实际应用中的位置关系。本文引入角度，使得收发端阵列天线均能够任意偏转。基于面板天线在笛卡尔坐标系中的几何关系，假设面板天线在垂直和水平方向的单位矢量分别为，如图1所示。根据图2可得水平方向单位矢量和笛卡尔坐标系的关系为：

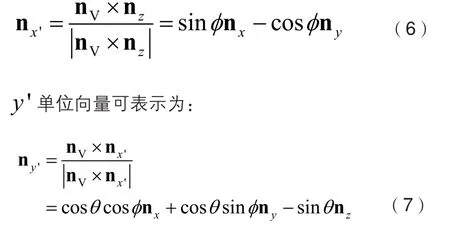
将式（6）和式（7）带入式（8）可得：

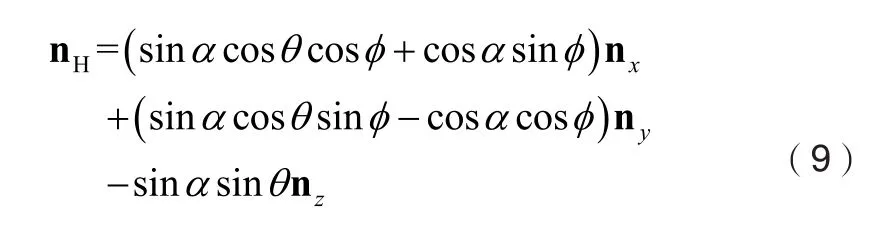
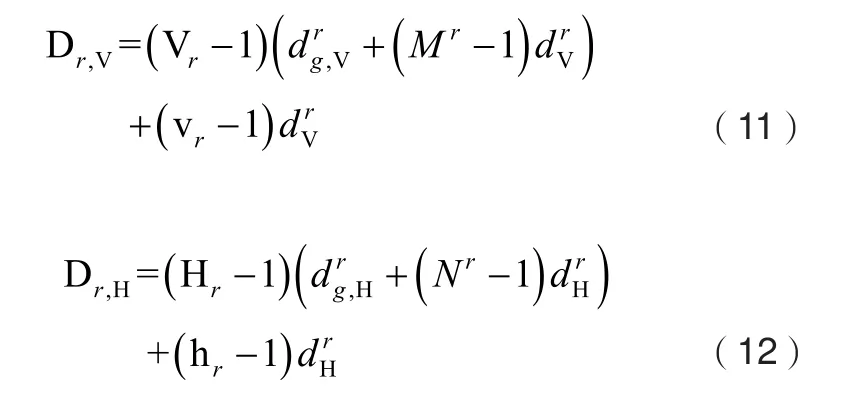
3.2 平面波模型

上一节描述了面板天线的矢量关系，本节主要基于阵元的位置进行平面波建模。如图4所示，在平面波建模过程中，根据上文定义的参考阵元，计算各阵元和参考阵元间的波程差，收发端的波程差均可通过角度、和进行表示。

图4 收发端多面板阵列天线

以接收端阵列为例，空间向量可表示为：

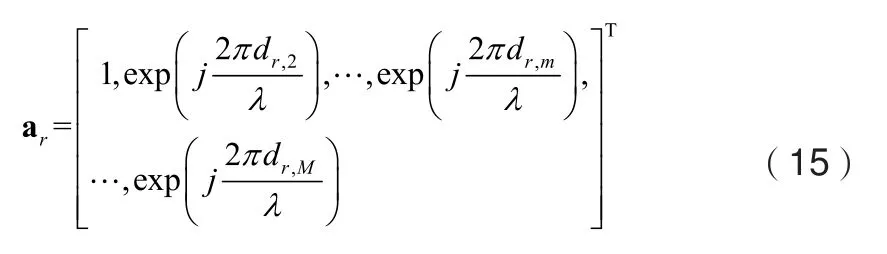
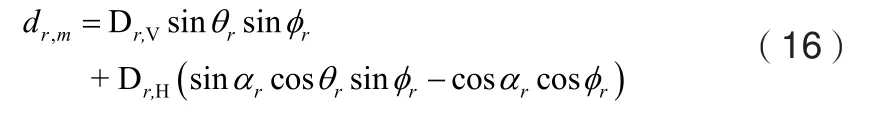
同理，发送端可表示为：

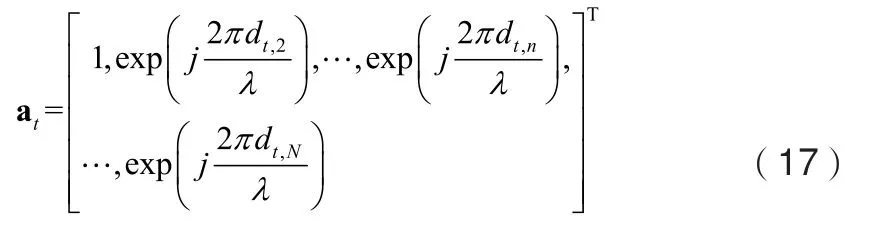
3.3 球面波模型

球形波模型在传播环境中使用精确的几何方法表征信道。传播环境如图4所示。尽管平面波模型在很多通信场景下都是准确的，但它在近距离通信中会大大低估MIMO增益。在这种情况下，应该考虑电磁波传播的真正球形特性，并且应该通过发送端和接收端天线阵元之间的路径距离来确定LOS信道矩阵。

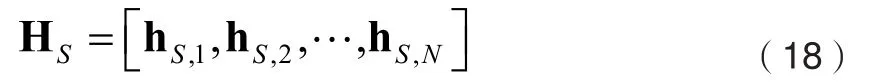
其中，下标表示球面波模型，N表示接收端阵元总数，信道矩阵的第n列可定义为：

4 仿真结果

为了分析多面板天线采用球面波模型和平面波模型对信道容量的影响因素，我们使用MATLAB软件分别计算出平面波模型和球面波模型下的LOS信道矩阵，然后分析对信道容量的影响因素。

图5描述了收发端距离对信道容量的影响，其中，接收端阵元总数（阵元布局均为（4，4，4，4）），发送端阵元总数，SNR=5dB，载波频率f=28GHz，阵列天线方向角：（收发阵列垂直于同一水平面且互相平行），阵元间隔，面板间隔（表示波长）。从图5可以观察到，平面波模型的信道容量恒定不变，这是由于平面波模型中LOS信道矩阵的秩始终为1，不受收发距离R的影响。然而，球面波模型中的信道容量受距离R的影响较大，随着距离R的增大，逐渐趋近于平面波模型的信道容量值。

此外，从图5可知面板天线的阵元布局也具有一定影响因素，其中，发送端天线阵元布局不变，接收端阵元布局分别为（2，2，2，2）、（2，4，1，2）和（4，4，1，1）、（1，16，1，1），则PWM的信道容量值恒定不变，但SWM的信道容量却各不相同，其主要原因是阵元布局改变了天线尺寸大小，从而间接影响信道容量值。例如，阵元布局为（2，2，2，2）时的天线尺寸最大，对应的信道容量值也最大。因此，在大规模MIMO的近距离通信中，SWM的信道容量值会受收发距离和天线阵元布局的影响，而PWM却不受此影响，但会低估实际的信道容量。

图5 PWM和SWM在不同距离和布局下的信道容量

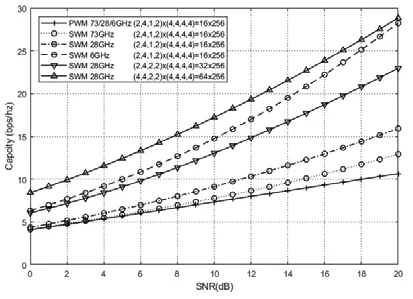
图6 PWM和SWM在不同SNR和频率下的信道容量

图6给出近距离LOS信道容量与SNR及天线阵元数的关系。其中，阵列天线方向角：，收发端阵列天线阵元间隔相同，收发端距离为R=5m。在M=256、N=16且收发端多面板天线阵元布局相同时，PWM的信道容量可由式（4）化简为，如图6所示，SNR=20dB时信道容量值为10.64（bps/Hz）。 同理，SWM的信道容量表达式由式（4）可化简为，SNR=20dB时的理论最大容量值为32.92（bps/Hz），由图可知，6GHz时的容量值为28.23（bps/Hz），此时各子信道不满足正交条件，故未能达到信道容量理论值。当频率为28GHz且信噪比一定时，对SWM的阵元数N取16、32和64时，MIMO系统的信道容量随收发天线阵元数以线性增长。图6未给出相应PWM的曲线，但PWM也满足该MIMO理论。同时，由图6可知，PWM的信道容量不随频率变化，即与波长大小无关。但观察SWM在6GHz、28GHz和73GHz的信道容量，发现SWM的信道容量随频率增大而减小。73GHz毫米波频段的SWM信道容量最小但仍高于PWM的信道容量，同时毫米波的波长较小，从另一个角度来看有利于大量阵元在面板内进行布局，因此多面板MIMO天线将成为毫米波大规模MIMO系统的首选。

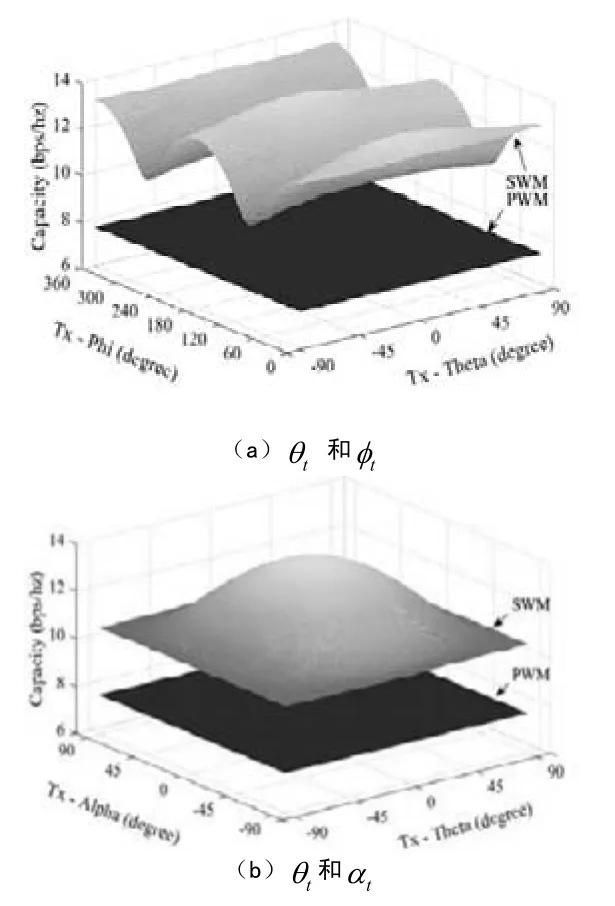
图7 PWM和SWM在不同阵列方向下的信道容量

接下来分析阵列天线方向对信道容量的影响。图7中仅改变发送端阵列天线的方向角，接收端阵列天线在平面内固定不变，即f=28GHz。在图 7（a）中，可以发现，平面波模型的信道容量不随角度而变，这是因为面板阵列天线进行旋转虽然会改变波程差，但LOS信道矩阵的秩依然为1。而SWM的信道容量随角度产生较大波动，当和时，信道容量值最大，因为该时刻发送端面板阵列天线最接近平行于接收端面板阵列天线。

5 结束语

在本文中，我们分析了基于三维多面板天线的大规模MIMO系统的LOS信道容量。其结果表明，在近距离LOS通信中，平面波模型不能有效反映信道容量的本质特征，会低估LOS的信道容量。球面波模型更能体现大规模MIMO的空间复用增益，比平面波模型更适用于大规模MIMO系统的近距离LOS传播场景。同时，波长、收发距离、阵元数目、阵元间隔和阵列方向等众多因素决定了球面波MIMO系统空间复用增益，未来可结合这些影响因素设计多面板天线，以实现空间复用增益的最大化，满足5G大规模MIMO天线的要求。