列表硬限制信号矢量检测算法研究*

1 引言

SM作为一种新颖的多天线传输技术，能够弥补MIMO系统信道间干扰、天线间同步以及硬件实现成本较高等缺陷。目前SM系统的许多研究都是基于理论层面的，信号检测算法的实现部分研究的比较少。应用于SM系统的分步检测算法能够提供较低的检测复杂度，但是其固有缺陷是检测性能较差。本文详细介绍了应用于SM系统的信号矢量检测(Signal Vector Based Detection, SVD)算法，在此基础上，通过引入新的处理方式给出了一种检测性能更好、检测复杂度更低的列表硬限制信号矢量检测(List-Hard limiting-Signal Vector Based Detection, L-HLSVD)算法。

2 信号矢量检测算法

SVD算法是一种典型的分步检测算法，即分两步检测激活天线索引和调制符号[1]。SVD算法通过牺牲检测性能来降低检测复杂度。接下来详细介绍SVD算法的检测原理，并分析其检测性能和检测复杂度。

2.1 算法原理

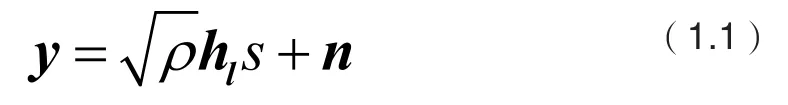
由公式（1.1）可知，在不考虑噪声影响的情况下，接收矢量是信道矢量和调制符号s的标量乘积，即。由于调制符号对目标向量的方向影响不大，因此与的方向一致，可以通过查找和接收矢量方向一致的信道矢量来确定发送端激活天线的索引。当然，由于系统存在噪声干扰，与的方向不可能完全一致，因此可能的接收矢量会存在于一定范围内。如图1所示，阴影部分内有三个方向不完全一致的矢量，虚线表示SM系统接收端的接收矢量，实线为方向在阴影范围内的信号矩阵的列向量。

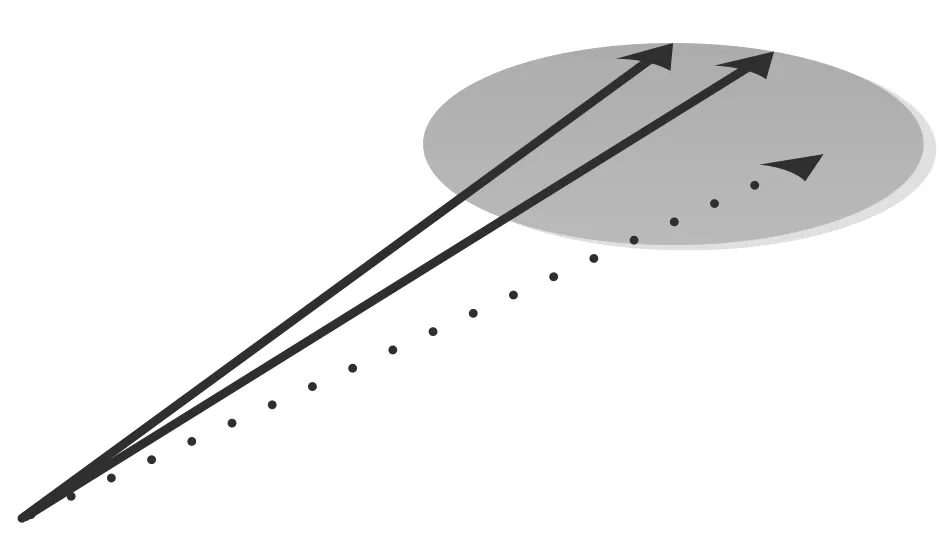
图1 受噪声影响的接收矢量分步图

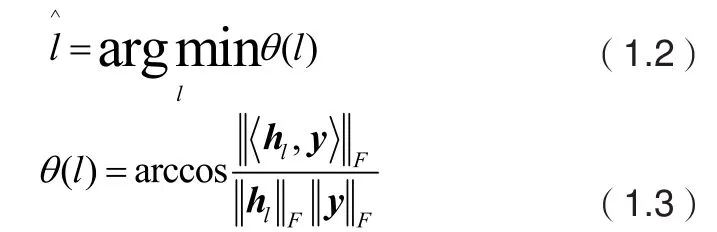
2.2 检测性能分析

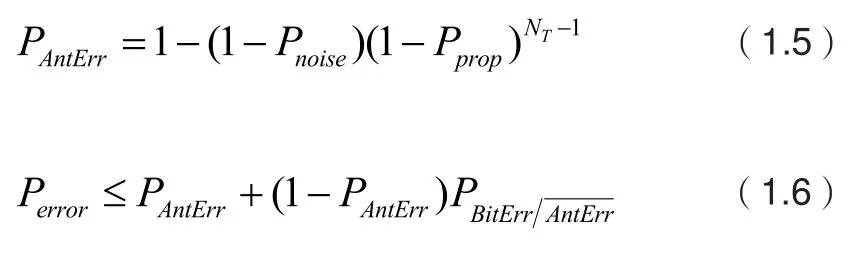
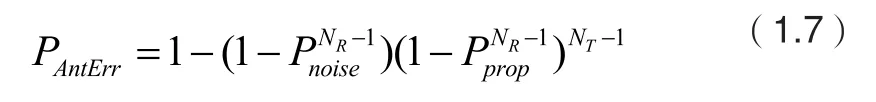
2.3 检测复杂度

为了说明和比较本文所研究的检测算法的检测复杂度，本文采用执行算法所需实数乘法运算的次数作为衡量检测复杂度的标准[2]。本节将首先给出实数乘法次数的具体统计方法，然后统计SVD算法的检测复杂度。

（1）实数统计方法：

为了说明实数统计方法，以应用于SM系统的ML检测算法为例。ML检测算法可以用公式公式（1.8）表示

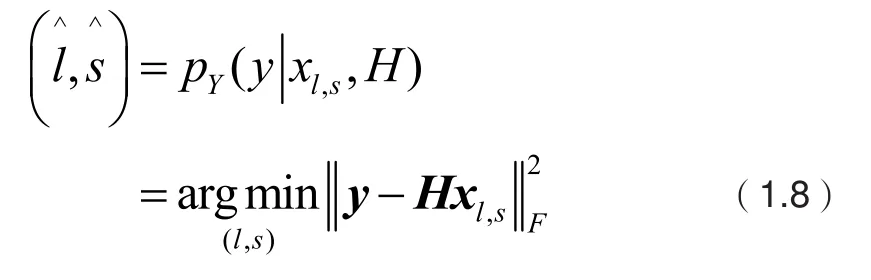
将公式（1.8）进行矩阵展开，可得：

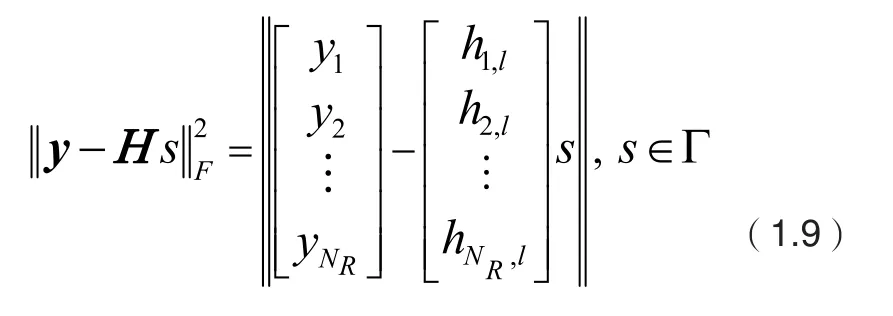
将公式（1.9）变形可得：

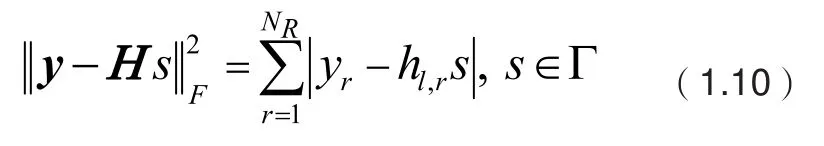
两个复数相乘会使用4次实数乘法运算；复数的求模运算是对其实部与虚部的平方和取开方的过程，只用做2次实数乘法运算。而都是复数形式，那么遍历一个可能的调制符号需要次实数乘法。发送端共有种激活天线索引，假设系统发送端采用阶星座调制，则ML检测算法的检测复杂度为。

（2）SVD算法的检测复杂度分析：

3 列表硬限制信号矢量检测算法

SVD算法与ML检测算法相比，检测复杂度明显更低[1]。但是由于一旦天线检测出错，容易连带调制符号被检测错误。SVD算法中，第一步就将激活天线索引确定了；然而，如果在第一步中不直接给出激活天线索引，而是给出激活天线索引的范围时，其错误概率可能会下降，从而增大算法的检测性能。此外，SVD检测算法的检测复杂度仍然和星座调制阶数成线性关系。SVD算法采用穷举搜索的方式进行调制符号的检测，此时可以看做是固定激活天线索引的ML检测，当调制阶数非常大时，检测复杂度也非常大。如果引入硬限制检测算法，则可以对采用方形或者矩形QAM调制的接收符号进行量化，从而在接收端直接通过比较操作后检测出正确的发送符号。硬限制检测能够避免SVD算法中穷举检测调制符号的弊端。因此，本节给出了性能优于传统SVD算法且复杂度不随线性增长的L-HL-SVD算法。

3.1 算法原理

鉴于以上分析，为了实现同时提高性能和降低检测复杂度的目的，将激活天线索引列表过程以及硬限制方法和SVD算法相结合，给出一种列表硬限制信号矢量检测算法。L-HL-SVD算法的具体流程如图2所示，现结合图2具体说明该算法的检测步骤。首先，根据上节的公式（1.3）计算出接收矢量与信道矩阵各列向量的夹角；然后从中选择个最小的夹角对应的列向量留下；接着根据硬限制方法求出上一步留下的列向量对应的调制符号，此时候选集变成候选对集，即，用集合表示；最后根据公式（2.1）求上一步中的候选对集中的最优解。

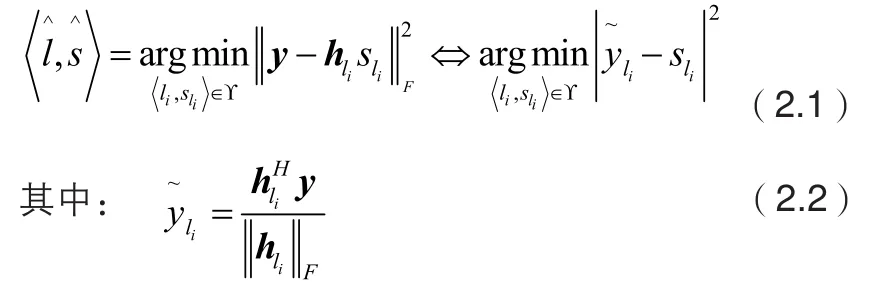
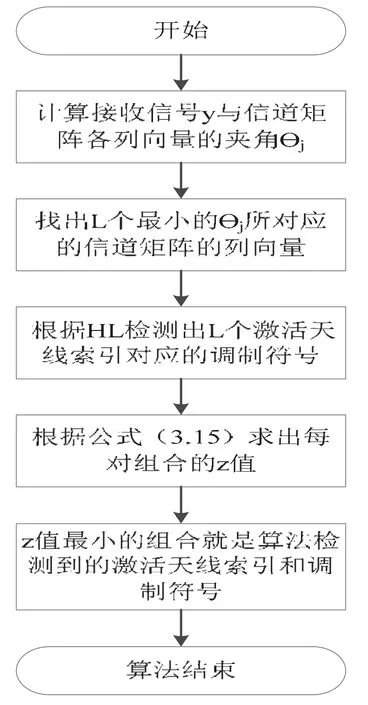
图2 L-HL-SVD算法流程图

下面具体说明硬限制方法。一个正方形或矩形QAM调制符号集可以被看作是两个PAM符号集的笛卡尔积[4]。此时具有个发射天线的SM系统检测复杂度将不再与星座调制阶数有关。换句话说，（1.4）中的符号检测的复杂度不再依赖于星座调制阶数。具体推导如下：

符号检测可以写成公式（2.3）的形式[5]。

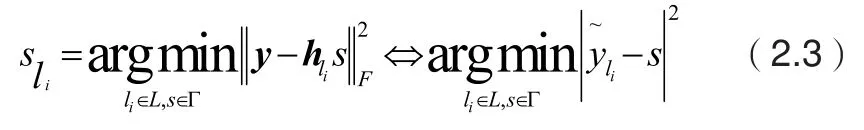
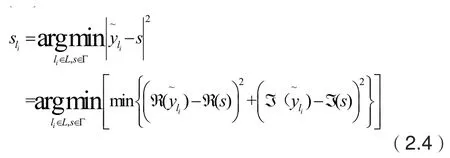
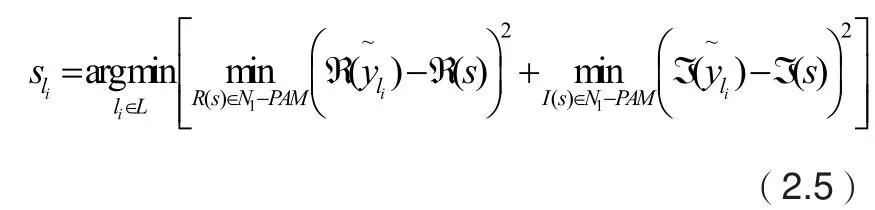
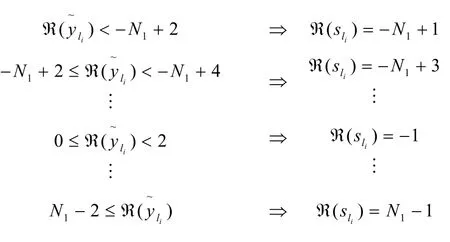
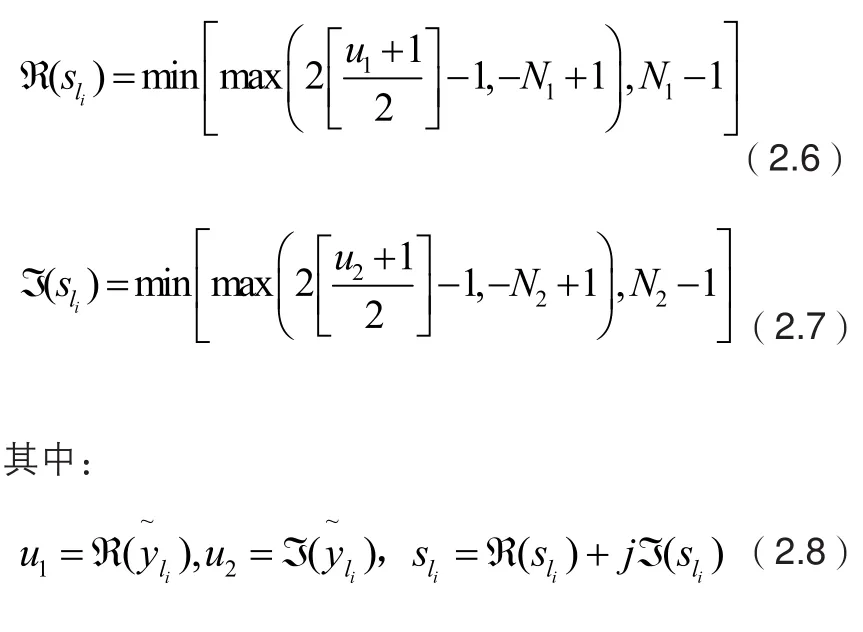
3.2 检测性能分析

L-HL-SVD算法与SVD算法相比，加入了激活天线索引候选集的概念，使SVD的第一步检测出的激活天线索引并非局限于一根，这样就降低了激活天线检测错误的概率，可以在一定程度上提升系统的性能。此外，硬限制判决并不会增加调制符号检测错误的概率[4]。因此L-HLSVD算法的检测性能相比于SVD算法会有一定的提升。

同SVD算法一样，造成激活天线索引检测错误的原因主要有两个：①由于的分布情况导致激活天线候选集中的天线对应的信道矢量正比于非候选集中的天线对应的信道矢量；②由于高斯噪声的影响，信道矢量的方向产生大幅度变化，使激活天线候选集中不包含正确的激活天线索引。由前面的分析可知，第一种情况下，当足够大，候选集中包含正确天线索引时，天线检测正确的概率为目标矢量与候选集以外天线对应的个信道矢量之间均不成正比，此时的概率为；当候选集中不包含正确的激活天线索引时，天线检测错误的概率仍然满足（1.5）式。第二种情况下，天线检测正确的概率大于等于，但是当等于时，检测错误的概率将非常低。为了便于分析，假设第二种情况下概率不变，两种情况下天线检测正确的概率满足公式（2.9），当时等号成立

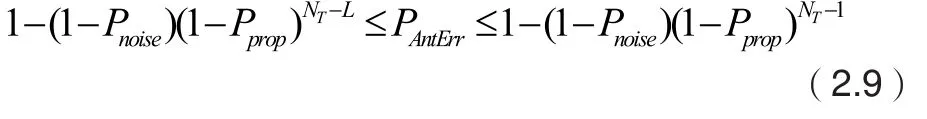
结合公式（2.9）与公式（1.5），与SVD算法相比，L-HL-SVD算法能够提高天线检测正确的概率，因此其检测性能优于SVD算法。

3.3 检测复杂度

4 仿真验证

为了验证L-HL-SVD算法的检测性能与检测复杂度，本小节将对本章研究的几种检测算法进行MATLAB仿真对比与分析。以系统的BER作为判断检测性能优劣的标准，以算法执行的乘法次数作为判断检测复杂度难易的标准。下面所有的仿真均在平坦瑞丽衰落信道下进行，并且接收端完全已知信道状态信息。

由于SVD算法和L-HL-SVD算法均属于分步检测算法，为了凸显两种算法的检测性能和检测复杂度，本节将对这两种算法和另一种分步检测算法——最大比合并(Maximum Ratio Combining, MRC)检测算法一起进行MATLAB仿真分析和比较。

4.1 性能分析

图3和图4分别是不同配置下本章所讨论的不同算法的性能对比图。图3是发送天线数是8，接收天线数是4、调制方式选用64QAM时不同算法的检测性能对比图。从图3可以知道，相比SVD算法，L-HL-SVD的检测性更好。当的L-HL-SVD算法相较SVD算法可以取得约0.4dB的性能增益。MRC算法、SVD算法以及本章研究的L-HL-SVD检测算法虽然都是分步检测算法，但是检测性能存在明显的差异。这三种算法中，MRC的检测性能最低。这是因为，MRC检测算法只适用于特定的信道环境[6]，而SVD和L-HL-SVD算法的适用性更广泛。此外，时的L-HL-SVD的检测性能要优于时的性能。这是因为，越大，激活天线候选集就越大，由激活天线索引检测出错导致的BER就越小。当时，第一步检测中只留下一根发送天线索引，相当于HL-SVD，此时复杂度最低，检测性能与SVD算法相差不大；当时，相当于第一步中没有舍弃不合适的发送天线索引，此时性能最好，但检测复杂度也最高。

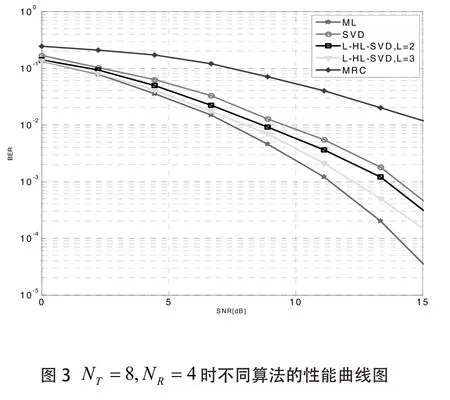
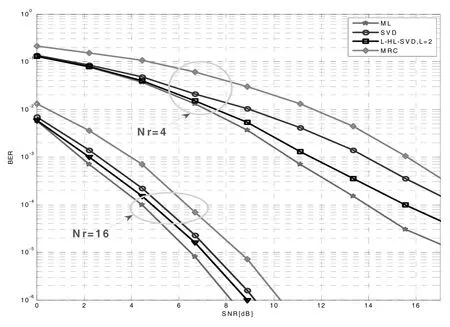
图4 不同接收天线数时不同算法的性能比较（Nt=8,M=16）

4.2 复杂度比较

表1 不同算法的复杂度

5 结论

本文主要研究了应用于SM系统的SVD算法，并在该算法的基础上给出了L-HL-SVD检测算法。L-HL-SVD算法在SVD算法的基础上增加了激活天线索引集的概念，大大提高了检测性能，且检测性能与的大小有关；此外，由于引入硬限制判决，L-HL-SVD算法的检测复杂度与星座调制阶数相互独立。仿真表明，L-HL-SVD算法相比SVD算法不仅能够改善检测性能，还能够降低检测复杂度。