联合能量收集中继与全双工目的节点的安全资源分配方案

王伟，李鑫睿，殷柳国，章国安，张士兵

（1. 南通大学电子信息学院，江苏 南通 226019；2. 南通先进通信技术研究院，江苏 南通 226019；3. 清华大学信息科学技术学院，北京 100084）

1 引言

随着5G网络即将商用，无线通信系统的能耗势必剧增。无线信能同传（SWIPT，simultaneous wireless information and power transfer）技术可有效解决无线通信中信息与能量同时传输这一难题，是未来无线通信的关键技术[1-5]。然而，由于 SWIPT系统本身具有的开放特性和广播特性，导致其信息极易被窃听者通过无线信道非法窃听。因此，SWIPT的物理层安全传输问题逐渐引起研究者的广泛关注[6-7]。

物理层安全技术可以有效地阻止窃听者通过非法接收获取信息[8-14]。由此，文献[8]研究了目的节点工作在全双工模式下的单输入单输出（SISO,single input single output）SWIPT系统，通过对时间切换系数和码字传输速率的联合优化来提升系统的保密吞吐量。在文献[8]模型的基础上，文献[9]研究了一种存在多个互不相干窃听者的全双工SWIPT系统，证明了功率分配因子、发送信噪比和保密信息速率对系统安全的重要性。文献[10]研究了基于全双工协作干扰源的 SWIPT系统，通过联合优化协作干扰源和目的节点的功率分配因子来提高系统的最大保密速率。文献[11]研究了基于全双工目的节点和能量收集窃听者的多输入单输出（MISO, multiple input sing output）通信系统，提出了一种联合优化信息波束成形、能量协方差以及人工噪声协方差的方法来提高系统保密性。文献[12]研究了一种基于人工噪声辅助多输入多输出（MIMO,multiple input multiple output）通信系统，通过对功率分配因子和波束成形参数联合优化来提高系统保密性。然而，文献[8-12]主要考虑的是单跳模型中物理层安全问题。在实际中，源节点有可能距离目的节点较远，无法直接进行通信。因此，研究基于SWIPT的中继系统更加具有现实意义[13-15]。文献[13]针对 SWIPT双跳中继系统，提出了分别在源节点和中继节点引入人工噪声的协同干扰方案，通过对上述2个节点的功率分配因子联合优化以提高系统的安全性能。在此基础上，文献[14]研究了多个中继协同干扰的 SWIPT系统安全传输问题。但文献[13-14]中的中继节点受能量和功率的限制，利用中继发送人工噪声必然会消耗中继收集的能量，同时引入的干扰信号也会影响有用信号的放大转发。因此，文献[15]研究一种全双工目的节点的双跳中继系统，该系统在接收信号的同时对窃听节点发送人工干扰，来提高系统保密性。然而，文献[13-15]都未考虑剩余自干扰的影响。

本文考虑了一种联合能量收集中继与全双工目的节点的SWIPT中继系统。其中，中继节点在功率分流模式下工作。本文的设计目标是在节点传输功率和中继收集能量等共同约束下，通过对功率分配因子和传输功率等参数的联合优化来实现系统保密速率最大化。由于此优化问题在数学上是非凸的，本文采用分步优化方法分别求得子问题的闭式解，然后利用迭代算法得到原问题的次优解。最后，通过数值仿真分析人工噪声强度、剩余自干扰大小、节点传输功率及中继放大倍数等因素对系统安全性能的影响。实验结果验证了本文所提方法的有效性。

2 系统描述及问题建模

2.1 系统模型

联合能量收集中继节点与全双工目的节点的安全传输模型如图1所示。源节点S距离目的节点D较远，需通过中继节点R把信息放大转发给目的节点D。而窃听节点E距离中继节点R较近，只能窃听到经过中继节点R的消息。其中，中继节点R实施功率分流处理，功率分配因子为ρ。假设该模型传输周期为T，在前时间段内，源节点向中继节点R发送信号，中继节点R对源节点S发送的信号实施信息解码和能量收集。在剩下的时间段内，中继节点R将采集到的信息放大转发给目的节点。由于目的节点D以全双工模式工作，在接收信号的同时，发送人工噪声干扰窃听节点E，来提高系统保密性。图1中，hsr、hrd、hde、hre、 fd分别为源节点S—中继节点R、中继节点R—目的节点D、目的节点D—窃听节点E、中继节点R—窃听节点E的信道向量、目的节点D的自干扰信道向量。

其中，xt表示源节点发送信号，其发射功率为为取数学期望；表示中继节点R引入噪声功率为2rσ的噪声信号。

图1 联合能量收集中继节点与全双工目的节点的安全传输模型

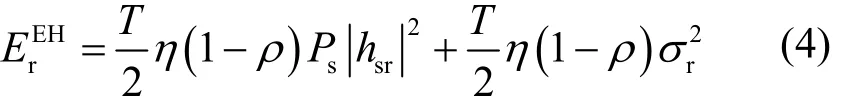
其中，β表示放大系数且β＞0。因此，中继节点R的传输功率为

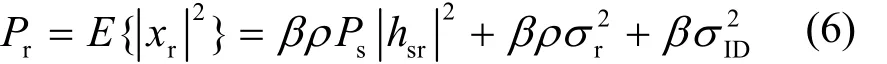
由于目的节点D为全双工模式，接收的信号中不仅包含中继节点R发送的信号，还包括自干扰信号和引入的噪声信号。经过自干扰消除后，目的节点D接收的信号为

其中，nSI为剩余自干扰信号，且满足为目的节点D引入的噪声。

由此得到目的节点D的接收信噪比和速率分别为

此外，窃听节点E接收的信号为

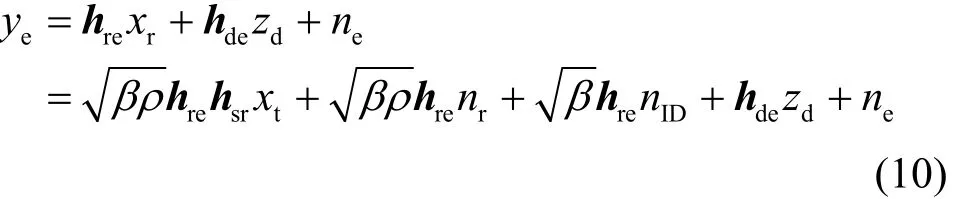
同理，窃听节点E的接收信干噪比和速率可得到

2.2 问题建模

本文目标是在节点传输功率和中继收集能量共同约束的条件下，通过对功率分配因子、传输功率等参数的联合优化来实现SWIPT中继系统保密速率最大化。因此，上述研究问题的数学模型可写为

其中，Pmax,s和Pmax,r分别表示源节点和目的节点的最大传输功率。根据式（4）、式（6）、式（9）和式（12），式（13）可以等效地表示为以下问题，如式（14）所示。

3 传输功率与功率分配因子的联合优化

优化问题式（14）中，目标函数和约束项存在优化变量的相互耦合情况，这导致式（14）很难直接求解。因此本文采用分步优化方案[4-5,18]来解决此非凸问题，即通过对两子问题的最优解进行分步迭代来获得原问题的次优解。

3.1 优化源点传输功率

在固定功率分配因子ρ情况下式（14）可等效为以下问题，如式（15）所示。

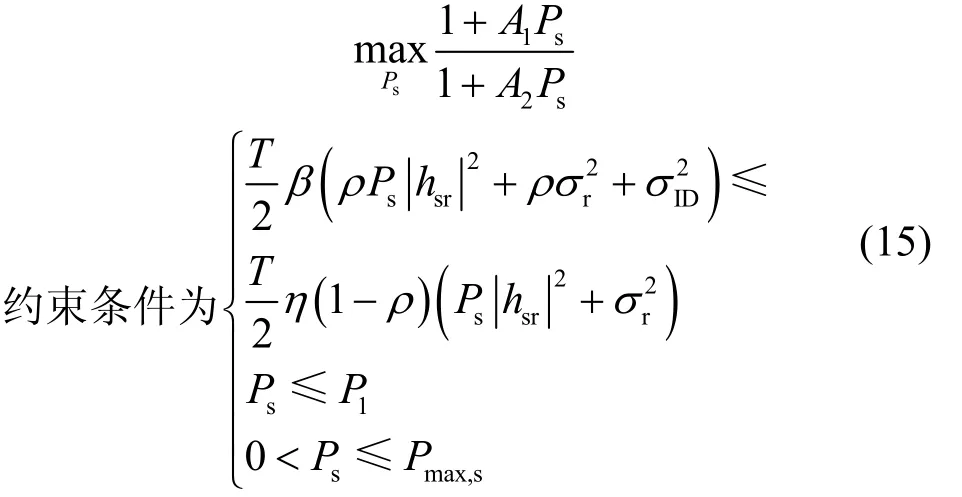
其中，

定理1当时，在能量受限约束下，式（15）可获得最优解如式（16）所示。

证明令式（15）目标函数为则有因为剩余自干扰信号是人工噪声信号经过自干扰消除后得到的（目前全双工的自干扰消除能力可以达到100 dB），故可得因此，在随机信道和噪声相当情况下，容易得到即则f关于P单调递增。此时，s若要使目标函数f取值最大，即在满足所有约束条件下，传输功率sP必定取其上界。由此，根据式（15）中sP的约束组合，得到最优解如式（16）所示。

证毕。

3.2 优化功率分配因子

通过固定sP来优化变量ρ，这里令此时式（14）可等效为以下问题，如式（17）所示。

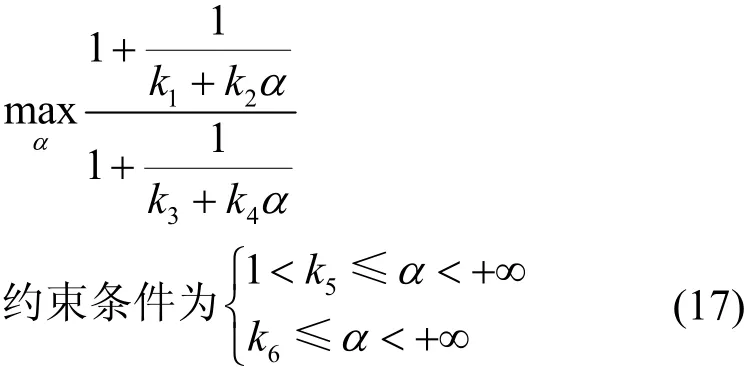
其中，

定理 2式（17）在满足的条件下，可获得最优解*ρ，如式（18）所示。

证明因为所以由此，式（17）通过恒等变形可重新表示为

证毕。

3.3 迭代优化算法

通过分别优化系统的传输功率sP和功率分配因子ρ后，使用迭代算法获得问题的次优解，算法步骤如下。

步骤1设迭代次数初值l=0，迭代次数最大值为次，收敛容限速率值速率差值

步骤2初始化

步骤3当和时执行步骤10；否则，执行步骤4。

步骤4根据得到的代入式（16），求出

步骤5根据得到的，代入式（18），求出

步骤6根据和计算

步骤7

步骤8

步骤9l=l+1；返回步骤3。

步骤10迭代结束，

3.4 算法收敛性分析

在任意th

l次迭代中，对于式（14），由于其 2个子问题可分别通过3.3小节的步骤4和步骤5来最优求解，因此，式（14）的目标函数一定为单调非减的。这是因为如果本次迭代导致目标值最大保密速率减少，可以保持或不变。此外，由于式（14）的约束条件是有界的，所以目标值最大保密速率也是有界的。根据单调性和有界性[4]，可以得出本文所提迭代算法一定是收敛的。

4 仿真验证

4.1 仿真参数设置

所有信道向量设置为独立同分布的瑞利衰落信道。除人工噪声外，所有节点的噪声功率设为相同，即如果没有特殊说明，所有仿真结果均为10 000次蒙特卡洛仿真的平均值。

4.2 仿真结果

首先给出所提联合优化算法与传统的梯度下降算法的性能比较，其中，中继节点的最大传输功率如图2所示。从图2 （a）中可以看出，随着源点最大发射功率Pmax,s的增加，2种算法系统的最大保密速率都是先增加后趋于饱和，这主要是因为受到Pmax,r的约束。与梯度下降算法相比，本文所提联合优化算法性能略好，但梯度下降算法因为受学习速率的影响，在极值点附近容易产生振荡。更为重要的是，与本文所提算法可得到子问题的闭合解相比，梯度下降法在不断更新模型参数的过程中需要更多的迭代次数，从而导致其具有更高的时间复杂度，2种算法的时间消耗对比如图2 （b）所示。从仿真结果可以看出，本文所提联合优化算法在性能略好的前提下可降低时间复杂度80%以上。

图2 不同算法性能比较

其次，图3就本文所提联合优化算法与固定功率分配因子算法的性能对比进行仿真，其中，中继节点最大传输功率。从图中可得出：当ρ较小时，随着源点最大传输功率Pmax,s的不断变大，最大保密速率也不断增加。当ρ较大时，由于受到Pmax,r的约束，随着Pmax,s的不断变大，最大保密速率先增加后趋于饱和。除此之外，当Pmax,s取较小值时，随着ρ的增加，信息传输所占比例变大，最大保密速率也随之增加。但随着取值不断增大，固定功率分配因子算法性能明显劣于本文联合优化算法性能，平均降低20%左右。这主要是因为在受到Pmax,r约束时，联合优化算法能充分利用ρ和sP的自由度来实现全局最优化处理。

图3 不同功率分配因子下的算法性能比较

图4给出了功率分配因子对系统保密性能的影响，其中，源节点最大传输功率从图中可得，在不同中继最大传输功率限制下，随着ρ的增加，系统最大保密速率呈先增加后减小的趋势。这是因为随着ρ的增加，系统的最大保密速率会增加。但当ρ增加到一定值时，会受到Pmax,r的约束，根据式（6），源点传输功率则会减小，导致系统最大保密速率随之降低。此外，根据仿真结果可得，系统最大保密速率随着中继最大传输功率的增大而增大，但其极值点依次向后移动。主要原因是随着Pmax,r增加，ρ也会相应地增大。另外，对应的最大保密速率极大值是对应极大值的2～3倍。

图5考虑不同剩余自干扰对系统最大保密速率的影响，其中，中继最大传输功率由仿真曲线图可知，随着剩余自干扰上升到200 mW，系统最大保密速率只有原来的左右。原因是式（8）分母项包含剩余自干扰，如果增加，系统最大保密速率就会随之减小。除此之外，由于受到Pmax,r的约束，系统的最大保密速率先增加后饱和。因此，自干扰消除对提高系统最大保密速率极为重要。

图6分析了不同人工噪声对系统最大保密速率的影响，其中，中继节点R最大传输功率根据仿真结果可知，随着人工噪声增加到2 000 mW，系统最大保密速率增加近4倍，但最终会趋向一个饱和值。这是因为式（11）的分母项包含人工噪声，随着的增加，窃听节点E接收速率逐渐减少，系统最大保密速率随之增加。然而，当过大时，因为目的节点D接收速率不变，窃听节点E接收速率趋于 0，所以系统最大保密速率趋向于饱和值。除此之外，从图中还可以发现，由于受到Pmax,r的约束，和的系统最大保密速率曲线近似重合。因此，在受到Pmax,r的约束条件下，一味地增加Pmax,s不一定能带来系统最大保密速率的增加。

图6 人工噪声对算法性能的影响

图8是不同源节点最大传输功率对系统安全传输性能影响的仿真曲线。从图8中可以看出，当Pmax,s较小时，随着Pmax,r的增加，最大保密速率基本保持不变。根据式（16）可知，如果Pmax,s较小，由于不会受到Pmax,r的约束，系统最大保密速率仅与Pmax,s有关。当Pmax,s较大时，由于受到约束，其系统最大保密速率随着Pmax,r的增大先增加后饱和。此外，从图中还可以看出，对应最大保密速率饱和值要比对应的饱和值高出2倍左右。因此，优化算法需要根据Pmax,r的大小仔细选择Pmax,s。

图7 人工噪声与剩余自干扰成比例变化对算法性能的影响

图8 源节点最大传输功率对算法性能的影响

图9是不同放大倍数对系统安全性能的影响曲线图，其中功率分配因子ρ=0.5，源节点最大传输功率从图中得出，在3种不同中继节点传输功率约束下，系统最大保密速率都呈先增加后减小趋势。这是因为随着β的不断增大，系统的最大保密速率不断增大，但当β增加到一定值时，会受到Pmax,r的约束，根据式（6），源点传输功率会随之减小，从而导致系统最大保密速率降低。此外，从仿真结果可以看出，随着中继节点最大传输功率增加，最大保密速率随之增大，但是其极值点依次向后移动。这是因为随着的增加，β值也会相应地增加。从仿真结果可以看出，对应的最大保密速率极大值是对应的极大值的2～3倍。

5 结束语

本文研究了联合能量收集中继节点与全双工目的节点的物理层安全传输问题，通过联合优化设计源节点传输功率和功率分配因子，达到系统保密速率最大化的目标。因为该非凸优化问题难以直接求解，所以本文采用分步优化方法分别求得两子问题的闭式解，然后利用收敛迭代算法得到原问题的次优解。数值仿真结果表明，与传统的梯度下降算法相比，本文所提算法在性能略好的前提下可降低时间复杂度80%以上。最后，研究了不同因素对系统安全通信性能的影响，能为人工噪声、功率分配因子及中继放大倍数等的有效选取提供了依据。