非线性四阶差分方程的振动性

高姗

(太原工业学院理学系，山西太原030008)

关于非线性四阶差分方程的研究现在已有许多重要结果。

考虑的非线性四阶差分方程为

其中k∈N0={n0,n0+1,…},n0是一个非负整数。Δ是差分算子。此方程的振动性在文献[1]中已经做过讨论，且给出了一个相关定理，对其结论进行了改进。

对于方程（1），规定：

1）α是一个正有理数；

2）{α(k)},{q(k)},{p(k)},{m(k)}是正序列；

3）{g(k)},{σ(k)},{n(k)}是非增实常数序列，对于任意的k∈n0,g(k)＜k,σ(k)＞k且lki→m∞g(k)=∞；

4）f,h,l:c(R,R)：满足

xf(x)＞0,f′(x)≥0,xh(x)＞0,h′(x)≥0(x≠0)。

方程（1）的解是指对于所有充分大的k≥n0∈N0满足(1)的序列{x(k)}。(1)的解{x(k)}是非振动的，若x是最终为正或最终为负的，否则称x是振动的。

定理1若对于方程（1），满足下列条件：

对于任意xy＞0都有：

若以下方程

的所有无界解

的所有有界解是振动的，则（1）是振动的。

证明令{x(k)}为（1）的最终正解，如文献[1]中定理1所证。需讨论以下三种情形a,b,c

情形a：假设Lix(k)＞0,i=1,2,3。k≥n0∈N0。则对于l≥m+1≥n0，有

上述不等式从m到k-1两边相加，有

令y(k)=L2(x)，用σ(k),(k+σ(k))/2代替k,m，有

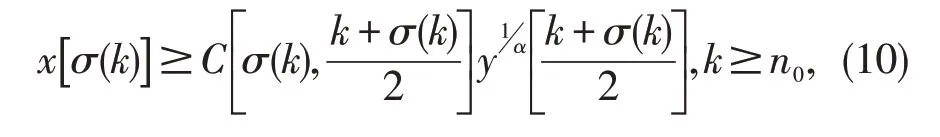
在（1）中应用（4）（9）。可知

则可知（7）有一个最终正解。

情形b：假设Lix(k)＞0，i=1,2。

L3x(k)＜0,k≥n0,则对于k≥m-1≥n0，有

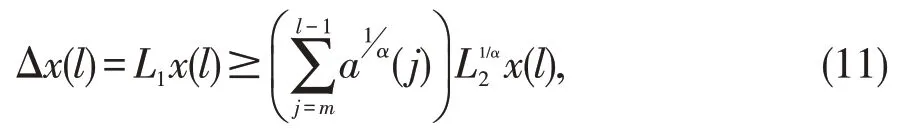
上述不等式两边从n0到k-1相加，有

令z(k)=L2x(k)，用g(k)代替k，有

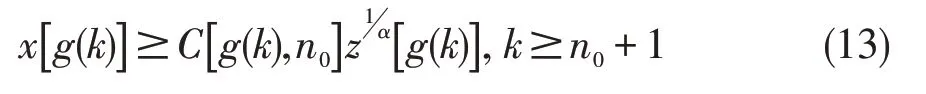
在(1)中应用(3),(13)，有

通过文献[2]中的一个结论，易知有一个最终正解。

情形c：假设L1x(k)＜0,L2x(k)＞0,L3x(k)＜0,k≥n0。如b可知（9）,不等式（11）两边从m到k-1≥m≥n0相加，有

令w(k)=L2x(k)。用(k+n(k))/2和n(k)代替k,m。由（2）知：

方程（1）中应用（3），（15），有

剩余的部分类似于b，因此省略，结论成立。

定理2条件（2）～（4）成立。若以下差分方程

的所有有界解是振动的，则（1）是振动的。

证明若{x(k)}是（1）的最终正解。须讨论三种情形a,b,c：

情形a：若L1x(k)＞0，i=1,2,3。k≥n0∈N0，则文献[1]中公式(15)成立。

用σ(k),(k+σ(k))/2,代替k,m。有

在方程（1）中应用准备知识中条件3，以及(19)。有

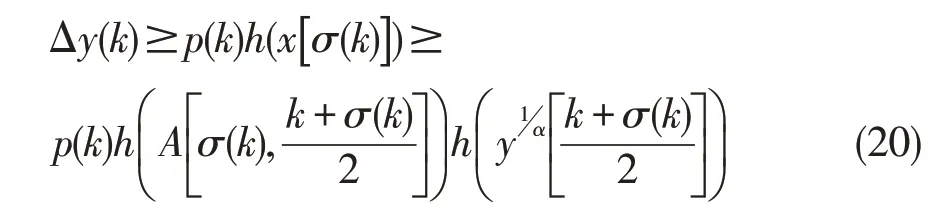
其中k≥n1≥n0。

易知(13)有一个最终正解。

情形b：若Lix(k)＞0，i=1,2。L3x(k)＜0,k≥n0∈N0。则由成立。

令j=k,-L3x(j)=z(j)。由（20）有

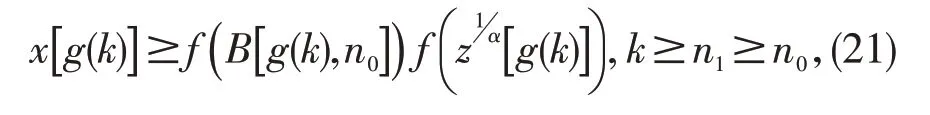
在(21)中应用（3）可知

或

Δz(k)则(16)有一个最终正解。

情形c：若L1x(k)＜0,L2x(k)＞0,L3x(k)＜0,k≥n0∈N0。令w(k)=-L3x(k),用(k+n(k))/2和n(k)代替k,m。知

在方程（1）中应用准备知识中条件2与上述不等式，有

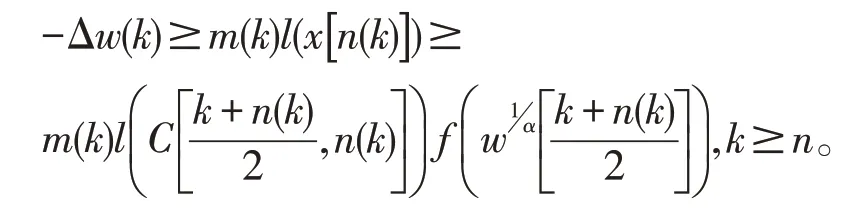
剩余步骤类似于,

结论得证。