基于相似度融合算法的主观题自动阅卷机制

李纪扣，韩建宇，王 嫄

(天津科技大学计算机科学与信息工程学院，天津 300457)

主观题目阅卷自动化是目前机考领域的前沿课题之一．主观题目答案中不同种语言、字符、语言模式差异所导致相似度计算中的复杂性和准确性问题是研究的重点方向[1]．文本结构差异、语义的不一致导致了相似度刻画的多样性，而且语义依存树下的相似度、基于知网的语义相似度等算法均对应用环境有较严格的要求[2]．基于语义依存树的相似度计算方法要先将语句的主干语义信息抽取成为语义表达式，再通过计算该语义表达式的相似度用以代替语句的相似度[3–4]；基于知网的相似度计算通过维护一个大规模语料库来得到文本的相似度[5]．通过挖掘独立词对(word to word)之间潜在语义关系的方法的必要条件是能够在语料库中找到词对的最优搭配[6–7]．这些方法均从语言学角度去分析语法特征，从语法上解决相似度问题．而对于理工科教学中题目答案的正确性判定，答案文本的关键词特征比其语法特征具有更高的重要度，并且基于关键词特征的相似度计算不需要大量的语法分析，能够降低相似度计算的复杂度[8]．在这种以文本结构作为切入点的模式下，有人提出了一种基于人工指定参数的相似度计算方法，该方法将关键词特征通过人为指定参数的方式组合得到文本的综合相似度[9]．以上的分析研究表明，对文本结构特征进行计算能够得到文本相似度，但计算过程中很少考虑语序特征．

针对特定背景下的主观题目自动阅卷，本文提出了一种基于相似度融合算法的相似度模型，在关键词匹配的基础上根据相对距离计算语序相似度，进而用统计回归分析方法对关键词相似度与词序相似度特征进行融合，得到文本的综合相似度，从而实现基于文本结构特征的主观题自动阅卷．

1 主观题目阅卷原理

主观题目阅卷采用基于文本结构的相似度模型实现，模型结构见图 1．模型主要包含关键词相似度计算方法、词序相似度计算方法以及相似度融合方法．由于文本中关键词同时代表着语义与结构特性，所以文本的相似度通过文本关键词特征来进行计算[10]．关键词特征相似度通过关键词相似度与词序相似度两维度分别进行计算，最后通过基于样本数据的二元回归分析实现不同维度的相似度融合，得到文本的综合相似度．

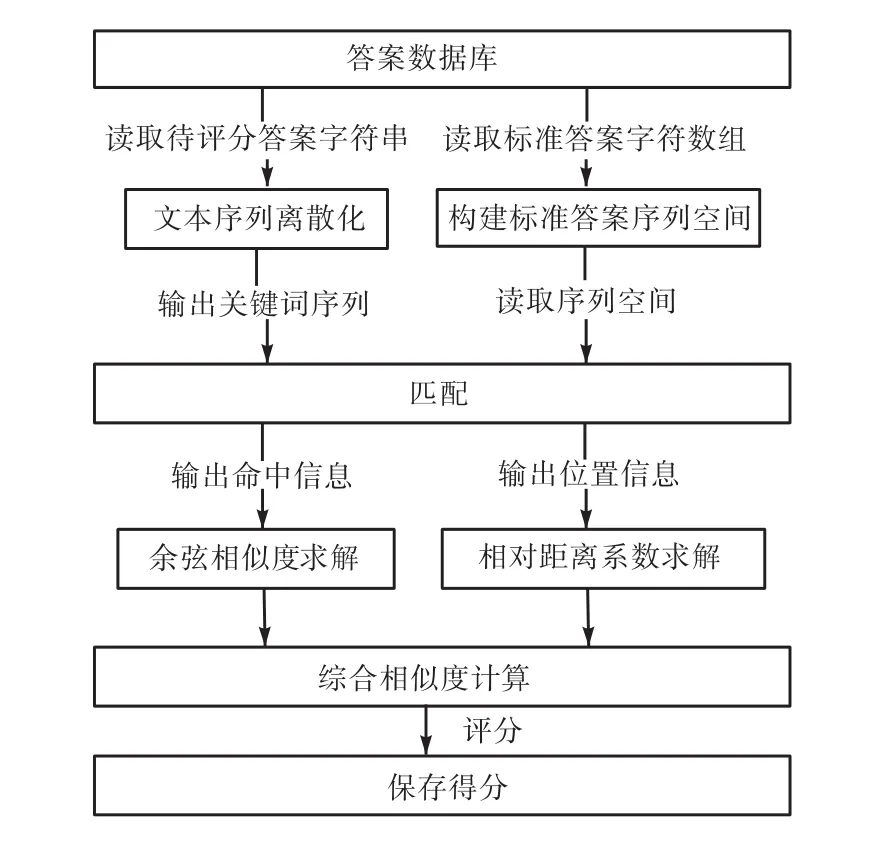
图1 基于文本结构的相似度模型结构Fig. 1 Similarity model structure based on text structure

在关键词特征相似度计算过程中，通过将答案关键词在标准答案关键词序列空间中进行搜索匹配，得到关键词的命中信息用于计算关键词相似度，得到位置信息用于计算词序相似度．其中，关键词相似度通过求解关键词序列的余弦向量夹角值得到[11]，词序相似度通过计算关键词在不同文本中的位置差的相对距离来得到．关键词不同维度的相似度可以抽象为影响文本综合相似度的因子，通过线性回归分析得到不同因子对于因变量的权重关系，即得到不同维度的相似度对于文本综合相似度的影响程度．将关键词特征相似度与文本综合相似度的二元线性回归函数作为题目答案评分准则函数进行题目评分．

2 方法设计与实现

2.1 关键词搜索匹配

在关键词搜索匹配前，通过数组 Trie树构建标准答案序列空间．数组 Trie树是将树形节点状态通过数组保存的一种字符前缀树，Trie树节点定义[12]为

typedef struct{

Py_ssize_hash；

PyObject * key；

PyObject * value

} PyDictEntry；

其中：key用于存储节点字符；value用于存储该节点的子节点以及当前节点的状态、子节点相对于当前节点的偏移值(数组 base)、当前节点的父节点状态(数组check)以及当前节点的位置标记值(index)．

基于 Trie树的序列空间构建过程包括初始状态确定、字符编码读取、状态转移、结果存储．在状态转移过程中，对于每一个关键词，从状态 s到 t满足base[s]＋code＝t、check[t]＝base[s]．字符编码用 code表示，状态转移中选取字符的 GBK2312编码集的十进制数取哈希映射后的值作为该值．序列空间构建过程如下：

(1)初始化 root节点为根节点，并设置 base[root]＝1作为起始状态．

(2)初始化base和check两个状态转移记录数组.

(3)找出root节点的子节点集合 root.childs，并修改 base数组和check数组，使得 check[root.childs]＝base[root]＝1成立．

(4)对于每一个子节点，找到一个初始值 begin，使得每一个子节点经过状态转移后均有空间进行存储．此时，设置当前的base值为该begin值．

(5)根据得到的 begin值与字符 code，通过状态转移方程对节点进行插入，同时修改字符的check值.

(6)对于每一个子节点，循环调用步骤(3)、步骤(4)，如果状态i对应某一个关键词，且base[i]＝0，那么令 base[i]＝(-1)*i；如果 base[i]！＝0，那么令base[i]＝(-1)*base[i]．即使得关键词词尾(叶子节点)其base值为负值．通过状态转移插入得到的Trie树如图2所示．

(7)经过逐个插入得到关键词字符的 i、base、check以及index数组列表．

在进行关键词搜索匹配时，首先对待评分答案进行分词、去停用词等操作，得到待评分答案的关键词集合．然后读取根据标准答案文本构建好的序列空间，根据当前状态与转移规则，通过字符编码进行状态转移，根据命中条件进行命中判定．

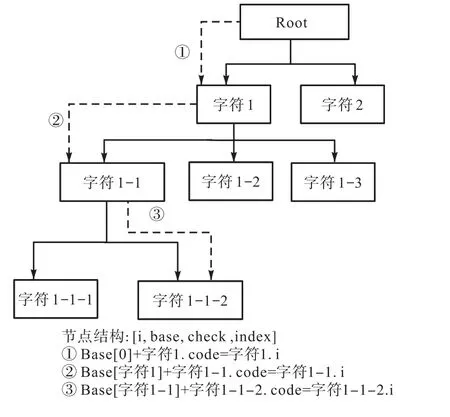
图2 Trie树示意图Fig. 2 Diagram of Trie tree

命中条件：定义当前状态为 p，如果 base[p]＝＝check[base[p]] && base[base[p]]＜0则查找命中．关键词搜索匹配流程见图3．

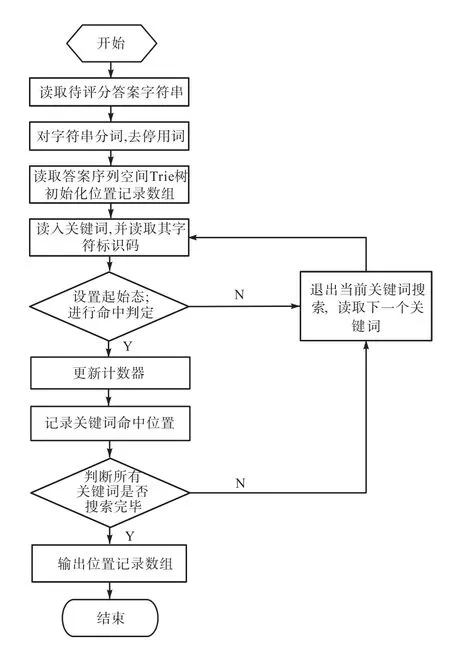
图3 关键词搜索匹配流程Fig. 3 Matching process of keywords

关键词搜索匹配的具体步骤如下：

(1)读取待匹配关键词，并将其拆解成为单个字符.

(2)读取构建好的关键词序列结果数组，并将root节点定义为起始状态p．

(3)读取第一个字符的编码 code，根据转移规则验证是否满足条件 base[p]＝＝check[base[p]] &&base[base[p]]＜0．如果满足，则当前字符的查找命中，继续读取下一个字符进行验证；如果不满足，修改位置记录数组值为0并退出查找过程．

(4)如果字符串中最后一个字符满足步骤(3)，则该字符串查找命中，修改对应位置记录数组的值为其index值并退出．

将待评分答案关键词集合中的每一个关键词都进行搜索匹配后，根据记录关键词位置情况的数组进行相似度特征计算．

2.2 相似度求解

相似度求解包括关键词相似度求解与词序相似度求解．在计算关键词相似度时，首先通过词袋模型对文本进行量化，将关键词结构特征转化为向量特征．在向量空间模型中，文本被拆解成单字或者词语组成的特征项集 D(T1，T2，…，Tn)，其中 Tk(1≤k≤n)是特征项，对应的是关键词．两个文本s1和s2之间的相似度可以用其特征项集对应的向量 V1，V2间夹角的余弦值表示．那么，标准答案文本与待评分答案文本的关键词相似度 C可以通过式(1)进行求解．

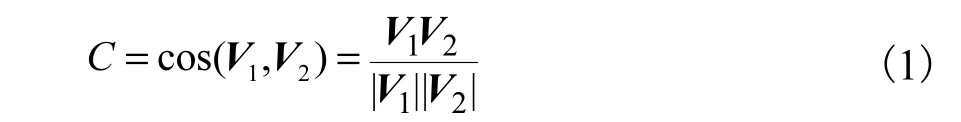
词序相似度通过相对距离进行计算．其中关键词的位置标记为关键词在文本特征项集中的序号；同一关键词在不同文本特征项集中的位置差值定义为相对距离，用于刻画其在语句内部的位置差异，相对距离越小，相似程度越大．关键词相对距离的计算方法见式(2)，其中dn2和dn1分别代表第n个关键词在两个不同文本s2、s1中的位置标记．

文本相对距离D的计算公式见式(3)．

将文本相对距离进行归一化，得到表示文本词序相似度的相对距离系数R，记为式(4)．

其中，Dmax为文本s1与文本s2间的最大相对距离．未命中关键词的相对距离 d记为(n-1)，当 s2中关键词全部缺失时，文本 s1与文本 s2间达到最大相对距离 Dmax＝(n-1)n．n为 s2中的元素个数，也就是集合长度．

2.3 相似度融合

在得到答案文本基于结构的相似度特征后，采用统计回归方法将不同维度的相似度以最优的权重融合成为文本的综合相似度．基于文本二维的结构相似度特征，将关键词相似度与词序相似度定义为自变量，学生答案得分与题目满分比值定义为因变量，定义二元线性回归方程

式中：b0为常数项；b1、b2为回归系数；C、R分别代表关键词相似度与词序相似度；y为答案得分与题目满分的比值；μi为随机误差．

多子句文本的相似度选取各子句相似度的平均值作为其相似度，计算公式见式(6)．Si为文本第i个子句的综合相似度．

3 实 验

首先需要采集特定学科背景下的主观题目人工阅卷结果作为样本数据，通过统计分析方法获得其相似度回归函数．本次实验采集“计算机体系结构”课程的500道已阅试题作为样本数据，数据来源为天津科技大学课程考试试题，试题类型包括简答题、名词解释题和论述题，每条数据包含题目、标准答案、学生答案与得分四项内容．

根据相似度算法求得学生答案与标准答案的关键词相似度 C、相对距离系数 R，并对得分与满分比值进行二元回归分析，得到回归函数见式(7)(随机误差忽略不计)．

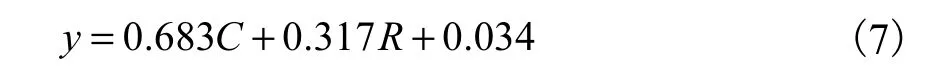
对回归函数进行显著性检验 F检验(显著性水平取 α＝0.05)得 F0.05＝2.735＜F(2497)＝3.014，接受线性回归显著假设．T检验得 T＝2.003，查表得2.003＞ T0.025/497＝1.965，接受函数回归参数显著有效假设．即该回归方程具有统计学意义，可以用来进行题目评分．

选取 200道“计算机体系结构”主观题目作为测试数据，其中包含 100道简答题、50道名词解释题、50道论述题．将题目满分标准化为 100分．对样本数据进行阅卷，首先调用中科大分词系统(NLPIR)进行分词与去停用词处理，将文本字符串处理成为关键词序列集合．然后通过数组 Trie树将关键词集合构建成为可供搜索的序列空间，在关键词搜索匹配的基础上计算关键词相似度与词序相似度作为文本不同维度的相似度，进而通过二元线性回归进行融合，得到答案文本的综合相似度．

实验对比方法采用人工指定参数的相似度计算方法[9]．该方法在关键词集合的基础上通过计算关键词相似度与集合贴近度，得到文本最终的相似度并将其作为题目得分权重．其中人工指定关键词权重参数 P＝0.7作为可信参数，语义贴近度阈值选取 0.15作为可信参数，ψ(A, B)表示关键词相似度，δ(A, B)表示文本 A、B贴近度，S0为题目满分．方法 2中的得分计算公式见式(8)．

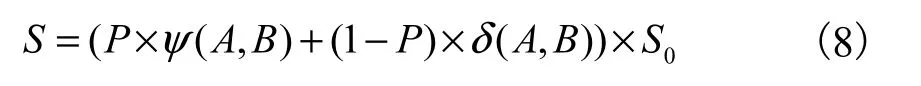
本文方法、对比方法及人工评阅的结果见图 4，分段统计结果见表1．

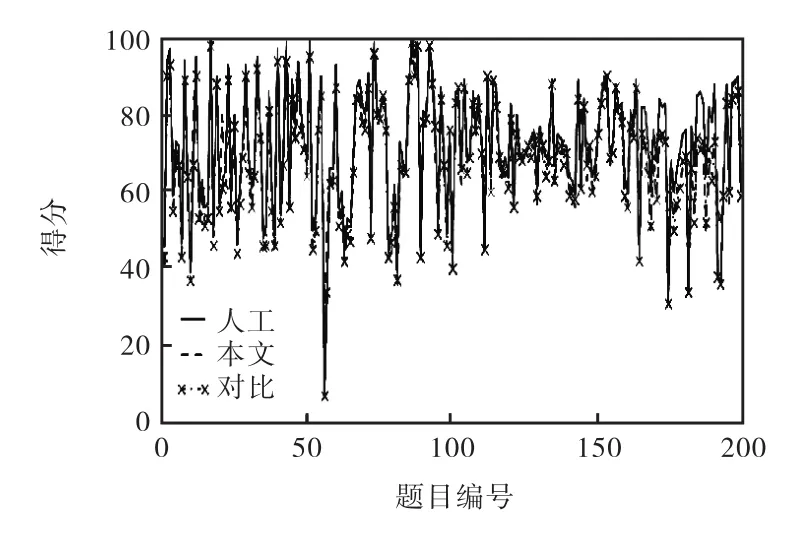
图4 阅卷结果对比Fig. 4 Comparison of grading results

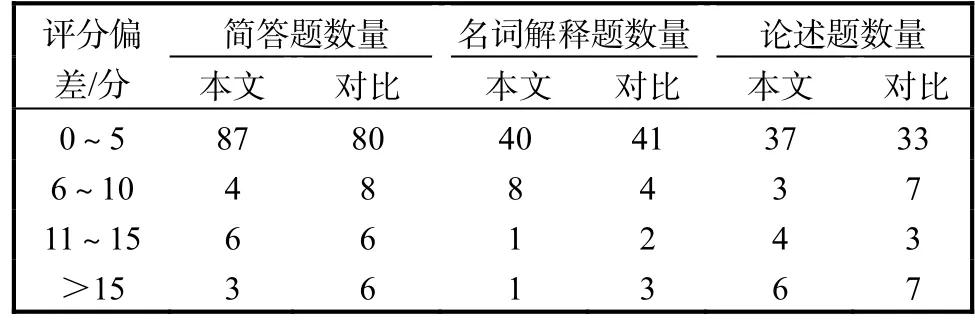
表1 分段统计结果Tab. 1 Results of section calculation

统计评分结果误差在 10分以内的题目数量，本文方法为 89.5%，对比方法为 86.5%．不同答案的用词差异导致关键词匹配命中率较低，致使相似度差异较大；论述题中包含较多子句，句子整体相似度求解时子句权重平均分配导致差异增加；简答题与名词解释题等短文本答案中的关键词特征明显，评阅效果较好；由于答案中的语序关系通过关键词的相对距离系数得到了更准确的描述，所以，对语序关系突出的题目评阅效果较好．评阅准确率整体较高，说明该模型方法对于主观试题有较好的评阅效果．

虽然在个别题目上存在评分偏差较大的情况，但是整体来看，本文方法的阅卷结果更加贴近人工阅卷结果，与人工评阅结果的两条评分曲线也更加吻合，阅卷结果基本一致．对于某些特定需求下的阅卷工作，该相似度模型可行有效．

4 结 语

对于学科背景下的主观题阅卷，本文通过 Trie树实现关键词匹配下的二维相似度模型，有效地避免了传统阅卷模式的句法树分析与向图分析的复杂性，节约了系统开销．其方法对于主观题目的快速阅卷具有一定的现实意义．