西藏农业区Ångström-Prescott公式参数选取研究

罗红英，李 丹，崔远来，田正野，罗玉峰



西藏农业区Ångström-Prescott公式参数选取研究

罗红英1,2，李 丹2，崔远来2，田正野1，罗玉峰1,2

（1. 西藏农牧学院水利土木工程学院，林芝 860000；2. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

针对西藏地区地域广阔、辐射站点少且分布不均匀等特征，为获得适用于西藏主要农业区的太阳总辐射计算模型参数，基于拉萨、狮泉河、那曲、昌都站1961—2004年的逐日太阳总辐射及日照时数数据，采用最小二乘法对Ångström-Prescott（AP）中的参数进行率定，利用2005—2016年的逐日观测数据对率定结果进行验证，并根据不同农业区划，由已知站点的参数值推求无辐射数据典型站点的经验参数，进而选取不同农业区划的经验参数。结果表明， FAO推荐的参数值并不完全适用于西藏地区，4个站点2个参数率定值的变化范围分别为0.18～0.26以及0.55～0.64。经验参数受纬度影响最大，其次是经度、海拔。拉萨站和昌都站计算值与实测值的吻合较好。5个不同农业区2个参数值变化范围分别为0.18～0.25及0.55～0.64。FAO推荐值在高原温带半湿润区以及高原温带半干旱区适用性较好。该研究成果可为无辐射实测地区的太阳辐射值和作物腾发量的计算提供依据。

辐射；高程；维度；Ångström-Prescott公式；西藏；参数估计

0 引 言

太阳辐射是决定一个地区光能生产能力的重要变量，也是影响陆地与大气水分与能量交换最重要的驱动要素；太阳总辐射（R）是地表蒸散发的主要能量来源[1-3]。合理确定R是分析地表能量平衡关系，评价参考作物腾发量（reference evapotranspiration，ET0）等相关水文气候变量的重要前提之一[4-6]。目前国际上计算ET0时所广泛采用的Penman—Monteith （PM）[7]方法，也需要相应的辐射数据。然而，与其他常规气象资料如温度、降雨的观测相比，由于太阳辐射实测仪器的维护、校正复杂，成本高，即使在国内覆盖面很大的气象观测网络中，具有实测太阳辐射的站点仍相对较少[8-9]。目前全国辐射站点只有124个，而建站时间在30 a以上的只有70个，西藏地区只有拉萨、狮泉河、那曲和昌都4个辐射观测点。针对西藏地域广阔、辐射站点少且分布不均匀等特性，为获得总辐射在西藏地区的分布特征资料，往往借助于间接的计算方法，以便用无辐射的站点上的气象要素 值来求算总辐射。国内外针对计算R的方法已有大量研究[10-15]，钟强等[16-18]在西藏高原区的辐射计算方面做出了很多贡献。然而此类研究多数是从大范围的研究对象考虑的，方法主要以太阳总辐射的气候学计算为主，模型参数详细选取的工作较少涉及。西藏地区太阳辐射观测台站少，不能满足分布规律研究和实际开发应用的需要。因此，探讨适用于西藏主要农业区R的估算方法，分析经典Ångström-Prescott（AP）模型系数的适用性，提出适用于主要农业区的模型参数以期得到太阳辐射的变化规律及精准的ET0，对农业长期用水规划具有重要的指导意义，有利于合理开发和利用西藏的水资源。

1 材料与方法

1.1 研究区概况

西藏自治区位于中国西南部，地理位置介于78°27¢～ 93°06¢E、26°50¢～36°53¢N之间，区域面积约占全国总面积的1/8。西藏占据青藏高原的主体部分，平均海拔4 000 m以上，地势由西北向东南倾斜，地形复杂多变。气候纬度地带性和垂直地带性明显，参照《西藏农业气候资源区划》[19]，根据西藏的气候、土壤、植被和地形条件特点将西藏分为5个区域：高原温带半湿润区、高原温带半干旱区、高原温凉半湿润区、高原温带干旱区以及高原寒带干旱区。西藏共包含38个气象站点，但只有其中的4个站点（拉萨、狮泉河、那曲以及昌都）有实测辐射资料，其他皆为无辐射实测资料的气象站点，站点分布及所属农业分区见图1及表1。就行政区域而言，林芝是西藏主要的粮食产区之一，位于高原温带半湿润区，耕地面积占西藏总耕地面积的8.0%。日喀则素有“西藏粮仓”之称，地处高原温带半干旱区，耕地面积占比为34.8%。索县是西藏典型的半农半牧区，属高原温凉半湿润区。故除将具有辐射实测资料的站点作为典型站外，分别选取这3个站点作为其所属农业分区的典型站。

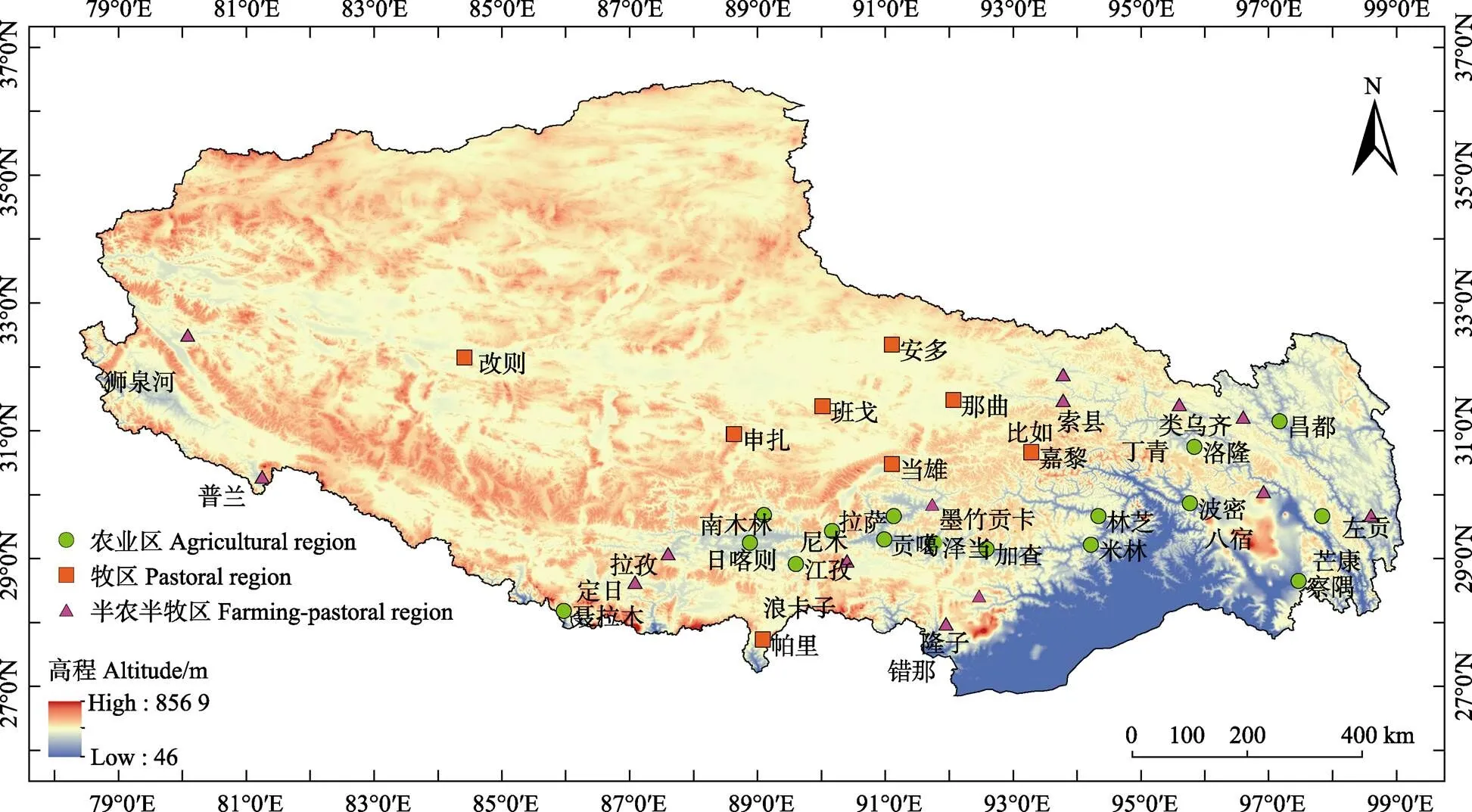
图1 西藏38个气象站点的分布

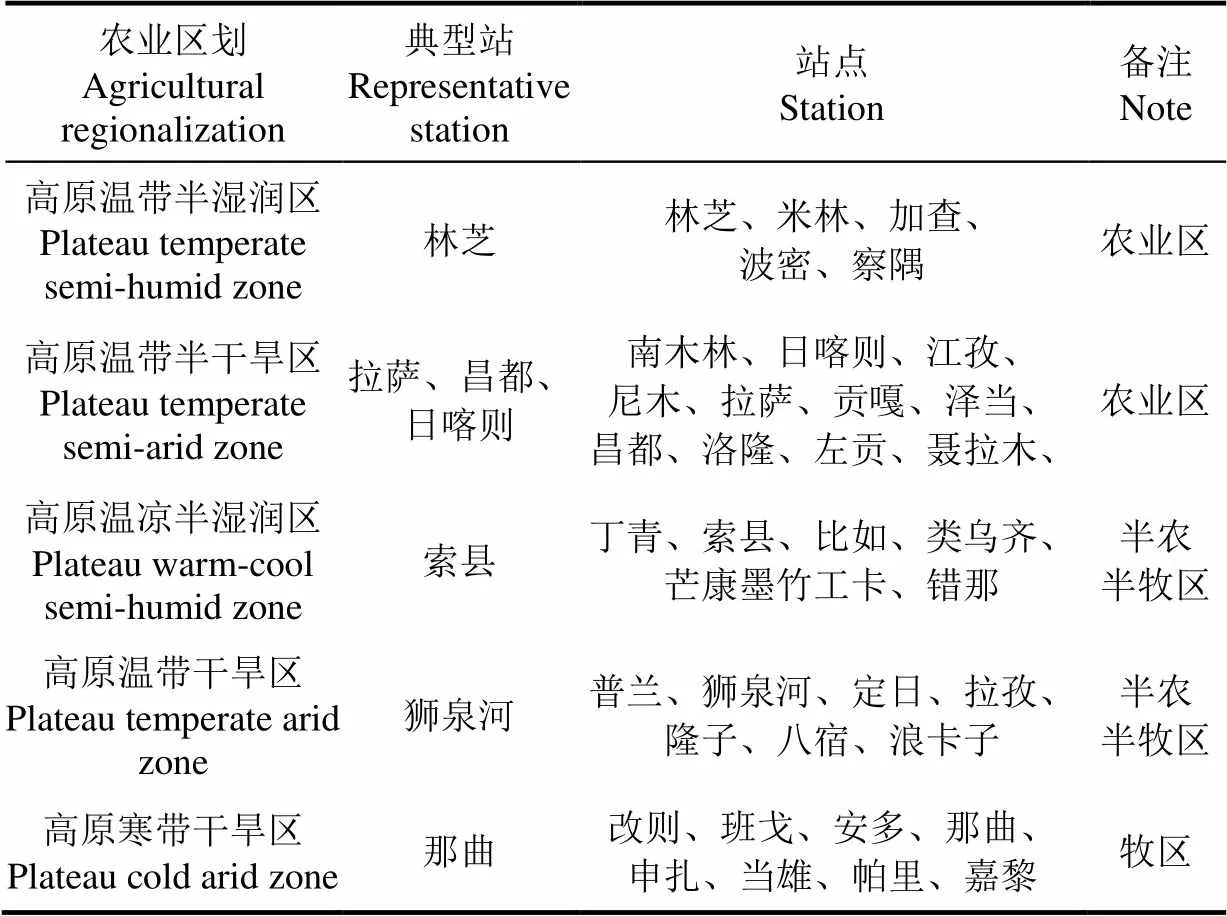
表1 西藏农业区划及典型站点

1.2 数据来源

收集了现有所有4个辐射站的逐日太阳总辐射R和日照时数的实测资料，站点的名称、地理位置及所在的分区如表2所示。对于不能如实反映实际状况的数据通过对比法进行了筛选和剔除，如R大于大气顶层辐射（R）时则剔除掉此数据；若在数据中发现有缺测现象，对于辐射数据中出现连续3 d内缺测的情况通过直线插值求得，对于>3 d的连续缺测记录，则进行剔除，即在计算平均值时不考虑这些天的辐射数据。

1.3 太阳辐射计算方法

1998年联合国粮农组织（Food and Agriculture Organization of the United Nations，FAO）特别推荐的标准PM方程中的辐射计算采用AP模型[7,20-21]，即：

式中R为太阳总辐射，MJ/(m2·d)；R为大气顶层辐射，MJ/(m2·d)；、为Ångström-Prescott系数，反映外空辐射受大气斜射率、空气中水汽含量、微尘粒多少等因素影响而造成的衰减特征，二者之和为晴空条件下辐射透射率；为实际日照时数，h；为理论日照时数或最大可能日照时数，h。月、年大气顶层辐射量R是由大气顶层辐射量公式计算每日R，然后采用逐日求和的精确累计法得到。

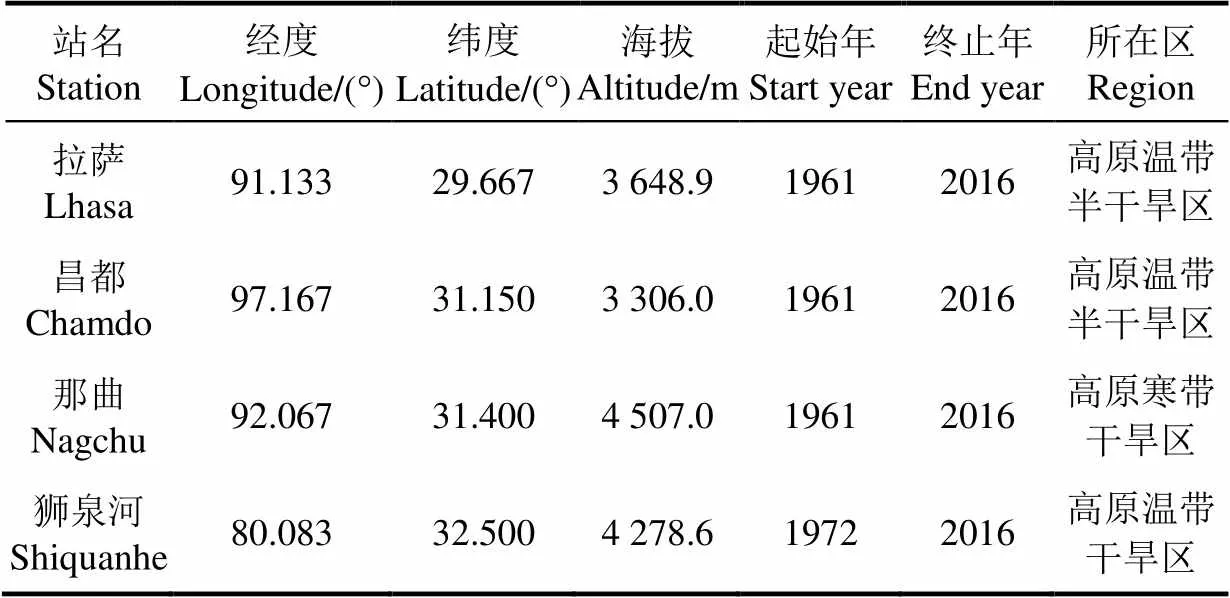
表2 辐射站基本信息

注：台站信息资料来自国家气象信息中心。

Note：Station information is from National Meteorological Information Center.

R的计算公式[4,7]为

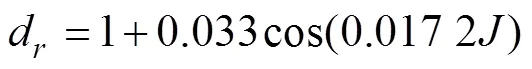
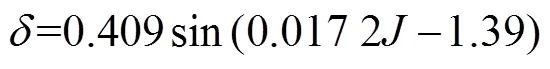
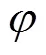
1.4 模型评价方法

采用标准差（standard deviation，SD）、平均绝对误差（mean absolute error，MAE）以及平均绝对百分误差（mean absolute percentage error，MAPE）这3个指标来评价率定后AP模型的准确性，计算公式如下：

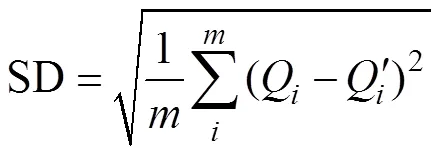
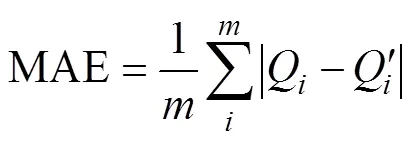
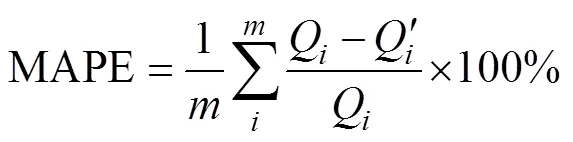
2 结果与分析

2.1 AP模型系数率定及验证结果

采用式（2）～（6）计算R和，基于西藏4个辐射站1961—2004年的实测R和实测，以R/R为因变量，以/为自变量，在Origin软件中运用最小二乘法拟合式（1），得到各站点的系数、；再采用2005—2016年的逐日观测数据对计算结果进行验证。

将率定后AP模型计算的R结果与实际观测数据对比分析。由4个站点太阳总辐射计算值与实测值的误差分析结果可以看出（图2和图3），率定期回归直线斜率皆在0.7以上，统计指标值皆在可接受的范围内。验证期拉萨、狮泉河、那曲以及昌都站的SD值在1.75～2.80 MJ/(m2·d)之间，拉萨、昌都站计算值的准确性高于狮泉河、那曲站计算值的准确性。其中拉萨站的SD值最小，为1.75 MJ/(m2·d)，而那曲站的SD值最大，计算值精度较差。该4个站点MAE值的变化范围为1.27～2.03 MJ/(m2·d)，拉萨站的MAE值最小，表明拉萨站的计算结果更为接近实测值。分析4个站点MAPE值的正负值可以发现，拉萨、昌都以及狮泉河站的MAPE值小于0，表明这3个站R计算值小于实测值，但拉萨和昌都的MAPE值较接近于0。那曲站的MAPE值大于0，表明该站R计算值总体偏大。总体来看，拉萨站和昌都站计算值与实测值的吻合较好。对2005—2016年模拟得到的逐日太阳辐射与实际观测值进行相关分析。可以看出，二者的相关性均达到了显著相关水平，4个站点太阳辐射的计算值与实测值的拟合度为0.843～0.888，回归直线的斜率为0.844～0.940之间，表明该模拟方法基本反映实际逐日太阳辐射值的变化，计算方程选取的参数较为准确。

图2 率定期太阳日辐射计算值与实测值比较

图3 验证期太阳日辐射计算值与实测值比较

将率定后的、值与FAO推荐值进行比较，以判断FAO推荐值在西藏地区的适用性，结果如表3所示。可见，参数、的变化范围分别为0.18～0.26和0.55～0.64，与FAO建议值[22]有一定差别。总体来看，系数的率定值与FAO推荐值的相对偏差在-28%至2%之间，系数的相对偏差范围为10%～28%。其中，拉萨站、的率定值与FAO的推荐值较为接近，系数、的相对偏差分别为2%及10%，其他3个站点的率定值与FAO推荐值相对偏差约在25%左右。除拉萨站系数的率定值略高于FAO的推荐值以外，其他3个站点系数的率定值皆明显低于推荐值。4个站点系数的率定值都明显高于FAO的推荐值。综上，FAO推荐的经验参数并不完全适用于地形地势复杂，地域广阔的西藏地区。AP模型系数、包含了各种物理因子（如水汽、气溶胶、云的光学性质等）对地面总辐射的综合影响。西藏高原地理环境复杂，水汽、气溶胶的含量空间差异较大[23-24]。由于在不同地区和不同月份的实测总辐射资料往往是不同的，所以拟合得到的经验系数、值结果往往有较大的空间差异。

表3 不同站点a和b率定值与推荐值的对比分析

注：FAO建议使用的为0.25，为0.55。

Note: Recommendedandvalues by FAO are 0.25 and 0.55, respectively.

2.2 AP模型系数影响因素分析

绘制、值与纬度之间的关系，见图4。、值皆与纬度之间具有一定的相关性，系数随站点纬度的增加而降低，且拟合度达0.8以上；系数随纬度的增加而有增加的趋势，拟合度为0.6。可以看出，系数受纬度的影响较系数受纬度的影响更为明显。图4所揭示的这种相关性，一定程度上反映了经验系数、在区域上的变化规律，对于参数在区域上的拓展具有一定的价值。此外，图4点绘了、值与经度、海拔的关系。由图可以看出，系数随经度的增加而有增加的趋势，系数随经度的增加而有下降的趋势，但系数、受经度的影响并不明显，拟合度只有0.06和0.17。类似地，由图4可知，AP系数、与海拔的关系并不明显，系数、随海拔的升高仅呈现微弱的下降趋势。由此可见，AP系数、受纬度影响最为显著，其次是经度，与海拔高度无明显相关性。

在站点少（只有狮泉河、那曲、拉萨和昌都4个辐射观测点），时间序列短的状况下研究计算太阳辐射，不同的学者得到的同区域、值存在差异，如表4所示，前人研究表明，青藏高原的AP模型系数、值范围分别在0.166～0.290和0.523～0.792之间，变异系数分别为20%和15%，差异较大。翁笃鸣[31]在20世纪60年代将全国划分为华南、华中、华北和西北4个不同区域，根据50个站点2～3 a的实测数据，提出了各区域、的建议取值。祝昌汉等[27-28]基于全国75个辐日射站1957—1977年的辐射观测数据，讨论了、的空间变化及影响因素，指出分区域配置、，可提高太阳总辐射的计算精度。中国地区参数的变化范围为0.10～0.35，的大致变化范围为0.35～0.7。根据左大康等[25]的研究，青藏高原区的变化范围为0.17～0.29，的变化范围为0.52～0.79。本文以西藏4个辐射站点资料通过最小二乘法回归，获得、率定值，参数、的变化范围分别为0.18～0.26和0.55～0.64，与前人研究结果的变化规律较为一致，采用的辐射资料为近50 a长系列的实测资料，率定结果更具有代表性。

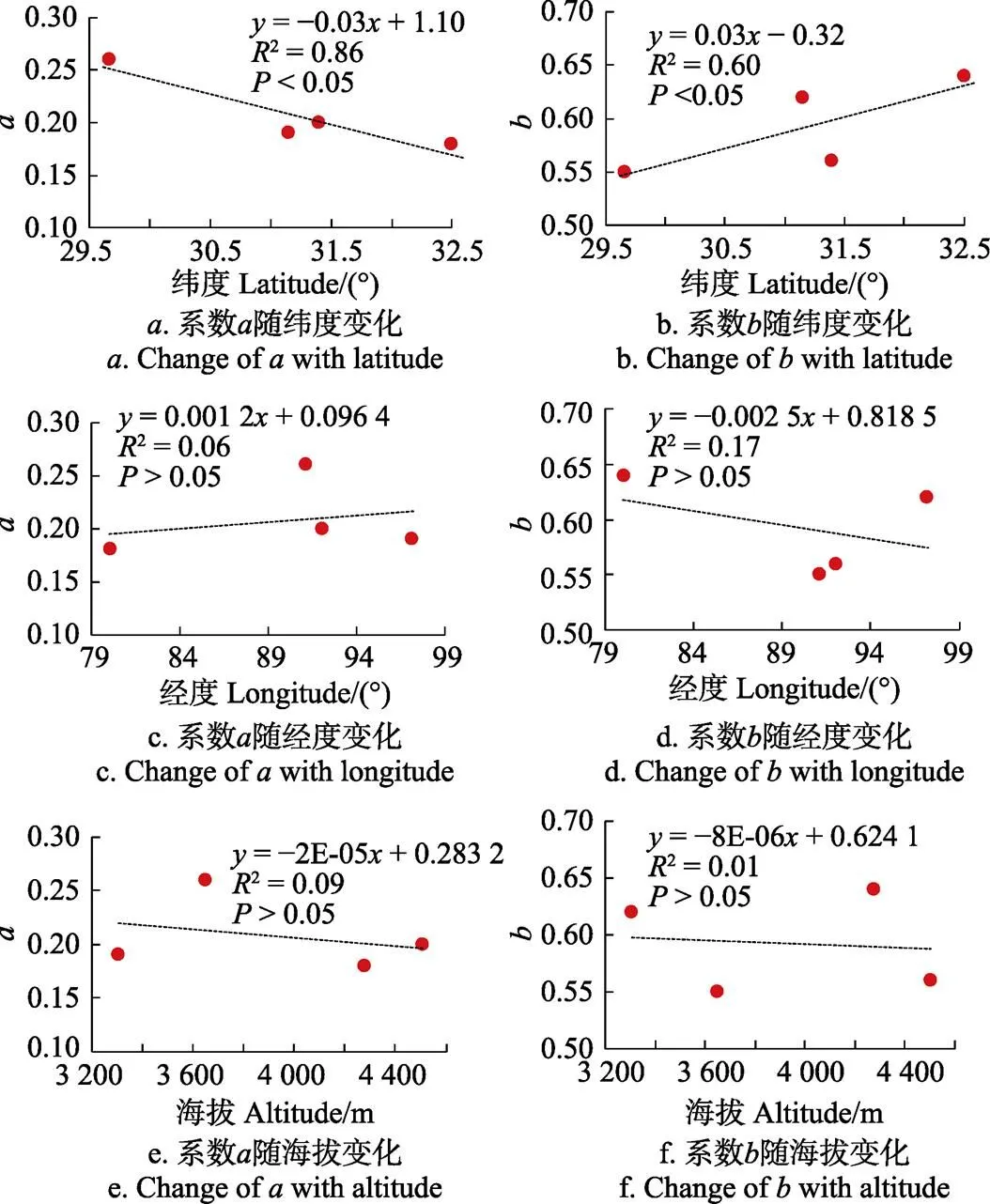
图4 AP系数率定值与经纬度及海拔的关系

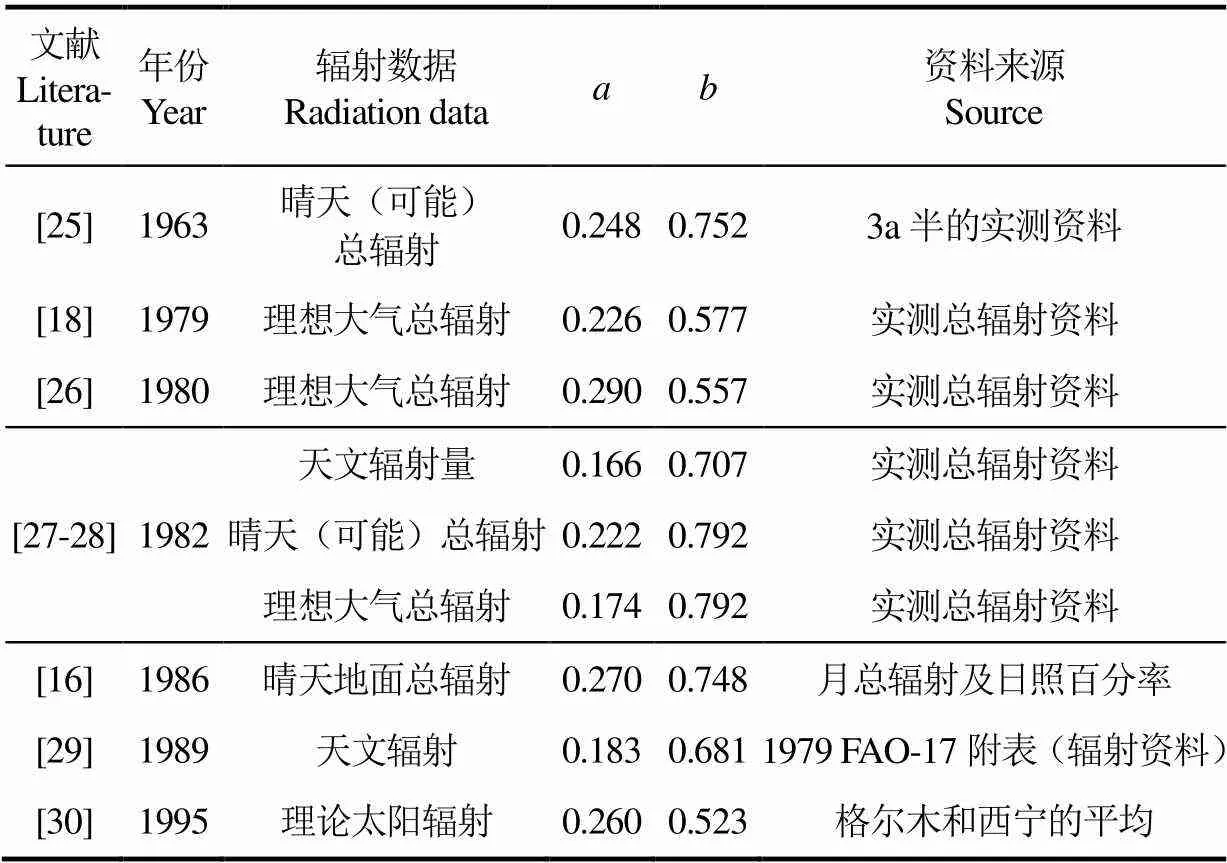
表4 Ångström-Prescott系数在青藏高原区的部分取值结果

2.3 AP模型系数农业区划结果

根据西藏4个辐射站的实测资料，率定出拉萨、狮泉河、那曲、昌都典型站点的、值。由于地理条件和气候条件不同，不同地区应分别采用不同的系数、，考虑西藏特殊的地理、气候条件以及辐射观测站点少，为此需通过区划来推求、系数。林芝、日喀则以及索县地区无辐射观测资料，无法直接由公式获得、值。根据前文所述的参数与纬度的相关性，选择4个实测站点作为参照站，进行基于纬度的反距离加权插值求取林芝、日喀则以及索县的、值（表5）。

西藏各农业区划、值结果如表6所示。在高原温带半湿润区，采用林芝站点作为该区域代表站，即采用=0.25，=0.55；在高原温带半干旱区，采用拉萨、昌都以及日喀则3个站点、值的平均值作为代表值，即采用=0.24，=0.57；高原温凉半湿润区，以索县的、值作为代表值，即=0.19，=0.61；高原温带干旱区，采用狮泉河实测辐射数据站点率定值作为代表值，即=0.18，=0.64；高原寒带干旱区，采用那曲实测辐射数据站点率定值作为代表值，即=0.20，=0.56。可以看出，除高原温带半湿润区，FAO推荐系数值总体偏高，而推荐系数则总体偏低。FAO推荐值在高原温带半湿润区的适用性最好，在高原温带半干旱区的适用性较好，误差在5%以下，而在其他3个农业区的适用性则较差。

表5 西藏其他典型站点a和b值

表6 西藏5个农业分区a和b值

3 结 论

本文基于拉萨、狮泉河、那曲、昌都站4个站点日总辐射及日照时数数据，探究了 Ångström-Prescott公式参数、值在西藏地区的选取，结论如下：

1）拉萨、昌都、那曲、狮泉河4个站点参数的率定值分别为0.26、0.19、0.20以及0.18，参数的率定值分别为0.55、0.62、0.56以及0.64。FAO的推荐值并不完全适用于西藏地区。

2）Ångström-Prescott系数、受纬度影响最为显著，其次是经度，与海拔高度无明显相关性。系数随纬度增加而减小，系数随纬度的增加而增大，但系数受纬度的影响较系数受纬度的影响更为明显。

3）4个站点计算值的精度在可接受的范围内，验证期4个站点SD值在1.75～2.80 MJ/(m2·d)之间，MAE值的变化范围为1.27～2.03 MJ/(m2·d)，MAPE值较接近0或稍有偏离。

4）在4个实测站点的基础上对林芝、日喀则以及索县地区的、值进行推算，进而根据西藏农业区划，确定高原温带半湿润区、高原温带半干旱区、高原温凉半湿润区、高原温带干旱区和高原寒带干旱区的、取值的变化范围分别为0.18～0.25和0.55～0.64。FAO的推荐值在高原温带半湿润区以及高原温带半干旱区适用性较好。该结果有利于太阳总辐射R的准确计算，并为西藏各地区ET0的精确估算和水资源的规划利用提供了科学依据。

[1] Akarslan E, Hocaoglu F O, Edizkan R. Novel short term solar irradiance forecasting models[J]. Renewable Energy, 2018, 123: 58－66.

[2] Aladenola O O, Madramootoo C A. Evaluation of solar radiation estimation methods for reference evapotranspiration estimation in Canada[J]. Theoretical & Applied Climatology, 2014, 118(3): 377－385.

[3] Liu Xiaoying, Mei Xurong, Li Yuzhong, et al. Calibration of the Ångström-Prescott coefficients (,) under different time scales and their impacts in estimating global solar radiation in the Yellow River basin[J]. Agricultural & Forest Meteorology, 2015, 149(3): 697－710.

[4] Wu Yiping, Liu Shuguang, Yan Wende, et al. Climate change and consequences on the water cycle in the humid Xiangjiang River Basin, China[J]. Stochastic Environmental Research & Risk Assessment, 2016, 30(1): 1－11.

[5] Rezaei E E, Gaiser T, Siebert S, et al. Combined impacts of climate and nutrient fertilization on yields of pearl millet in Niger[J]. European Journal of Agronomy, 2014, 55(2): 77－88.

[6] Sabziparvar A A, Movahedi S, Asakereh H, et al. Geographical factors affecting variability of precipitation regime in Iran[J]. Theoretical & Applied Climatology, 2015, 120(12): 367－376.

[7] Allen R G, Pereira, L S, Raes D, et al. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements[M]. Rome: FAO Irrigation and Drainage Paper 56, 1998.

[8] Mohammadi K, Khorasanizadeh H, Shamshirband S, et al. Influence of introducing various meteorological parameters to the Ångström-Prescott model for estimation of global solar radiation[J]. Environmental Earth Sciences, 2016, 75(3): 219.

[9] Benmouiza K, Cheknane A. Forecasting hourly global solar radiation using hybrid k -means and nonlinear autoregressive neural network models[J]. Energy Conversion & Management, 2013, 75(5): 561－569.

[10] 毛洋洋，赵艳霞，张祎，等. 五个常见日太阳总辐射模型在华北地区的有效性验证及分析[J]. 中国农业气象，2016，37(5)：520－530. Mao Yangyang, Zhao Yanxia, Zhang Yi, et al. Validation and analysis of five general daily solar radiation estimation models used in Northern China[J]. Chinese Journal of Agrometeorology, 2016, 37(5): 520－530. (in Chinese with English abstract)

[11] Samanta S, Patra P K, Banerjee S, et al. Generation of common coefficients to estimate global solar radiation over different locations of India[J]. Theoretical & Applied Climatology, 2018(2): 1－11.

[12] Akinoǧlu B G, Ecevit A. Construction of a quadratic model using modified Ångstrom coefficients to estimate global solar radiation[J]. Solar Energy, 1990, 45(2): 85－92.

[13] Liu Xiaoying, Mei Xurong, Li Yuzhong, et al. Evaluation of temperature-based global solar radiation models in China[J]. Agricultural & Forest Meteorology, 2009, 149(9): 1433－1446.

[14] Bristow K L, Campbell G S. On the relationship between incoming solar radiation and daily maximum and minimum temperature[J]. Agricultural & Forest Meteorology, 1984, 31(2): 159－166.

[15] Thornton P E, Running S W. An improved algorithm for estimating incident daily solar radiation from measurements of temperature, humidity, and precipitation[J]. Agricultural & Forest Meteorology, 1999, 93(4): 211－28.

[16] 钟强. 青藏高原太阳总辐射的计算方法的讨论[J]. 高原气象，1986，5(3)：197－210. Zhong Qiang. Disscussions in the climatological methods of calculating the global solar radiation over the Qinghai-Xizang plateau area[J]. Plateau Meteorology, 1986, 5(3): 197－210. (in Chinese with English abstract)

[17] 李成方. 西藏高原太阳总辐射的计算及其分布[J]. 西藏农业科技，1980(4)：81－88. Li Chengfang. Calculation and distribution of total solar radiation in Tibet Plateau[J]. Tibet Journal of Agricultural Sciences, 1980(4): 81－88. (in Chinese with English abstract)

[18] 潘守文. 青藏高原太阳总辐射的计算方法[C]// 青藏高原气象科学实验文集(一).北京：科学出版社，1984：1－14.

[19] 杜军. 西藏农业气候资源区划[M]. 北京：气象出版社，2007.

[20] Ångström A. Solar and terrestrial radiation 19[J]. Mon Wea Rev, 1924, 52(8): 83.

[21] Prescott J A. Evaporation from a water surface in relation to solar radiation[J]. Trans R Soc Sci Austr, 1940(64): 114－125.

[22] 胡庆芳，杨大文，王银堂，等. Ångström公式参数对ET0的影响及FAO建议值适用性评价[J]. 水科学进展，2010，21(5)：644－652. Hu Qingfang, Yang Dawen, Wang Yintang, et al. Effects of Ångström coefficients on ET0estimation and the applicability of FAO recommended coefficient values in China[J]. Advances in Water Science, 2010, 21(5): 644－652. (in Chinese with English abstract)

[23] Paulescu M, Stefu N, Calinoiu D, et al. Ångström–Prescott equation: Physical basis, empirical models and sensitivity analysis[J]. Renewable & Sustainable Energy Reviews, 2016(62): 495－506.

[24] Wang C, Yue T, Fan Z. Solar radiation climatology calculation in China[J]. Journal of Resources and Ecology, 2014, 5(2): 132－138.

[25] 左大康，王懿贤，陈建绥. 中国地区太阳总輻射的空間分布特征[J]. 气象学报，1963(1)：80－98. Zuo Dakang, Wang Yixian, Chen Jiansui. Characteristics of the distribution of total radiation in China [J]. Acta Meteorologica Sinica, 1963(1): 80－98. (in Chinese with English abstract)

[26] 王炳忠，张富国，李立贤. 我国的太阳能资源及其计算 [J]. 太阳能学报，1980(1)：5－13. Wang Bingzhong, Zhang Fuguo, Li Lixian. Solar energy resources in China[J]. Acta Energiae Solaris Sinica, 1980(1): 5－13. (in Chinese with English abstract)

[27] 祝昌汉. 再论总辐射的气候学计算方法(一)[J]. 南京气象学院学报，1982(1)：15－24. Zhu Changhan. A further discussion on the climatological calculating method of total radiation[J]. Transactions of Atmospheric Sciences, 1982(1): 15－24. (in Chinese with English abstract)

[28] 祝昌汉. 再论总辐射的气候学计算方法(二)[J]. 南京气象学院学报，1982(2)：196－206. Zhu Changhan. A further discussion on the climatological calculating method of total radiation (Ⅱ)[J]. Transactions of Atmospheric Sciences, 1982(1): 196－206. (in Chinese with English abstract)

[29] 童宏良. 我国蒸发力计算的气候学方法[J]. 南京气象学院学报，1989(1)：19－33. Tong Hongliang. A climatic calculation method for the evaporation power in China[J]. Transactions of Atmospheric Sciences, 1989(1): 19－33. (in Chinese with English abstract)

[30] 陈玉民，郭国双. 中国主要农作物需水量等值线图研究[M]. 北京：中国农业科技出版社，1993.

[31] 翁笃鸣. 试论总辐射的气候学计算方法[J]. 气象学报，1964(3)：54－65. Wang Duming. Discussion on the climatological calculation method of total radiation[J]. Acta Meteorologica Sinica, 1964(3): 54－65. (in Chinese with English abstract)

Study on parameter selection of Ångström-Prescott in Tibet agricultural region

Luo Hongying1,2, Li Dan2, Cui Yuanlai2, Tian Zhengye1, Luo Yufeng1,2

(1.860000; 2.430072,)

In Tibet, radiation stations are scare. The radiation is important for accuracy estimation of reference evapotranspiration. In this study, the parameters of typical Ångström-Prescott (AP) equation were estimated and FAO recommended values were evaluated for its applicability in Tibet agricultural region. The data of daily solar radiation and sunshine hours from 1961 to 2016 were from all the 4 radiation stations (Lhasa, Shiquanhe, Nagchu and Chamdo stations) in Tibet. The AP parameters were fitted by nonlinear least square method. The data from the years of 1961 to 2004 were for calibration and those from the year of 2005 to 2016 were for validation. Standard deviation (SD), mean absolute error (MAE) and mean absolute percentage error (MAPE) were used for model accuracy evaluation in order to find the main factor affecting parameter change. In addition, the relationships between parameters and longitude, latitude and altitude were analyzed. The stations were in 2 climatic regions of plateau temperate semi-arid zone and plateau cold arid zone. According to the, 5 zones were classified in Tibet, which included plateau temperate semi-humid zone, plateau cold arid zone, plateau temperate semi-arid zone, plateau warm-cool semi-humid zone and plateau temperate arid zone. Representative stations were chosen for these zones. Nyingchi, Shigatse, Suo county, Shiquanhe and Nagchu were for plateau temperate semi-humid zone, plateau temperate semi-arid zone, plateau warm-cool semi-humid zone, plateau temperate arid zone and plateau cold arid zone, respectively. Based on the relationship between main factor and parameters, the parameters for the other 3 zones were estimated by using inverse distance weighted method. The deviations from FAO recommended values were used for evaluation of FAO recommendations. The results showed that the SD, MAE and MAPE were in the acceptable range and the validation results for SD and MAE were 1.75-2.80 MJ/(m2·d), 1.27-2.03 MJ/(m2·d), respectively. The MAPE was closer or slightly different from 0. It indicated that the AP model was reliable for estimation of radiation. The calibrated coefficientsfor these 4 stations ranged from 0.18 to 0.26 and from 0.55 to 0.64, respectively. The recommended values by FAO were not always suitable in Tibet with the deviation of -28%-28%. The coefficient of variation of coefficient recommended by past studies was 15%-20%. Compared to previous studies with shorter time period, our results were more reliable since the time duration (about 50 years) was longer. The parameters were closely correlated with latitude with the determination coefficient higher than 0.6 but they were less related with longitude and altitude with the determination coefficient less than 0.2. Based on latitude, the interpolation was conducted for Nyingchi, Shigatse and Suo county. Finally the AP coefficients for 5 different agricultural zones were obtained and they ranged from 0.18 to 0.25 and from 0.55 to 0.64, respectively. The deviation analysis showed that the FAO recommended values had a good applicability in the plateau temperate semi-humid zone, plateau cold arid zone and plateau temperate semi-arid zone. The results can provide valuable information for the calculation of solar radiation and reference evapotranpiration in the areas without measured radiation data in Tibet.

radiation; altitude; latitude; Ångström-Prescott equation; Tibet; parameter estimation

罗红英，李 丹，崔远来，田正野，罗玉峰. 西藏农业区Ångström-Prescott公式参数选取研究[J]. 农业工程学报，2019，35(3)：149－155. doi：10.11975/j.issn.1002-6819.2019.03.019 http://www.tcsae.org

Luo Hongying, Li Dan, Cui Yuanlai, Tian Zhengye, Luo Yufeng. Study on parameter selection of Ångström-Prescott in Tibet agricultural region[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(3): 149－155. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.03.019 http://www.tcsae.org

2017-12-19

2019-01-01

国家自然科学基金项目（51769035）；西藏自治区科技厅地区自然科学基金项目（ZH20170006）；西藏农牧学院2015年柔性引进人才项目；西藏自治区第三批重点科技计划项目经费资助

罗红英，门巴族，副教授，主要从事节水灌溉方向及动力的研究和教学。Email：lhy_xz@sina.com

10.11975/j.issn.1002-6819.2019.03.019

P351.3

A

1002-6819(2019)-03-0149-07