基于MFC前馈补偿的抛物面天线型面控制方法

孙国钟，孙士勇，裴英博

(大连理工大学 机械工程学院，辽宁 大连 116024)

0 引言

抛物面天线利用电磁波来传递信息和能量，通过利用抛物面的反射特性，可以将接受的信号集中到主焦馈源上，从而使抛物面天线具有集中信号、增强信号等优势，在远程通信、军用民用航天航空、定位导航、精密机械等领域具有广泛应用[1-3]。

大型抛物面天线对自身结构精度有严格要求，系统要求大尺寸抛物面天线只有毫米级变形。然而，在抛物面天线加工以及服役过程中都会因为外界因素而产生变形，这些表面形变都会使抛物面天线的信号强度降低，影响使用[4]。

传统抛物面天线设计思路是通过提高结构刚度减少变形，但随着天线尺寸增加精度提高， 采用智能材料对抛物面天线面型精度进行控制已成为国内外研究热点。Wastington[5]研究出一种抛物面“单弯曲”天线，采用压电陶瓷致动器，这种天线通过固粘于天线反射表面的压电材料施加电压来改变天线的形状。Yoon等[6]研制了“双弯曲”压电陶瓷带状驱动孔径天线。上述研究工作均采用有限元法进行数值分析，能够对智能材料驱动效能进行预测,但未完全解决提高抛物面天线控制精度的问题。

针对抛物面天线在服役过程中会因为自身制造误差及环境因素而影响型面精度的问题，本文采用有限元法设计制造了含压电纤维执行器(MFC)的抛物面天线，通过控制测量平台获得MFC致动下的抛物面天线变形响应，基于前馈补偿算法，提高了MFC控制精度。

1 MFC致动下的抛物面天线仿真分析

1.1 有限元模型的建立

MFC致动力有限，因此在控制试验前，采用有限元法对抛物面天线基本构型和变形特征进行评估，为天线制造提供基础。

基于热弹性比拟法，在ANSYS中建立含有MFC的复合材料抛物面天线有限元模型，将MFC区域单独划分出来，根据热弹性比拟法分别赋予复合材料和MFC材料性质[7]。MFC和复合材料天线满足位移连续条件，不考虑粘接层的厚度影响。因为本文主要研究MFC控制抛物面天线变形及控制过程中的精度问题，因此，未探讨MFC贴片的位置的最优化问题。有限元模型如图1所示。

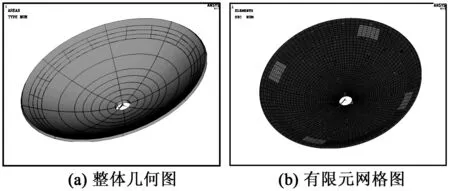
图1 有限元模型

1.2 仿真结果分析

仿真过程中，分别在4个象限相同位置布置4片P1类型MFC对抛物面天线进行控制，对4片MFC施加不同正、负电压和相同电压的情况下获得仿真分析结果如图2所示。

图2 MFC对抛物面天线的控制仿真分析

由图2可知，对P1类型MFC施加正电压将发生伸长变形，负电压下MFC发生压缩变形，因此，施加不同正、负电压会使结构呈现不同的变形特征，即可根据天线实际误差，采用不同的正、负电压来获得不同的面型精度控制。

2 MFC致动下的抛物面天线试验

2.1 抛物面天线模型的制造

基于仿真分析结果确定的天线几何特征，采用玻璃纤维复合材料和接触成型工艺制造抛物面天线，将玻璃纤维依次分块逐层铺放到模具上，之后放入温度箱固化成型天线和背面加强筋。

抛物面天线制备完成后，根据仿真结果，按照设计位置在天线背部粘接压电纤维执行器。最后将抛物面天线进行脱模，中心部分采用金属接头固定在试验台上，进行后期控制试验。

2.2 试验设备与步骤流程

试验设备及软件：激光位移传感器、直流电源、数据采集卡、压电纤维执行器、电压放大器、计算机、LabVIEW。地面试验示意图如图3所示

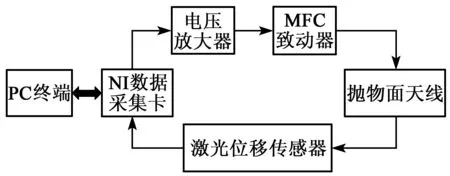
图3 地面试验示意图

2.3 试验结果分析

控制采用正弦信号输入，MFC有效输入电压为-500～+1 500 V，为了研究MFC控制变形的能力与输入电压幅值的关系，采用多组幅值输入电压进行试验。输入的正弦电压幅值从40 V开始以40 V的递增方式到400 V为止，共进行10组试验，其中选取代表性的幅值为160 V和400 V的正弦电压数据，图4为天线位移与输入电压关系图。

图4 幅值为160 V、400 V时抛物面天线位移-电压图

由图4可知，在MFC致动下通过激光位移传感器测得的天线位移与输入电压呈近似线性变化，从而确定系统的可控制，但仍具有一定的迟滞性，影响系统的控制精度。

3 前馈补偿控制算法设计

目前，采用MFC控制抛物面天线型面精度的研究较少，且多采用闭环控制，相对于闭环控制需要位移传感器进行数据采集反馈；采用开环控制系统，只需对抛物面天线进行建模、前馈控制，更具有现实意义。本文利用开环前馈补偿控制进行MFC控制，采用现象模型中的改善补偿迟滞模型进行试验，其建模参数与迟滞的物理实质之间无任何关系，只考虑输出、输入之间的关系。

MPI模型是在PI模型基础上进行的改进。PI模型使用有限具有不同阈值的Play算子的加权叠加来表征迟滞特性[8]。Play算子如图5所示。其定义如下：

y(t)=Hrh[x,y0](t)=

max{x(t)-rh,min{x(t)+rh,y(ti)}}

(1)

式中：x(t)为单调区间t0～tn上的单调分段输入信号；rh∈R+为Play算子的阈值；y0∈R为独立算子的初始值。

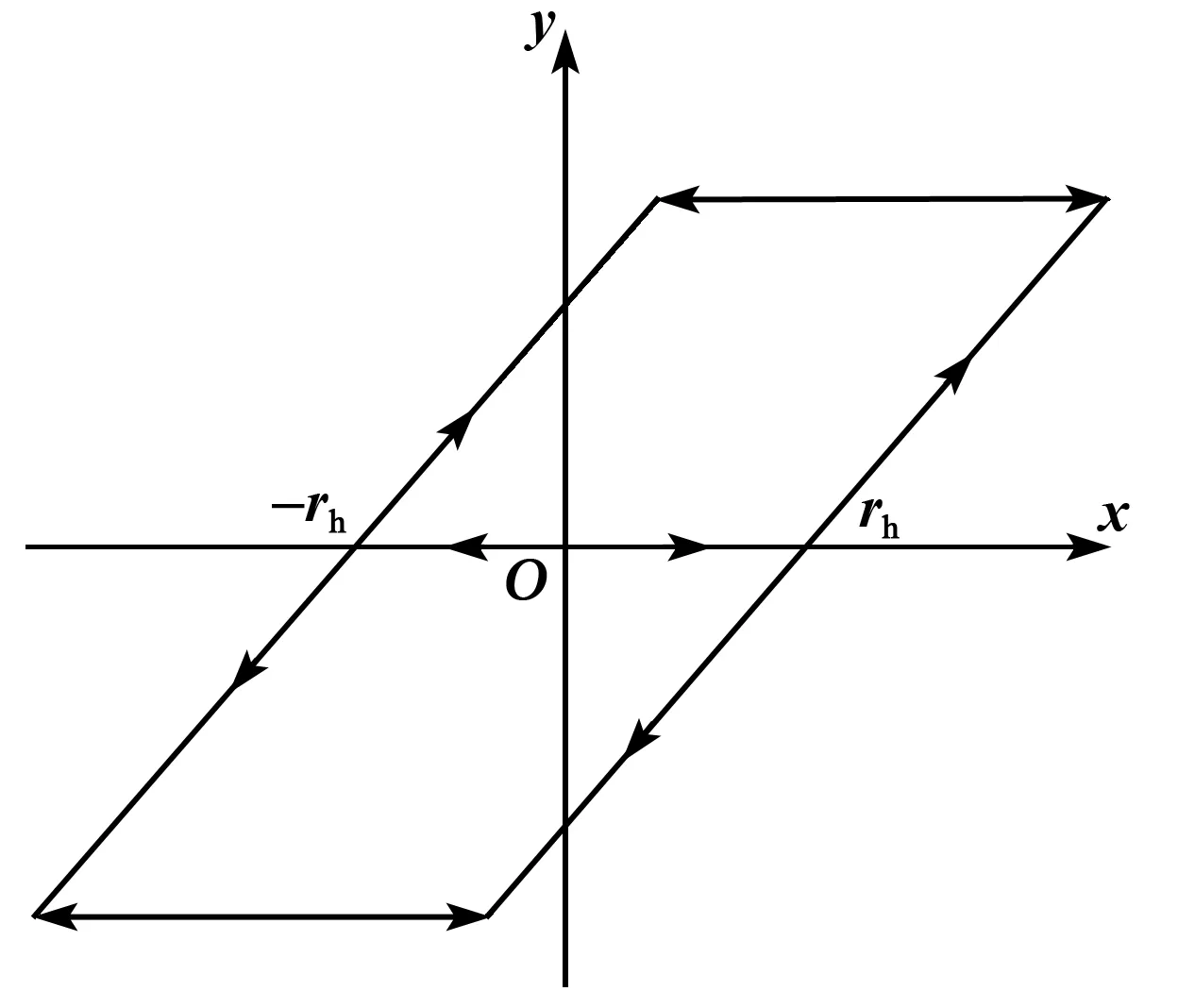
图5 Play算子函数

PI模型表达式为

(2)

式中:wh=[wh0,…,whn]T为权值向量;rh=[rh0,…,rhn]T为阈值向量；y0=[y01,…,y0n]T为Play算子初始值向量。

MPI模型是在PI模型的基础上串联不同阈值的单边死区算子的加权叠加，从而能够描述大多数压电驱动器的非对称和非凸性的迟滞环。单边死区算子如图6所示，其定义如下：

Srs[y(t),rs]=

(3)

式中rs∈R为单边死区算子的阈值。

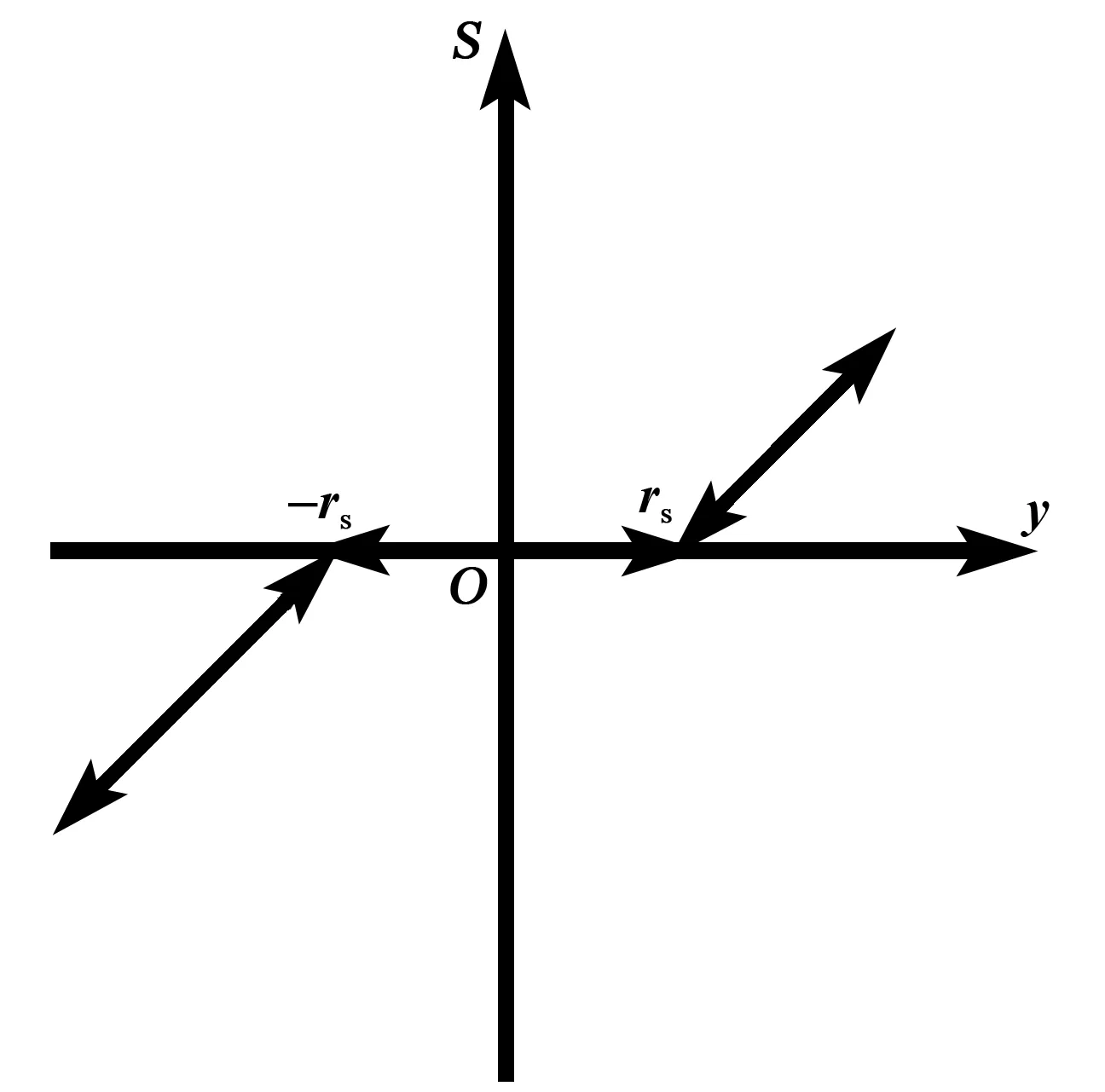
图6 单边死区算子

具有不同阈值的单边死区算子的加权叠加可以表示为

(4)

(5)

为了确定迟滞补偿函数模型，必须先确定计算出迟滞性函数模型，然后根据迟滞性函数模型，来确定补偿模型。迟滞性函数输出用φ来表示，输入用rH来表示，即迟滞性函数为

(6)

且满足

(7)

有了迟滞性函数，可以计算出迟滞补偿逆函数。

根据补偿函数和传递函数关系可知，它们互为逆函数，也可以近似构造补偿函数：

(8)

而根据逆函数的定义，可知：

(9)

利用式(9)可以将得到的传递函数求出传递补偿逆函数。 最终迟滞性函数图像与迟滞补偿逆函数图像如图7所示。

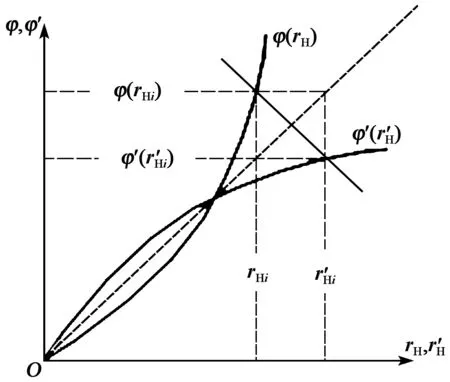
图7 迟滞性传递函数和补偿函数示意图

由于MFC存在迟滞特性，因此，若要在开环中实现精确的变形控制，就必须考虑迟滞特性的影响。综合分析系统特性，可将抛物面天线控制模型表示为迟滞模型。在该系统模型中，输入一组正弦信号，然后信号进入迟滞逆补偿模型，将控制信号先进行补偿，然后将补偿后的信号输入迟滞模型，最后输出线性信号，以输入电压400 V幅值为例，此时补偿后的结果和仿真结果对比如图8所示，二者符合良好。补偿结果表明，利用迟滞前馈补偿法可提高MFC对抛物面天线的控制精度。

图8 考虑迟滞性模型MFC前馈补偿控制与仿真结果对比

4 结论

通过模拟仿真和控制补偿研究了抛物面天线的控制精度问题，得到以下结论：

1) 基于热弹性比拟法可在有限元软件中模拟MFC的致动性能，并对抛物面天线的构型进行设计，不同的输入电压幅值和正、负电压可获得不同的天线控制效果，可为MFC的布置方案设计和控制试验提供基础。

2) 搭建了MFC致动下的抛物面天线控制试验平台，在MFC致动下天线位移呈现迟滞性，影响控制精度。

3) 建立MPI迟滞性模型，采用前馈补偿控制法，可将抛物面天线控制位移线性化，从而提高控制精度。