去伪存真 等价求证——2017全国卷Ⅲ客观题第12题的解法思考

甘肃省兰州市永登县第二中学 (邮编：730302)

2017年全国卷第3卷客观题第12题是一道压轴好题，题目设置精巧，科学合理，考查学生数学思维的深刻性，广阔性，批判性，敏捷性.如果考生没有深入的思考和探究，就会犯一些难以察觉的错误.本文通过该题的一个典型错解分析，借以澄清认识，厘清数学思维，提高考生数学思维能力和数学素养.

1 错解思维过程

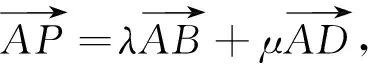
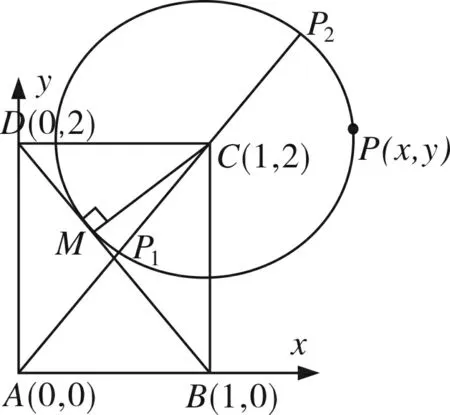
图1

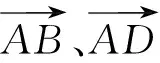
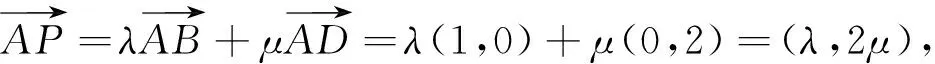
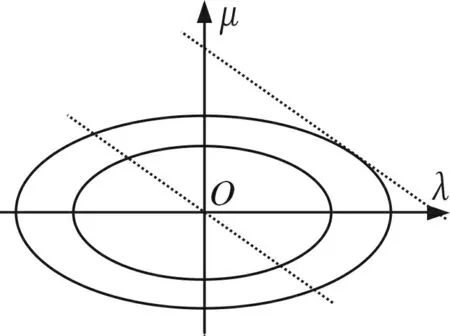
图2

然后利用线性规划来求目标函数的最大值.

令t=λ+μ，当t=0时，目标等值线l0:λ+μ=0,即μ=-λ,平移l0:λ+μ=0到l:λ+μ=t使得l与椭圆环外边界相切时，t可取得最大值.

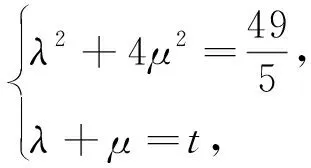
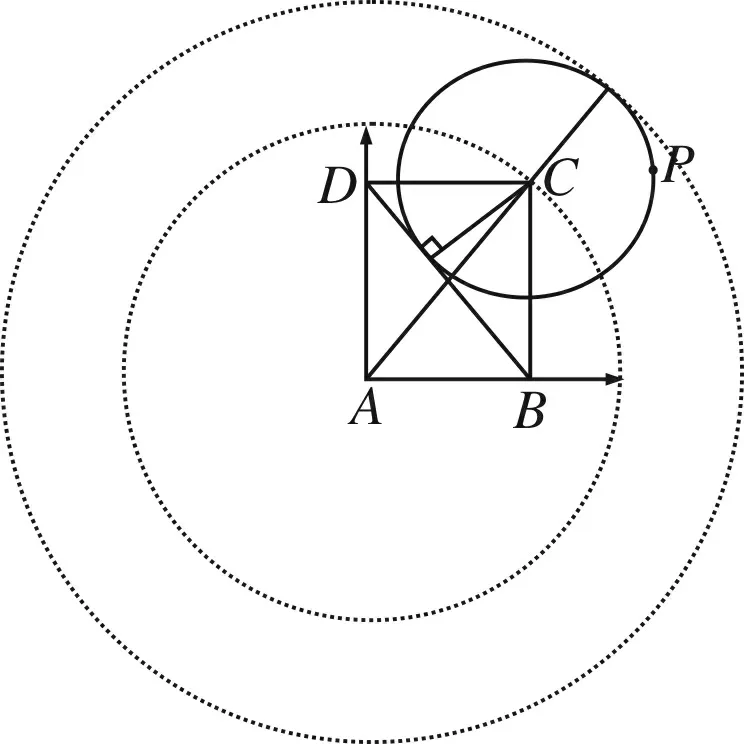
图3

2 错因分析

这个典型错解几乎可以混淆真解，是个似真的伪解.只有用深厚的数学功力练就数学“火眼金睛”，才会识破伪装，获得数学本真.

3 正解展示

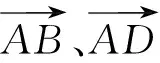
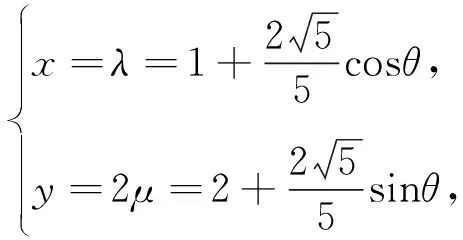
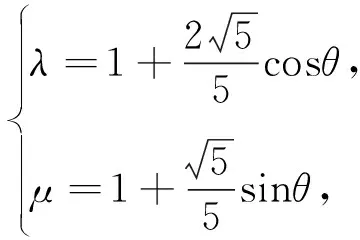
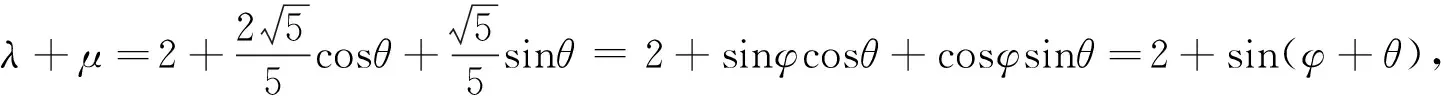
上述解题过程中，参变量范围等价，解题过程等价，故此解法为正解.

数学命题的等价正是源于数学的等价思想，保证了命题的真值性，也就保证了数学的完整性和科学性.类似于物理学中的能量守恒定律，数学研究的是数学问题解决过程中，参与的变量保证等价转换，物理学探讨的是物体形态变化中，能量形式变化，但在转化和转移过程中，其总量不变.

4 变式拓展

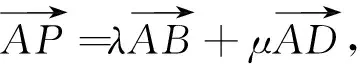
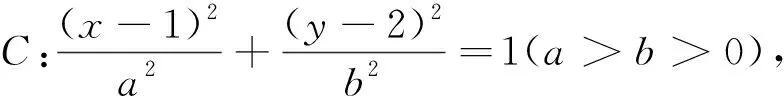
其中θ∈[0,2π)，

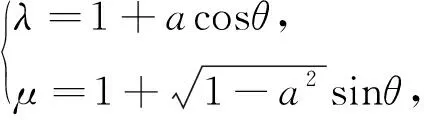
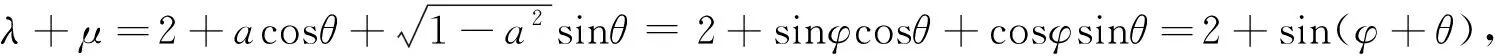
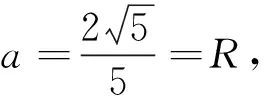
5 本质挖掘

事实上，由平面向量基本定理知道，平面内任意一个向量都可以表示为两个不共线向量的线性组合.因而，将这两个不共线向量作为一对基底，可以建立平面仿射坐标系.在仿射坐标系下的整个仿射过程中，平行性不变.我们可以利用这个性质来解决第12题.

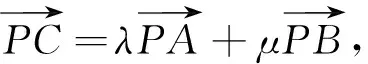
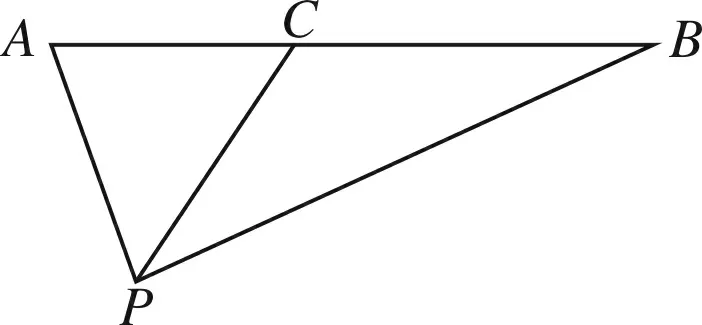
图4

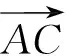
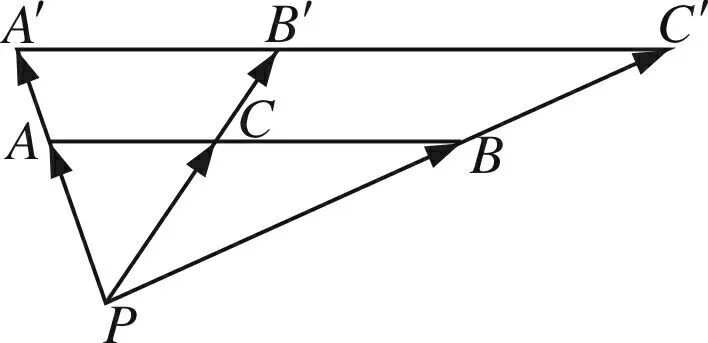
图5

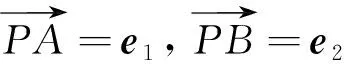
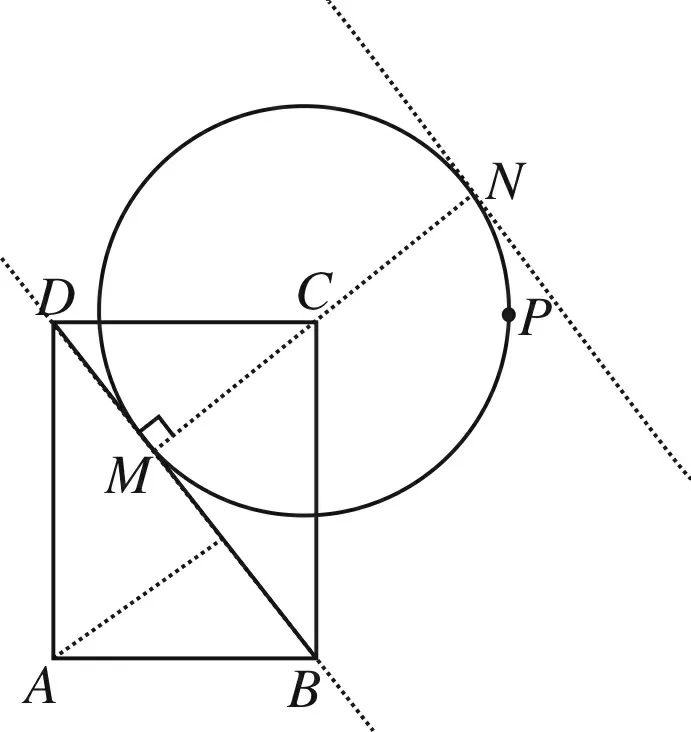
图6

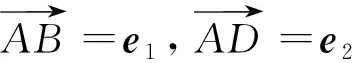
综上知，当目标等和线扫过整个圆C，达到两个相切位置时，即当点P运动到两个点M、N时，λ+μ分别取得最小值和最大值，即(λ+μ)min=1,(λ+μ)max=3.