巧结合大作用：函数思想的构造应用

江西省南昌市莲塘第一中学 (邮编：330200)

高中阶段数学思想主要有四个：函数与方程思想、数形结合思想、分类讨论思想、化归转化思想.也是新课改中数学核心素养的主体，高考就是围绕以考查考生对数学思想的理解与掌握为重心，高考试题中经常出现一类函数题， 常常采用函数与方程思想构造函数法解答能起到优化解题思路，提升思维的效果.一般在抽象函数中出现了含有函数导数符号的不等式或等式时，在解题思路上可以从构造函数来解决问题，可以得到较快捷的解题思路，体现了函数思想在与方程及不等式的巧妙结合获得的大作用.本文就此做一这方面的探讨.

1 条件中含f′(x)的不等式的题型

含f′(x)的不等式时，一般结合所给不等式进行变形，两边同乘或同除某个式子，比如x、x2、ex、(ex)2或某个抽象函数符号.再由所构造的函数形式求导以判定构造出来的函数的单调性解决问题.

题2在数列{an}中，(an)n+1=n+1,(n∈N*).则数列{an}中的最大项为( ).

易得a1a3>a4>…….

猜想当n≥2时，{an}是递减数列.

故当x≥3时，lnx>1，则1-lnx<0，即f′(x)<0.

故f(x)在[3,+∞)内为单调递减函数，

2 条件中含f′(x)的等式的题型

含f′(x)的等式时，也是先一般结合所给条件等式，进行变形，也是两边同乘或同除某个式子比如x、x2、ex、(ex)2或某个抽象函数符号.但是因为是等式，不像前面给出的是含f′(x)不等式，更容易判定单调性解决问题.构造完后，还需要进一步结合表达式本身特征来分析再构造讨论函数性质.

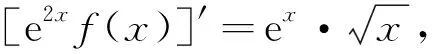
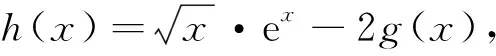
即有f′(x)≤0，则函数f(x)在[0，+∞)上为减函数；

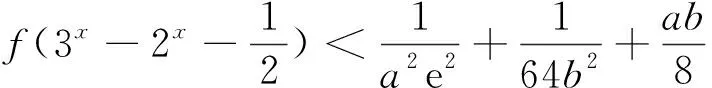
3x-2x-1>0.

解可得x>1，则不等式的解集为(1，+∞).

所以f′(x)≤0，即f(x)在[0,+∞)上单调递减.

所谓构造函数法是指通过一定方式，设计并构造一个与有待解答问题的相关函数，并对其进行观察分析，借助函数本身性质如单调性或利用运算结果，解决原问题.构造本身非常巧妙地把函数与方程、函数与不等式联系起来，既考查到考生对数学知识的掌握，也考查到了考生处理数学问题的能力，符合高考新课标的要求.