估算方法的探究与思考
——以2018年高考浙江卷第22题为例
浙江省温州市龙湾区永强中学 (邮编:325000)
2018年高考浙江卷第22题的第2问为:
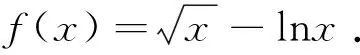
(2)若a≤3-4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
官方给出的参考答案如下:
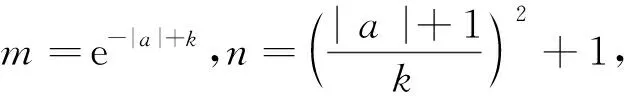
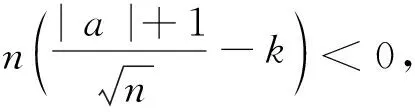
因此,对于任意的a∈R及k∈(0,+∞),直线y=kx+a与曲线y=f(x)有公共点.
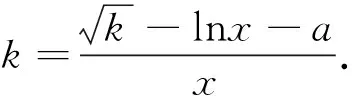
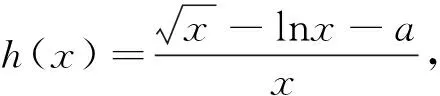
由(Ⅰ)可知g(x)≥g(16),又a≤3-4ln2,故-g(x)-1+a≤-g(16)-1+a=-3+4ln2+a≤0,所以h′(x)≤0,即函数h(x)在(0,+∞)内单调递减,因此方程f(x)-kx-a=0至多有1个实根.
综上,当a≤3-4ln2时,对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
这道题的思路比较明确,就是先用零点存在定理证明零点的存在性,然后利用单调性确定零点的个数,其中一个难点在于估算零点的所在区间.
估算零点的所在区间,端点效应和端点分析,是在很多高考函数题的分析过程中,需要做的预处理,因此,这些点的寻找,对于快速地解题大有裨益.
1 估算零点的核心思想
既然要估算零点的所在区间,前提是零点存在.如果要快速有效的找点,极限思想可以确保对点的存在性的准确判断.
从最简单的问题出发:取一点使得x>0.这个是取点中最简单的问题,但是最简单的问题,恰恰能反映出问题的本质.拿到这个不等式,很多人的第一反应是任意的正数都符合题意,当然这个是正确的,其原因是最关键的零点x=0被我们抓到了,因此,若遇到函数零点可以直接求解,这样的取点是非常容易的.但是在实际操作过程中,我们不仅会遇到零点不可求,甚至还会含参函数的取点.
进一步再作思考:取点使f(x)=alnx+x-a2>0.在取点之前,先用极限来确保我们要的点存在:当x→+∞时,高阶的x占主导,因此保留下来,而低阶的alnx和-a2正负不会影响整体代数式的正负,可以舍去.这个过程可以简称为“取大舍小”.通过这个过程,可以确定的是:存在x使得f(x)=alnx+x-a2>0.
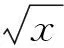
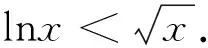
2 估算的关键:取点技巧
2.1 取大舍小
2.1.1 精准舍项
事实上,在上一节例题中笔者已经应用了这个技巧,如果在一个代数式f(x)+g(x)+h(x)>0中取点,代数式f(x)和g(x)都大于0,且f(x)的阶高于g(x)的阶,则可以把低阶的g(x)舍去,如果f(x)和g(x)都的阶都比h(x)高,则可以舍f(x)和g(x)中任意一项.舍项处理的原则是:其一,舍项后的式子仍然有比h(x)高的阶存在或者说整体代数式依然有我们要的点存在,可称之为保号性.其二,舍项后的代数式易于找点,例如:f(x)=ex+x2-ax,要取f(x)>0的最佳策略是舍去ex,因为舍去后易于找点.
2.1.2 界值限定
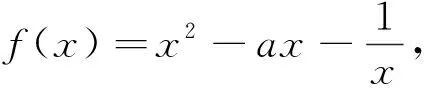
2.1.3 调整结构
其实在大多数题目中,没有什么问题是通过调整不能解决的.所谓调整结构我们依然要分两个维度来认知,其一,分而治之.这个方法对于乘积结构的式子特别好用,形如f(x)g(x)+h(x)>0的取点,若f(x)g(x)难以处理,我们可以将f(x)g(x)拆分,调整代数式结构来取点.例如2017年9月浙江省温州市普通高中适应性测试第20题:
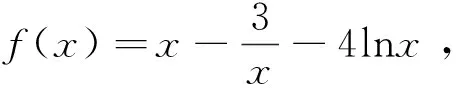
(1)求f(x)的单调递增区间;
(2)当0 所谓统一矛盾就是对于含不同形式混合型式子我们通过调阶的方法将不同形式的结构统一为可解的式子.具体操作就是通过找点不等式根据目标进行放缩,必要时可以介入一定的待定思想.原则上只要可解的式子就可以,但我们往往会把复杂结构统一为多项式.例如:(2017新课标1);f(x)=e2x+aex-x,取点使f(x)>0,则f(x)>e2x+aex-ex,这么做的目的就是统一矛盾,转化为可解的式子. 第一步 调整结构 先用极限判断一个代数式中各个部分的正负,整体的正负以及抓到这个式子中的高阶选手,并且明确我们要取点的区间的大致范围.如果结构复杂就去调整结构,有低阶无穷小优先舍项和限定区间. 第二步 赋特殊值 第三步 调阶放缩,统一矛盾 所以,存在x0∈(m,n),使f(x0)=kx0+a. 这里我们也可以做一个比较: 也就是说,根据这样的放缩技巧,可以取到比较理想的点,从而达到做题的要求. 又例如:2018年新课标II(理)第21题第(2)问:已知函数f(x)=ex-ax2. 若f(x)在(0,+∞)内只有一个零点,求a. 官方解答:设函数h(x)=1-ax2e-x. f(x)在(0,+∞)内只有一个零点当且仅当h(x)在(0,+∞)内只有一个零点. 故h(x)在(2,4a)内有一个零点,因此,h(x)在(0,+∞)内有两个零点. 官方解答中取x=4a时,使得h(x)>0.事实上,x的取值可以更加快速简洁,即由于,ex-ax2>ex-a>0⟹x>lna结合x∈(2,+∞),直接可以取x=2+lna,从而达到取点的目的. 这里需要补充的是,前文所提的主要是当x→+∞时的取值方法,而当x→0和x→-∞甚至是对于x→x0(x0为某一特定的实数)的取值方法,都有异曲同工之处,因此不再赘述. 本文介绍的估算方法不仅仅在使用零点存在定理时可以应用,事实上,对于大部分的解题,这样一种端点分析和不等式的思想都是不可或缺,也是锻炼学生思维的优良素材.其中蕴含的极限思想,在学生学导数时,就可以加以渗透,使学生对各类函数有一个全局性的认识,这对于学生解题方法的掌握,解题思路的拓宽,发散性思维的锻炼,都是大有裨益的.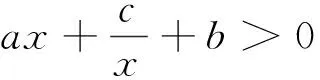
2.2 统一矛盾
3 估算的实践——逐步击破难点
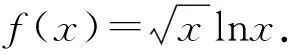
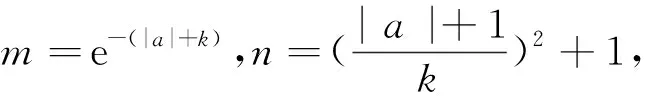
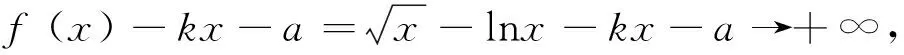
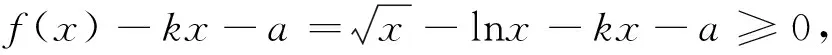
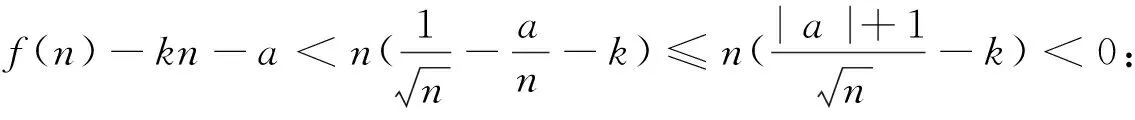
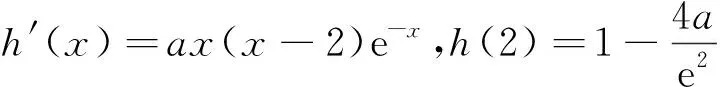
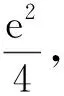
4 估算方法的启发与思考

