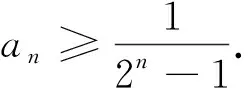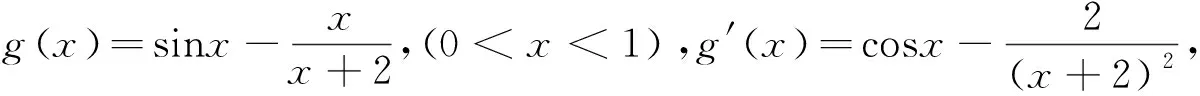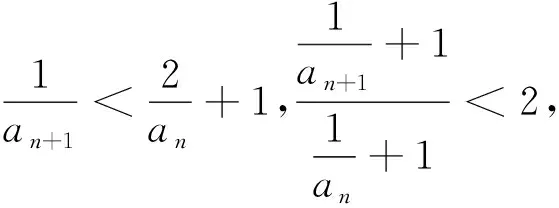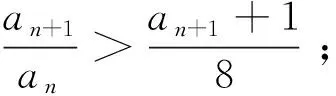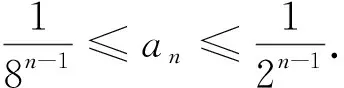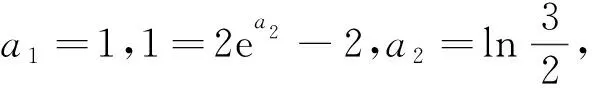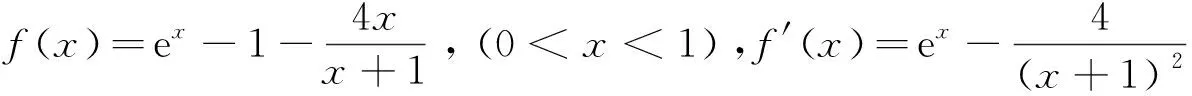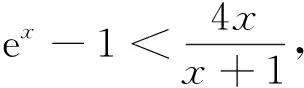2017年高考浙江理科卷压轴试题命题手法探究
福建省泉州第五中学 (邮编:362000) 福建省泉州实验中学 (邮编:362000)
研读2017年高考浙江卷的压轴试题,追根溯源,发现本题源自数列不动点的解题思想,将数列、函数、不等式等知识进行交汇,并从中提炼、设置问题.下面展示探究本题命题方法的思考过程,并根据此命题方法进行试题命制.
1 试题展示
题目(2017年高考浙江卷理科)已知数列{xn}满足x1=1,xn=xn+1+ln(1+xn+1)(n∈N*).
证明:当n∈N*时,
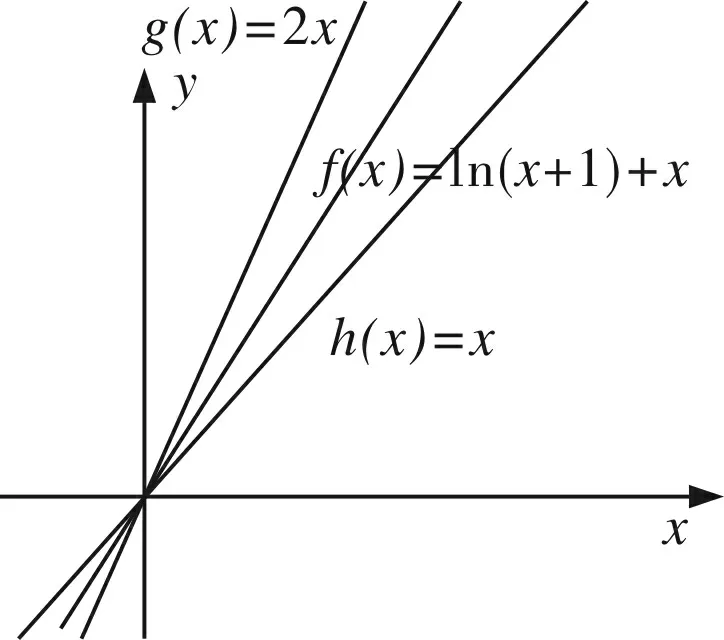
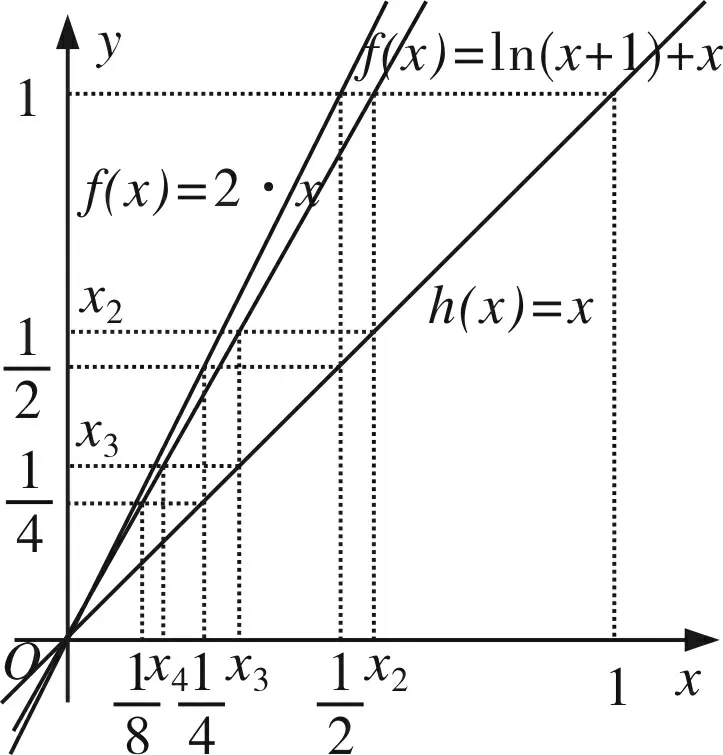
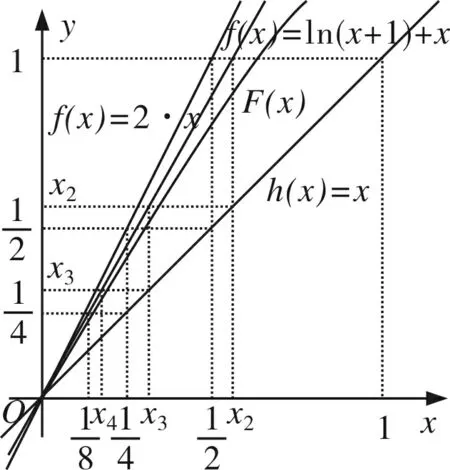
(Ⅰ)0 数列是特殊的函数,命题者考虑以函数为背景构造递推数列,并利用函数与导数来研究数列的性质,强调数列的本质. 第一步:确定函数解析式. 命题者先确定题干的函数背景. 指数函数和对数函数是高中阶段学习的两个重要的基本初等函数,是函数与导数题目中的热点函数模型;不等式x-1≥lnx、ex≥x+1更是教材的习题中证明过的一组不等式,命题者拟增加考查不等式x-1≥lnx的放缩应用(可以变形为x≥ln(x+1)),故确定函数模型f(x)=ln(x+1)+x. 第二步:确定递推数列,寻找不等关系. 接着,命题者构造数列{xn}满足递推关系xn=xn+1+ln(1+xn+1). 图1 由x≥ln(x+1),知当x>0时,x 图2 第三步:模拟学生解答. 下面证明问题(Ⅰ)“不等式0 图3 此题干的一个亮点就是数列递推关系是xn=f(xn+1)形式,且无法写成xn+1=g(xn),则导致无法从数列的前项推后项,只能由后向前推,故本问的证明宜采用反证法. 假设∃n0∈N*,使得xn0+1≤0,则xn0=xn0+1+ln(1+xn0+1) 第六步:不等式变形设置问题(Ⅱ). 经过上述步骤,便完成了2017年高考浙江理科卷压轴题的命制. 经历了上述试题的探究过程,我们掌握了试题的一种命题手法.应用同样的手法,我们可以进行试题的命制,下面笔者命制两个试题,供读者赏析. 新题1已知数列{an}满足a1=1,an+1=sinan,n∈N*.(附:sin1≈0.84.) 证明:(Ⅰ)0 (Ⅱ)an+1an>an-2an+1; 证明(Ⅰ)数学归纳法证明. 当n=1时,a2=sin1,显然0 假设当n=k时,原不等式成立,即0 f(x)=sinx-x,f′(x)=cosx-1≤0,所以f(x)递减,由ak+1>0,得f(ak+1)=sinak+1-ak+1 综上可得∀n∈N*,0 即an+1an>an-2an+1. 新题2已知数列{an}满足a1=1,an=2ean+1-2. 证明:(Ⅰ)0 证明(Ⅰ)数学归纳法证明. 假设当n=k时,原不等式成立,即0 当n=k+1时,由假设ak+1>0可知2eak+2-2>0,则eak+2>1,所以ak+2>0;函数y=2ex-2单调递增,若ak+2≥ak+1,则2eak+2-2≥2eak+1-2,即ak+1≥ak,与假设矛盾,故0 (Ⅲ)g(x)=ex-1-x,g′(x)=ex-1,当x∈(0,1)时,g′(x)≥0,g(x)递增,g(x)≥g(0)=0,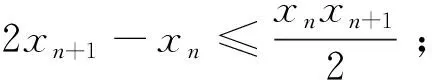
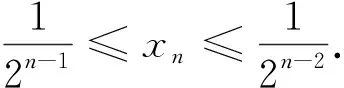
2 命题手法探究
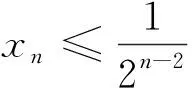
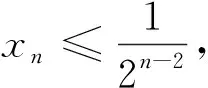
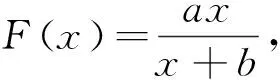
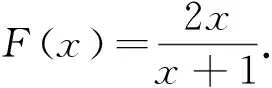
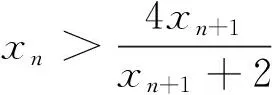
3 命制新题