变刚度Winkler地基上受压非均质矩形板的自由振动与屈曲特性

滕兆春， 衡亚洲， 崔 盼， 刘 露

(1. 兰州理工大学 理学院， 兰州 730050； 2. 江苏兴达钢帘线股份有限公司, 江苏 兴化 225721)

弹性地基上新型材料矩形板的静、动力学特性的研究在工程领域有十分重要的意义和广泛的应用背景。工程实际中常见的弹性地基虽然大都是均匀的，但也会遇到非均匀弹性地基的情况，例如建筑物的弹性地基变刚度调平设计、复合地基中的筏板基础和含填充物的弹性地基等。功能梯度材料(Functionally Graded Material，FGM)作为一种新型非均质先进复合材料[1]，对其研究如今已由最初的耐高温高热和应力缓和型材料逐渐扩大到机械、电子信息、航空航天、核工业、光学器件、生物、汽车以及土木工程等领域。目前的研究多集中在材料参数沿厚度方向变化的情况，给出了FGM结构在弯曲、振动、屈曲以及断裂等方面的响应，而对FGM板刚度面内变化的研究则很少[2-4]。求解非均质材料矩形板自由振动和屈曲问题的方法虽然较多，如有限单元法[5]、微分求积法[6-7]、样条法[8]、里兹法[9]、辛弹性方法[2]等，但是这些方法中有些需要较多的网格和和较大的前处理工作量以及计算量才能达到需要的精度，有的方法往往又需要繁琐的公式推导和较多的边界条件限制，给求解带来不便。

微分变换法(Differential Transform Method, DTM)是一种能有效将线性或非线性微分方程(组)变换成代数方程(组)求解的半解析方法[10]，最初被用来对电路中问题的分析[11]，近年来DTM也逐渐用于结构的静、动力学响应求解[12-21]，求解过程编程简单且具有较高的计算精度，所得结果完全能满足工程方面的要求。在DTM应用中，Lal等[22]采用DTM求解了轴对称功能梯度材料(FGM)圆板的无量纲固有频率和临界屈曲载荷，给出了与频率对应的前三阶振型。Shariyat等[23]采用DTM求解了双参数弹性地基上双向功能梯度材料圆板的自由振动和模态应力问题，给出了不同边界下受材料性质和地基刚度系数影响的固有频率和模态应力。Kumar[24-25]基于经典薄板理论，采用DTM分别分析了Winkler弹性地基上各向同性矩形板和Winkler弹性地基上晶体矩形板的自由振动，得出了不同边界下的前三阶无量纲固有频率和相应的振型。Semnani等[26]基于经典薄板理论，采用DTM分析了四边简支和四边固定边界下各向同性变厚度矩形板的自由振动，研究了此方法对求解自振频率的收敛性，得出了等厚度板前八阶固有频率和变厚度板的基频。Mukhtar[27]基于精细板理论，采用DTM和Talyor配置法分析了正交各向异性矩形板的自由振动，验证了DTM和Talyor配置法求解自振频率的结果一致。目前，用DTM分析变刚度弹性地基上受压非均质材料矩形板的振动和屈曲问题的研究，在国内外仍然鲜见有文献报道。

本工作假设弹性地基刚度系数、矩形板的弹性模量和密度沿板的长度方向呈指数变化，基于经典薄板理论，通过Hamilton原理建立变刚度Winkler地基上受压非均质矩形板自由振动与屈曲问题的控制微分方程并进行无量纲化，采用DTM再将无量纲控制微分方程及其边界条件变换为等价的代数方程，对变刚度Winkler地基上受压非均质矩形板的自由振动和屈曲特性展开研究。

1 控制微分方程及参数的无量纲化

考虑一各向同性非均质矩形薄板，建立如图1所示的笛卡尔坐标系。板的尺寸为a×b×h且受到垂直于y轴截面上的法向力Ny，将其放置在变刚度Winkler弹性地基上，这里k表示Winkler地基刚度系数。y=0和y=b处为简支边界(S)，其它两边边界条件则为简支(S)、固定(C)或自由(F)任意组合。下面在对矩形板四个直边的边界条件表示中，均按x=0、y=b、x=a和y=0处的次序给出。

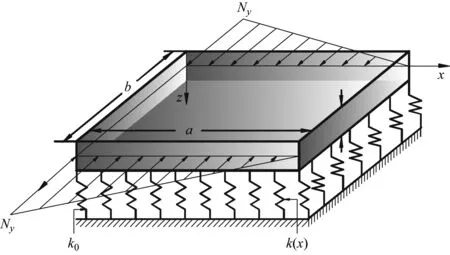
图1 变刚度Winkler弹性地基上受压非均质矩形板的几何

Fig.1 Geometry and coordinates of a compressed non-homogeneous rectangular plate resting on Winkler elastic foundation with variable stiffness

假设矩形板材料的弹性模量E、密度ρ和地基刚度系数k只沿x方向呈指数梯度变化，即

(1)

式中：E0、ρ0、k0分别为x=0处的弹性模量、密度和地基刚度系数；μ、β、α分别为弹性模量变化参数、密度变化参数和地基刚度变化参数。

这里仅考虑系统的横向位移而忽略纵向位移，由薄板振动理论，非均质矩形板横向运动时的应变能U、动能T和外力引起的势能V分别可表示如下

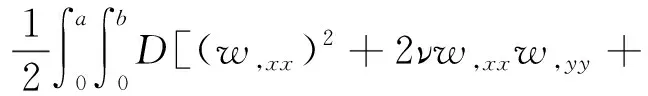
(w,yy)2+2(1-ν)(w,xy)2]dxdy

(2)

(3)

(4)

式中：D=Eh3/12(1-ν2)为板的弯曲刚度；ν为泊松比；Ny=-N0(1-γx/a)，N0为x=0处的压力强度；γ为载荷变化参数；w(x,y,t)为板的横向位移，t为时间。

Hamiltion原理表示如下

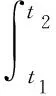
(5)

将式(2)～(4)代入式(5)，则变刚度Winkler地基上受压非均质矩形板横向运动的控制微分方程为

D(w,xxxx+2w,xxyy+w,yyyy)+2D,x(w,xxx+w,xyy)+

D,xx(w,xx+vw,yy)-Nyw,yy+kw+ρhw,tt=0

(6)

假设矩形板作简谐振动，横向位移w(x,y,t)可表示为

(7)

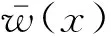
A0W″″+A1W‴+A2W″+A3W′+A4W=0

(8)

式中：

A0=1，A1=2μ，A2=μ2-2λ2，A3=-2μλ2，

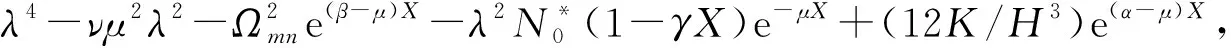
λ=mπa/b，K=a(1-ν2)k0/E0，

至于在X=0和X=1处的边界条件，其无量纲形式可分别表示如下

简支(S)：

(9)

固定(C)：

(10)

自由(F)：

(11)

2 控制微分方程及其边界条件的DTM变换

式(8)表示的变刚度Winkler地基上受压非均质矩形板横向自由振动的无量纲控制微分方程为变系数常微分方程，结合边界条件求其解析解较为困难，这里采用微分变换法(DTM)求解固有频率、振型以及屈曲临界载荷。DTM基于Taylor级数展开来求解微分方程，使用充分可微的多项式形式作为精确解的近似。经DTM变换，可将原微分方程(组)和系统边界条件转化为由离散函数构成的的代数方程(组)，非常适合计算机编程进行求解。对于原函数f(x)，根据函数的Taylor公式，经过DTM变换后的函数Fk定义为[10]

(12)

式(12)称为函数f(x)为x=x0时的微分变换的正变换式，Fk称为f(x)的微分变换形式。

设函数f(x)能展开为Talyor级数且收敛，则微分变换式可变换成原函数，其变换式为

(13)

式(13)称为微分变换的反变换形式。由式(12)和式(13)可得

(14)

由式(14)可知，微分变换法基于Talyor级数展开式，但DTM不需要进行函数各阶导数的求解。实际应用中，f(x)通过有限的级数表示，式(13)可改写为：

(15)

当X0=0时，式(8)由DTM变换为等价的代数方程形式如下：

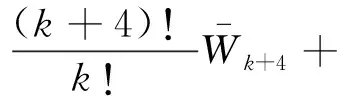
(16)

(17)

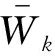
(λ2μ/12)c1+[(2λ2-μ2)/12]c2-(μ/2)c3，

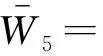
4λ2μ2-λ4+Ω2+λ2μ2ν)/120-

K/10H3]c1+[-(λ2μ+μ3)/30]c2-(μ/2)c3，

…，

(18)

这里，S0，S1，S2，S3是式(16)和(17)通过迭代r次而得到关于c0，c1，c2，c3的系数，c0，c1，c2，c3为待求的未知量。边界条件由DTM变换如下：

在X=0处，

简支(S)边界条件：

(19)

固定(C)边界条件：

(20)

自由(F)边界条件：

(21)

在X=1处，

简支(S)边界条件：

(22)

固定(C)边界条件：

(23)

自由(F)边界条件：

(24)

(25)

(26)

令无量纲固有频率Ωmn=0，给定参数可以求出各阶屈曲载荷Ncr。Ncr的求解过程类似于Ωmn的求解过程，同理可得

(27)

在对边简支对边固定(CSCS)、一边固定三边简支(CSSS)边界条件下，同理可求出含有未知量无量纲固有频率Ωmn以及屈曲载荷Ncr特征方程：

(28)

(29)

在FSSS、FSCS、FSFS边界条件下，同理可得：

(30)

(31)

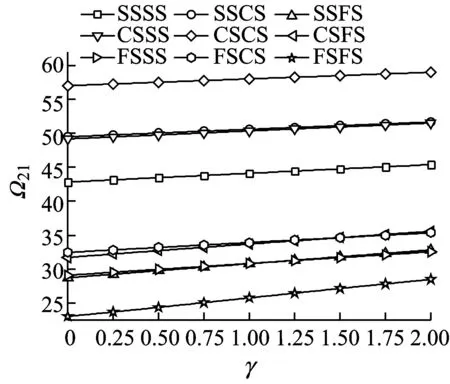
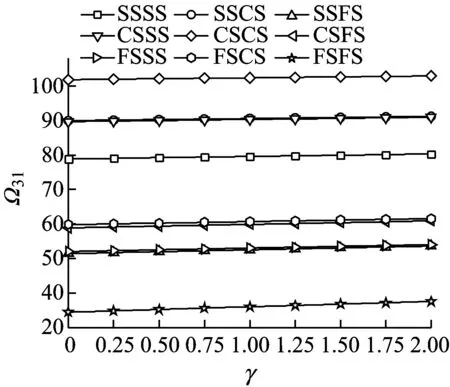
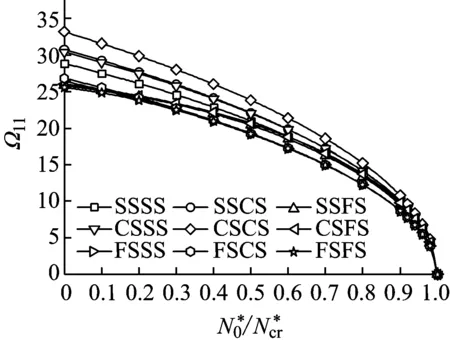
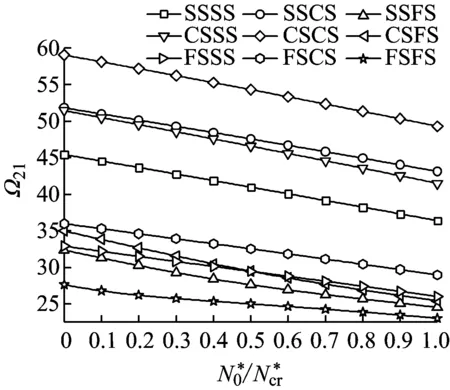
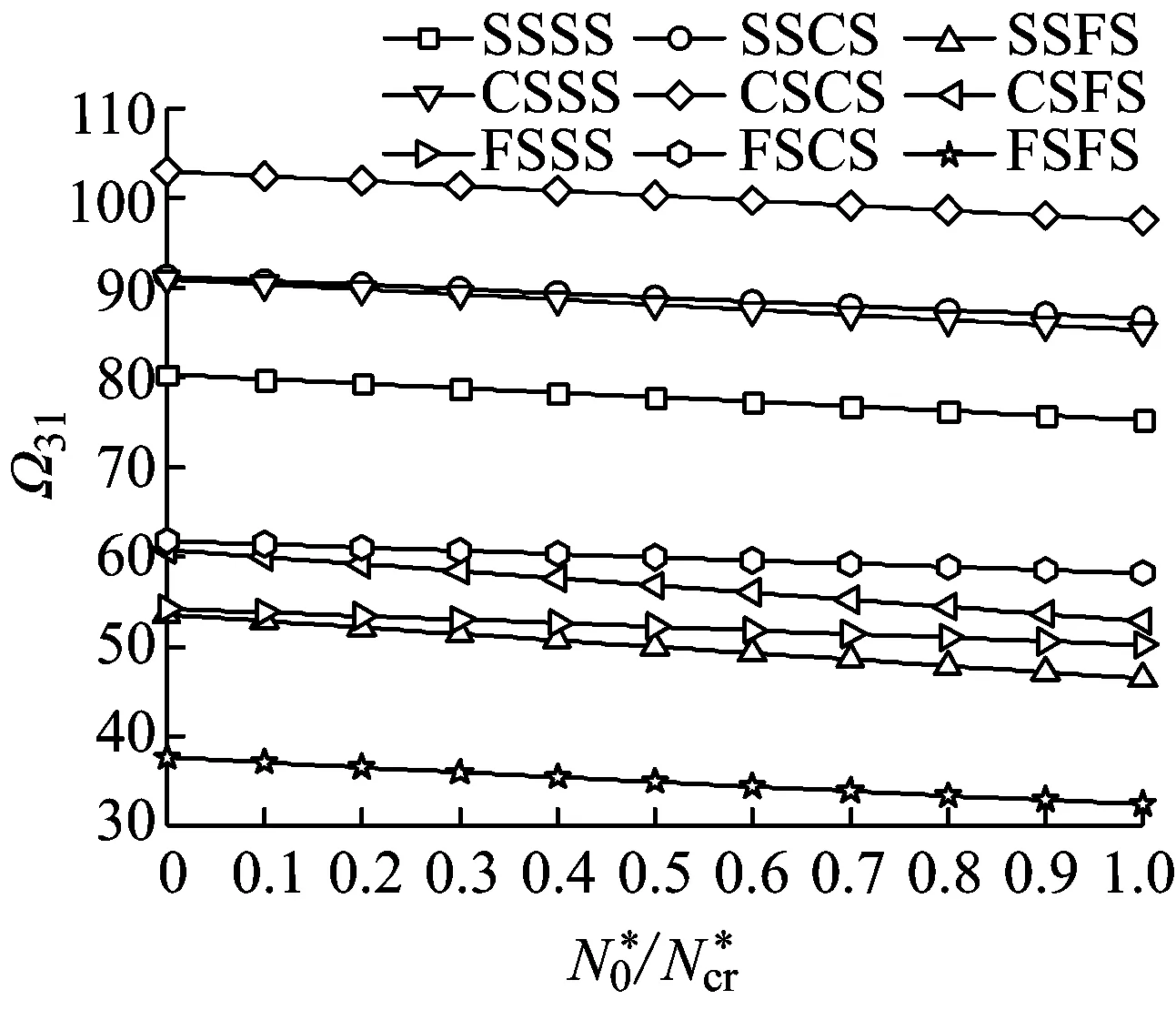
由式(26)～(31)，SSSS、SSCS、SSFS、CSSS、CSCS、CSFS、FSSS、FSCS、FSFS边界条件下的无量纲固有频率Ωmn和屈曲载荷Ncr可求出。为控制Ωmn和Ncr的精度，计算要求满足

(32)

式中：η1、η2为给定的迭代误差限，后面计算中均取η1=η2=0.000 001。

3 计算结果及分析

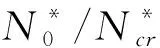
表1为a/b=1，K=0，N0=0，ν=0.3时SSSS边界条件下变刚度板前六阶无量纲固有频率Ωmn，并与何建璋等的辛弹性方法(精确解)进行对比，结果吻合。表1结果表明：采用DTM求解矩形板的自由振动与屈曲问题具有精度高、适用性强的特点。

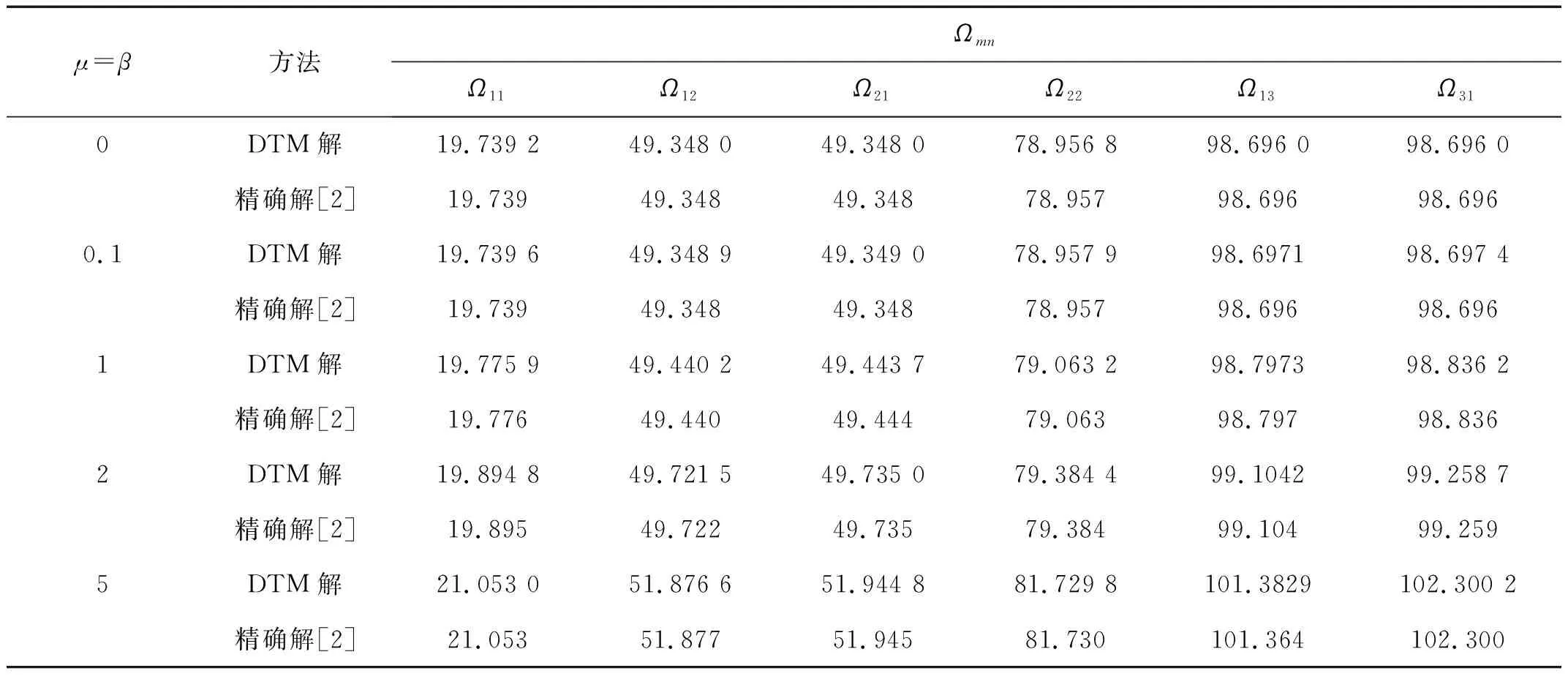
表1 SSSS边界条件下变刚度方板自振前六阶无量纲固有频率Ωmn

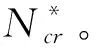
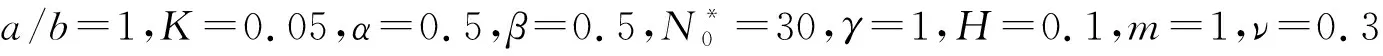
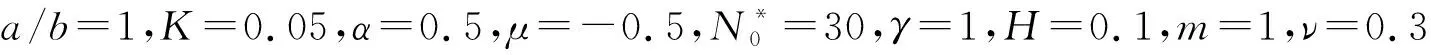
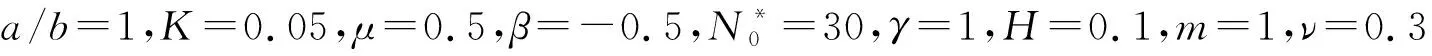
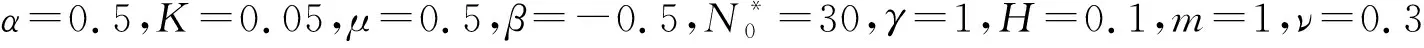
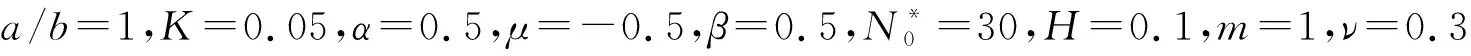
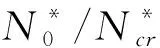
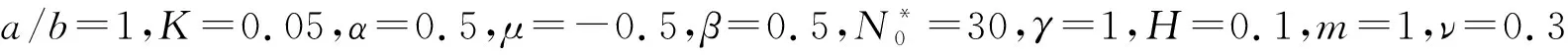
表2 不同边界条件下变刚度Winkler地基上受压非均质方板的无量纲屈曲临界载荷

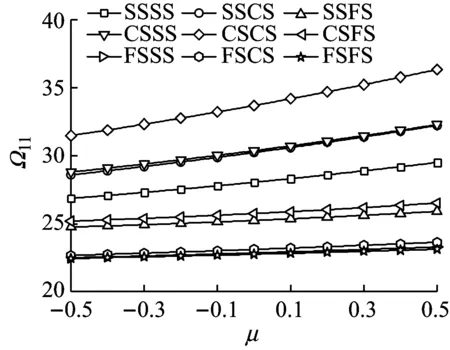
(a)

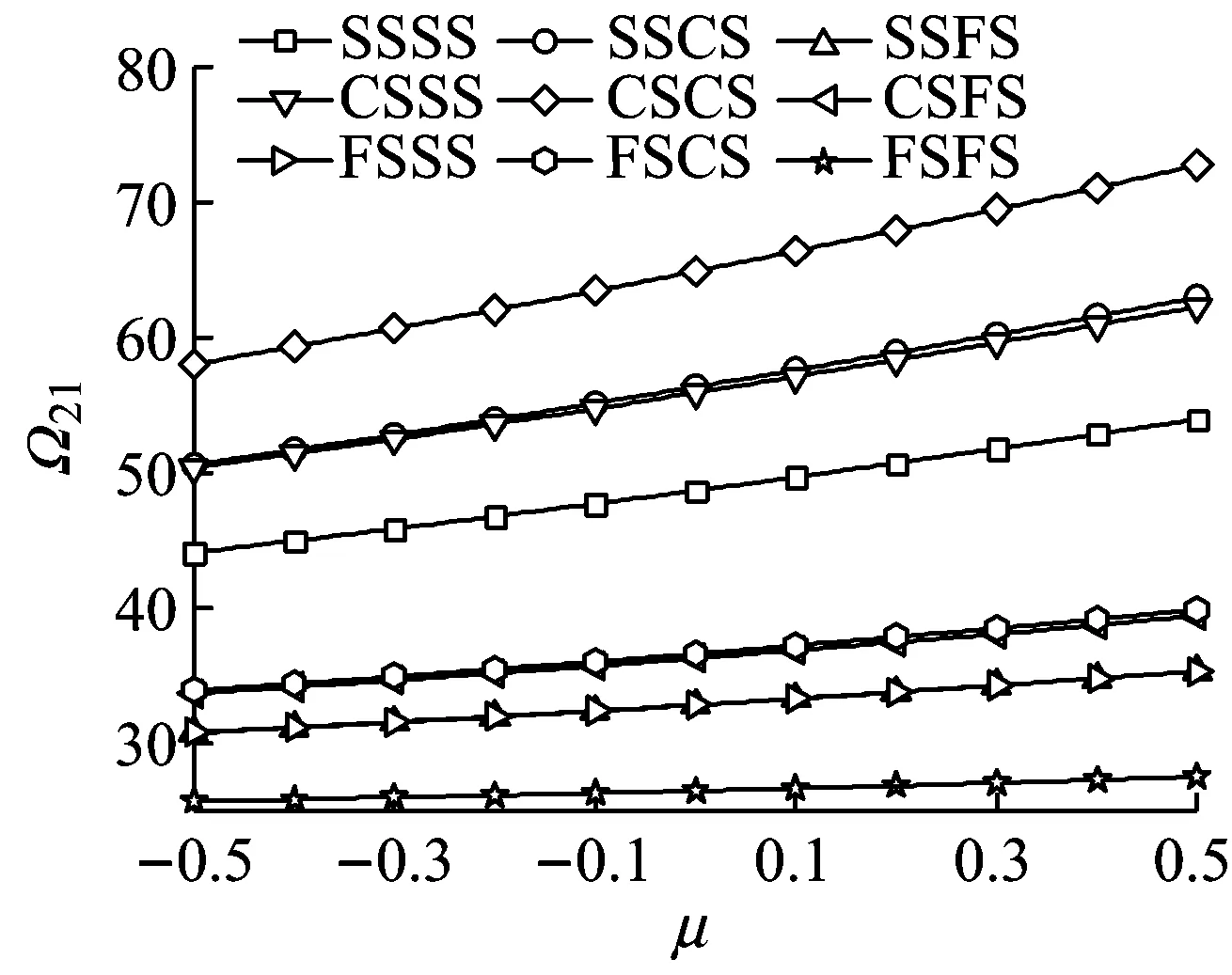
(b)

(c)

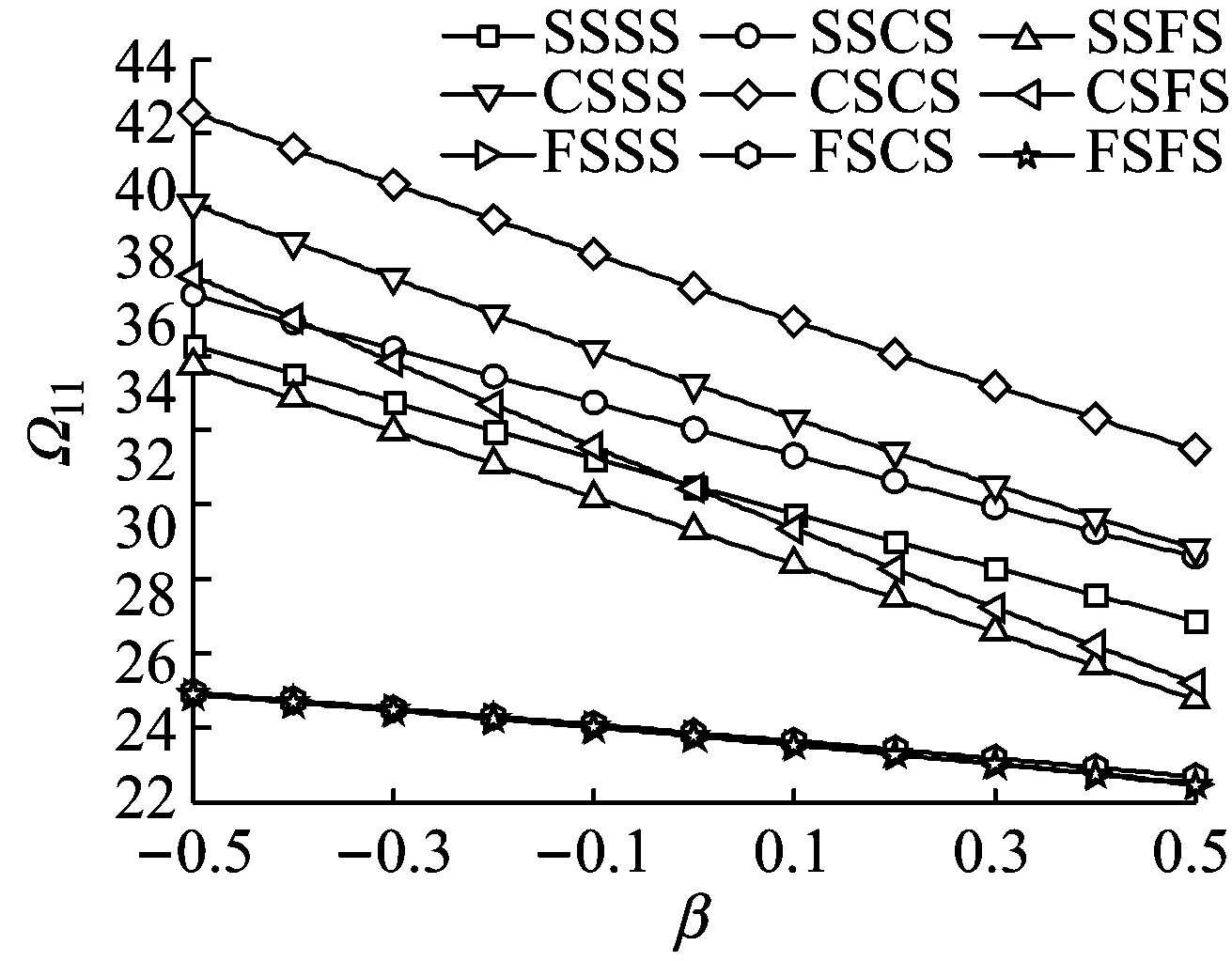
(a)

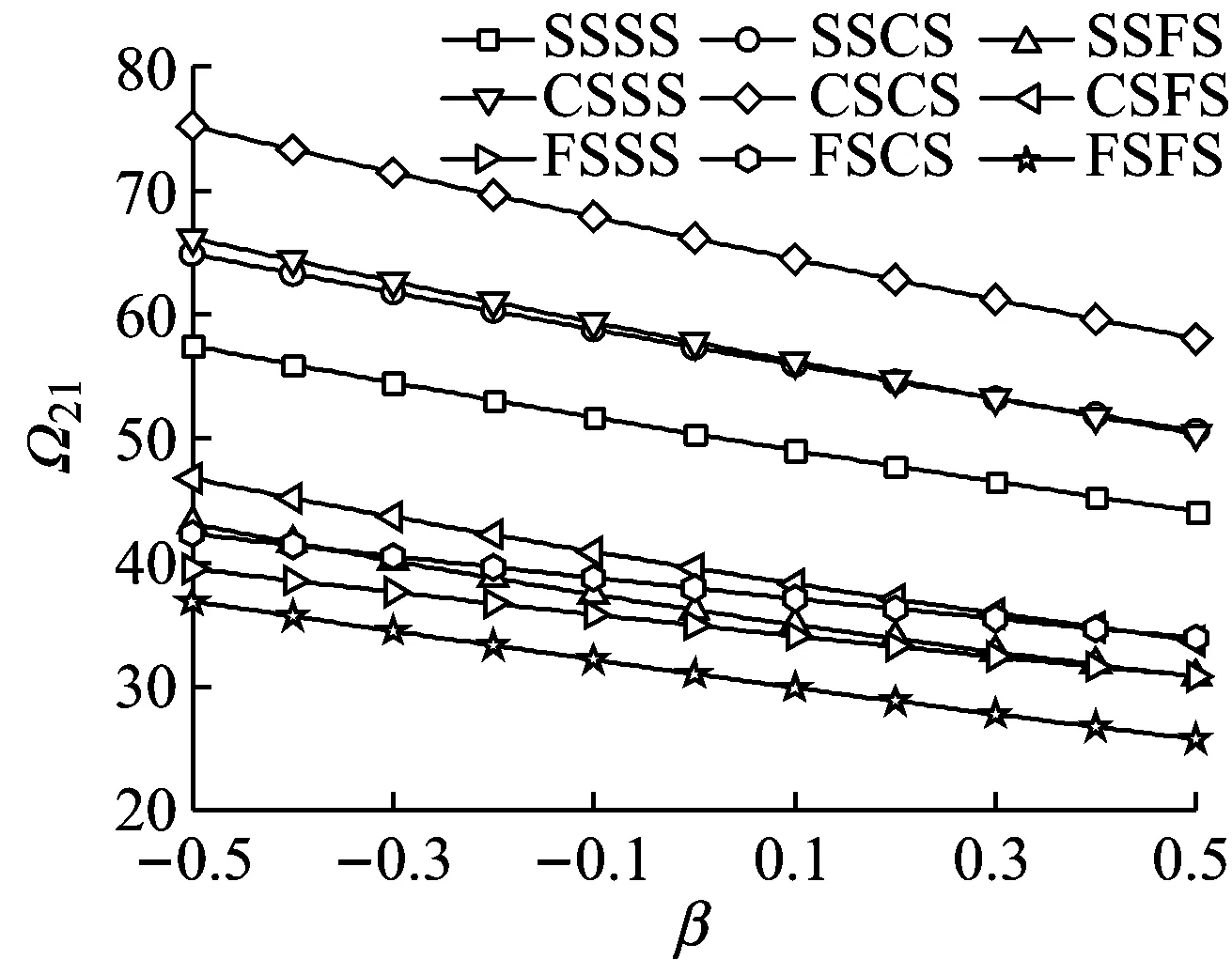
(b)

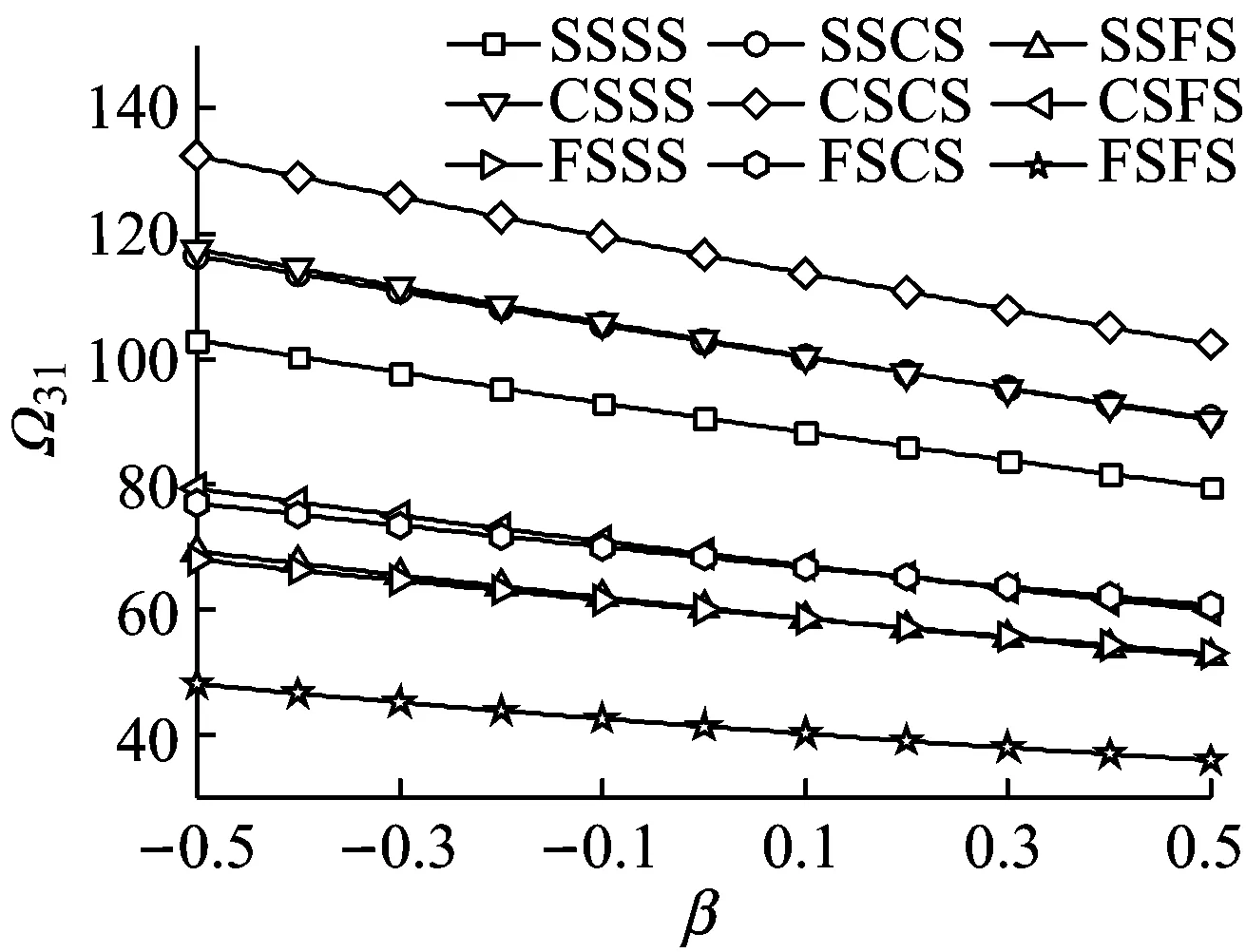
(c)

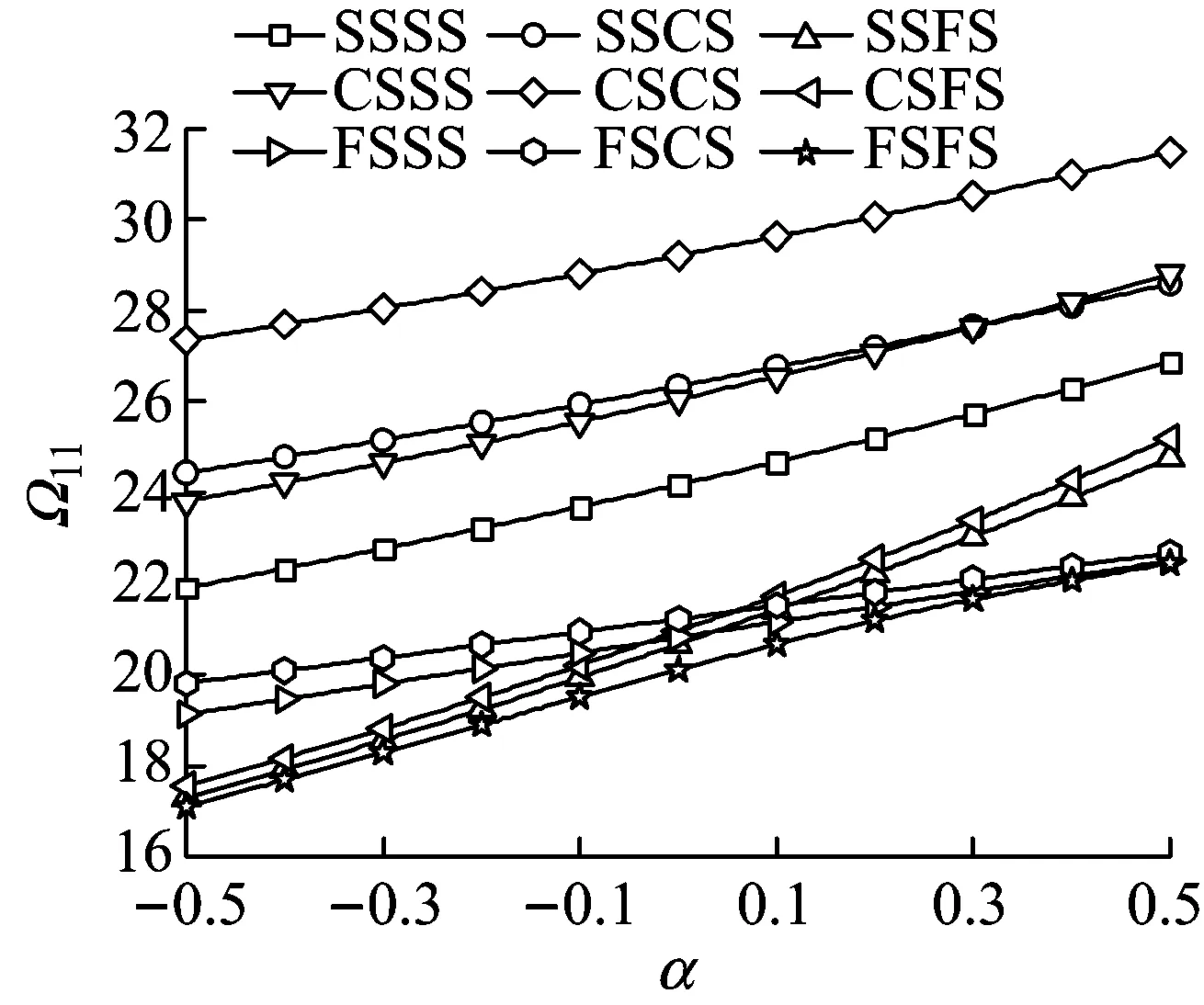
(a)

(b)

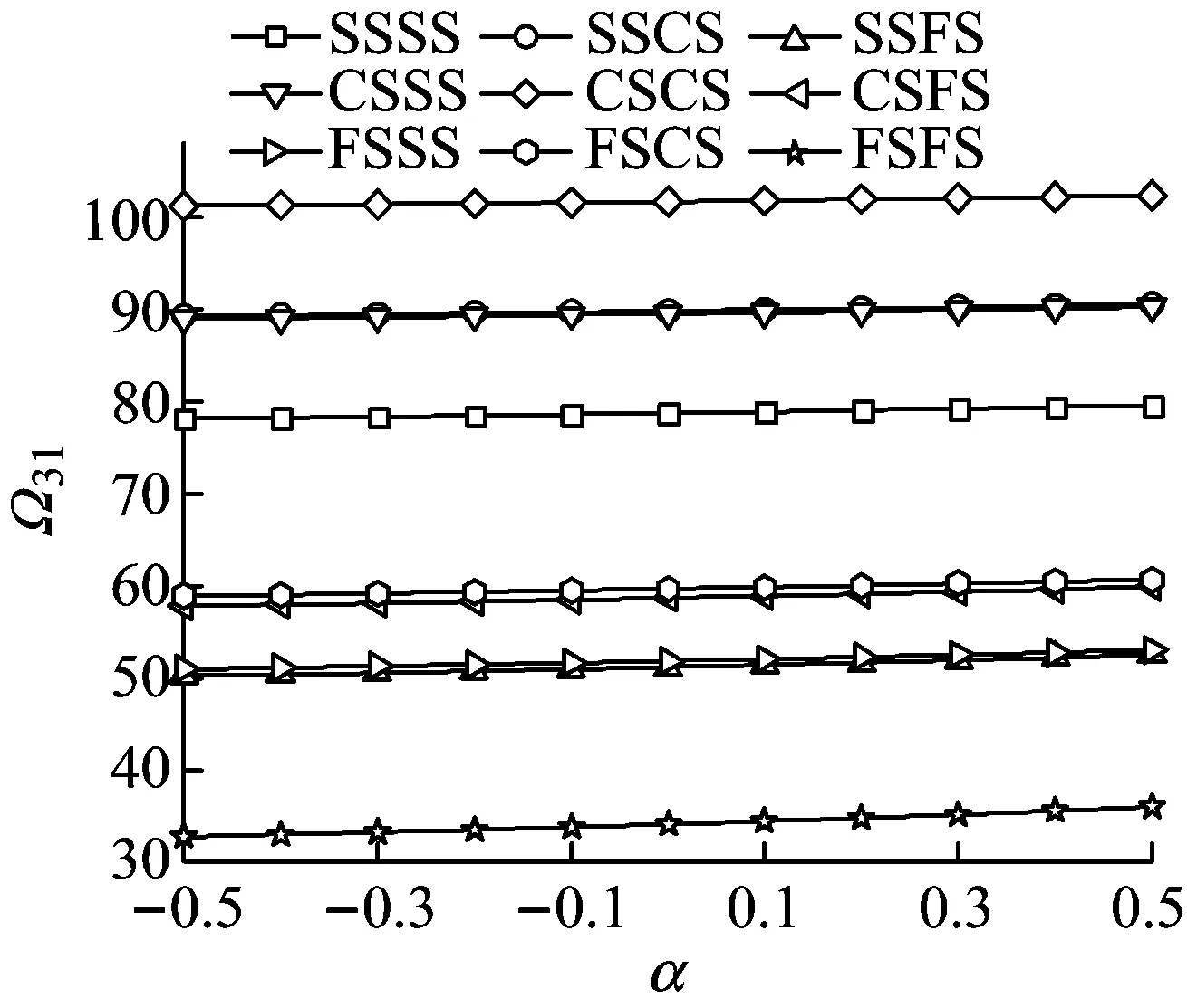
(c)

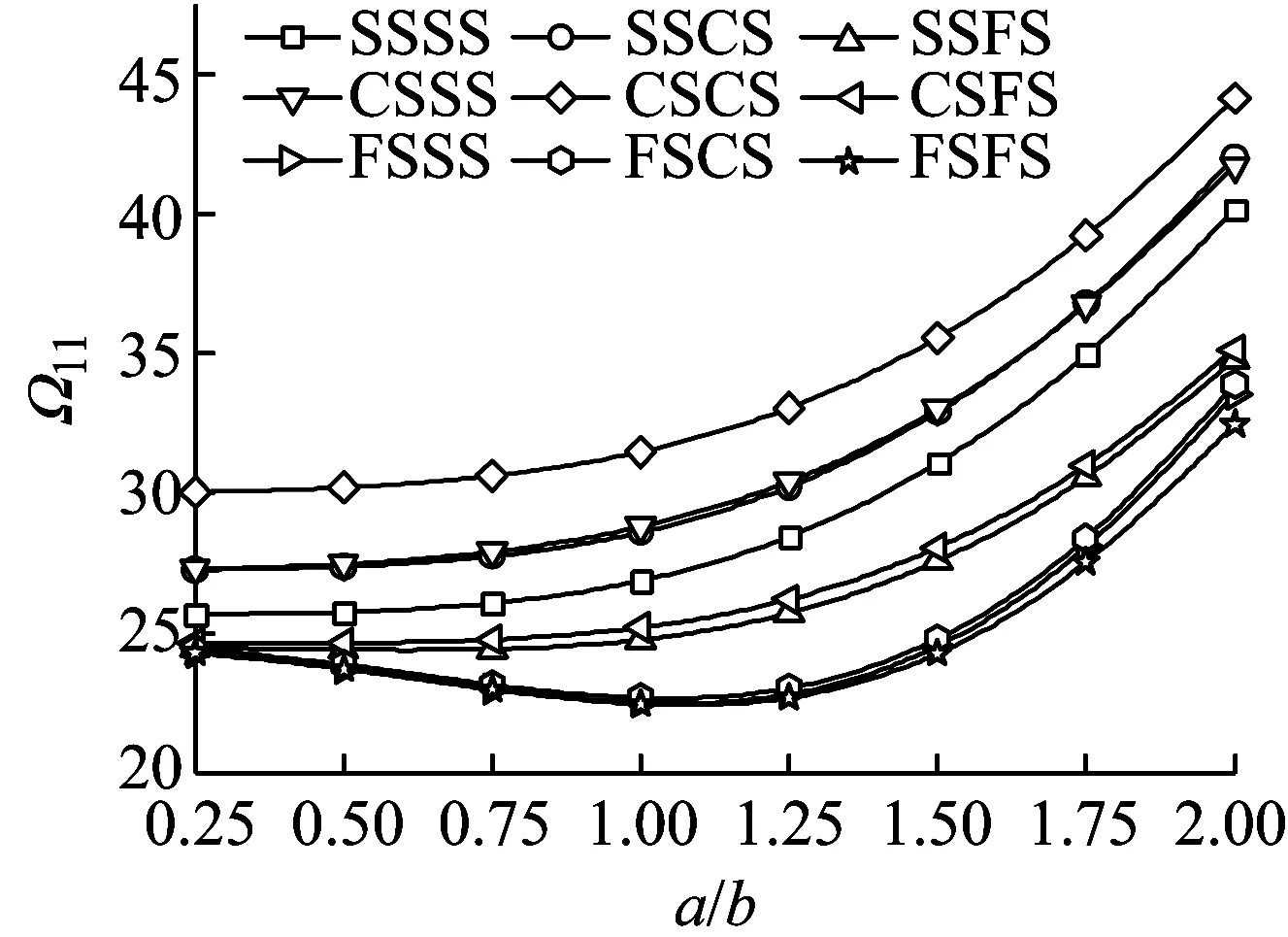
(a)

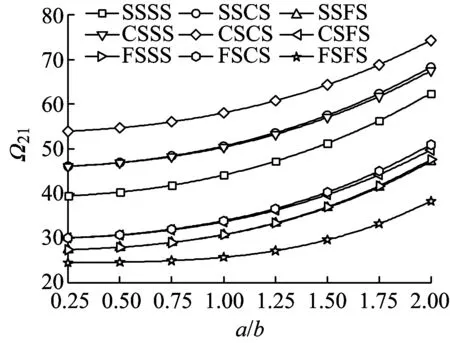
(b)

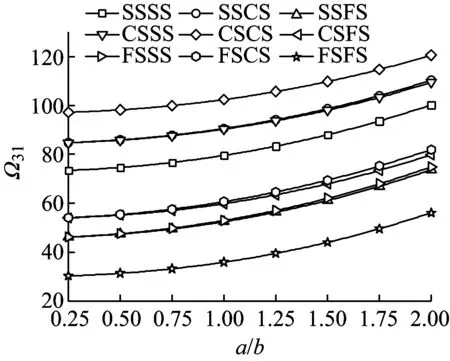
(c)

(a)

(b)

(c)

(a)

(b)

(c)

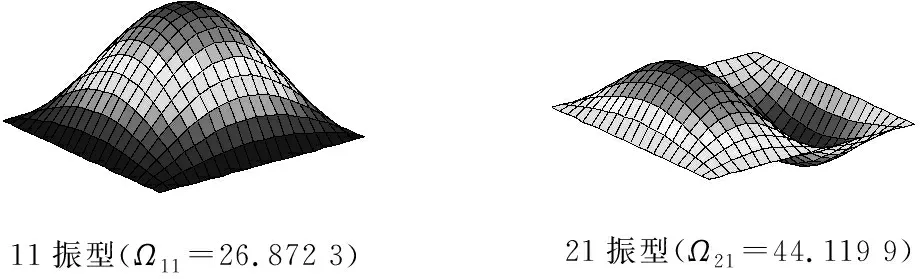
11振型(Ω11=26.872 3) 21振型(Ω21=44.119 9)

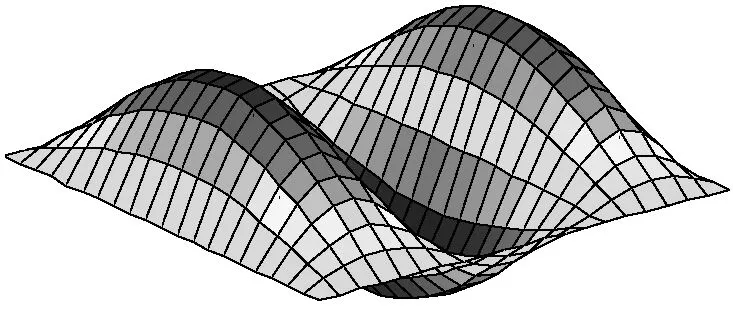
31振型(Ω31=79.575 8)

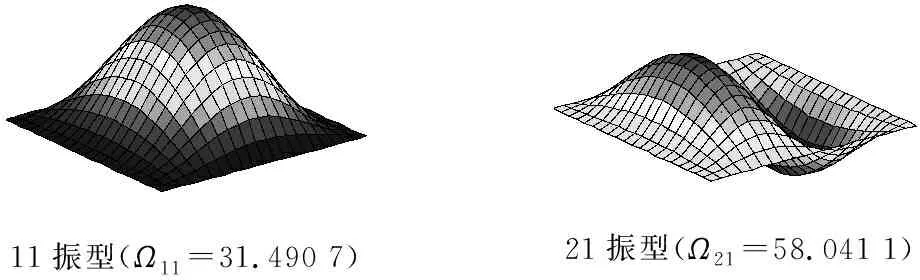
11振型(Ω11=31.490 7) 21振型(Ω21=58.041 1)

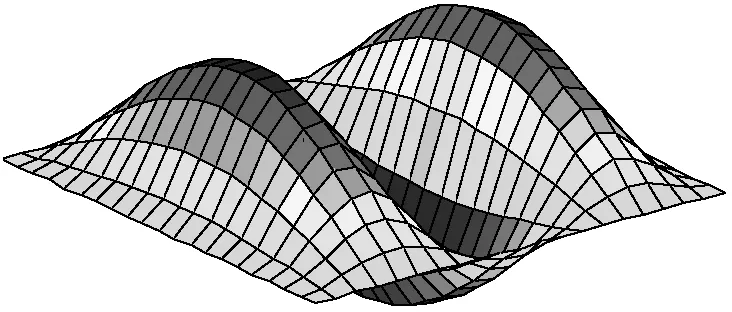
31振型(Ω31=35.972 2)

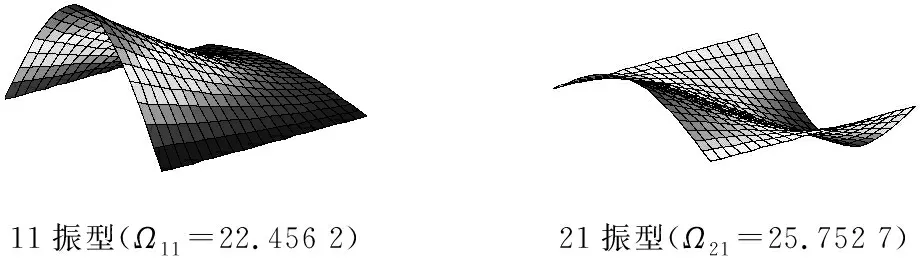
11振型(Ω11=22.456 2)21振型(Ω21=25.752 7)

31振型(Ω31=35.972 2)

Fig.8 The first three modes for compressed non-homogeneous rectangular plates resting on Winkler foundations with variable stiffness for SSSS, CSCS and FSFS boundary conditions

4 结 论

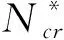
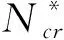
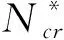
(4) 本文采用DTM求解变刚度Winkler地基上受压非均质矩形板的自由振动与屈曲问题原理简单，易于编程，具有较高的计算精度，从而为求解此类问题提供了一种可供选择的简便有效方法。