基于UKF的结构动荷载识别方法与试验验证

郭丽娜， 宋开明， 张延哲， 丁 勇,3

(1.东北农业大学 水利与土木工程学院，哈尔滨 150030；2.哈尔滨工业大学 土木工程学院，哈尔滨 150090；3.中电建冀交高速公路投资发展有限公司，石家庄 050000)

结构动力学问题可分为两大类：若已知结构外界输入，需要通过结构试验或数值仿真分析研究结构响应和性能，此类问题称为正问题；若已知结构响应，需估计结构外荷载、识别结构参数，此类问题统称为反问题[1]。动力荷载对结构的破坏常为静力荷载破坏作用的2倍～4倍。结构外荷载常随时间变化且具有复杂的随机性，这使得实际工程结构动力荷载的识别问题成为工程界亟待解决的问题之一。

通过直接测量和系统识别方法评估两种方法均可获得外荷载时程，但在实际工程中，直接测量的方法常受到测点数目和测点位置的限制难以应用。因此，通过系统识别的方法进行结构外荷载识别显得尤为重要。

目前，国内外学者已经提出多种线性或非线性结构参数识别的系统识别方法，如最小二乘算法[2]、卡尔曼滤波器算法[3-4]、蒙特卡洛算法[5-7]、以及以损伤因子为目标函数的荷载识别方法[8]。卡尔曼滤波器算法是一种有效识别线性结构参数的均值方法，对于线性结构有着较好的估计效果。为了克服其只能应用于线性结构系统的缺点，衍生出了等效线性化的近似方法，从而发展出可用于非线性系统识别的扩展卡尔曼滤波算法。而后为了改善卡尔曼滤波算法对非线性系统的识别精度，又发展了无迹卡尔曼滤波算法等方法，该方法避免了非线性函数线性化所带来的误差且不用计算复杂的雅可比矩阵，具有操作简单、滤波精度高及易收敛等优点。基于切比雪夫标准正交多项式分解的结构系统荷载识别和参数识别方法已得到众多学者研究与验证[9-10]，在实际运用中具有一定可行性。当前，已有一部分学者通过数值仿真分析验证了UKF对结构体系几何非线性、材料非线性的适用性[11]。

本文利用基于UKF算法的直接荷载识别法对作用于地震模拟振动台的外部激励进行识别，并针对出现漂移现象的荷载识别结果提出了位移-加速度联合观测值和噪声水平自适应评估两种解决方法，改善了识别过程的收敛性，验证了所提方法的合理性和有效性。

1 UKF算法流程

假定非线性离散时间系统的状态方程与观测方程满足以下形式：

xk=f(xk-1,uk-1,k-1)+vk-1

(1)

yk=h(xk,uk,k)+wk

(2)

式中:k∈R为离散时间，xk∈Rn为n维的随机状态向量，yk∈Rm为m维观测向量。假设非线性状态方程f(·)和非线性观测方程h(·)在状态量xk处连续并且可微。vk～N(0,Qk)是过程噪声，满足高斯分布，wk～N(0,Rk)为观测噪声，同样满足高斯分布。

无迹卡尔曼滤波器算法的递推过程如下：

(1) 预测步：构造2n+1个sigma点，准则如下：

(3)

(4)

(5)

(6)

其中：

(7)

(8)

(9)

(10)

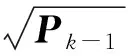
(2) 更新步：利用UT变换和观测量可以计算得到下一步状态量的均值与方差：

(11)

(12)

(13)

(14)

(15)

计算卡尔曼增益并更新状态量均值与方差得：

(16)

(17)

(18)

式中：yk表示第k步的观测值。

通过上述步骤的循环递推运算，可以发现UKF算法不需要对非线性函数进行线性变换，避免了复杂的雅克比矩阵的运算。

2 荷载识别方法

2.1 间接荷载识别法

由于外部荷载的不确定性及其幅值的时变性，很难在状态空间内使用确定性的模型来表征外部荷载。考虑到荷载时程是一个随机过程，即可以通过正交分解的办法将荷载时程分解成一系列系数和多项式正交基乘积的线性组合形式，并且这些系数之间是相互独立的。这种分解方法可以对随机过程进行有效的量化拟合，方便建立数学模型进行数学分析。

在分解荷载时程的过程中，发现基于标准正交基的随机过程分解方法效果很好[12-13]，同时还可以避免求解复杂的Fredholm积分方程。研究发现，切比雪夫(Chebyshev)分解方法是适用于随机输入正交分解的较准确的分解方法[14-15]。切比雪夫正交多项分解如下所示：

(19)

式中:Linp是输入长度，Nm是分解阶数，基于切比雪夫标准多项式分解，结构运动方程可以写作：

(20)

即基于荷载正交分解的荷载识别UKF算法的状态空间方程可以写作如下：

(21)

式中:状态变量k和c的作用是识别结构系统的刚度和阻尼，如果不需要进行识别，可以移除，即只留下正交展开系数w。

2.2 直接荷载识别法

由于间接荷载识别法需要识别的参数很多，并且识别出来的只是正交展开系数，还需多一步系数与正交基的乘积求和才能得到待识别荷载，除此之外项数的选取也是一个问题，很难统一定论，所以为了减少待识别的参数个数以及简化运算过程，可以将待识别的外部荷载直接作为状态变量进行识别，即直接荷载识别法。

假设有线性离散系统如下：

xk+1=Axk+Bpk+wk

(22)

式中:A和B是系统矩阵，wk(wk∈Rns，0≤k≤∞)是随机过程噪声，ns是状态量个数。

为了补充式(22)，假设在时间k以及k+1处有一个荷载矢量p∈Rnp：

pk+1=pk+ηk

(23)

式中:ηk是随机过程成分，ηk∈Rnp，0≤k≤∞。通过合理选择过程噪声ηk的协方差矩阵，利用式(23)可以估计荷载时程。

通过结合式(22)和(23)，并且重新定义状态量xa(上标a代表扩展)得：

(24)

由此，扩展后的状态方程为：

(25)

矩阵Aa定义为：

(26)

噪声矢量ζk∈Rns+np取决于模型误差wk∈Rns以及荷载随机增量ηk∈Rnp：

(27)

含有未知噪声矢量vk的经典离散时间观测方程由于扩展状态量变为：

(28)

式中:d∈Rnd,代表测量数据矢量；矩阵Ga∈Rnd×(ns+np)是由输出影响矩阵G和直接转换矩阵J组合而成的：

(29)

于是，扩展状态量的状态方程和观测方程表达式为

(30)

式中:用于识别的系统矩阵A、B、G和J可以根据不同方法获得。

3 仿真算例

3.1 单自由度滞回非线性剪切模型

本部分所用模型为单自由度滞回非线性模型，如图1所示，非线性成分采用Bouc-Wen模型模拟，在只考虑结构单方向运动时，其运动方程可表示为：

(31)

式中，RT(x,z,t)=αkx+(1-α)kz(t)，并有

(32)

式中:z为滞回位移成分;m,c和k分别为结构系统的质量、阻尼和刚度;α为系数，用来描述结构滞回特性与弹性程度的比值，取值范围[0 1]。当α取1时，表示屈服后刚度与屈服前刚度相等，即结构为纯弹性；当α取0时，表示系统总是处于屈服的状态，即此时认为系统是纯滞回性的。在此算例中取α=0，即：

(33)

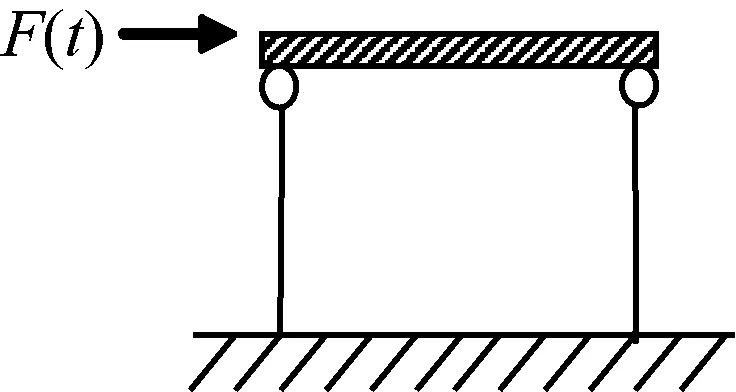
图1 单自由度结构模型

3.2 仿真结果

采用的模型参数取值为：m=0.1 t、c=0.32 kN/(m/s)和k=38 kN/m，非线性参数取值为：β=4、γ=4和n=2，外部荷载作用在该单自由度质量上。其中外荷载考虑了两种情况，分别为F(t)=A×sin(4×π×t)kN的周期荷载以及冲击荷载。其中A为在一定范围内线性变化的常数，用来模拟时变荷载，假定荷载的作用时长是3 s，时间步长为0.001 s。

模拟过程中采用的噪声为百分比噪声，施加原则如下：

(34)

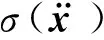
本算例正问题采用四阶龙格库塔求解，对于非线性结构系统，通过状态空间方程的形式可以将二阶结构运动微分方程转换为一阶运动微分方程，即：

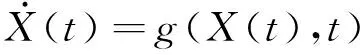
(35)

当采用直接荷载识别法时，取状态量为：

(36)

当采用间接荷载识别法时，取状态量为：

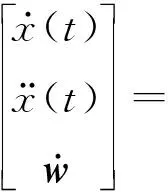
(37)

通过数值模拟，我们得到仿真结果,如图2和图3所示。

图2和图3分别表示无噪声和5%噪声时，周期荷载作用下，两种识别方法的识别结果。采用范数相对误差对识别精度加以考虑：

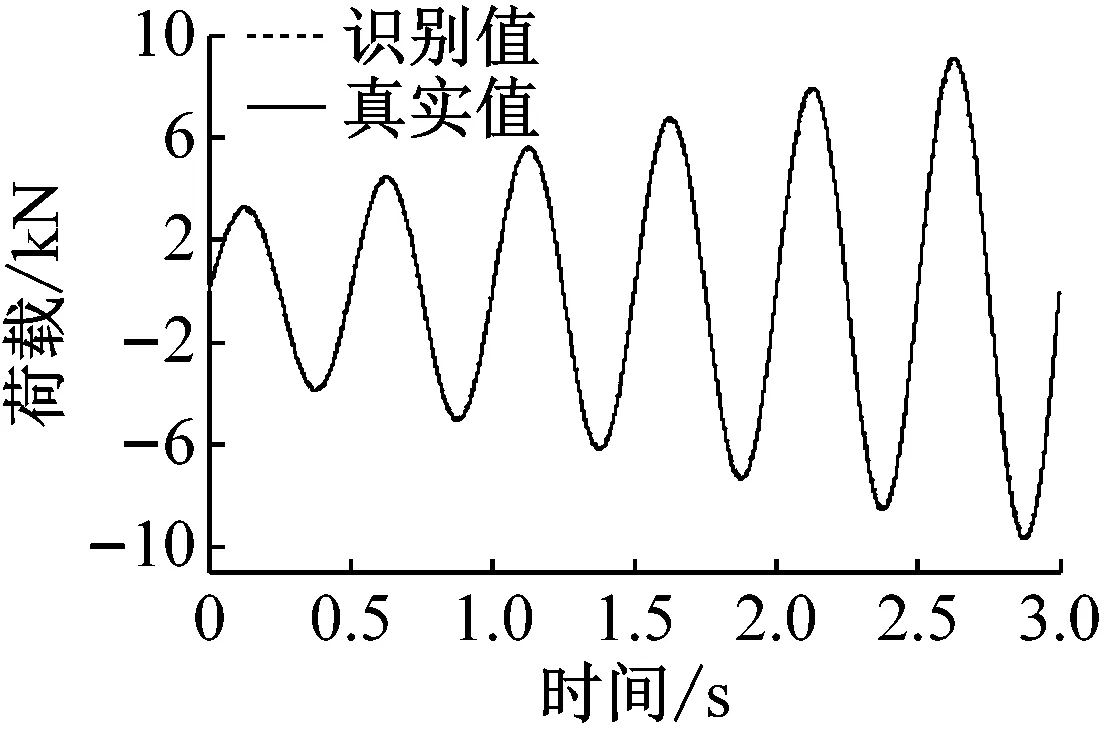
(a) 直接荷载识别法-无噪声

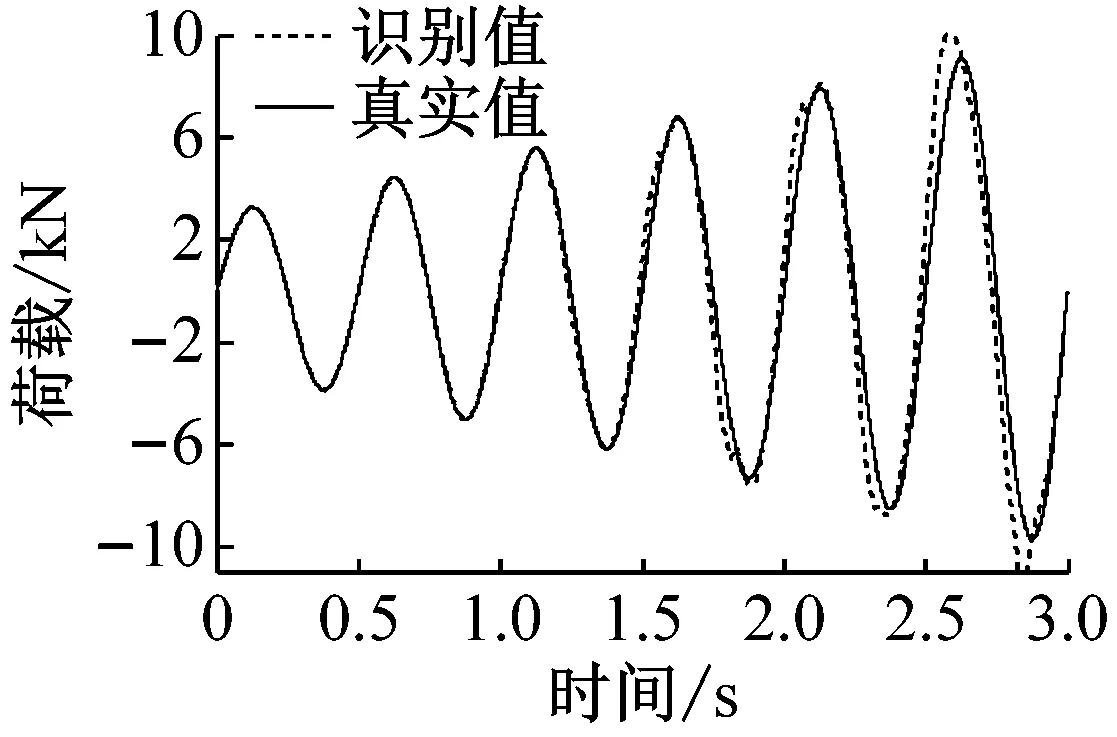
(b) 间接荷载识别法-无噪声-15阶

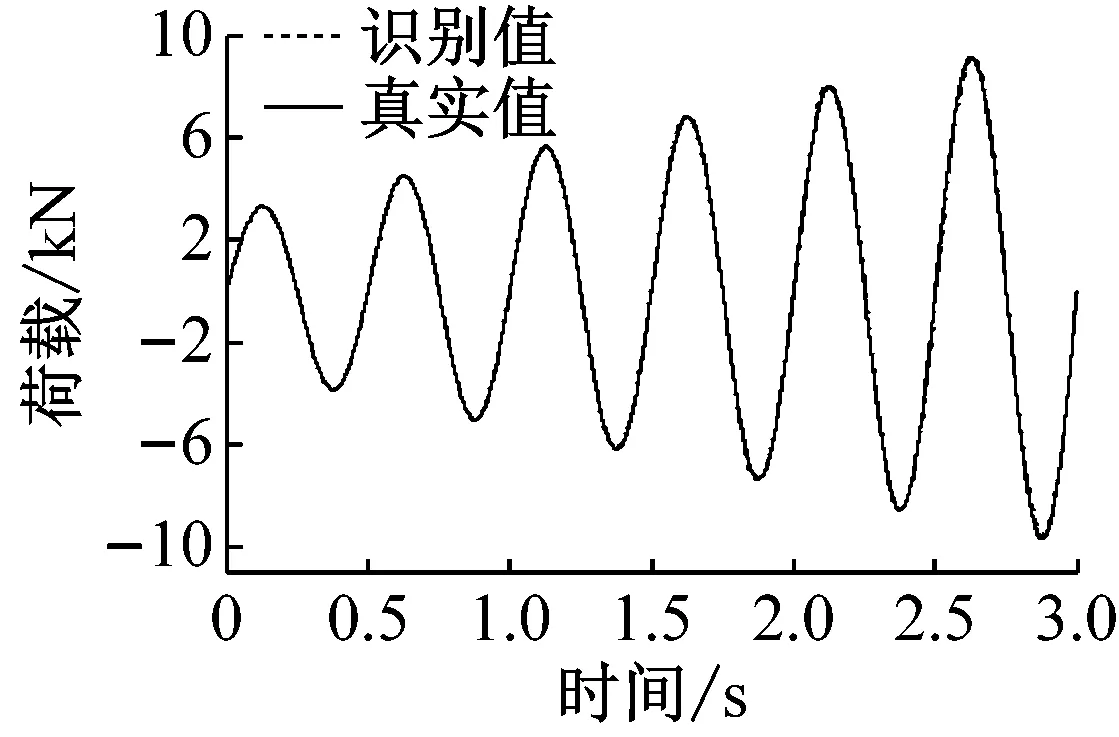
(c) 间接荷载识别法-无噪声-20阶

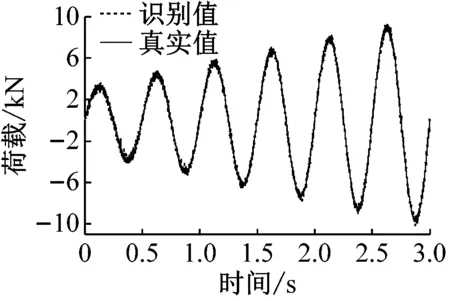
(a) 直接荷载识别法-5%噪声

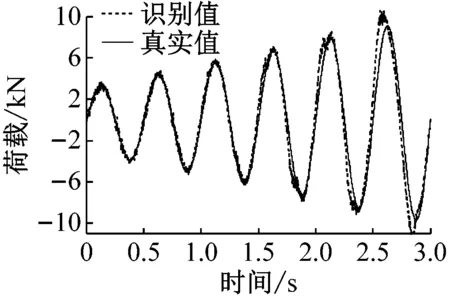
(b) 间接荷载识别法-5%噪声-15阶

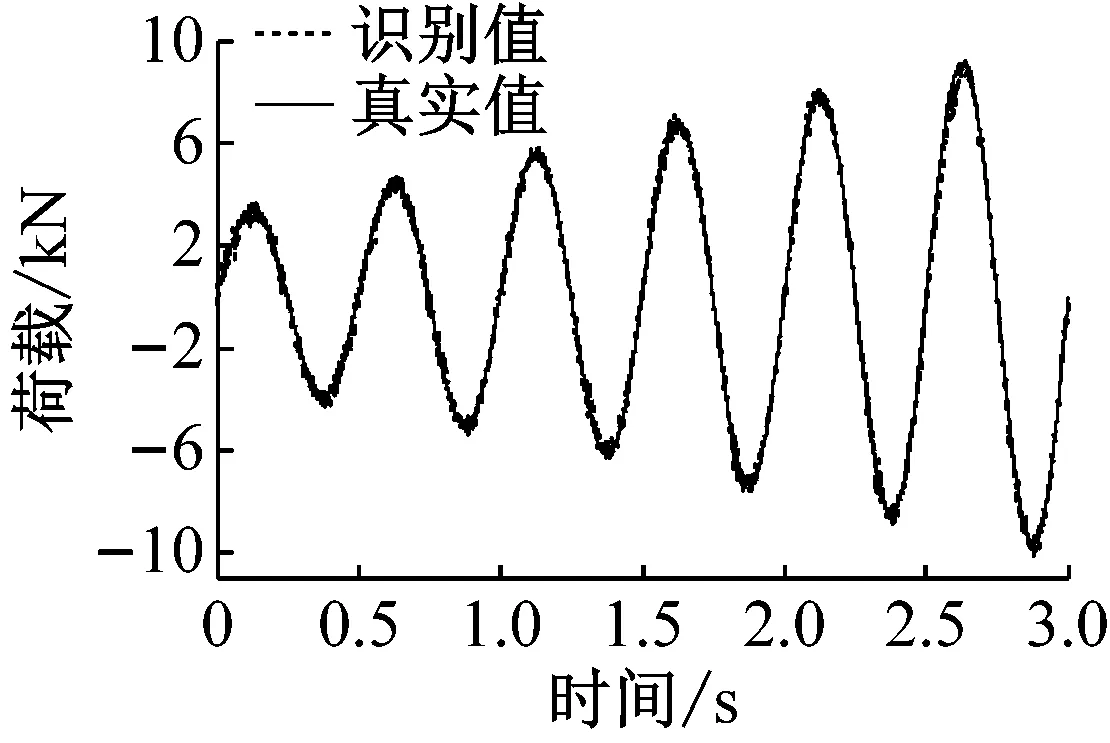
(c) 间接荷载识别法-5%噪声-20阶

(38)

图4和图5给出了冲击荷载作用下，两种识别方法的对比情况，并考虑了噪声的影响。

对于上述分析结果，将求得的直接荷载识别法与间接荷载识别法的范数相对误差,见表1和表2。

从图分析结果可以看出，间接荷载识别法精度受正交多项式分解阶数的影响较为明显，一般情况下，当正交分解阶数增大时，间接荷载识别法的精度会显著提高，与此同时，外荷载矩阵及协方差矩阵也随之增大，因此计算效率有所降低，由此可见，对间接荷载识别法，确定恰当的正交分解阶数是协调识别精度和计算效率的重要环节。直接荷载识别法，计算效率较高，抗干扰能力强，但识别精度不容易控制。综上，直接荷载识别法应用于单自由度非线性模型荷载识别的合理性和有效性得以验证。

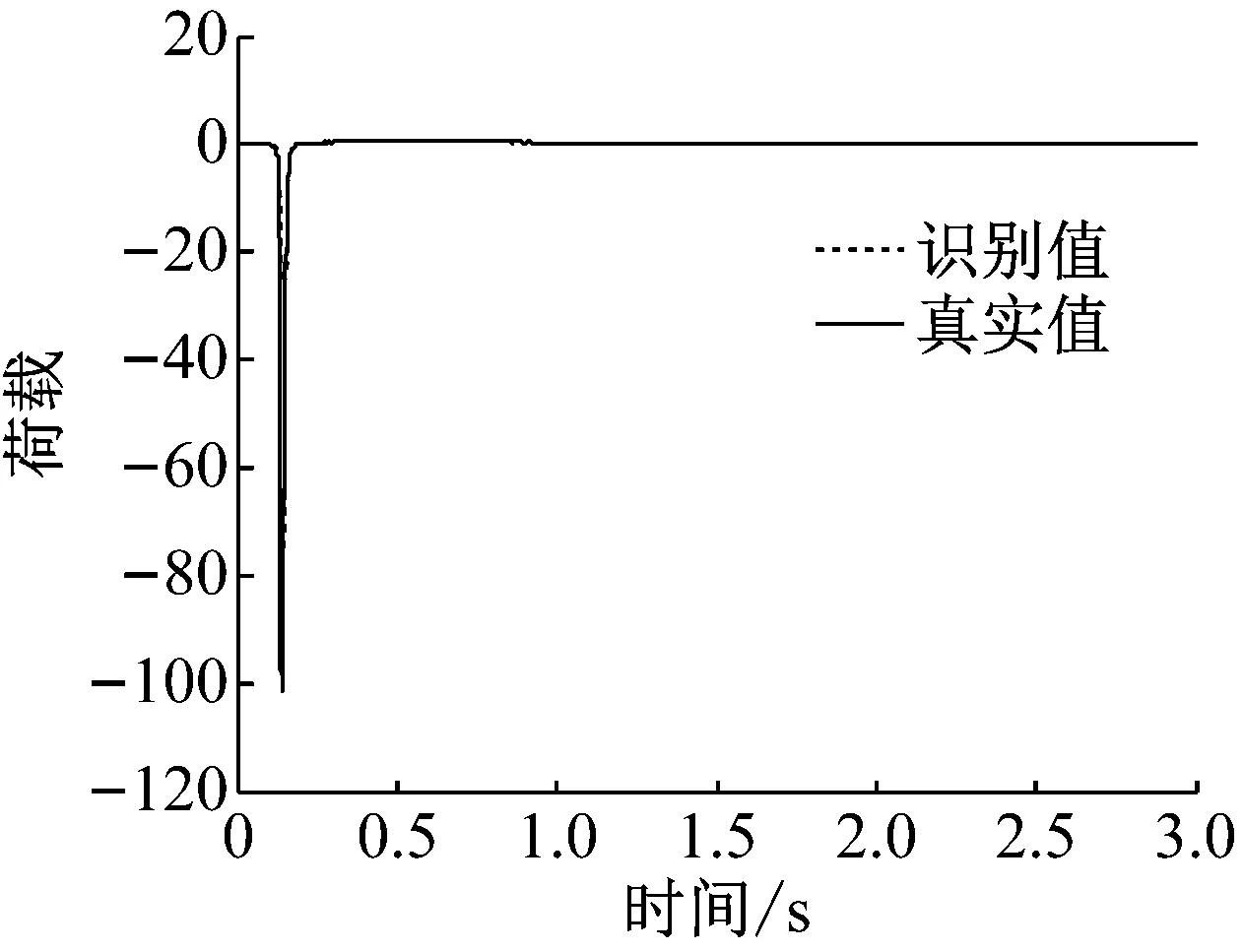
(a) 直接荷载识别法-无噪声

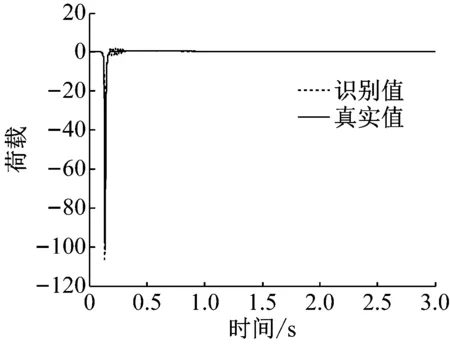
(b) 间接荷载识别法-无噪声-40阶

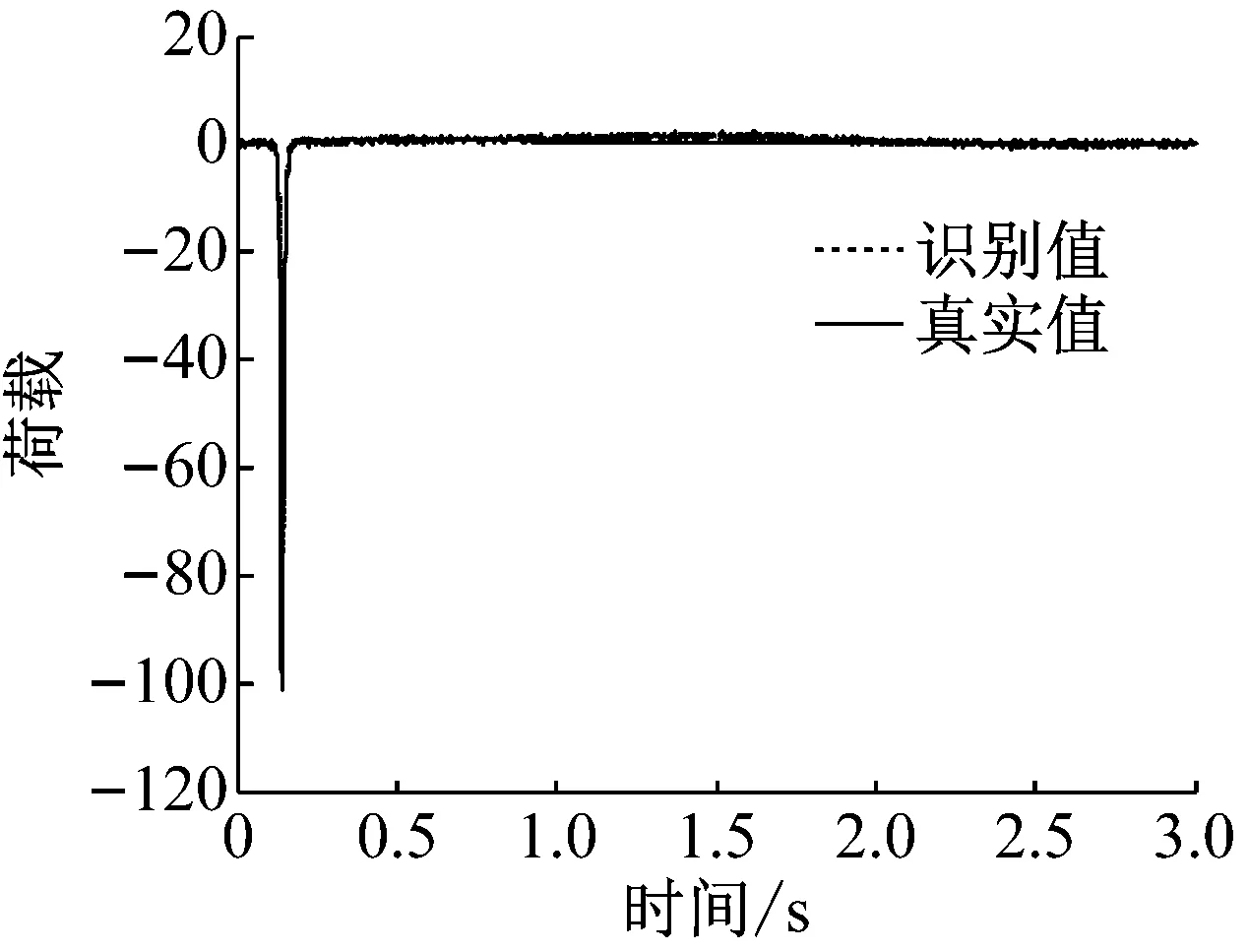
(a) 直接荷载识别法-5%噪声

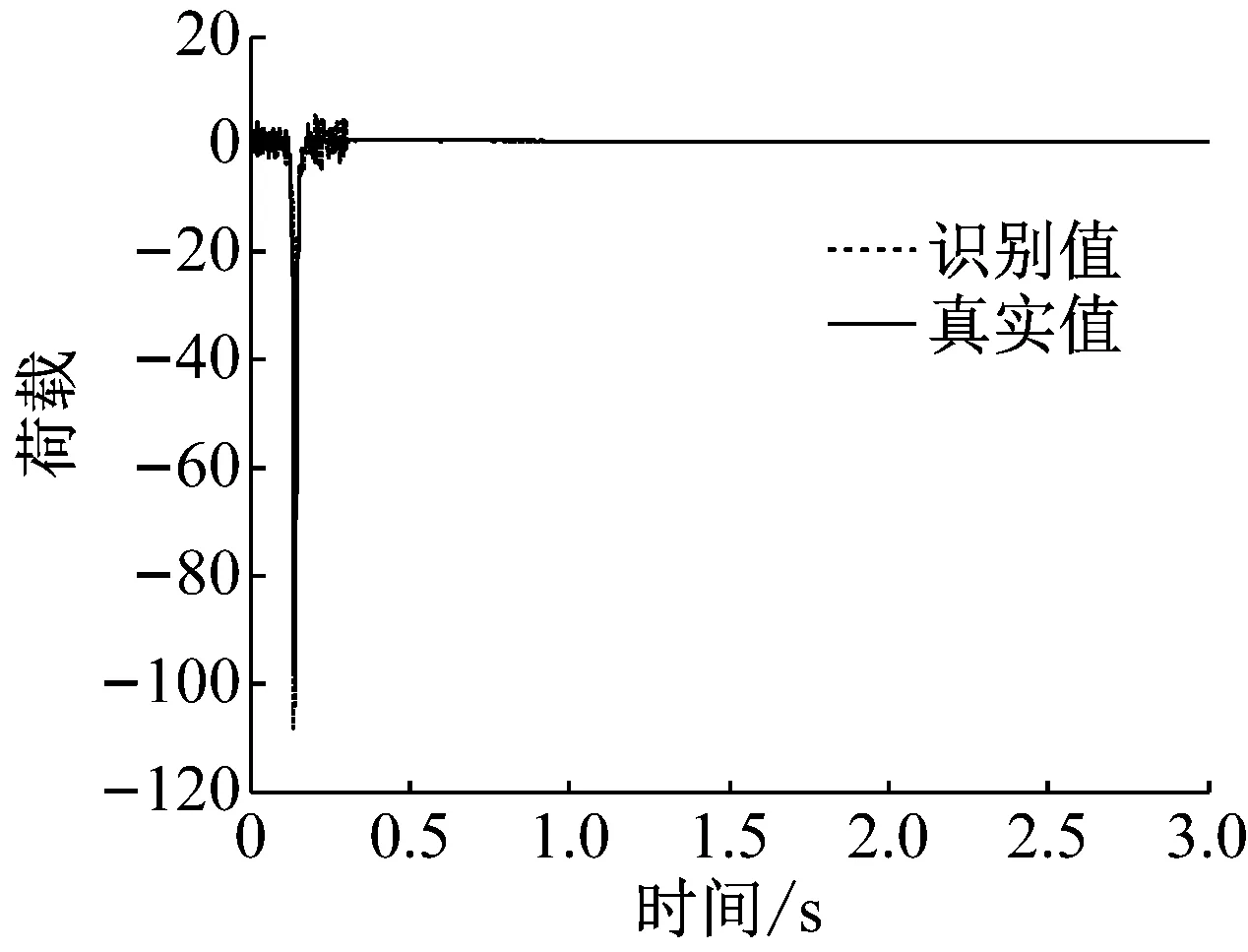
(b) 间接荷载识别法-5%噪声-40阶

周期荷载冲击荷载间接识别法直接识别法间接识别法直接识别法正交分解阶数1520———3040———范数相对误差/%22.832.271.2414.869.7213.43%

表2 5%噪声时范数相对误差

4 基于无线传感的振动台荷载识别试验验证

4.1 无线传感系统

本研究所使用的无线传感系统为所在团队自主集成研发。其中，传感器节点有各自的物理IP，通过自身配置的WiFi模块与无线路由器连接，PC机通过网线或者WiFi连接到路由器上，测试数据由传感器节点通过WiFi在线传输给PC机。传感器能量供应方式有两种：外电源连接和电池连接。无线传感系统工作原理示意图,如图6所示。

传感器节点主要由加速度传感器芯片、ARM处理器和WiFi模块组成，如图7所示。本系统最大采样精度12bits，有三种量程±2 G、±4 G、±8 G，可根据应用场合选择，最大采样频率800 Hz。该传感器具有封装小、功耗低、安装方便等特点。ARM处理器选用主频72 MHz，片内集成20 KRAM和64K FLASH，以及多达20个GPIO，适合用于低成本、低功耗的嵌入式领域。WiFi模块选用业界成熟的simple WiFi，支持802.11b/g标准，支持AP和STA模式，配置简单，安全性高。电源选择简单、安装方便，集成模块示意图如图8所示。为了保证数据传输的可靠性，传感器节点和PC之间使用自定义的协议进行通信。PC机可向传感器节点发送启动、停止、配置工作模式等命令，传感器节点除了响应上述命令外，还可以将采集到的数据以及节点状态实时发送给PC。

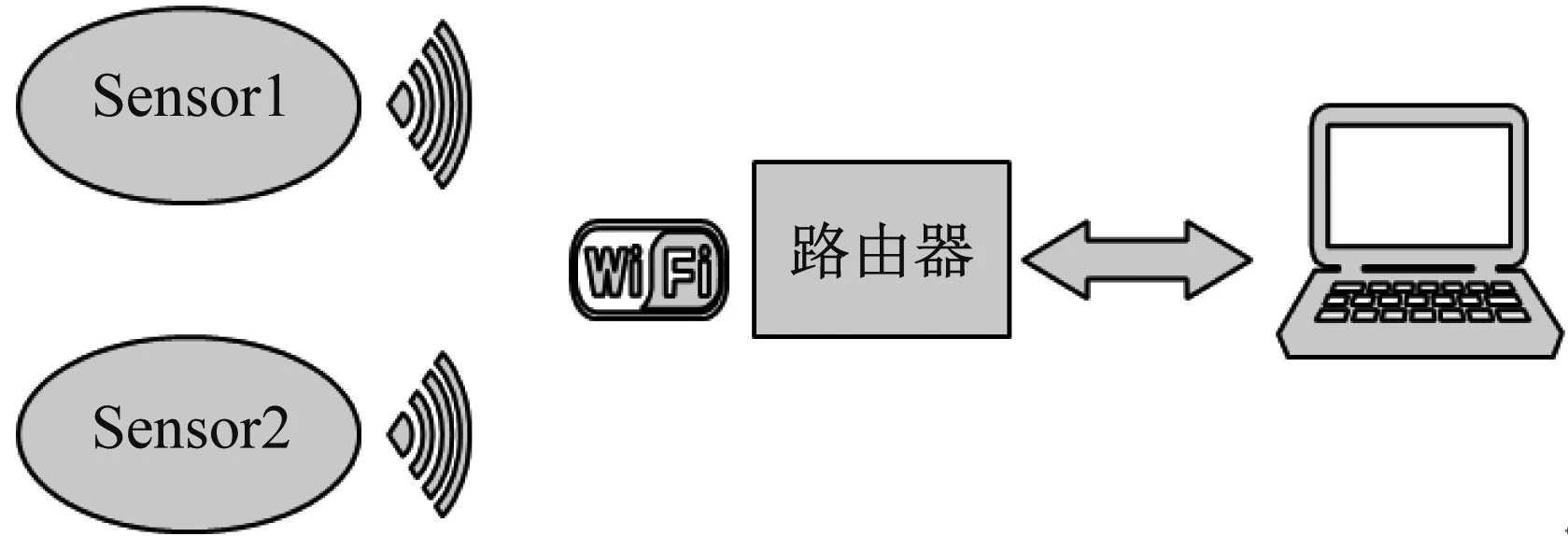
图6 无线传感系统工作原理

图7 传感器内部构造示意图

图8 集成模块示意图

实验时，传感器连接无需大量的导线连接，与常规的有线连接测试相比，安装方便，节省了大量的布线时间。在成本方面，本系统无需传统的电荷放大器和采集仪，大大降低了实验成本。本系统的使用还可避免导线振动以及连接因素等导致的测试数据的污染。

4.2 模型参数识别

由于振动台[16]的台面刚度很大，为了计算方便，将其计算模型简化为单自由度结构。对抗震实验室振动台进行空台加载，通过测量振动台台面位移，利用UKF算法识别地震模拟振动台的刚度和阻尼参数，其中外部激励荷载选取El-Centro(NS, 1940)地震波，并且假定为已知力。振动台质量已知且假定保持不变，将待识别参数初始值,见表3。

表3 待识别参数初始值

参数识别结果,如图9所示。

从图9可以看出，地震模拟振动台的刚度约为45.553 3 kN/m，阻尼约为1.540 1 kN/(m/s)。加速度实验值与位移实验值是通过实验实测得到，且与识别值吻合较好，说明刚度与阻尼识别值可信度较高。

4.3 荷载识别及改进方法

在上述已识别结构参数的基础上，假定外部激励即El-Centro地震波未知。仅以加速度(分别用无线传感器和有线传感器测得)为观测值，利用直接荷载识别法进行外荷载识别，识别结果见图10。

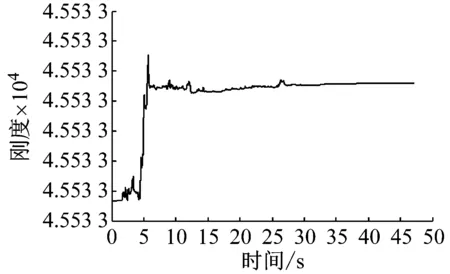
(a) 刚度识别结果

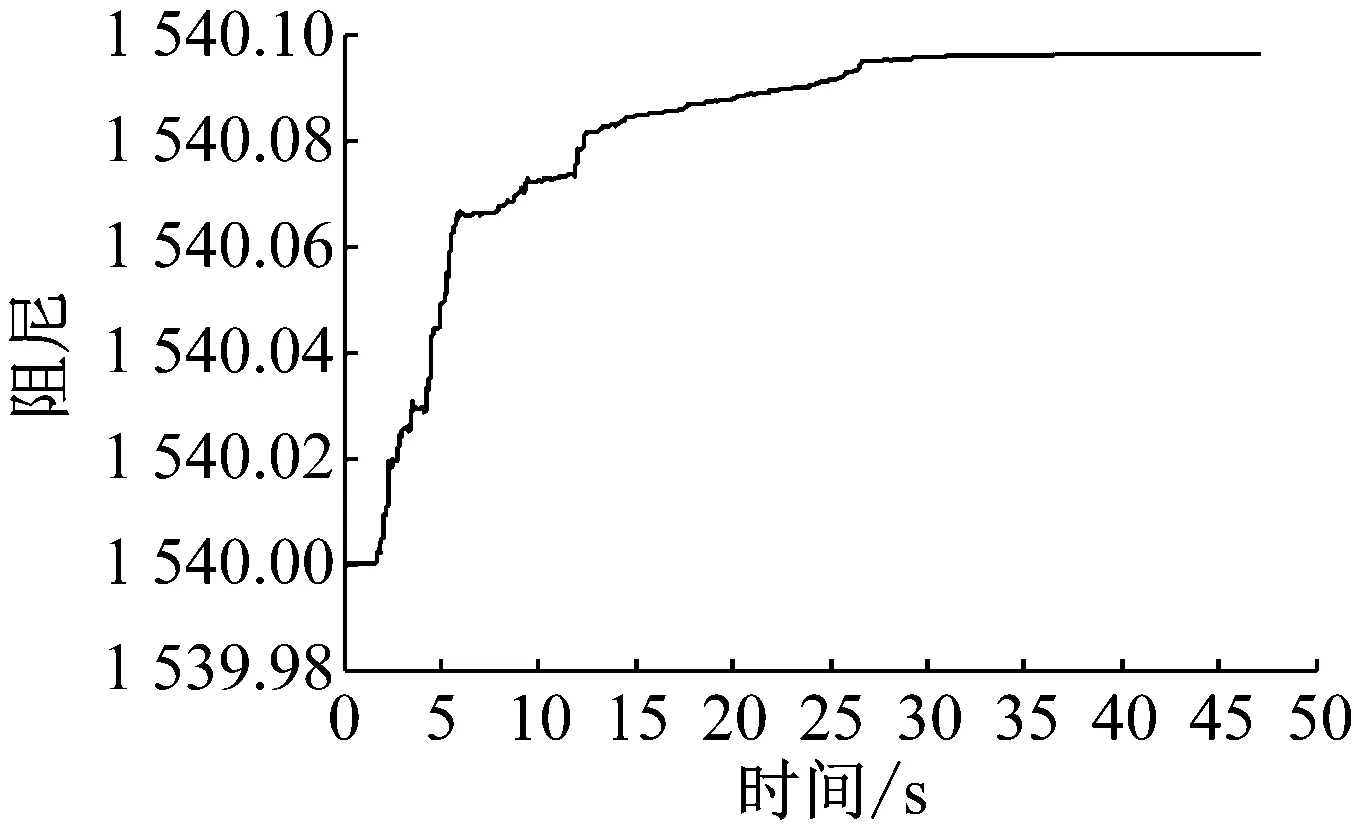
(b) 阻尼识别结果

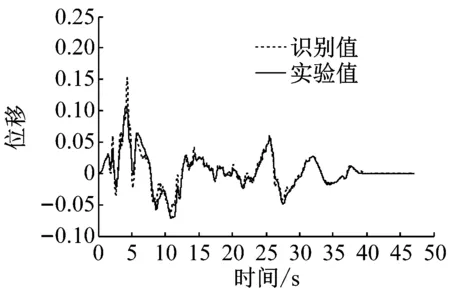
(c) 位移识别结果

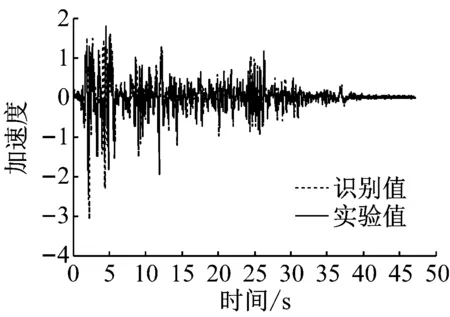
(d) 加速度识别结果

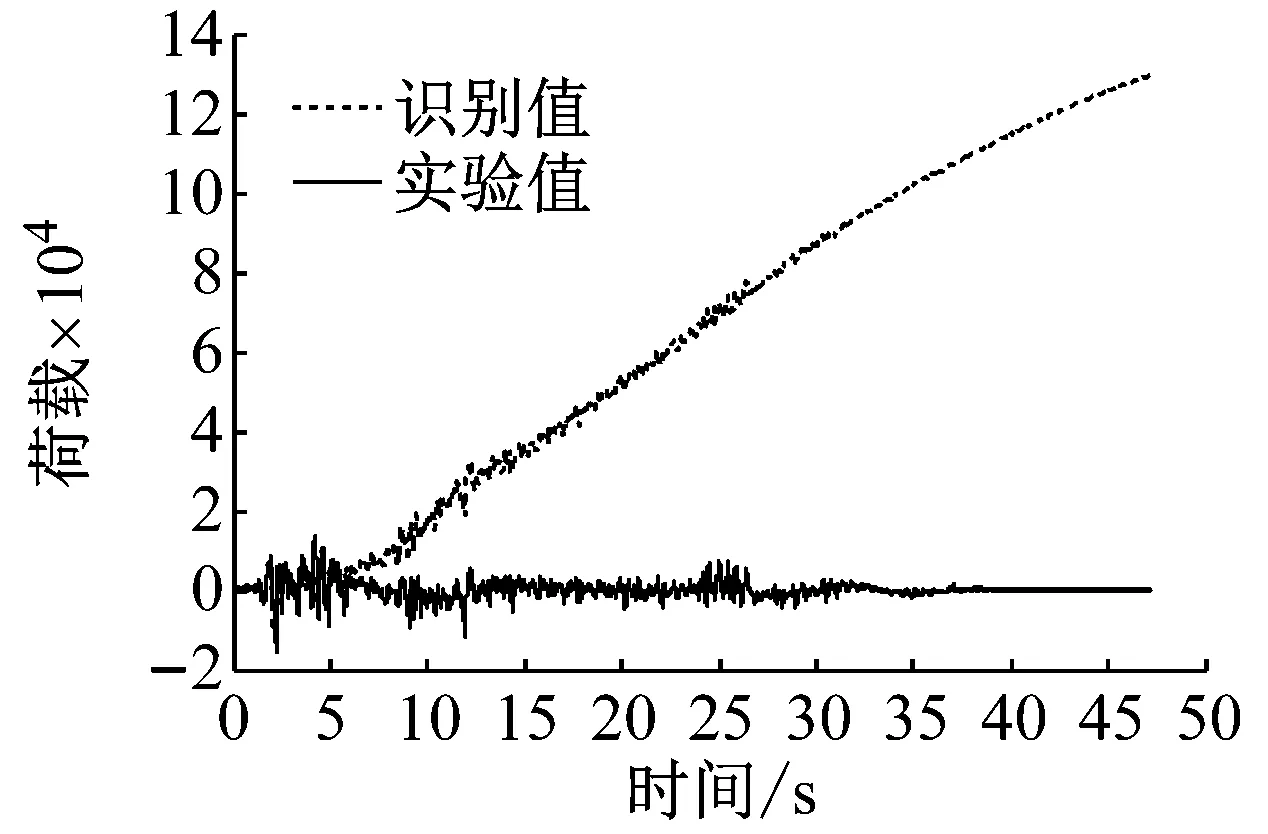
(a) 基于无线加速度的识别结果

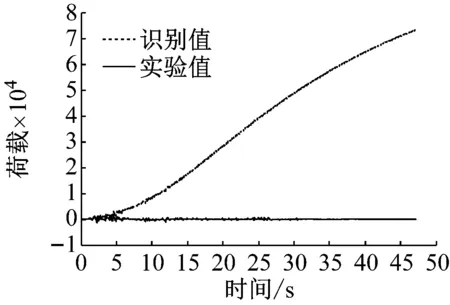
(b) 基于有线加速度的识别结果

从图10可以看出，仅以加速度作为观测值进行外部荷载识别会导致识别结果漂移，这是由于加速度值积分过程将造成误差累积，从而使识别过程不稳定，识别结果收敛性差。

针对上述漂移现象，我们提出了两种解决途径：

(1) 加速度与位移联合作为观测值

由于我们直接从实验中测得加速度值与位移值，位移值会对加速度值积分的累积误差加以约束，从而改善了识别过程的收敛性。从识别结果我们可以发现，联合位移-加速度响应下的漂移现象有了明显改善；无线加速度传感器要优于有线加速度传感器，因为有线加速度传感器的接口部位容易扰动，进而产生较大的噪声干扰。

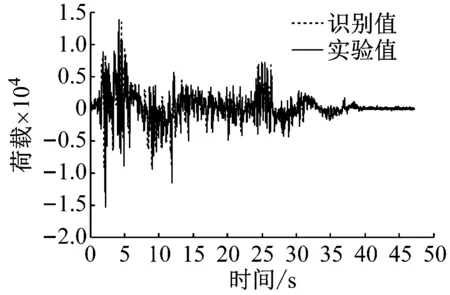
(a) 基于无线加速度-位移的识别结果

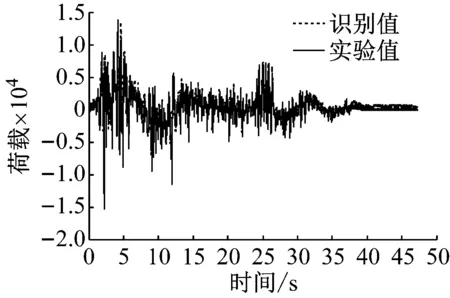
(b) 基于有线加速度-位移的识别结果

Fig.11 Identified results of external force based on acceleration and displacement

(2) 噪声水平的自适应评估

噪声水平的自适应评估指的是将过程噪声和观测噪声与原始状态量一起组合成一个新的状态量，因为当噪声太大时，UKF识别的精度不高，而且不易收敛，通过将噪声引入到状态量中，实现噪声水平的自适应评估，可以确保UKF识别过程的稳定性和鲁棒性。新的状态量如下所示：

(39)

其中增广的状态协方差矩阵变为：

(40)

除了由增广噪声构建的新的状态量和增广状态协方差矩阵的不同之外，其余计算流程均和上述UKF算法一致，且只使用加速度作为观测值。从识别结果可以看出增广噪声法改善了识别结果的稳定性与收敛性，且无线加速度识别优于有线加速度识别。

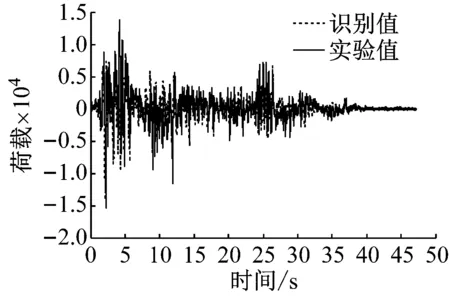
(a) 使用无线加速度的识别结果

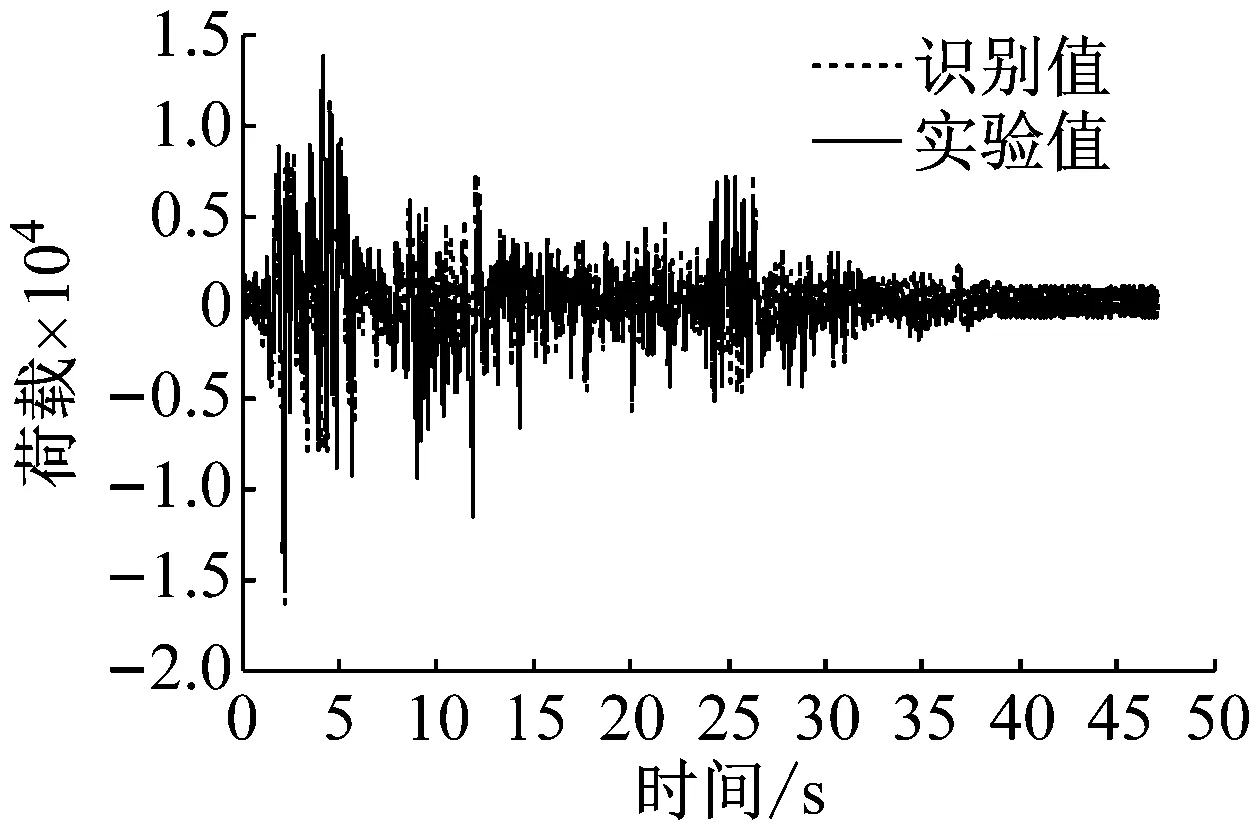
(b) 使用有线加速度的识别结果

5 结 论

本文从基于UKF算法的两种荷载识别方法出发，首先对单自由度滞回非线性剪切模型进行仿真，分别利用直接荷载识别法和基于荷载正交分解的间接荷载识别法对该模型进行两种外荷载识别，分别为周期荷载和冲击荷载。验证了直接荷载识别法应用于单自由度非线性模型荷载识别的合理性和有效性。而直接荷载识别法对于多自由度非线性模型仍是适用的，课题组人员正在从事相关领域的研究。随后利用直接荷载法对作用于地震模拟振动台上的未知地震波进行识别，并针对识别结果发生漂移的现象提出了两种直接扩展状态量的荷载识别方法，识别结果显示，两种方法对荷载识别的漂移现象有着明显的改善。