小雷诺数下弹性圆柱壳行波振动问题研究

， ，

(燕山大学 理学院 河北 秦皇岛 066004)

0 引言

工程中存在大量有关振动的问题，如海洋柔性结构的涡激振动[1-2]、大型冷却塔风致响应[3-4]、 桥梁结构的自振[5]以及水下航行器的振动[6]等.其中，水下推进器的推进机理研究日益成为科研工作者的研究热点之一，涉及海洋、船舶、核动力、机械及生物工程等多个学科.现有的主要为人工机械推进结构，如螺旋桨推进、叶轮推进、射流推进等.在推进灵活性、稳定性和效率等方面与鱼类的推进方式相比有着巨大的提高空间.根据Lighthill对水生动物的运动方式分类，波动摆动推进是其中的一类，且大部分鱼类采用该运动形式[7-8].

文献[9]建立了研究鱼类匀速直线推进的“抗力水动力学模型”，该理论模型忽略惯性力，利用鱼体与流体的静力学平衡研究鱼体的动力学，适应于低雷诺数的情况.随后，Lighthill提出“非稳态细长体理论”[10]、“伸长体理论”[11]和“大摆幅伸长体理论”[12]，用来研究柔性波动板波动推进特征.文献[13-14]考虑了板面展向变形对波动柔性板推进性能的影响，并使用波动板模型和最佳运动理论研究新月形尾的推进特性.

国内外学者对相关理论进行了广泛的研究，取得了一些成果，但由于问题的复杂性，对水中生物的推进机理还需进一步深入研究.本文尝试将水中生物看作弹性圆柱壳体，并假设圆柱壳长度足够长，且远远大于半径，将其近似为无限长圆柱壳.黏性流体中圆柱壳的摆动采用行波状运动表示，根据相容拉格朗日-欧拉法求解出的流函数表达式，计算出流体压力、单位面积上的功率以及有效作用系数等.

1 黏性流体相容拉格朗日-欧拉法基本方程

假设流体雷诺数远小于1，同黏性成分相比，流体的纳维-斯托克斯方程中惯性项可以忽略.在圆柱坐标系(r,θ,z)中，与θ无关的二维流体运动的纳维-斯托克方程近似为斯托克斯方程[15]

(1)

接触面运动方程[16]为

(2)

(3)

其中：ψ为流函数，满足rvz=∂ψ/∂r，rvr=-∂ψ/∂z；ul(l=r,z)为变形前空间点处位移矢量沿坐标轴方向的分量；R为圆柱壳半径；t为时间.

圆柱壳体表面行波振动形式为

(4)

式中：α=2π/λ；ω=cα；λ和c为波的长度及速度；Zn和Rn为振幅.

2 方程的解

式(1)中消去压力p得到方程

ψ=0，

(5)

方程(5)有解

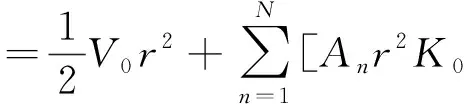
(6)

其中：An、Bn为待定参数；K0、K1是麦克唐纳函数[17]；V0是与时间无关、相对于不动坐标系无穷远处流体的运动速度，由给定问题及系数An和Bn同时确定，即相对于无穷远处不动的流体而言，壳的推进速度等于-V0.

(7)

其中：

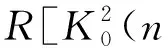
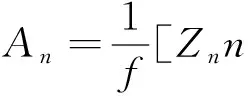
流函数得到确定.

经编程分析可知，N取值不同，计算结果的具体数值稍有不同，但变化规律一致，取N=1计算分析.由式(1)可得压力的表达式为

μ2vzdz=μ2(∂ψ/r∂r)dz，

取N=1，则

单位宽度圆柱面上，一个波长运动产生的功率[18]为

(αz-ωt)，

其中：

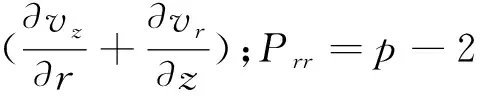
为圆柱表面上的应力[19].取N=1，可得

(8)

在αR较大时，取N=1，利用K0、K1的渐近表达式，由式(7)和(8)可得到薄板振动时无穷远处流体速度V0和功率E分别为：

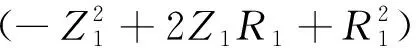
(9)

E=μω2α(R12+Z12).

(10)

薄板表面上所产生的拉力，采用近似式[20]

T=2μαV0，

(11)

将式(9)代入式(11)，得到

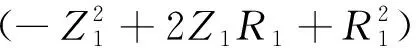
(12)

除了速度V0及拉力T之外，有效作用系数为波形运动的重要特性.按时间平均有效作用的流体动力系数，表达式[20]为

(13)

将式(9)、(10)和(12)代入式(13)，不考虑α，可得无量纲有效作用系数

.

(14)

3 结果分析

表1给出了圆柱壳以行波形式振动，振幅R1和Z1取不同数值时，壳体表面流体压力p和功率E的数值.表中未标明的参数分别取值为：ω=π rad/s，μ=1×10-2Pa·s，R=0.5 m，α=2 m-1.可以看出， 压力p主要受纵向振动振幅Z1的影响，而功率E受横向振动和纵向振动振幅R1和Z1的影响都很大.

图1 薄板振动时有效作用系数与振幅比值R1/Z1之间关系Fig.1 Relation between efficiency parameter and quotient of amplitudes R1/Z1 while the sheet vibrating

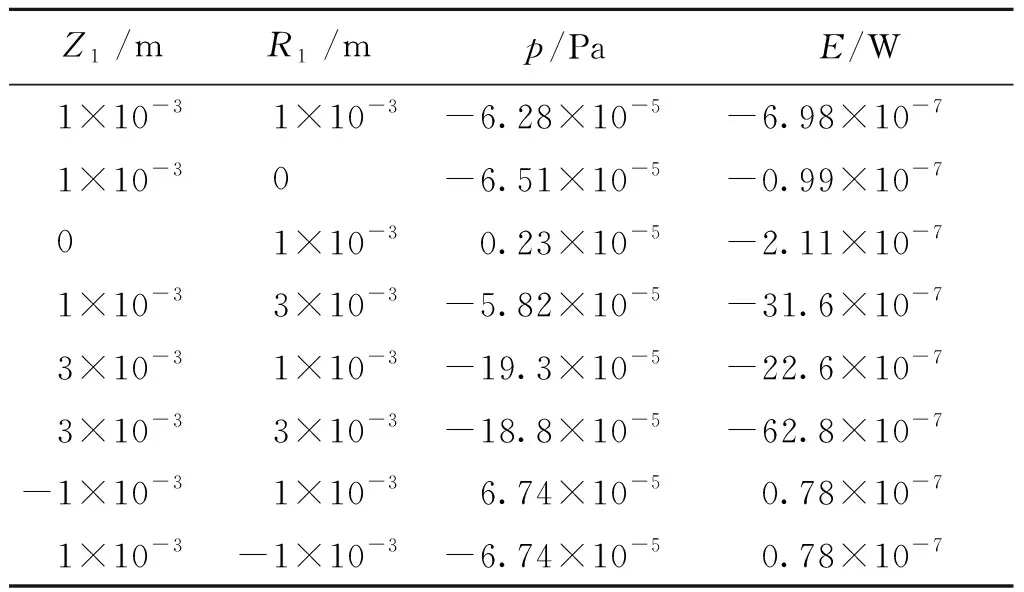
Z1/mR1/mp/PaE/W 1×10-3 1×10-3-6.28×10-5-6.98×10-7 1×10-3 0-6.51×10-5-0.99×10-7 0 1×10-3 0.23×10-5-2.11×10-7 1×10-3 3×10-3-5.82×10-5-31.6×10-7 3×10-3 1×10-3-19.3×10-5-22.6×10-7 3×10-3 3×10-3-18.8×10-5-62.8×10-7-1×10-3 1×10-3 6.74×10-5 0.78×10-7 1×10-3-1×10-3-6.74×10-5 0.78×10-7

4 结束语

本文采用相容拉格朗日-欧拉法求解弹性圆柱壳行波振动，给出了壳体的推进速度、流体压力、单位面积上的功率以及有效作用系数等，初步分析了振幅对薄板有效作用系数、圆柱壳压力和功率的影响.