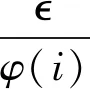基于沈峻算子的引导滤波方法研究

邢奕楠， 刘建宾

(1. 北京信息科技大学 计算机学院， 北京 100101； 2. 北京信息科技大学 软件工程研究中心， 北京 100101)

0 引言

超声成像是一种常见的成像方式，原理来源于超声波传播时遇到物体会反射或衍射的现象，它具有成本低廉，对成像物体无创无损，可实现实时成像等优点，在医学和工业领域得到广泛应用。同时，超声成像也是一种容易受噪声干扰的成像方式，会出现重要的结构或边缘信息丢失的现象。常见的超声图像去噪方法有NLM(no-local means)算法[1]、小波阈值法[2]、中值滤波[3]、维纳滤波[4]、引导滤波[5]、BM3D(block-matching and 3D filtering)算法[6]等。其中维纳滤波和小波阈值去噪方法是经典的线性滤波方法，这两种算法都是在图像内的某个邻域，利用该邻域内周围所有的像素点值来估计中心像素点值，这种局部变换的思想容易导致图像边缘或纹理等细节特征出现模糊。NLM与BM3D算法是基于块匹配思想[6]的去噪算法，它们的主观视觉效果较为优秀，但计算复杂度较高，并不符合超声图像运用场景中的实时成像需求。

保边平滑类滤波在多年的研究发展中先后出现了双边滤波[7]、引导滤波等方法。 引导滤波成功实现了保边平滑特性，可以应用在医学或工业超声图像处理领域。将引导滤波应用于超声图像去噪时，与其他局部滤波方法类似，图像的边缘经常会出现一定程度的光晕。当图像附带噪声强度较大时，这种光晕尤为明显。为了改善这种边缘光晕问题，本文引入边缘检测领域经典的沈峻算子[8](Shen-Castan)。该边缘算子可以在保证引导滤波去噪效果的前提下，提升边缘和纹理的清晰度。

在医学和工业这两个超声成像的应用场景中，引导边缘描绘是发现病灶和工件缺陷的重要方法，利用边缘检测算子来提升边缘描绘效果也是一种常用的手段。为此，本文提出了一种基于沈峻算子的引导滤波方法，该方法利用边缘检测中的沈峻算子对引导滤波进行改进，采用边缘检测结果返回的策略减轻了引导滤波结果图像存在的边缘光晕现象。实验结果表明，当超声图像噪声强度较大时，本文方法可以保持引导滤波算法原有性能，又由于边缘光晕现象的减轻，获得了一定客观评价标准指数的提升。

1 滤波算法和边缘检测算子

1.1 引导滤波

引导滤波是一种利用引导图像指导滤波过程的边缘保持算法，能够在平滑图像的同时起到保持边界的作用。引导图像与滤波器输出图像之间存在局部线性关系是引导滤波理论模型成立的假设基础[5]。常见滤波器中某像素点的输出为

(1)

而某一像素点在引导滤波中的输出为

qi=akIi+bk∀i∈ωk

(2)

式中：q为输出图像；I为引导图像；当窗口中心位于k时，a和b是该线性函数的不变系数。该方法的假设前提是：在以像素k为中心的窗口中，q和I存在局部的线性关系。通过对式(2)求导(代表边缘)可以发现，引导图像存在边缘是求导结果出现边缘的前提。

要想获得经过引导滤波的输出图像，需要求解式(2)中的系数a和b。可先假设p是q滤波前的状态，并设法实现q与p差别最小，则该问题根据无约束图像复原的方法可以转化为求最优化问题，价值函数可表示为

qi=pi-ni

(3)

求解上式这种最优化问题可以参考最小二乘法的推导过程， 式(3)的解为

(4)

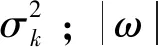
(5)

其中

(6)

从引导滤波的模型可以看出，引导图像和输出图像的线性关系包含了图像的边缘信息，即系数ak的大小代表了滤波器对图像边缘的保持能力。ak的值越小，qi中的梯度信息越少，边缘更加模糊，图像更加平滑。

1.2 沈峻算子(Shen-Castan)

Shen-Castan算子[8]是Shen等提出的具有指数脉冲响应规律的一种滤波器，它使用二阶导数滤波器的形式来检测边缘。Shen和Castan采用了经典的Canny方法[9]中边缘检测器的固定形式，即：先使用拥有平滑图像功能的高斯滤波器对图像卷积，然后再通过搜索边缘像素来确定图像边缘。不同的是，Shen和Castan对传统的边缘检测滤波器的形式进行了优化，即在一维空间上使用最小化平滑滤波器：

(7)

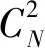
(8)

Canny算法的实现需要通过高斯导数来接近于理论中的最优滤波器，而Shen-Casten算子直接使用最优滤波器。在二维空间中，ISEF为

f(x▯y)=a·e-p(|x|+|y|)

(9)

式中“▯”符号为滤波器在二维空间内的递归滤波操作式。式(9)同高斯滤波器中的导数一样可直接应用于图像，即在x方向与y方向上作为一维滤波器。该滤波器在Shen-Castan的理论模型中被设计为一维递归滤波器。上面的滤波器函数f是一个真实的连续函数，它可以被重写为离散采样形式：

(10)

以上是Shen-Castan算子理论模型中滤波器的原理，而实际对图像的滤波过程依次还包含了递归滤波、定位边缘、阈值处理这些提升综合效果的过程。具体步骤如下：

1)递归滤波。采样形式被标准化之后，此滤波器被用来对图像进行卷积。首先在x方向上进行递归滤波，得到r[i，j]：

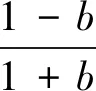
1，2，…，N▯i=1，2，…，M

j=N…1▯i=1，2，…，M

(11)

r[i▯j]=y1[i▯j]+y2[i▯j+1]

其中边界条件为：

I▯[i▯0]=0

y1[i▯0]=0

(12)

y2[i▯M+1]=0

然后在y方向上进行滤波，滤波器的最终输出结果y[i，j]为：

1，2，…，M▯j=1，2，…，N

N…1▯j=1…N

y[i▯j]=y1[i▯j]+y2[i+1▯j]

(13)

边界条件为：

I▯[0▯j]=0

y1[0▯j]=0

(14)

y2[N+1▯j]=0

递归滤波加速了滤波器对图像的卷积，以快速得到滤波后的图像。

2)边缘定位。滤波后的图像可以通过寻找拉普拉斯算子的零交叉来定位边，即非过零抑制机制[10]。这是一种类似于Canny算法中非极大值抑制的方法：滤波图像的边缘像素存在二阶导数零交叉的现象，即该点的梯度可以是最大值或最小值。如果二阶导数由正变负，则称为零交叉；如果它由负变正，则视为非零交叉。零交叉位置梯度值为正，非零交叉位置梯度值为负。

假设除了边缘像素，其他位置不存在零交叉现象，从平滑图像中减去原始图像可以快速获得拉普拉斯算子的近似值：

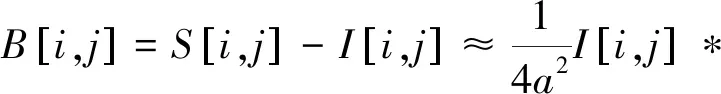
(15)

式中：I为原始图像；S为过滤后的图像；B为图像中的有限制—拉普拉斯算子[11]。由此，可以通过将B中的所有正值像素设置为1，其他像素设置为0来获得二进制拉普拉斯图像，图像区域边界上候选边缘像素所对应的零交叉位置即为边缘。

3)阈值处理。步骤2)定位的边缘是由零交叉标记过的边缘像素点组成，也叫强边缘，即它们其实就是由图像中真正的边缘提取而来。

而真实边缘提取过程中的像素误差或图像噪声、颜色变化会形成弱边缘，即非真实边缘的纹理特征。按照科学实验追求精确的原则，应该抑制弱边缘像素来得到更清晰精准的图像边缘。

2 改进算法

2.1 算法思路

在传统的引导滤波算法中，输出图像中某一点的像素值是由周围9个或9个以上像素点局部滤波之后取平均值得到的[13]。在式(2)中，ak的值代表对图像边缘的保持能力，每一个局部窗口都有不同的ak与之相对应，这使得引导滤波算法本身就具有一定的边缘检测能力。但是，式(4)中正则化系数对所有局部窗口图像边缘保持度的约束力度都是相等的，这是导致引导滤波边缘位置出现光晕情形的根本原因。

超声技术在医学场景下的应用主要在于对病灶器官部位的观察，多边缘信息的成像结果有利于识别和确定病灶位置；在工业领域，超声技术经常应用于无损检测，多纹理信息的成像结果有利于确定工件坏损位置和大小。如果要将引导滤波应用于这些实际应用场景，就需要利用优秀的边缘检测技术改善原有图像在去噪后视觉效果模糊或出现光晕的现象。

沈峻算子是边缘检测领域中一种经典的方法，式(15)中零交叉方法与边缘阈值法的应用使得图像边缘位置确定得更加准确；且有学者经过参数分析与实验对比，提出：噪声强度较大时，沈峻算子在二维空间的最优指数滤波器f(x▯y)比传统Canny算法中的高斯导数滤波器在现有图像去噪效果客观指标上的表现更好[11]。这也是本文将沈峻算子(Shen-Castan)作为超声场景下改善引导滤波算法的理论依据。本文正是基于这一理论基础展开了研究与实验。

2.2 算法实现

散斑又称为斑点噪声，是一种局部相关的乘性噪声。它破坏了超声的成像效果，研究人员Burckhardt 描述了斑点噪声的基本模型[14]：

yi,j=xi,jni,j+ai,j

(16)

式中：yi,j为位于移动窗口中心区域的噪声像素；xi,j为无噪声像素；ni,j和ai,j分别为乘性噪声和加性噪声；i,j为二维空间的位置标识，i,j∈R2。在实际超声图像生成的过程中，存在射频信号包络检测、对数压缩等影响扫描器内部的原始信号处理的操作；另外，部分文献发现对数压缩在超声波高强度区域比在低强度更多地影响到瑞利和Rician概率密度函数的分布[13]，这导致斑点噪声变得非常接近于未压缩瑞利信号的白高斯噪声。

处理上述噪声的算法实现过程如下：

已知存在一幅噪声图像y=x+n，其中y为真实的含噪声图像，x为待恢复的干净图像，n代表均值为0、标准差为σ的白高斯噪声。

第1步对噪声图像y进行Shen-Casten算子边缘检测得到结果e；

第2步将结果e返回到原始图像中得到边缘增强的引导图像I；

第3步将I作为引导图像，对y进行引导滤波，输出最终引导结果p。

本文算法的流程如图1所示。

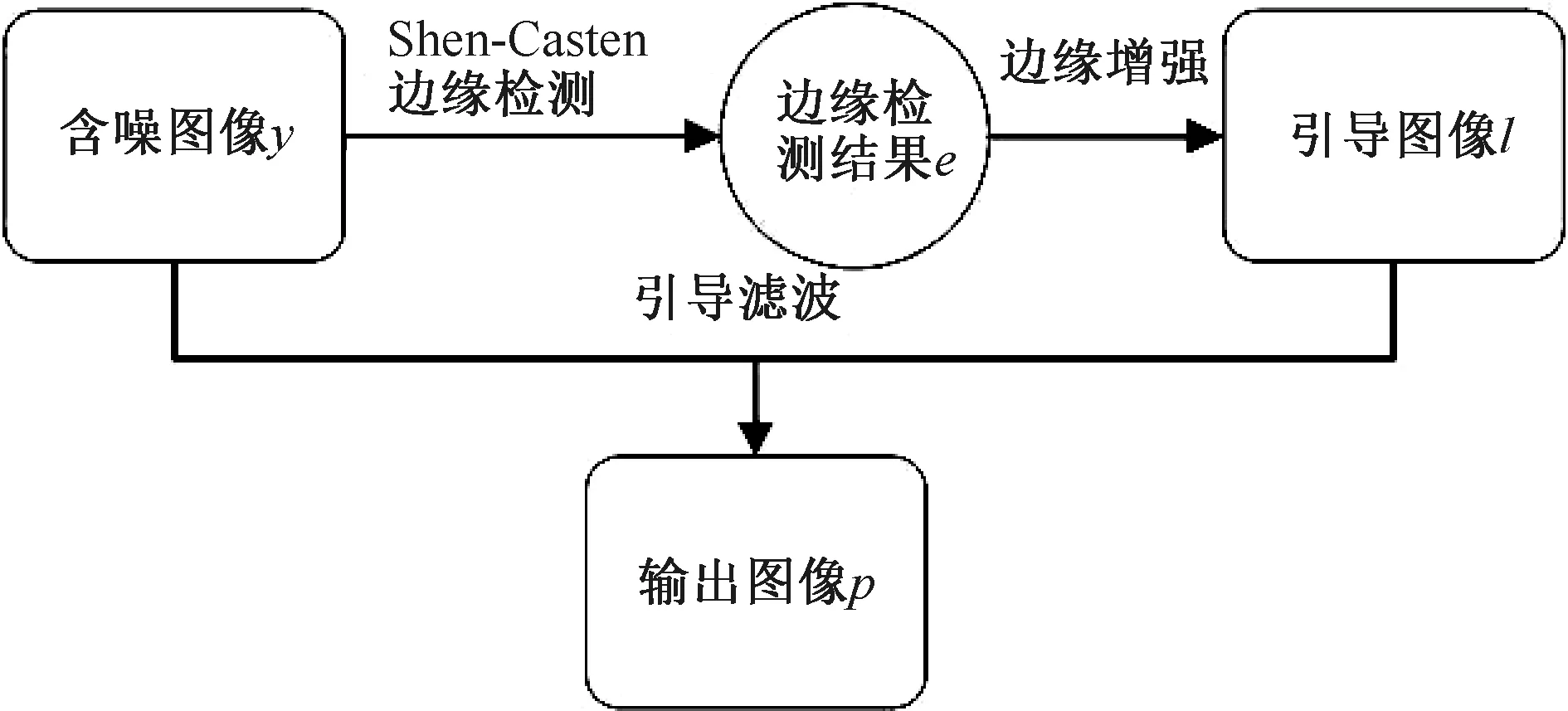
图1 本文算法流程

2.3 算法复杂度分析

滤波算法的复杂度则是体现可实现性的重要参数。沈峻算子边缘检测的步骤可划分为递归滤波、边缘定位和阈值处理3个步骤。其中步骤1和2中用到的梯度方向计算公式以及非过零抑制机制都是通过对固定大小领域(内核)的图象进行卷积来实现的，使用快速傅氏变换(FFT)进行图像卷积的时间复杂度为O(nlbn)，其中n是像素的数量；如果图像具有m×n维度，则这些步骤的时间复杂度将是O(mnlbmn)。步骤3为边缘阈值处理，这一步可以在O(mn)内实现。故沈峻算子边缘检测的总时间复杂度为O(mnlbmn)。

引导滤波的一个主要优点是它具有O(N)的时间复杂度[15]。局部窗口的大小实际上并不会影响它的时间复杂度。故不论局部滤波的邻域(内核)有多大或多小，引导滤波算法的时间复杂度都不会发生改变。

其他常见的图像去噪算法还有小波、中值滤波、非局部均值去噪等方法。小波去噪(主要为软阈值法)的算法时间复杂度为O(N)，其中N为信号长度。这种方法的阈值选择对去噪效果有很大的影响，需要根据实际情况来对阈值进行选择。中值滤波的算法复杂度为O(n2)，非局部均值(NLM)是一种利用滑动框来搜索取值的去噪算法，对于一幅有n像素点的图像，搜索窗口为D×D，邻域大小为d×d，计算邻域相似度的复杂度为O(d2)，计算带搜索窗口的领域的复杂度为O(d2D2)，整个算法复杂度为O(Nd2D2)。

通过以上算法复杂度分析可以得出：本文提出的改进算法复杂度适中。

3 仿真实验及参数分析

为了更好地对比本文算法与其他算法的去噪效果，本文同时采用洛桑大学(University de Lausanne)开源医学超声数据库中的胸部肿块图像和中国科学院大学的工业超声图像(显卡芯片内部结构)进行实验仿真。选择PSNR和SSIM作为衡量图像处理水平的标准。将引导滤波算法和基于沈峻算子的引导滤波算法分别与文献[1]提出的NLM去噪,文献[2]提出的小波阈值去噪以及文献[3]提出的中值滤波方法进行对比分析。并且在两种超声处理场景下，对不同噪声水平的(σ=10,20,30,40；σ为噪声标准差)的图像进行了仿真实验。表1和表2分别呈现了被测试图像的PSNR与SSIM。图2～5为仿真实验的图像输出结果。

从表1、2可以看出，在噪声标准差为30及以上时，本文提出的改进引导滤波方法比目前常用的一些图像去噪算法，在峰值信噪比和结构相似度上有更好的表现。在噪声标准差为20及以下时，NLM算法的PSNR值最高，中值滤波的SSIM值最高。这说明NLM算法去噪效果较为可观，但在边缘保持度上不够理想；中值滤波有较为优秀的边缘保持效果，但去噪能力不强。

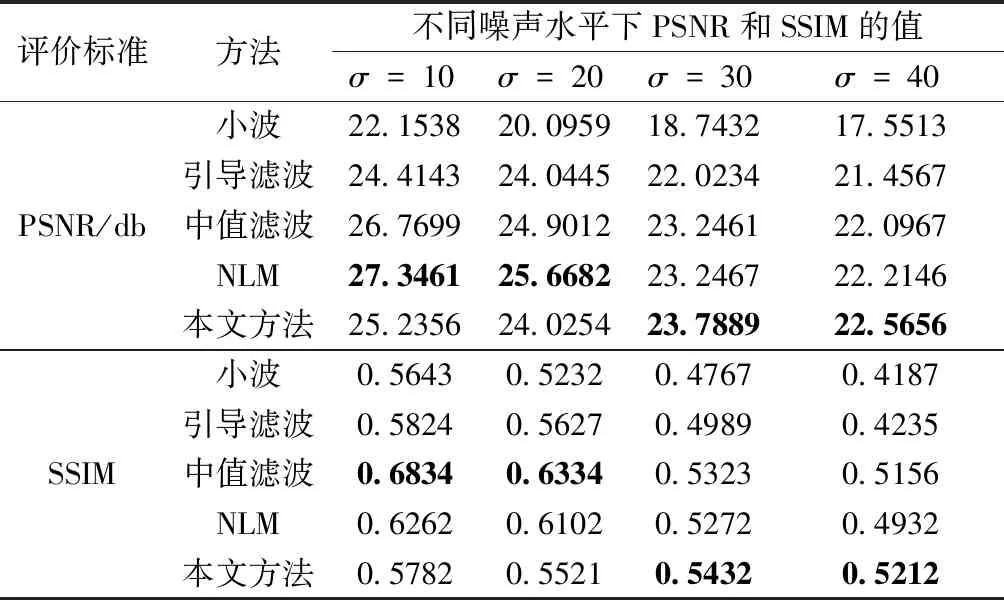
表1 胸部超声图像的PSNR和SSIM值

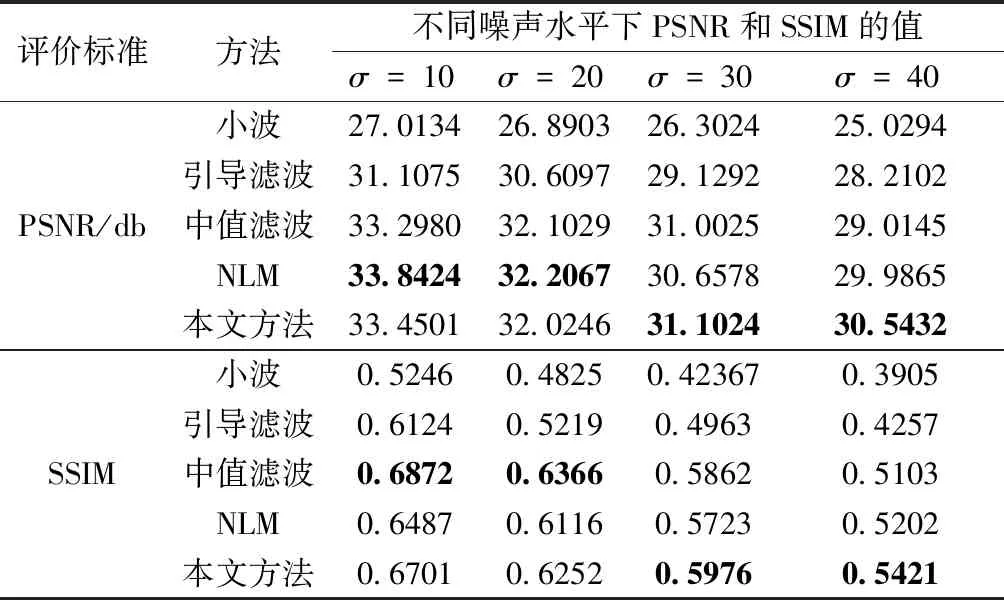
表2 工业超声图像的PSNR和SSIM值

图2展现了医学超声应用背景下，不同去噪算法在不同噪声水平下的主观去噪结果；图4展现的是工业超声图像应用背景下，不同去噪算法在不同噪声水平下的主观去噪结果。可以发现，引导滤波的边缘出现了预想中的光晕现象；小波阈值去噪的主观视觉效果较为平庸；NLM算法由于其算法的高复杂度呈现出良好的去噪表现。图3和图5分别表现了两种应用场景下边缘细节的放大图，可以看出本文方法在一定程度上减少了传统引导滤波中常出现的边缘光晕现象，不论是主观还是客观评价标准都获得了提升。

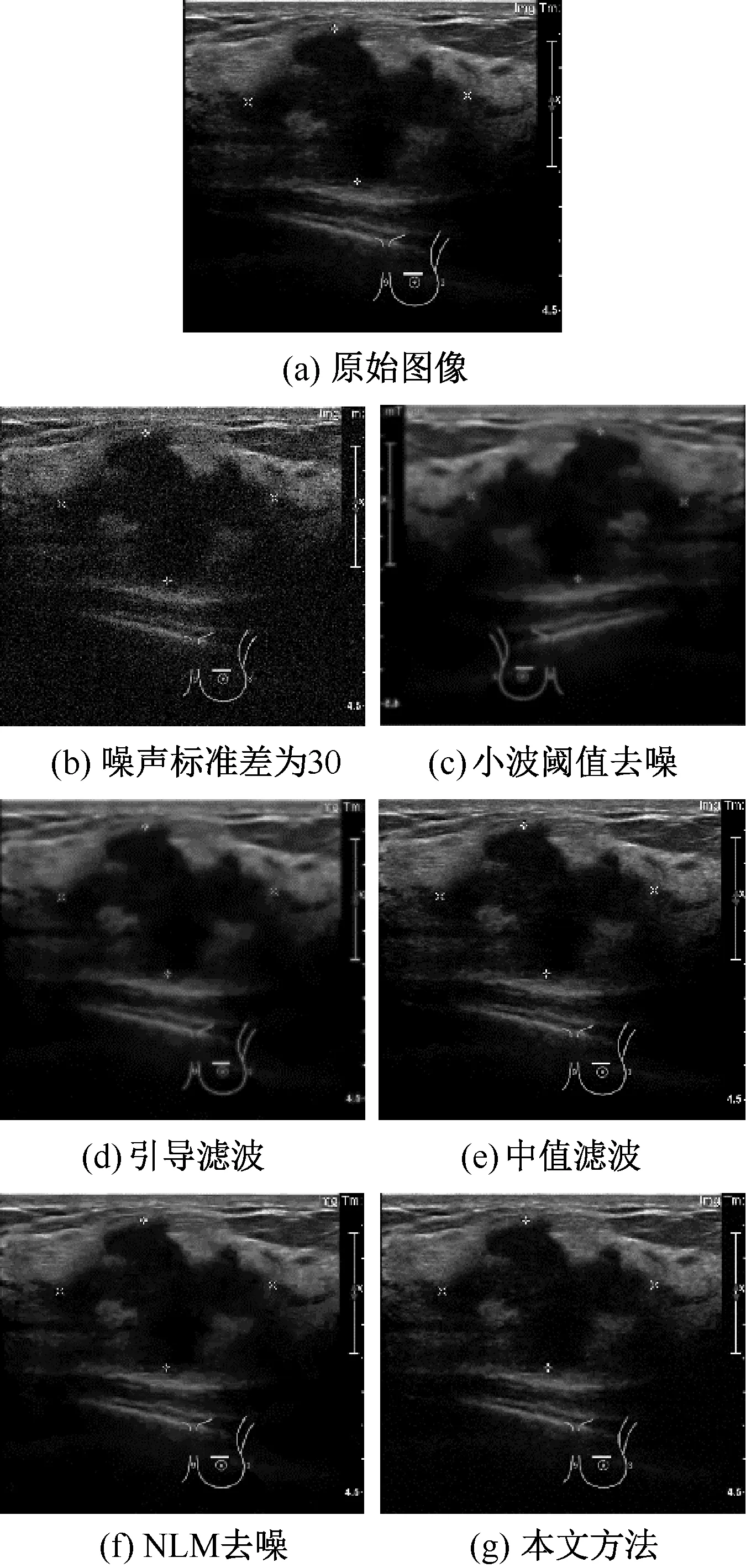
图2 不同算法对胸部超声图像的效果对比

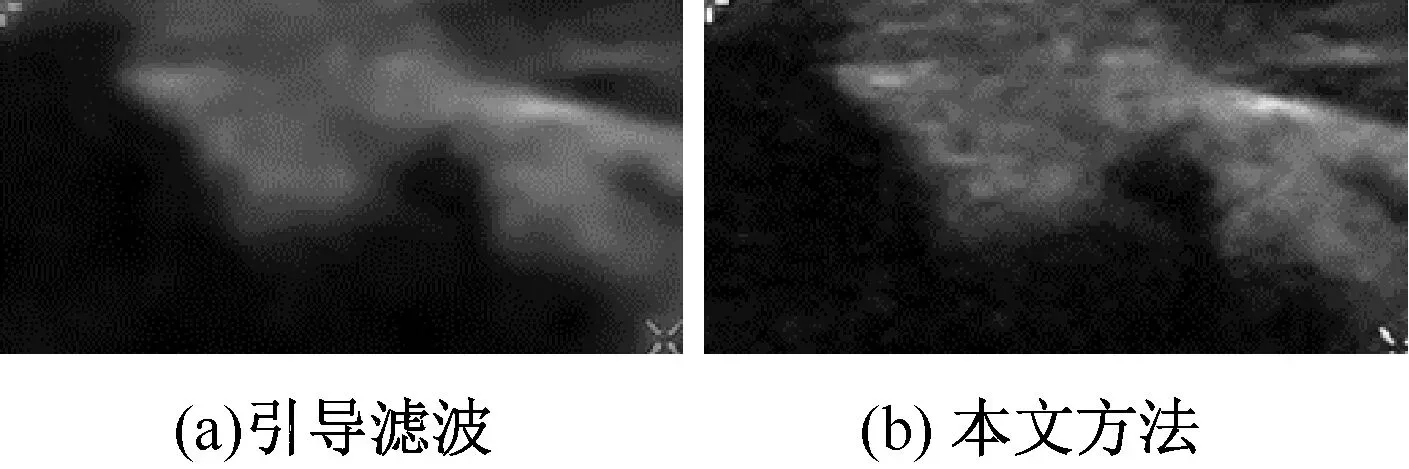
图3 传统引导滤波和本文方法在胸部超声图像下的细节放大图

图4 不同算法对工业超声图像的效果对比图

图5 传统引导滤波和本文方法在工业超声图像下的细节放大图

4 结束语