国外轴对称再入飞行器中段机动策略研究

熊 伟，张艳玲，姜 利，宋剑爽，王 智

（北京宇航系统工程研究所，北京，100076）

0 引 言

传统轴对称再入飞行器的飞行过程通常可以划分为主动飞行段、自由飞行段（也称飞行中段）以及再入飞行段，其飞行弹道的特点是主动飞行段之后的弹道为固定的、不作机动的惯性弹道，且自由飞行段时间长[1]、飞行速度相对再入飞行段较低。正是这一特点，使得可以利用现有的高科技手段，在很短的时间内预测出轴对称再入飞行器的弹道，并对其进行拦截。此外，传统轴对称再入飞行器对飞行中段可能遭遇到的空间碎片交汇碰撞亦显得无能为力。因此可通过在传统轴对称再入飞行器上增加躲避机动级，使轴对称再入飞行器在主动段结束之后的飞行中段实施自主机动变轨，达到“保存自己”的目的[2]。相对于其它飞行段，飞行中段机动变轨的好处是，没有大气的影响，飞行工况相对较好，且由于飞行速度相对较低，机动效率会相对较高、节省能量。这样轴对称再入飞行器在飞行中段不再是一个无动力的惯性飞行器，而是带有动力系统、控制系统和探测系统的智能躲避机动飞行器，通过在飞行中段进行程序机动来改变飞行弹道，使弹道不可预测，或压缩对方拦截防御系统的反应及拦截时间，增大拦截难度，提高轴对称再入飞行器的生存概率；即使程序机动之后，仍被对方拦截弹跟踪，亦可通过在交汇段实施躲避机动来提高自身生存概率。虽然国内外关于飞行中段机动变轨规划策略的研究较多[3～5]，但考虑的机动变轨过程相对简单，没有针对飞行中段全剖面的机动策略进行研究。为此，本文以国外三级运载器+液体躲避机动级为对象，对其在飞行中段全过程的机动规划策略进行研究，并给出相应的仿真算例。

1 中段机动规划问题的数学模型

1.1 约束条件

轴对称再入飞行器中段机动规划的主要约束条件如下：

a）能量规划建模。

1）能量约束。

将用于程序机动的推进剂分配成N次机动使用，选择N次机动所消耗的推进剂需满足如下约束：

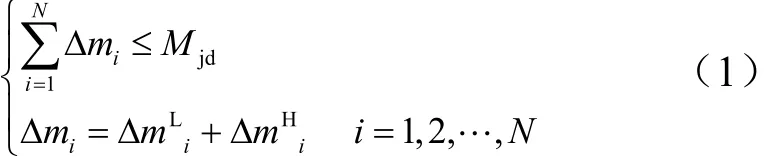
式中 Δm为第i次程序机动分配的能量；Δ mL为第i

i

i次程序机动，进行纵向机动的能量分配； Δ mHi为第i次程序机动用于横向机动的能量分配；Mjd为程序机动可用的推进剂总量。

2）落点约束。

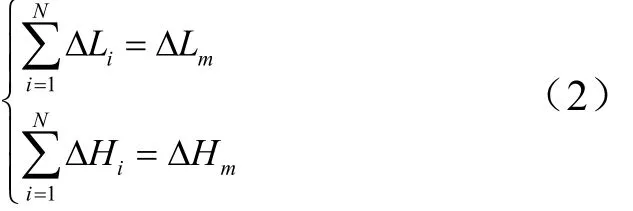
式中iLΔ为第i次程序机动的纵向机动距离；mLΔ为不作机动的惯性弹道落点与实际目标点之间的纵向偏差；iHΔ为第i次程序机动的横向机动距离；mHΔ为不作机动的惯性弹道落点与实际目标点之间的横向偏差。

3）机动时间约束。

机动的时间点选择对生存效果有很大影响，时间越早，则弹道机动引起的落点变化范围越大；时间越晚，则有利于压缩对方拦截防御反应时间，但是会减小弹道机动引起的落点变化范围。因此，机动时间点的选取，需要权衡这两方面因素。

b）再入条件约束。

机动规划时确保飞行器再入模拟量不超过设计要求值。

c）飞行程序设计约束。

考虑到控制系统姿态跟踪能力，在弹道设计时飞行程序角变化率应小于控制系统设定的指标值cx0ϕ。

d）落地马赫数约束。

式中 Ma为落地马赫数；a0M 为设计指标要求的最低落地马赫数。

1.2 大气层外飞行的弹道计算模型

弹道计算模型采用三自由度的质点弹道计算模型，输入为飞行中段机动变轨时刻的俯仰、偏航程序角，输出为速度、位置等弹道参数，主要包括动力学模型、地球及大气模型和发动机模型，具体如下：a）动力学模型：采用航天工业部标准 QJ1477-1988质点动力学模型；b）大气模型：采用国军标GJB 365.1-1987里的标准大气模型；c）地球模型：考虑地球自转和扁虑的影响，采用航天工业部标准QJ907-1985里的标准地球参数；d）发动机模型：程序机动以及躲避机动采用小推力液体发动机，可多次关闭和启动，其产生的推力和秒耗量按常值处理，程序机动过载按0.6g考虑，躲避机动过载按6g考虑。

2 飞行中段程序机动策略

通过飞行中段程序机动设计可以实现2种不同的机动效果：a）变落点方式，即程序机动过程中不仅改变飞行弹道轨迹，同时预示落点也在改变；b）变弹道程序机动方式，即程序机动仅改变飞行弹道轨迹而不改变落点。

变落点方式的程序机动方法很多，如正余弦机动、梯形机动、三角波机动、方波机动、随机机动、蛇形机动[6]等。在这些程序机动方法中，正弦程序机动比较典型，具有代表性。相关研究证明，再入飞行器在平面内作正弦机动时，脱靶量最大[7，8]。因此本文以侧向正弦程序机动方法为例，研究侧向程序机动引起的纵、横向增程距离与偏航程序角幅值、程序机动分配的能量及程序机动起始时间之间的关系，构建其映射函数。

侧向正弦形式的飞行程序角可以表示为

式中cxψ为程序机动时的偏航程序角；jdT为程序机动当前实际飞行时间（以程序机动起始时刻为计时零点）；R为幅值；jt为本次程序机动总时间；0f为初始相位角。通过改变上述变量可以得到不同的落点轨迹。

当机动飞行时间与jt相等时，程序机动程序角为一个完整的正弦曲线，不相等时则可得到不同周期的程序角，相应的落点轨迹为全周期的一部分，通过改变程序角幅值可以得到不同形状的落点轨迹。图1为不同的偏航机动幅值对应的落点轨迹。

图1 不同偏航程序机动幅值对应的落点轨迹示意Fig.1 Tracks of the Descent Point Corresponding to the Different Amplitudes of Maneuvering Angle in Yaw Procedures

由图 1可知，通过控制机动幅值可以得到不同的纵横向机动距离。

图2为不同的偏航机动初始相位角对应的落点轨迹.由图2可知，通过改变初始相位角可以保证在落点基本不变的情况下得到不同的落点轨迹。

图2 不同偏航程序机动初始相位角对应的落点轨迹Fig.2 Tracks of The Descent Point Corresponding to the Different Initial Phase of Maneuvering Angle in Yaw Procedures

通过对侧向正弦程序机动典型模式的分析，可得到程序机动引起的纵、横向机动距离与偏航程序角幅值、程序机动分配的能量及程序机动起始时间之间的映射关系。由于这些映射关系存在较强的非线性，因此可通过建立插值表或分段拟合的方法构建映射关系。

根据程序机动距离的变化规律，三级关机后的躲避机动级弹道设计主要包括以下步骤：

a）建立不同射程、不同射向下侧向程序机动引起的落点纵、横向变化距离dL和dH与标准状态（GJB 6270-2008对标准状态有明确定义）不作机动的惯性弹道的理论落点对应的标准射程（简称标准射程）、射向 A0、发射点纬度 B0、标准状态下程序机动引起的落点纵、横向变化距离、的函数关系，具体公式如下：

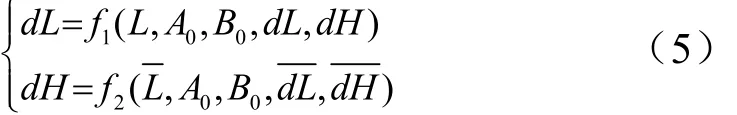
c）根据式（5）、式（6），建立如下方程：

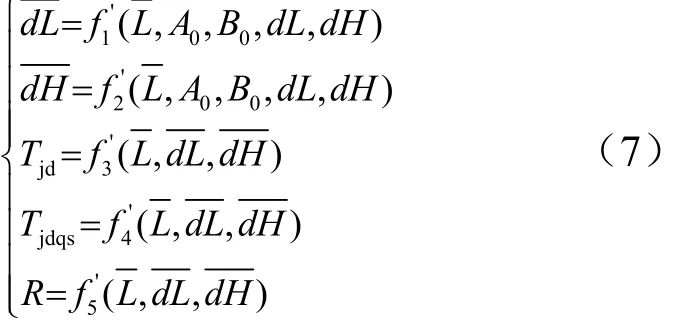
式中 f'( )为 f ( )的反函数。

完成上述映射关系构建后，即可按如下步骤进行躲避机动级机动规划：

a）判断主动段结束之后不作机动的情况下惯性弹道的理论落点是否在目标点附近。

b）若不作机动的情况下惯性弹道的理论落点在目标点附近，且程序机动的目的是为了规避与无自主机动能力的太空垃圾发生碰撞，则躲避机动级能量可全部用于程序机动，程序机动策略可选择变弹道程序机动方法，如躲避级发动机推力线方向始终指向零射程线方向[9]，此时可改变弹道但不改变落点，尽可能节省弹道回归所需推进剂。

c）若不作机动的惯性弹道的理论落点离目标点较远或程序机动的目的是为了躲避对方拦截飞行器的拦截，则躲避机动级能量除了用于程序机动，还必须用于将再入飞行器落点修正到目标点，此时程序机动模式选择变落点程序机动方法，包括以下步骤：

1）根据不作机动的惯性弹道的理论落点和目标点信息解算落点纵横向偏差距离dL，dH；

2）利用落点纵横向偏差距离dL，dH，不作机动的惯性弹道的理论落点对应的标准射程L、射击方位角 A0、发射点纬度求解所对应的标准状态增程距离，即：

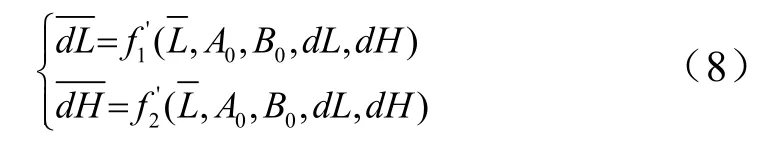
3）利用标准射程L、标准状态下程序机动引起的落点纵、横向变化距离dL和dH，求解程序机动幅值、程序机动时间、程序机动起始时间的初值，即：

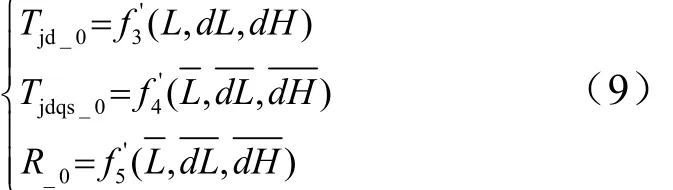
4）以求解的程序机动幅值 R_0、程序机动时间Tjd_0、程序机动起始时间 Tjdqs_0为初值利用牛顿迭代法等快速优化算法求解准确命中目标点的程序机动幅值、程序机动时间、程序机动起始时间。

5）针对牛顿迭代法求得的结果进行一次弹道仿真，检验是否满足1.1节列出的全部约束条件，如果不满足，则调整机动策略，重新进行弹道设计与迭代求解，直至满足全部约束条件为止。

3 交汇段躲避机动策略

如果中段程序机动失效，对方发射外大气层截杀载具（Exoatmospheric Kill Vehicle，EKV）飞行器进行拦截，则需要采取躲避机动策略进行躲避。通过分析，最优躲避机动策略为：在交汇段躲避机动级探测到EKV后，按垂直于EKV来袭方向进行大角度快速调姿，调姿到位后进行大过载加速飞行，以躲开EKV的直接碰撞。理论上存在无数个垂直于EKV来袭方向，为了提高躲避机动效率和生存概率，躲避机动级需要往最优躲避能量方向进行快速调姿。

交汇段规避示意如图3所示。由图3可知u为最优躲避能量方向，该方向可由下式确定：

式中 V1为EKV拦截飞行器来袭速度；V为躲避机动级当前速度。

式中axu ，ayu ，azu为u在发射惯性下的3个方向的分量。由于V1和V2是已知的，因此交汇段调姿程序角可按上式求解。

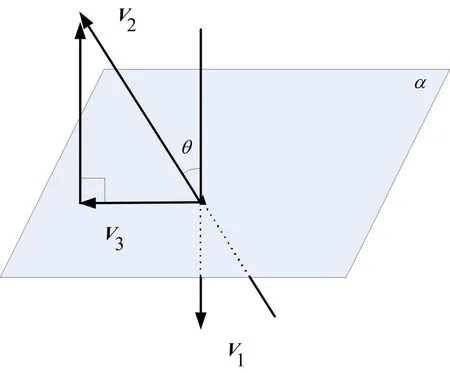
图3 交汇段躲避示意Fig.3 Sketch Map of the Escaping Maneuver in Intersection Phase α—垂直于V1的平面；V3—V2在平面α上的分量；V1—EKV拦截弹来袭速度矢量；V2—躲避弹头当前速度矢量；θ—当前交会角

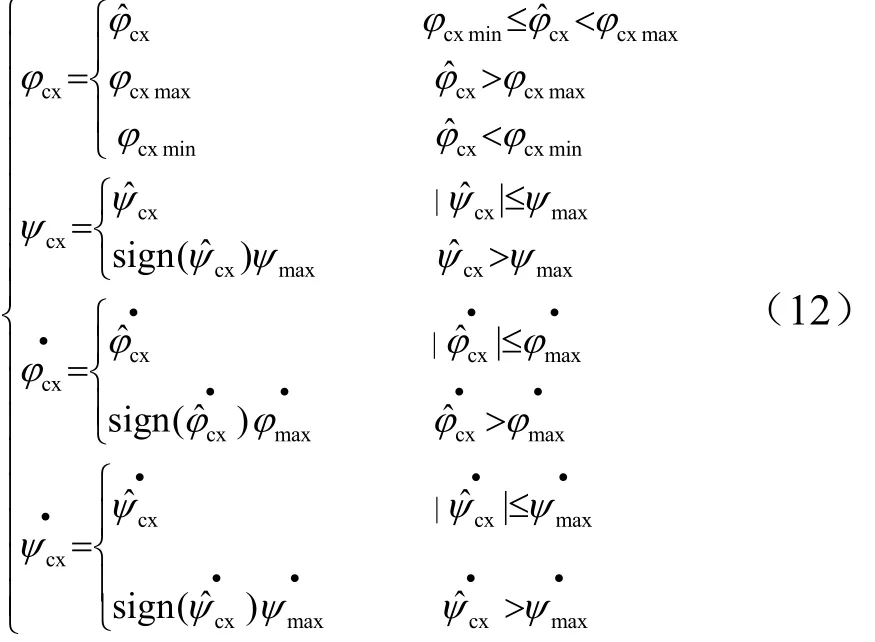
式中 ϕcxmax，ϕcxmin，ψmax分别为俯仰、偏航程序角限幅值；ϕmax，ψmax分别为俯仰、偏航程序角速度限幅值。

4 弹道回归机动策略

在完成飞行中段程序机动及交汇段躲避机动后，弹道落点通常与原目标点存在一定的偏差，此时需要躲避机动级基于剩余的能量，进行弹道机动回归，确保躲避机动级仍能落入原目标点或落入新选目标点，具体策略为：

a）无动力滑行一段时间，既能误导对方将当前的惯性落点当成躲避机动级的最终目标点，降低或消除其可能进一步采取防御或拦截措施的有效性，又能在这一段时间里根据当前的速度位置以及剩余推进剂，快速规划躲避机动级再入的地面落点最大可达区域范围，并判定原目标点是否在该范围内；

b）若原目标点在躲避机动级再入的地面落点最大可达区域范围内，则可采取闭路制导方法确保躲避机动级最终落入原目标点，实现弹道回归机动；

c）若原目标点不在躲避机动级再入的地面落点最大可达区域范围内，则可在该范围内选择新的目标点，仍然采取闭路制导方法确保躲避机动级最终落入新选目标点。

需要说明的是，如果对轴对称再入飞行器的再入条件约束要求比较严格，则可将再入条件约束引入到闭路制导方法里。

5 仿真算例

以俄罗斯白杨-M 导弹为轴对称再入飞行器的前三级基础级，以文献[4]给出的机动弹头模型参数作为躲避机动级，以该再入飞行器从朝鲜的平壤飞往目标点T为攻防对抗仿真实例，考虑拦截器近距拦截时，交汇点约为1300 s，在相距200 km左右时，防御方EKV来袭方向相对轴对称再入飞行器弹体坐标系高低角约为-18°，方位角约为-13°，相对速度为-10000 m/s，2000 m/s，3000 m/s。

5.1 弹道规划方案

a）飞行程序角。

弹道规划的飞行程序角曲线如图4和图5所示。

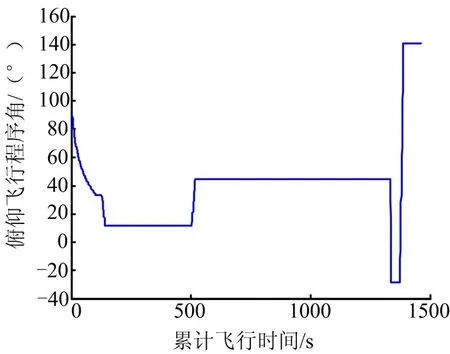
图4 俯仰方向飞行程序角曲线Fig.4 Flight Angle Curve in Pitch Direction

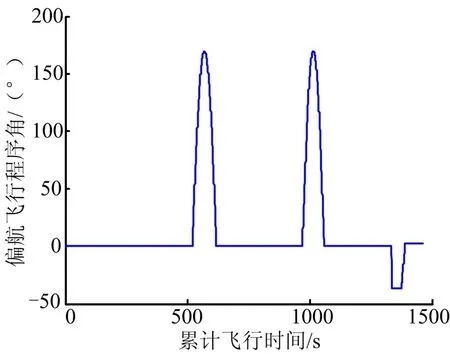
图5 偏航方向飞行程序角曲线Fig.5 Flight Angle Curve in Yaw Direction

b）程序机动方案。

程序机动方案为：共进行2次程序机动，具体如下：

1）第1次程序机动。

第一次程序机动采用偏航方向正弦半周期机动方案，偏航程序角指令生成公式为

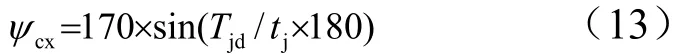
机动起始时刻（计时零点为三级关机）取350 s，机动时间取100 s。

2）第2次程序机动。

第2次程序机动采用偏航方向正弦半周期机动方案，偏航程序角指令生成公式为

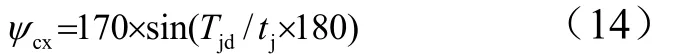
机动起始时刻（计时零点为三级关机）取800 s，机动时间取90 s。

c）交汇段躲避机动方案。

躲避机动起始时刻（计时零点为三级关机）取1170 s，躲避机动最优方向的俯仰程序角为-28°，俯仰程序角为-36°，机动时间取3 s。

d）弹道回归机动方案。

弹道机动回归起始时刻（计时零点为三级关机）取1200 s，弹道回归机动时间取32 s，弹道回归机动方向采用闭路制导方法得到。

5.2 弹道规划仿真结果

三级关机后进行机动规划的落点轨迹如图6所示，由图6可知，该方案实现了成功突防，准备命中目标的目的。

图6 弹道规划落点轨迹Fig.6 Tracks of the Descent Point Corresponding to the Trajectory Planning

6 结束语

本文以能实现轴对称再入飞行器中段机动飞行，提高生存概率为目的，构建了躲避机动级程序机动的约束模型，提出了轴对称再入飞行器飞行中段主动程序机动、交汇段躲避机动以及弹道回归的机动规划策略，并对其进行了仿真验证。本文的研究结果对提高再入飞行器机动变轨效能以及生存概率具有较好的参考价值，后续可深入开展俯仰及偏航方向多次多模式组合程序机动策略研究，以进一步提高突防效能。