特殊内凹形蜂窝结构等效扭转刚度研究
郭瑜超,王立凯,聂小华,吴存利
(中国飞机强度研究所,西安,710065)
0 引 言
蜂窝夹层结构具有较高的比刚度和比强度,同时具有良好的隔热、隔振特性,已经被广泛应用于航空、航天等领域,国内外学者对此开展了广泛研究[1~3]。但随着变体飞机等新型飞行器的出现,其要求机翼蒙皮具有良好的面内变形能力和较高的面外刚度,传统的正六边形蜂窝夹层结构无法满足此要求,因此对具有大柔性、大变形等特殊性能的结构材料,如各类具有零泊松比、负泊松比效应的蜂窝结构进行广泛的研究。
20世纪80年代,Gibson等[4]和Ashby便提出了负泊松比蜂窝构型——内凹六边形蜂窝,并对其力学性能进行预测;Theocaris等[5]针对一种星型的负泊松比蜂窝结构,详细讨论了其等效弹性模量的计算方法及弹性模量与蜂窝几何参数的关系;Prall等[6]针对一种手性负泊松比蜂窝结构,研究了其面内等效弹性模量及泊松比;董文俊等[7]研究了具有零泊松比效应的手风琴式蜂窝材料的等效模量和等效泊松比的计算方法进行了研究,采用经典欧拉梁理论,得到面内两个正交等效模量以及泊松比解析表达式,并对其进行了详细讨论;高珂等[8]针对此手风琴式蜂窝结构对其等效弯曲和扭转刚度进行了研究,得到等效弯曲刚度和扭转刚度的理论表达式,并利用数值方法验证了其正确性。
Bezazi等[9,10]提出一种特殊的内凹形蜂窝结构,并基于Timoshenko梁理论,对其面内等效弹性参数和进行了初步研究,同时初步讨论了该蜂窝结构的等效传热特性。文献[11]进一步利用虚功原理和能量法对该内凹形蜂窝结构的面内等效泊松比进行研究,发现其等效泊松比会随着其胞壁长度及角度的变化产生较大的改变,具有较好的应用前景;文献[12]将此内凹形蜂窝结构其简化为正交异性薄板,利用能量等效原理得到蜂窝结构等效弯曲刚度的解析表达式。综上所述,针对此内凹形蜂窝结构的面内等效弹性模量、泊松比、等效弯曲刚度已进行了广泛研究,但对其扭转刚度66D还没有明确给出理论表达式,本文将重点针对此型蜂窝结构的等效扭转刚度进行研究。
本文针对内凹形蜂窝结构,将其等效成正交异性薄板,利用薄板的变形能等效原理,推导出此型蜂窝结构等效扭转刚度的理论表达式,并详细讨论了等效扭转刚度与胞元几何尺寸的关系,最后利用有限元数值方法对理论公式的正确性进行了验证。
1 蜂窝等效扭转刚度理论推导
1.1 薄板变形能
内凹形蜂窝结构如图1所示。
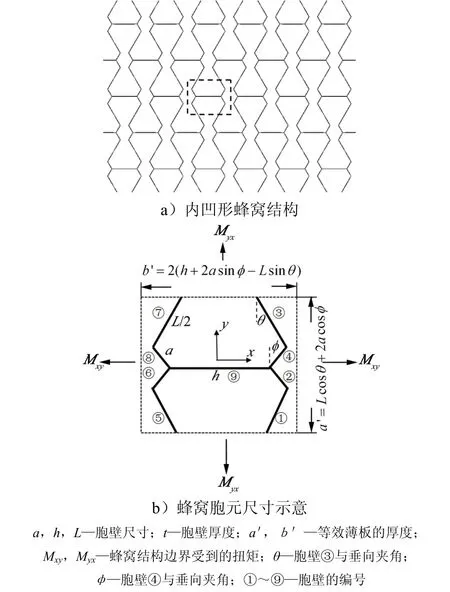
图1 蜂窝结构及胞元示意Fig.1 Honeycomb And Typical Cell
在计算该蜂窝结构(图1a所示)的等效扭转刚度时,为了简化计算过程,需要首先选取适当的蜂窝胞元,本文选取的典型胞元如图1b所示,胞元各个胞壁的尺寸及胞壁的编号在图1b中有明确标示。将胞元结构等效成为正交各项异性薄板,然后利用薄板的变形能公式可以得到其变形能。正交各项异性平板的变形能为[8]
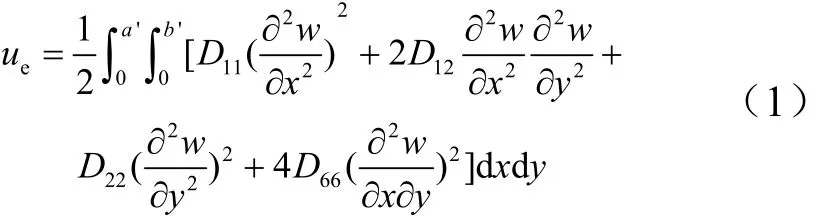
式中11D ,12D ,22D 为等效薄板的弯曲刚度系数;66D为等效薄板的扭转刚度系数;a',b'为等效薄板的边长。
薄板在受到均布扭矩而产生扭转变形时,薄板内任意一点的挠度可以表示为[13]
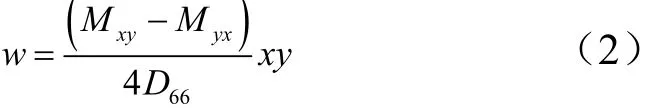
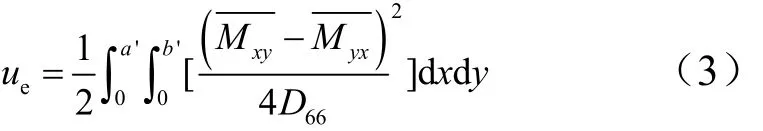
1.2 蜂窝胞壁变形能
计算蜂窝胞元各个胞壁的变形能之和,首先需要分别计算各个胞壁的变形能,在计算时需要将蜂窝胞元的胞壁等效为匀质平板,如图2所示。
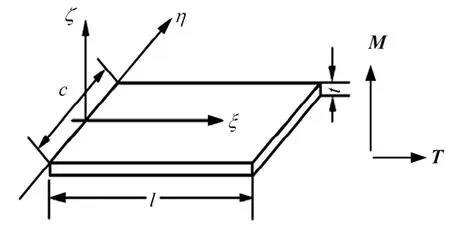
图2 蜂窝胞元壁板局部坐标系示意Fig.2 Local Coordinate System of Cell Wall c—胞壁高度;l—胞壁长度; t—胞壁厚度
由图2可知,弯矩M引起的蜂窝胞壁端面绕ζ轴的转角θM以及T引起的壁板端面绕ξ轴的扭转角θT(胞元壁板为非自由扭转)可通过式(4)求得[13]:

式中sE为蜂窝胞元材料的弹性模量;qτ为壁板的扭转系数,其值只与壁板的尺寸和材料的泊松比sν有关,见表1[13]的关系。

表1 壁板扭转系数与壁板尺寸及材料关系Tab.1 Relationship between Torsion Coefficient and Size&Material Of Wall
单个胞元壁板的变形能可以表示为

整个蜂窝胞元各个胞壁的变形能之和可以表示为

由于蜂窝结构的对称性,可以取一半胞元结构进行计算,如图3所示。
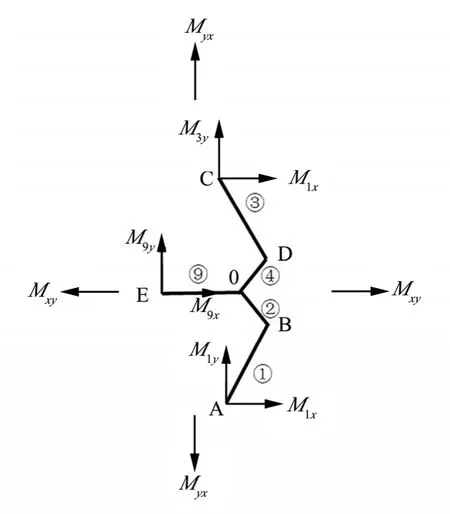
图3 胞壁受到的扭矩示意Fig.3 Torque Moment Acting on Each Cell Wall
由图3受力分析可以得到胞壁受到的弯矩和扭矩:


根据力矩的平衡关系,可以得到蜂窝胞元各个胞壁受到的弯矩和扭矩:

将式(7)、式(8)代入式(4)可以得到各个胞壁的弯曲及扭转变形,即:

为简化推导过程,假设均布扭矩Myx= 0 ,并将式(8)、式(9)代入式(5)可得蜂窝胞元各个胞壁的变形能为

利用蜂窝胞元的对称性,将式(10)代入式(6)可得蜂窝胞元各个胞壁的变形能之和,即:
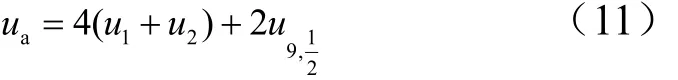
1.3 蜂窝结构等效扭转刚度
通过前面的计算分别得到等效薄板的变形能计算公式及蜂窝胞壁的变形能计算公式,利用变形能相等原理可计算蜂窝结构等效扭转刚度,变形能等效公式如下:

2 蜂窝等效扭转刚度数值计算
为验证理论分析结果的正确性,使用有限元方法进行数值验证,蜂窝结构的有限元建模分析借助航空结构分析软件HAJIF实现。
假设内凹形蜂窝结构的材料为铝合金,材料弹性模量sE=71 000 MPa,泊松比s0.3ν=,选择的胞元结构尺寸为:胞壁的长斜边长度l=5 mm,胞壁的短斜边长度a=1.667 mm,胞壁的横边长度h=5 mm,胞壁高度c=2.08 mm,胞壁夹角θ、ϕ不断变化。
蜂窝结构的细节有限元模型主要使用 QUAD4单元建立,综合考虑有限元模型的精度和效率,模型共包含 29×17个蜂窝胞元,模型包含有限元节点23 829个,单元16 320个。蜂窝结构的约束条件为:中心点约束6个方向的自由度。蜂窝结构载荷边界条件为:四边施加均布扭矩载荷,其中AB、CD两边施加总载为15 N·mm的均布扭矩,AD、BC两边施加总载为4.5 N·mm的均布扭矩。最终建立的蜂窝结构细节有限元分析模型如图 4所示,然后进行线性静力分析,得到蜂窝结构的变形。首先确定结构中的一个特征点E(E点在图4所示坐标系中的坐标为(50.0,43.3,0.0),通过计算得到图4蜂窝结构中E点沿z轴的变形w,然后将挠度代入式(14)可以反推蜂窝结构的等效扭转刚度[13]:

图4 蜂窝结构有限元模型示意Fig.4 Fem Model of Honeycomb Structure

式中 w为E点沿z轴的变形;x,y分别为A点的x坐标和y坐标。
3 计算结果讨论
蜂窝材料及胞元尺寸的选择见第 2节,在这些假设的前提下对蜂窝结构的等效扭转刚度进行讨论,讨论包括扭转刚度理论分析结果与数值计算结果。
图 5描述了当胞壁长度 L=5 mm、h=5 mm、a=1.667 mm,胞壁高度c=2.08 mm,胞壁夹角ϕ=30°、θ在 0°~90°之间变化时,夹角 θ变化对蜂窝等效扭转刚度的影响,同时讨论了蜂窝胞壁厚度t的变化对蜂窝等效扭转刚度的影响。由图5可知,当0°≤θ≤70°时,随着胞壁夹角 θ的增大,蜂窝结构等效扭转刚度逐渐减小;当70°≤θ≤90°时,蜂窝结构的等效扭转刚度随着夹角θ的增大而增大;当蜂窝胞壁厚度分别为t=0.0625 mm、0.09375 mm和0.125 mm时的蜂窝结构等效扭转刚度,对比结果显示,随着胞壁厚度t的增大,蜂窝结构等效扭转刚度明显提升。

图5 蜂窝结构等效扭转刚度与胞壁夹角θ的关系Fig.5 Relationship of Torsional Stiffness and Angle θ
图 6描述了当胞壁长度 L=5 mm、h=5 mm、a=1.667 mm,胞壁高度c=2.08 mm,胞壁夹角θ=30°,胞壁夹角φ在 0°~90°之间变化时,夹角φ变化对蜂窝等效扭转刚度的影响,同时讨论了蜂窝胞壁厚度 t的变化对蜂窝等效扭转刚度的影响。由图6可知,0°≤φ≤90°时,随着胞壁夹角φ的增大,蜂窝结构等效扭转刚度逐渐增大;当蜂窝胞壁厚度为t=0.0625 mm、0.09375 mm和0.125 mm时的蜂窝结构等效扭转刚度,对比结果显示,随着胞壁厚度t的增大,蜂窝结构等效扭转刚度明显提升。

图6 蜂窝结构等效扭转刚度与胞壁夹角φ的关系曲线Fig.6 Relationship of the Torsional Stiffness and Angle φ
图5 、图6中还对蜂窝结构等效扭转刚度的理论分析结果与有限元反推的结果进行了对比,对比结果显示理论结果与数值结果在趋势上基本一致,数值误差在 3%左右,说明在保证胞元壁板高度与长度比值在表1中的扭转系数的适用范围内的情况下,本文使用的理论分析方法是正确的。
4 结 论
针对一种特殊的内凹形蜂窝结构,将其等效为正交异性薄板,选择单个胞元结构,分别计算正交异性薄板的变形能以及胞元各个胞壁变形能之和,利用能量等效原理推导了该蜂窝结构等效扭转刚度的解析表达式,并展开了详细讨论,得到如下结论:
a)当胞壁长度、高度不变,胞壁夹角φ=30°、当0°≤θ≤70°时,随着胞壁夹角θ的增大,蜂窝结构等效扭转刚度逐渐减小;当70°≤θ≤90°时,蜂窝结构的等效扭转刚度随着夹角θ的增大而增大。
b)当胞壁长度、高度不变,胞壁夹角θ=30°、当0°≤φ≤90°时,随着胞壁夹角φ的增大,蜂窝结构等效扭转刚度逐渐增大。
c)随着胞壁厚度t的增大,蜂窝结构等效扭转刚度明显提升。
文中还对蜂窝结构的细节有限元模型进行了数值分析,并利用数值分析结果反推蜂窝结构的等效扭转刚度,得到的结果与理论分析结果基本一致,证明了本文理论方法的正确性,理论分析方法对该型蜂窝结构的工程应用有一定的指导意义。

